Nosso universo é infinito?
Atenção! Neste artigo, apenas uma teoria será expressa, sem evidência científica.
Bom dia Giktayms! Fui pressionado a escrever este artigo por um vídeo do YouTube sobre paradoxos numéricos incomuns. Ou seja, os paradoxos de
Zenão e por que é impossível dividir por zero, o que será discutido hoje.
O paradoxo de Zenão é facilmente explicado com base em
Aquiles e na tartaruga. Aqueles que não estão familiarizados com esse paradoxo, aqui está um vídeo visual de outro autor:
Eu recomendo que você leia antes de ler mais. (Paradoxo de Aquiles e tartarugas)
(Paradoxo de Aquiles e tartarugas)Se você não quiser assistir ao vídeo, vou lhe dizer brevemente: imagine que Aquiles está correndo atrás de uma tartaruga que o ultrapassa. A distância entre eles está diminuindo constantemente, pois Aquiles corre mais rápido que uma tartaruga. Como resultado, quando Aquiles se aproxima de uma distância de 1 metro, depois de um tempo será igual a
0,1 metro, depois
0,01, e assim por diante até o infinito. Isso significa que Aquiles nunca alcançará a tartaruga, mas na realidade tudo está completamente errado.
Na realidade, não há problema: pegamos Aquiles e a tartaruga, colocamos em uma esteira e, por favor, Aquiles ultrapassa calmamente a tartaruga. É precisamente nisso que reside a prova possível de que o universo não é infinito.
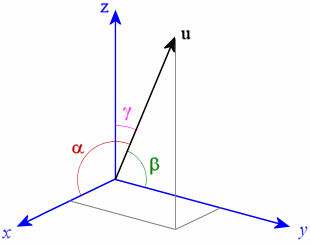 (Vetor no espaço 3D)
(Vetor no espaço 3D)Vamos tentar explicar isso no princípio dos jogos de computador. Normalmente, a posição de um objeto é escrita como um vetor que consiste nos eixos x, ye z. E cada valor é armazenado no tipo de dado
float (valor do ponto flutuante) . Por exemplo, o
Unity3D usa um flutuador de 32 bits para indicar sua posição no espaço. O valor mínimo dos quais:
1.175494351 E - 38. , que fornece um movimento suave em quase todas as escalas. Aqui a palavra importante é
"quase" , isto é, se reduzirmos e aproximarmos bastante o modelo, veremos como ele se move em saltos. Saltando de
0, ... 1 para
0, ... 2 para
0, ... 3 , etc. Isso significa que, na simulação, em qualquer cenário, Aquiles ultrapassará a tartaruga. Mas como eles dizem que não há mal sem o bem. Se tivermos um valor mínimo de flutuação, haverá uma borda máxima, por assim dizer, do espaço
3D . Vá além do que não seremos permitidos
(vamos chamá-lo) as leis da física do mundo virtual. Na realidade, simplesmente não podemos dar mais do que o valor máximo de uma variável.
Se voltarmos ao paradoxo de Zenão, Aquiles não apenas nunca alcançará a tartaruga, como também nunca alcançará a fronteira de seu mundo de fantasia, pois ele será infinito. De -∞ a + ∞, curiosamente, obtemos a mesma função
f (x) = 1 / x . E o mais engraçado é que o valor
x / 0 não se enquadra nessa função, pois a função nunca chegará a zero, como a tartaruga de Aquiles.
(Na verdade, isso não pode ser dividido por zero)Teoria suficiente, vamos praticar. Pegue o mundo real, todos somos constituídos por átomos, os átomos são constituídos por prótons e elétrons de nêutrons, que por sua vez são constituídos por quarks
(partículas elementares) . Tanto na simulação quanto no mundo real, Aquiles não precisa ultrapassar uma tartaruga. Tudo isso leva ao fato de que, tanto na simulação quanto na realidade, as partículas elementares também devem saltar pelos números
0, ... 1 0, ... 2 0, ... 3 como acontece no jogo, porque Aquiles pode ultrapassar tartaruga aqui e ali. Isso nos diz que o paradoxo de Zenão funciona apenas no papel ou em seu sistema de coordenadas, cujo valor é de -∞ a + ∞. Na realidade, saltando nos menores valores, as partículas elementares de Aquiles em algum momento ultrapassam a tartaruga, suas coordenadas se tornam iguais, após o que Aquiles avança.
Então, aprendemos qual sistema de coordenadas nosso espaço usa, vamos voltar ao tópico principal. Se tivermos um valor mínimo, haverá um máximo - a
borda do nosso universo . Há quem diga por que, então, por um lado, pode ser infinito e, por outro, finito. Mas o problema é que as coordenadas ou a posição são apenas um elemento de um grande sistema chamado espaço, e podem ser completamente infinitas ou completamente finitas. Além disso, tudo isso levanta a questão, e por acaso não estamos em uma simulação de computador, não é? Mas este é um tópico para outro artigo.
Sumário
Então, hoje chegamos à conclusão de que o universo
NÃO é infinito. Neste post, apenas a teoria foi expressa como ninguém realmente conhece o universo, e não pode prová-lo. Mas talvez com este artigo, eu forcei alguém a fazer novas descobertas.
Fonte