As equações de Navier-Stokes descrevem fenômenos cotidianos simples, como a água que flui de uma mangueira de jardim - no entanto, são baseados em um problema cuja solução foi estimada em um milhão de dólares

Na física, existem equações que descrevem tudo, desde o alongamento do espaço-tempo até o vôo de um fóton. No entanto, apenas um conjunto de equações é considerado tão matematicamente complexo que foi escolhido como um dos sete "
Problemas do Milênio ", pelos quais o
Instituto Clay de Matemática oferece um prêmio de um milhão de dólares: essas são
as equações de Navier-Stokes que descrevem o fluxo de fluidos.
Recentemente,
escrevi sobre como um novo resultado importante foi obtido para essas equações. E este trabalho indica que o progresso em direção ao Prêmio do Milênio será mais difícil do que o esperado. Por que essas equações descrevem fenômenos familiares como a água que flui através de uma mangueira matematicamente mais difícil de entender do que, por exemplo, as equações de campo de Einstein, que incluem objetos impressionantes como buracos negros?
A resposta, como eu a entendo, está na turbulência. Todos nós experimentamos esse fenômeno, em vôo no ar não homogêneo a uma altitude de 10.000 m, ou quando observamos um funil da água deixando o ralo no banho. No entanto, o conhecimento não decorre da consciência: a turbulência é uma das áreas menos compreendidas do mundo físico.
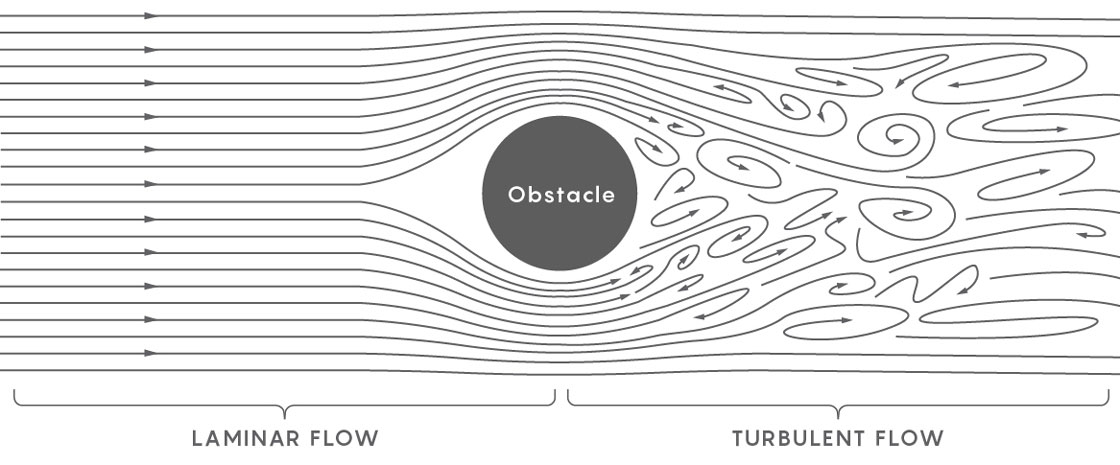
Um exemplo de fluxo sem turbulência é um rio calmo. Cada parte dela se move na mesma direção e na mesma velocidade. O fluido turbulento aparece quando o fluxo de um rio quebra, de modo que diferentes partes do fluxo começam a se mover em direções diferentes em velocidades diferentes. Os físicos descrevem a formação de turbulência a princípio como a aparência de um funil em um fluxo suave e, em seguida, como a formação de pequenos funis no primeiro funil e funis ainda menores nesses funis - um mar de funis que entra no líquido, de modo que o líquido se decompõe em partes discretas, cada uma das quais interage entre si e se move em sua própria direção.
Os pesquisadores querem entender exatamente como um fluxo suave se decompõe em turbulência turbulenta e modelar a forma futura do fluido após a turbulência ter cobrado seu preço. Mas o Desafio do Milênio é formulado de maneira mais modesta: você só precisa provar que sempre existem soluções. Ou seja, a questão é: as equações podem descrever qualquer fluido, com quaisquer condições iniciais e para um futuro infinitamente distante?
"O primeiro passo é simplesmente tentar provar que as equações têm algumas soluções", diz Charlie Fefferman, matemático da Universidade de Princeton. "Isso não dá uma compreensão real do comportamento dos líquidos, mas se você também não o tem, não sabe nada".
Então, como alguém pode provar a existência de soluções? Você precisa entender por que eles podem não estar. As equações de Navier-Stokes implicam o cálculo de mudanças em quantidades como velocidade e pressão. Os matemáticos estão preocupados com o seguinte cenário: você foge dessas equações e, após algum tempo finito, eles dizem que uma partícula fluida se move em velocidade infinita. E este é o problema - calcular a mudança no valor infinito não é mais fácil do que dividir por zero. Os matemáticos chamam essas situações de "explosão" e, no caso de uma explosão, as equações deixam de funcionar e nenhuma solução é encontrada.
 As equações de Navier-Stokes descrevem o fluxo de um fluido incompressível.
As equações de Navier-Stokes descrevem o fluxo de um fluido incompressível.
Em geral, o produto da massa (parte azul) e aceleração (violeta) é igual às forças que atuam no líquido (laranja):- ρ é a densidade do fluido;
- dV / dt - mudança de velocidade ao longo do tempo;
- V ∇V - velocidade e direção do movimento;
- ∇P - mudança de pressão interna;
- ρ g - a influência de forças externas (por exemplo, gravidade);
- μ 2 V - a influência de forças internas (viscosidade).
A prova da ausência de explosões (e a existência de soluções) é equivalente à prova de que a velocidade máxima de qualquer partícula líquida permanece limitada por algum valor finito. Uma das quantidades mais importantes é a energia cinética do líquido.
Quando você começa a simular o fluxo usando as equações de Navier-Stokes, seu fluido possui uma quantidade inicial de energia. Em fluxos turbulentos, a energia pode começar a se concentrar. Em vez de se espalhar uniformemente pelo rio, a energia cinética pode ser coletada em banheiras de hidromassagem de tamanho arbitrariamente pequeno, e as partículas nessas banheiras de hidromassagem (teoricamente) podem acelerar a velocidade infinita.
“Com a transição para escalas cada vez menores, a energia cinética se torna cada vez menos útil para o controle de decisões. A decisão pode fazer qualquer coisa, e eu não saberei controlá-la ”, diz Vlad Vikol, matemático da Universidade de Princeton que escreveu um novo trabalho com Tristan Buckmaster.
Os matemáticos classificam equações parcialmente diferenciais com base na extensão em que eles podem começar a se comportar mal em escalas infinitamente pequenas. As equações de Navier-Stokes estão no extremo desta escala. A complexidade da matemática das equações, em certo sentido, reflete a complexidade dos fluxos turbulentos que eles devem ser capazes de descrever.
"Quando você aumenta o zoom em algum lugar e, do ponto de vista matemático, perde informações sobre a solução", diz Vikol. "Mas a turbulência deve descrever exatamente isso - a transferência de energia cinética de escalas grandes para cada vez menores, por isso realmente exige que você aumente a escala."

Falando sobre as propriedades matemáticas das equações físicas, é natural fazer uma pergunta: esses argumentos mudarão a maneira como encaramos o mundo físico? No caso das equações de Navier-Stokes e do Problema do Milênio, a resposta será "sim" e "não". Após quase 200 anos de experimentação, fica claro que as equações funcionam: o fluxo previsto por Navier-Stokes coincide consecutivamente com o fluxo observado nos experimentos. Se você é um físico que trabalha em um laboratório, isso pode ser suficiente para você. Mas os matemáticos precisam saber mais - eles querem verificar se é possível seguir essas equações até o fim para monitorar como exatamente o fluxo muda de um momento no tempo para outro (para qualquer configuração inicial de fluido) e até para capturar a fonte de turbulência.
"O comportamento dos líquidos é cheio de surpresas", diz Fefferman. "Essas surpresas são, em princípio, explicadas pelas equações fundamentais que controlam o fluxo de fluidos, mas como passar das equações que controlam o movimento de um fluido para uma descrição de como o fluido realmente se move é um mistério".