Dois matemáticos provaram que, sob certas condições extremas, as equações de Navier-Stokes dão um absurdo
As equações de Navier-Stokes, com a ajuda de vários termos lacônicos, descrevem um dos fenômenos mais comuns do mundo físico: o fluxo de fluidos. Hoje, essas equações, que datam da década de 1820, são usadas para descrever tudo, desde correntes oceânicas e turbulência após um avião até o fluxo de sangue no coração.
Embora os físicos considerem essas equações confiáveis, como um martelo, os matemáticos desconfiam delas. Para um matemático, o fato de que essas equações parecem funcionar não significa muito. Eles precisam de prova de que as equações estão livres de erros: que, para qualquer previsão fluida e de longo prazo, distribuída no futuro, a matemática das equações não falhará. Não foi fácil encontrar essa garantia. A primeira pessoa ou equipe que puder provar que as equações de Navier-Stokes sempre funcionarão - ou fornecerá um exemplo que prova que elas não funcionam - poderá receber uma recompensa por resolver um dos
problemas do milênio , anunciado pelo
Instituto Matemático de Clay , e um milhão de dólares em Além disso [a partir de 2017, apenas uma das sete tarefas do milênio (hipótese de Poincaré) foi resolvida por Gregory Perelman / aprox. transl.].
Os matemáticos desenvolveram muitas maneiras de resolver esse problema. O novo trabalho, publicado em setembro, coloca sérias questões sobre se uma das abordagens mais populares para o problema, desenvolvida ao longo de muitos anos, pode ser bem-sucedida. O trabalho, escrito por Tristan Buckmaster e Vlad Vikol, da Universidade de Princeton, é o primeiro resultado que mostra como, sob certas condições, as equações de Navier-Stokes fornecem uma descrição contraditória do mundo físico.
"Estamos tentando entender certos problemas inerentes a essas equações e por que as pessoas provavelmente terão que repensá-las", diz Buckmaster.
O trabalho de Buckmaster e Wikol mostra que, se você fizer suposições muito grosseiras ao resolver as equações de Navier-Stokes, elas começam a não fazer sentido: dizem que o mesmo fluido com as mesmas condições iniciais pode ocorrer em dois ou mais estados diferentes. Pode fluir de uma maneira ou de uma maneira completamente diferente. Nesse caso, essas equações não podem descrever de maneira confiável o mundo físico para o qual foram desenvolvidas.
Equações explodindo
Para entender como as equações podem quebrar, imagine uma corrente oceânica. Dentro de sua estrutura, podem existir fluxos locais, como resultado de que algumas de suas partes podem se mover em uma direção e em uma velocidade, e outras em outra direção em outra velocidade. Os fluxos locais interagem entre si na constante ação mútua de atrito e pressão da água, que determina seu fluxo.
Os matemáticos modelam essa interação usando um mapa informando sobre as direções e taxas de fluxo em qualquer ponto do fluido. Esse mapa, chamado campo vetorial, é um instantâneo da dinâmica interna de um fluido. As equações de Navier-Stokes tiram essa foto e a reproduzem como um vídeo, dizendo exatamente como o campo vetorial ficará em cada momento subsequente no tempo.
O mapa do vento (windy.com) funciona de maneira semelhante a um campo vetorial. Em cada ponto, o vento tem uma certa direção e força.Essas equações funcionam. Eles descrevem o fluxo de fluido de maneira tão confiável quanto as equações de Newton prevêem as posições futuras dos planetas; os físicos os usam constantemente e coincidem constantemente com os resultados das experiências. No entanto, os matemáticos precisam de mais do que confirmação episódica - eles precisam de prova de que as equações não são violadas, de que, independentemente do campo vetorial em que você comece e até que ponto o reproduzirá no futuro, as equações sempre fornecerão a você campo de vetor novo e exclusivo.
Esse é o tema do Problema do Milênio, perguntando se as equações de Navier-Stokes têm soluções (a solução, de fato, é um campo vetorial) para todos os pontos de partida em todos os momentos. Essas soluções devem garantir a direção exata e a força do fluxo em cada ponto do fluido. As soluções que fornecem informações com uma resolução infinitamente pequena são chamadas de "suaves". Para uma solução suave, cada ponto do campo tem um vetor associado a ele, o que permite que você viaje "sem problemas" pelo campo, sem ficar preso nos pontos em que o vetor está ausente - em um ponto em que você não entenderá o movimento adicional.
Soluções suaves são uma representação completa do mundo físico, mas, do ponto de vista matemático, elas nem sempre existem. Os matemáticos que trabalham em equações como essas se preocupam com esta situação: você executa as equações de Navier-Stokes e observa as mudanças no campo vetorial. Após um tempo finito, as equações dizem que uma determinada partícula de fluido se move com velocidade infinita. Então você terá problemas. As equações incluem medir mudanças em propriedades como pressão, atrito e velocidade do fluido - falando no jargão, elas derivam essas quantidades - mas não é mais fácil derivar uma derivada de uma quantidade infinita do que dividir por zero. Portanto, se as equações derem um valor infinito, podemos dizer que elas recusaram você ou "explodiram". Eles não podem mais descrever os estados subsequentes do seu fluido.
Tal "explosão" é uma evidência de que as equações carecem de uma descrição de algumas propriedades do mundo físico que elas devem descrever. "Talvez as equações não abranjam todos os efeitos de um fluido real, porque em um fluido real não esperamos uma velocidade infinita de partículas", diz Buckmaster.
A solução para o problema do milênio é mostrar que as equações de Navier-Stokes nunca explodem ou encontrar as condições sob as quais isso acontece. Uma das estratégias usadas pelos matemáticos é suavizar os requisitos para a precisão com que essas equações devem descrever as soluções necessárias.
Perturbação do fluxo
As equações de Navier-Stokes devem descrever o fluxo de qualquer fluido, com quaisquer condições iniciais, e estender a descrição infinitamente para o futuro. Tentando provar essa habilidade, os matemáticos às vezes “enfraquecem”, ou seja, usam descrições aproximadas de campos vetoriais que descrevem um fluido. Mas há dificuldades com isso.
Idealmente, os matemáticos querem provar que a aplicação das equações de Navier-Stokes a qualquer fluido contínuo e “suave” produzirá um resultado único.
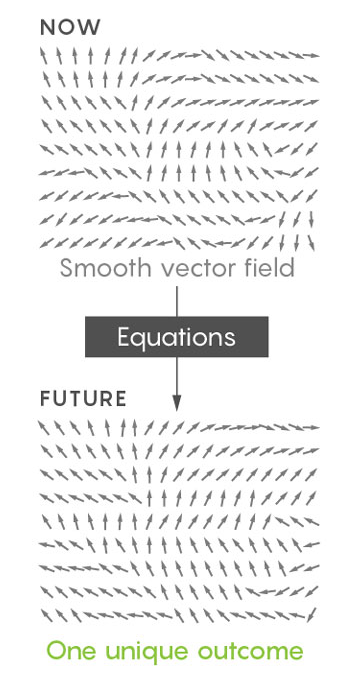
No entanto, é mais fácil trabalhar com campos vetoriais "fracos" e não tão detalhados. E os matemáticos descobriram que algumas descrições fracas produzem resultados não exclusivos - elas permitem que o mesmo fluido flua nas mesmas condições iniciais de duas maneiras.
De fraco a suave
Quando os matemáticos estudam equações como essas, às vezes começam a expandir a definição do que constitui uma solução. Soluções suaves exigem o máximo de informações - no caso da Navier-Stokes, elas exigem que em todo ponto do campo vetorial associado ao líquido exista um vetor. Mas e se relaxarmos os requisitos e dissermos que você precisa calcular vetores apenas para alguns pontos do campo ou obter apenas valores aproximados dos vetores? Tais decisões são chamadas de "fracas". Eles permitem que os matemáticos sintam o comportamento da equação sem o trabalho tedioso de encontrar absolutamente todas as soluções (o que na prática pode não ser possível).
Tristan Buckmaster, matemático da Universidade de Princeton"De algum ponto de vista, decisões fracas são ainda mais fáceis de descrever do que decisões reais, porque você precisa saber muito menos", disse Camillo De Lellis, co-autor de Lazlo Schekelikhidi, que escreveu várias obras importantes que lançaram as bases para o trabalho de Buckmaster e Vikola.
Soluções fracas vêm em diferentes graus. Se você imaginar uma solução suave na forma de uma imagem matemática de um líquido com resolução infinita, soluções fracas serão algo como as versões de 32 bits, 16 bits ou 8 bits desta imagem.
Em 1934, o matemático francês
Jean Leray definiu uma classe importante de soluções fracas. Em vez de trabalhar com vetores exatos, as "soluções Leray" assumem o valor médio dos vetores em uma pequena vizinhança do campo vetorial. Leray provou que você sempre pode resolver as equações de Navier-Stokes, permitindo que suas decisões tomem a forma desse tipo. Em outras palavras, as decisões de Lera não explodem.
A conquista de Lera determinou uma nova abordagem para o problema de Navier-Stokes: comece pelas soluções da Lera, cuja existência já é conhecida, e veja se elas podem ser transformadas em soluções suaves cuja existência você deseja provar. Esse processo se assemelha àquele em que você começa com uma imagem aproximada e vê se consegue gradualmente distorcer a resolução para obter a imagem perfeita da realidade.
"Uma das estratégias possíveis é mostrar que essas decisões fracas de Lera são tranqüilas e, se você puder demonstrar que são tranquilas, resolverá o Desafio do Milênio", disse Bakmaster.
Vlad Vkol representa metade da equipe que revelou problemas na abordagem para verificar as equações de Navier-Stokes.Há outro problema. As soluções das equações de Navier-Stokes correspondem a eventos físicos reais, e os eventos físicos ocorrem de uma maneira possível. Diante disso, gostaria que suas equações tivessem apenas um conjunto de soluções exclusivas. Se as equações fornecerem muitas soluções possíveis, elas não poderão fazer seu trabalho.
Portanto, os matemáticos poderão usar as soluções da Leray para resolver os problemas do milênio, apenas se as soluções da Leray forem únicas. As soluções não exclusivas de Lera significarão que, de acordo com as regras de Navier-Stokes, o mesmo fluido com as mesmas condições iniciais pode chegar a dois estados físicos diferentes, que não têm significado físico, e implica que as equações não descrevem realmente o que deveria.
O novo resultado do Bakmaster e da Wikol é a primeira dica de que, para certas definições de decisões fracas, isso pode acontecer.
Muitos mundos
Em seu novo trabalho, Buckmaster e Wikol consideram soluções ainda mais fracas que as soluções de Leray - soluções que usam o mesmo princípio de média que o de Leray, mas enfraquecem mais um requisito adicional (conhecido como desigualdade de energia). Eles usam o método de “integração convexa”, que se origina do trabalho sobre a geometria do matemático John Nash, e é posteriormente envolvido no estudo de líquidos por De Lellis e Schekelikhidi.
Usando essa abordagem, Buckmaster e Wikol provam que essas soluções muito fracas das equações de Navier-Stokes não são únicas. Eles, por exemplo, demonstram que, se você começar com um líquido completamente calmo, por exemplo, com um copo de água ao lado da cama, dois tipos de eventos serão possíveis. O primeiro é óbvio: a água começa com um estado calmo e sempre permanece calmo. O segundo é fantástico, mas matematicamente possível: a água começa em um estado calmo, explode no meio da noite e depois volta a um estado calmo.
"Isso prova a falta de exclusividade, porque pelo menos dois objetos podem ser construídos a partir dos dados iniciais", diz Vikol.
Buckmaster e Wikol provaram a existência de muitas soluções fracas não exclusivas (não apenas as duas descritas acima) das equações de Navier-Stokes. A importância dessas evidências continua a ser entendida. Em algum momento, soluções fracas podem se tornar tão fracas que deixam de estar relacionadas a soluções mais suaves que deveriam imitar. Nesse caso, o resultado obtido pela Bakmaster e pela Wikol levará a pouco.
“Esse resultado é claramente um aviso, mas pode-se argumentar que esse aviso diz respeito à idéia mais fraca de decisões fracas. Há muitas camadas de soluções mais fortes que você pode esperar para um comportamento muito melhor ”no caso das equações de Navier-Stokes”, diz De Lellis.
Backmaster e Wikol também pensam em termos de camadas, e ele se concentra nas decisões de Lehr - em provar que elas também permitem múltiplas físicas, nas quais o mesmo fluido do mesmo estado pode ter diferentes formas no futuro.
"Tristan e eu acreditamos que as decisões de Leray não são únicas. Ainda não provamos isso, mas nosso trabalho cria a ponte para um ataque a essa tarefa ”, afirmou Vikol.