Passagem de Vênus no disco do Sol e determinação da distância entre eles

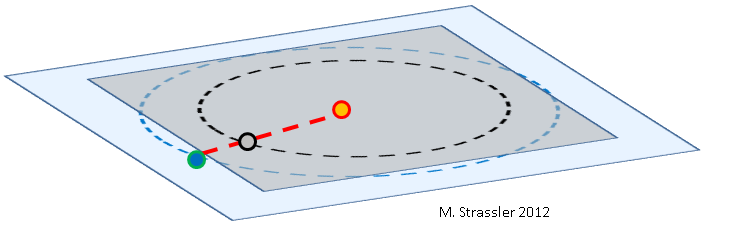
Fig. 1: Terra (azul), Vênus (cinza) e Sol (laranja), sem escala.

Em relação à passagem de Vênus através do disco do Sol em 2012, muitos artigos já foram escritos. Sobre quão raramente esse evento acontece, e por que exatamente: em teoria, Vênus, movendo-se ao redor do Sol com mais frequência do que a Terra, deve passar entre a Terra e o Sol durante cada uma de suas voltas (Fig. 1), mas porque Como as órbitas de dois planetas não estão alinhadas (elas não estão no mesmo plano, veja a Fig. 2), Vênus geralmente passa acima ou abaixo do Sol do ponto de vista da Terra.

Mas, em vez de repetir as palavras de outras pessoas, quero adicionar alguns detalhes que não são tão fáceis de encontrar na Internet.

Você pode ter lido que, usando uma técnica baseada no raciocínio do astrônomo Edmund Halley (o famoso cometa Halley) feito por ele de 1678 a 1716, assim como James Gregory, a passagem de Vênus em 1716 foi usada para determinar a distância da Terra a O Sol (e antes de Vênus e todos os outros planetas) com um erro de 2% é o mais alto dos alcançados naquele momento. Esperava-se que a precisão fosse 10 vezes maior, mas um efeito óptico inesperado chamado “ efeito gota preta ” interveio no processo - ainda há debates sobre os motivos exatos para sua ocorrência. Mas você pode não ter lido que essa medida - e muitas outras medidas de distâncias em astronomia, até estrelas razoavelmente próximas - é baseada no princípio da paralaxe , no mesmo fato geométrico que nossos olhos e cérebro usam para perceber a profundidade ou nossa capacidade de sentir quão longe os objetos estão de nós simplesmente olhando para eles.


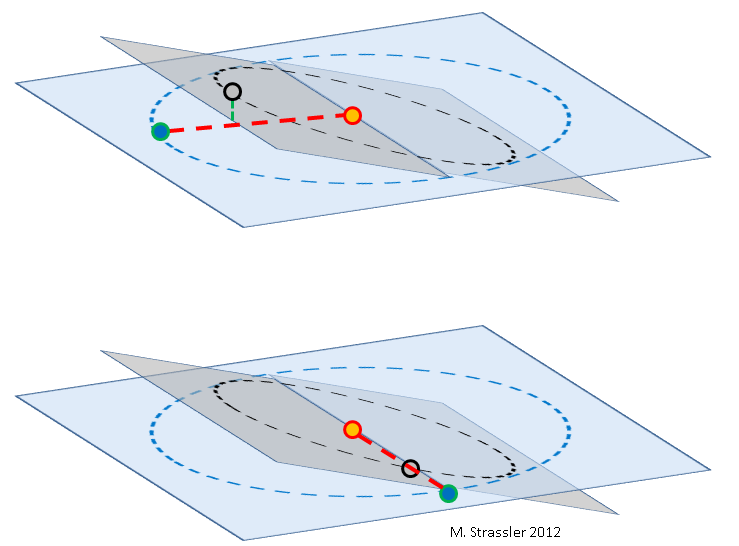Fig. 2: Terra (azul), Vênus (cinza) e Sol (laranja), sem escala. A órbita de Vênus (um círculo preto em um retângulo cinza) é inclinada em relação à órbita da Terra (um círculo azul em um retângulo azul). O grau de inclinação é muito exagerado. Como a Terra e Vênus giram em torno do Sol em velocidades diferentes, eles podem se cruzar em qualquer ponto das órbitas.

Acima: durante essa passagem, Vênus está localizado acima ou abaixo (linha verde) da linha que liga a Terra e o Sol (linha vermelha), de modo que Vênus não passa pelo disco solar.

Abaixo: Em casos raros, a linha que liga a Terra e o Sol coincide com a linha de interseção dos planos das órbitas, e Vênus está perto da mesma linha, o que leva à passagem.

Sem paralaxe, também é fácil determinar a distância relativa de Vênus ao Sol - isto é, a razão entre o raio da órbita de Vênus _LV e o raio da órbita da Terra L _E. Portanto, na astronomia do Renascimento, as distâncias relativas dos planetas à Terra e ao Sol foram calculadas muito cedo. Mas, para determinar _LV e _LE separadamente, é necessário medir a paralaxe, e a passagem de Vênus pode fornecê-la. A passagem de Vênus na década de 1760 deu uma medida bastante precisa de _LE - _V , a distância "absoluta" da Terra a Vênus; isso tornou possível descobrir _LE , _LV e as distâncias para todos os outros planetas com um erro de alguns por cento. Antes disso, no final do século XVII, era feita uma medição da distância da Terra a Marte, que apresentava um erro de cerca de 10%; também foi baseado em paralaxe, mas essa é uma história completamente diferente.

Observação preliminar: a Terra e Vênus e até o Sol são muito pequenos em comparação com as distâncias entre eles, por isso é quase impossível desenhar imagens precisas. Nas ilustrações, você sempre precisa desenhar planetas maiores do que realmente são, em relação às distâncias entre eles, apenas para entender o conceito. Tenha isso em mente! Todas as minhas ilustrações não são desenhadas em escala.

Os tamanhos relativos das órbitas de Vênus e da Terra

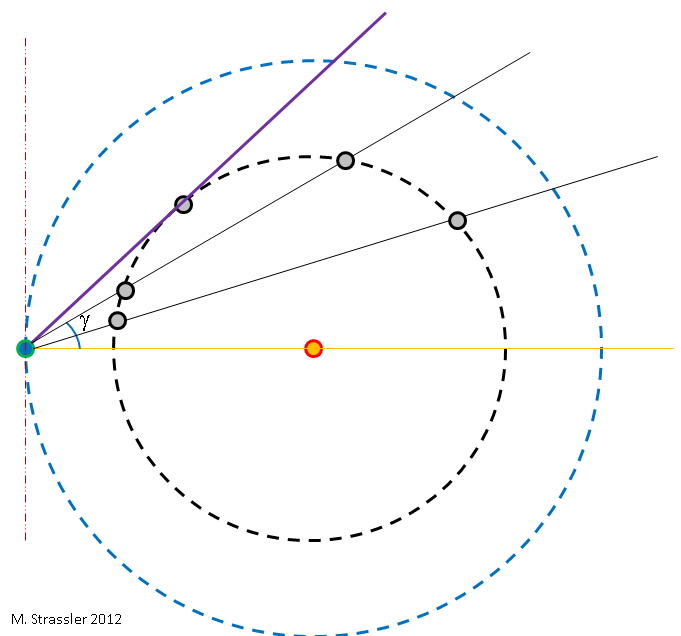Fig. 3

Para entender a principal razão da simplicidade da determinação de _LV / _LE , suponha que as órbitas da Terra e Vênus sejam circulares e alinhadas - elas estão no mesmo plano (como mostrado na Figura 1, isométrico, e na Figura 3 é uma "vista superior"). De fato, as órbitas da Terra e Vênus são ligeiramente alongadas e não alinhadas (Fig. 2). Mas a elipticidade e a incompatibilidade de planos não são muito importantes para o nosso raciocínio; portanto, primeiro podemos ignorá-los e depois lembrar novamente para obter respostas mais precisas.

Aqui aplicaremos a tecnologia clássica da física: faremos uma aproximação suficiente para a tarefa atual e não iremos mais fundo do que o necessário. Essa é uma maneira muito poderosa de pensar sobre ciência e conhecimento em geral - basta responder a qualquer pergunta com um certo nível de precisão, para que você possa usar a técnica mais simples daquelas que fornecerão o nível de precisão desejado. Este método tem sido perfeitamente utilizado há séculos e é aplicável não apenas à física.

Portanto, tomaremos a aproximação na qual as órbitas são circulares e alinhadas e receberemos aproximadamente as respostas corretas, com um erro de alguns por cento. Isso será suficiente para demonstrar os conceitos básicos que eu procuro. Acredite, você pode fazer cálculos muito mais precisos - ou pode se tornar um especialista nesse assunto. Mas nossa aproximação não apenas fornecerá uma resposta muito boa, mas também será capaz de mostrar por que é tão fácil calcular a razão de _LV para _LE , mas não os valores de _LV e LE.

Durante o ano em que a Terra e Vênus giram em torno do Sol em velocidades diferentes, a posição relativa da Terra e Vênus em relação ao Sol muda. Se, em um determinado dia (dia, mês, ano), decido fazer um desenho com o Sol no centro e a Terra à esquerda, como na Fig. 2, então Vênus pode estar em qualquer lugar em sua órbita. Isso significa que, do ponto de vista da Terra, o ângulo entre Vênus e o Sol no céu mudará dependendo da data. Isso é mostrado na fig. 3, onde o ângulo é chamado γ. O ângulo é fácil de medir; encontre Vênus no céu após o pôr do sol ou antes do nascer do sol e meça o ângulo entre Vênus e o Sol; ver foto 4)


Fig. 4

A partir da fig. A Figura 3 mostra que γ tem um tamanho máximo - o ângulo entre as linhas laranja e roxa. Movendo-se em órbita, Vênus aparecerá em outro lugar a cada pôr do sol; por algum tempo, ele subirá mais acima do horizonte por várias noites seguidas e gradualmente começará a aparecer abaixo. Observando Vênus por várias noites seguidas e medindo γ, podemos determinar o valor máximo de γ, que chamarei de γ _máx .

A partir da fig. 3 é óbvio que (como mostrado na Fig. 4) γ _{max é} inferior a 90 °, uma vez que a linha violeta deve ficar entre o laranja e o vermelho, perpendicular. Geometricamente, isso é uma conseqüência do fato de Vênus estar sempre mais perto do Sol do que da Terra. Esses ângulos explicam por que Vênus sempre é visível imediatamente após o pôr do sol ou antes do amanhecer (exceto nos dias em que está localizado atrás do Sol). Vênus não pode estar no auge após o anoitecer, porque para isso ela teria que estar à esquerda da linha vermelha.


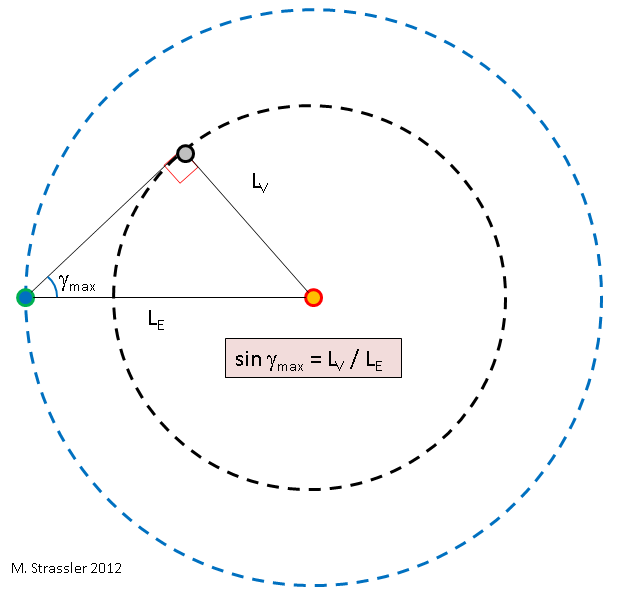Fig. 5

Agora podemos determinar a razão dos raios de duas órbitas - L _V para L _E - usando γ _max . Esta é a geometria mais simples, veja a fig. 5. A conclusão é que, quando Vênus está no ângulo máximo do Sol, a linha entre o Sol e Vênus é perpendicular à linha entre a Terra e Vênus, de modo que as linhas que conectam esses três objetos formam um triângulo retângulo. A partir daqui, começamos a usar a trigonometria padrão:

$$

$$L_V / L_E = \ gamma_ {max}$$

E a partir daqui, com a ajuda de outras fórmulas geométricas simples, obtemos a relação entre as distâncias para outros planetas.

Isso não é totalmente exato, pelas razões indicadas no início; as órbitas dos planetas são elipses e não ficam no plano aquático. Em outras palavras, L _V e L _E não _são armazenadas durante o ano, e γ _max é aplicado um pouco mais complicado, em três dimensões, como na Fig. 2, mas não em dois, como na Fig. 1, 3 e 5. Mas com a ajuda de medições precisas da posição de Vênus e do Sol no céu, é possível determinar as órbitas exatas de Vênus e da Terra ao redor do Sol e melhorar os cálculos. O significado é o mesmo; todas as medidas da posição de Vênus e do Sol no céu nos permitem apenas medir os tamanhos relativos das órbitas de Vênus e da Terra. Mas os valores exatos de _LV e LE não podem ser determinados dessa maneira. Aqui precisamos de uma abordagem diferente.

Passagem de Vênus, paralaxe e distância ao Sol

A razão pela qual a passagem de Vênus permite medir os valores absolutos das órbitas da Terra e Vênus é que esse processo pode ser observado com alta precisão em diferentes lugares do globo, como resultado, você terá duas perspectivas da localização visível de Vênus em relação ao Sol, medida em diferentes locais com conhecimento conhecido. distância entre eles. Medir a paralaxe permite determinar o valor absoluto da distância da Terra a Vênus a partir do ângulo de paralaxe e a distância entre dois pontos de medição na Terra - assim como um tipo de objeto diferente para os olhos esquerdo e direito, permite que o cérebro nos dê uma sensação de profundidade - uma sensação de distância dos objetos.


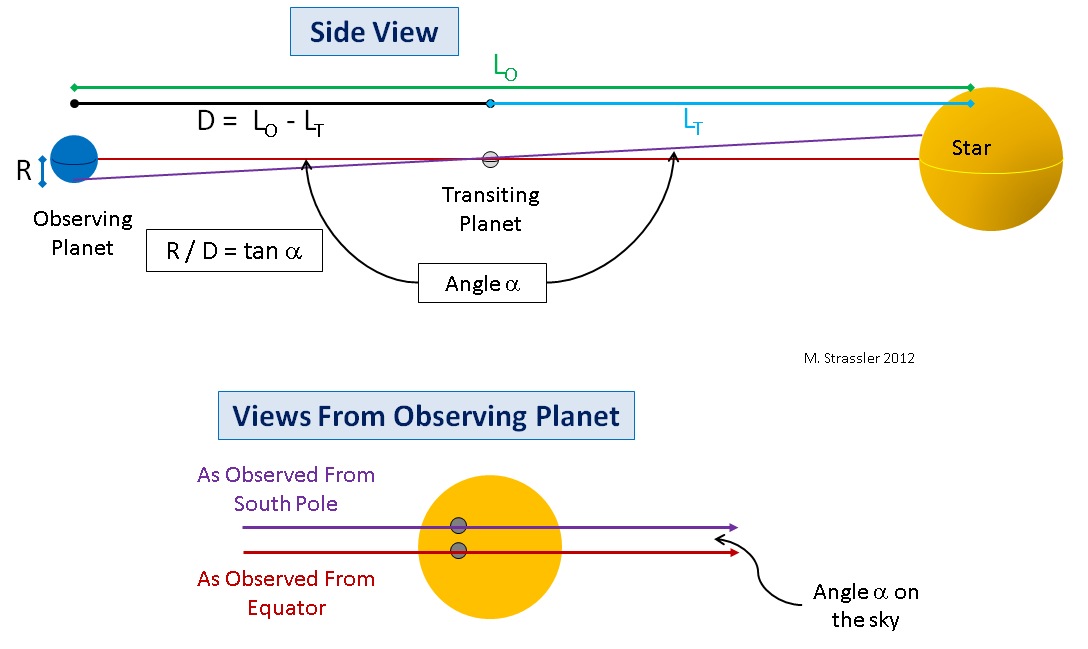Fig. 6

Para uma demonstração, deixe-me desenhar como será a aparência de um grande planeta. Na fig. A Figura 6 mostra o planeta com o qual observaremos a passagem (será a Terra) e o planeta passando na frente da estrela (será Vênus). Apresentarei uma situação simplificada (apenas para simplificar a geometria e o conceito principal), em que os planetas e a estrela estão alinhados; portanto, do ponto de vista do observador no equador, um planeta passante passará ao longo do equador da estrela. Acima na fig. 6 mostra uma vista lateral; observe a linha vermelha do equador do planeta observador até a estrela através do equador do planeta passando pelo disco da estrela.

No caso de alinhamento perfeito, o observador no equador do planeta exterior verá como o planeta interior passa ao longo do equador da estrela. Isto é mostrado como uma linha vermelha na parte inferior da fig. 6. Mas o observador do polo sul do planeta exterior verá como o planeta interior passa a estrela ao longo do caminho (linha roxa) ao norte do equador da estrela (no caso do polo norte, tudo será vice-versa). Se medirmos o ângulo α no céu entre os caminhos ao longo dos quais um planeta que passa se move e conhecer o raio R do planeta observador, podemos desenhar um triângulo retângulo conectando o planeta que passa, o centro do planeta observador e o polo do planeta observador, com um pequeno ângulo? A trigonometria simples nos dará a distância D entre os planetas durante a passagem, onde

$$

$$D = R / tan \; \ alpha$$

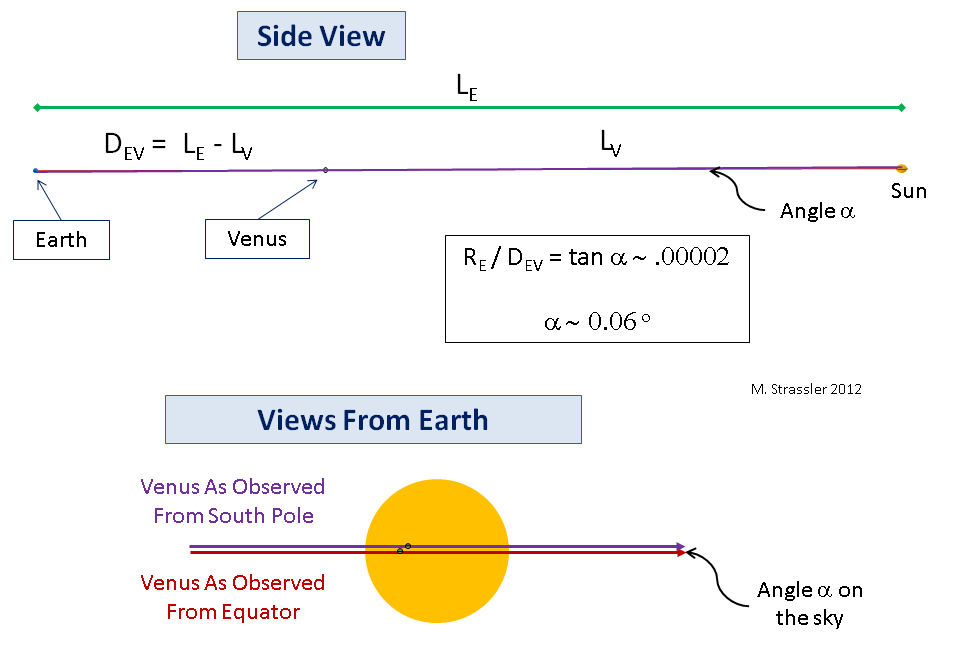Fig. 7

O mesmo vale para a Terra, Vênus e o Sol, exceto que a Terra e Vênus são tão pequenos em comparação com a distância entre eles e o Sol que o ângulo α será igual a cerca de 1/20 °! (Esta é uma quantidade bastante pequena, mas bastante mensurável, embora uma medida exata da distância ao Sol, que os astrônomos do século 18 desejassem obter, exigiria uma medição tecnicamente precisa bastante complicada da magnitude de um pequeno ângulo). Como não vou desenhar um ângulo tão pequeno, você deve aceitar minha palavra de que o que está acontecendo é uma versão do que descrevi na fig. 6, com planetas e uma estrela (o Sol) muito menor do que pintada lá, com relação às distâncias. Até a imagem na fig. 7 torna os planetas muito maiores do que são. Mas a idéia permanece inalterada: a distância D _EV entre a Terra e Vênus durante a passagem pode ser determinada medindo o ângulo de paralaxe α (parte inferior da Fig. 7; observe que o diâmetro angular do Sol é de cerca de 1/2 °).

No entanto, ainda existem muitas perguntas:

• Eu disse como medir D _EV , a distância da Terra a Vênus durante a passagem. Mas não era nosso objetivo medir _E e _V , a distância da Terra ao Sol e de Vênus ao Sol?
• Ninguém foi ao pólo sul da Terra para observar a passagem de Vênus em 1761 ou 1769.
• Eu assumi órbitas perfeitamente alinhadas da Terra, Vênus e a posição do Sol, de modo que, de um ponto no equador da Terra, era possível ver Vênus se movendo ao longo do equador do Sol. Mas, na verdade, não é esse o caso, e nem parece um passo a passo típico (e em 2012 também não).
• O ângulo α é pequeno o suficiente para ser medido com precisão - especialmente nos dias anteriores à fotografia e às mensagens instantâneas, na ausência de indicações claras da localização do polo norte do Sol, o que dificulta a comparação precisa das medidas do caminho de Vênus feitas a partir de dois pontos diferentes da Terra. No entanto, o objetivo principal era medir o ângulo não inferior a 1 parte em 500 (0,2%) (embora, devido ao efeito de gota preta, o resultado estivesse mais próximo de 1 parte em 50 (2%)).

Como lidar com esses problemas?

Primeiro, como você mede D _EV para medir os valores desejados, L _E e L _V ? É simples - já conhecemos todos os relacionamentos, em particular, já conhecemos L _E / L _V (aproximadamente, da Fig. 4, ou, se abordarmos a questão com mais cuidado, podemos calcular e com mais precisão) a partir do ângulo máximo γ _max entre Vênus e O sol do ponto de vista da terra. Também sabemos que D _EV = _E - _{E V} = _E (1 - _E / _E ) da Fig. 7. Portanto, podemos obter um valor aproximado de L _E usando:

$$

$$L_E = D_ {EV} / (1 - L_V / L_E) = R / tan \; α / (1 - sen \; \ gama_ {max})$$

onde α é o ângulo de paralaxe medido durante o trânsito e γ _max é o ângulo máximo entre Vênus e o Sol (Fig. 5). Medidas mais precisas requerem geometria mais complexa, mas com a mesma ideia básica.

Segundo, mesmo que as órbitas dos planetas estivessem perfeitamente alinhadas, duas dimensões do caminho de Vênus não precisam ser medidas a partir do equador e do polo da Terra. Eles podem ser medidos a partir de duas latitudes. A geometria se torna um pouco mais complicada, mas não muito, mas o princípio permanece (veja a Fig. 8).


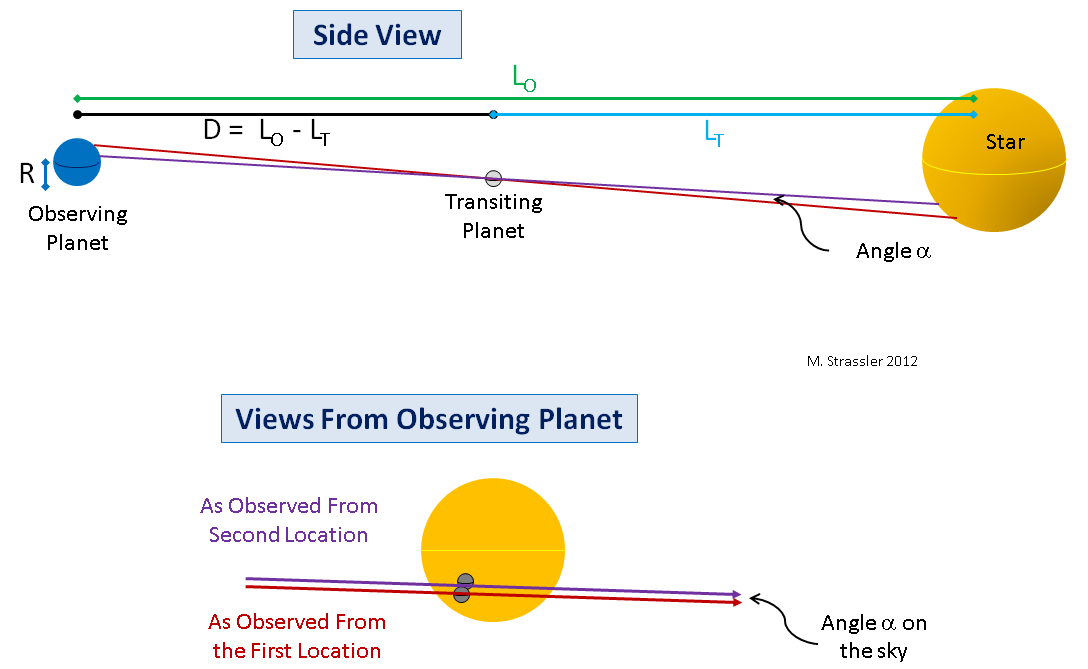Fig. 8

Terceiro, mesmo sem alinhamento perfeito, um pequeno ângulo de paralaxe aparecerá ao medir valores de dois pontos diferentes da Terra, e se esse ângulo for bem medido, essa medição poderá ser transformada (através de equações um pouco mais complexas) em D. Isso é mostrado na Fig. 8, para baixo.

A quarta questão é o problema historicamente complexo de medir a mudança angular do caminho de Vênus enquanto passa pelo ângulo α, nos leva a uma tentativa alternativa de medir o tempo - o tempo da viagem, ou simplesmente o início e o fim da passagem, e não os ângulos. A primeira opção foi proposta por Halley com base nas idéias de Gregory, e a segunda, como uma melhoria adicional, foi proposta por Joseph Nicola Delille . O método Halley não exigia sincronização de relógio em diferentes lugares da Terra; O método de Delil necessário, portanto, foi baseado em uma tecnologia de relógio mais avançada.

Mesmo no século XVII ou XVIII, é muito mais fácil medir com precisão o intervalo, ou os momentos do início e do fim de um eclipse, do que medir com precisão a localização de Vênus em relação ao disco do Sol, especialmente na ausência de uma fotografia. Na fig. A Figura 9 mostra que os caminhos violeta e vermelho de Vênus cruzando o Sol têm comprimentos ligeiramente diferentes porque não o cruzam em um único lugar, o que significa que a duração da passagem será diferente pelo tempo associado ao ângulo de paralaxe. Infelizmente, tudo se torna mais complicado do que parece à primeira vista - a Terra gira e se move ao redor do Sol, de modo que o observador percorre uma distância considerável durante a passagem de Vênus através do disco do Sol. Portanto, é necessário muito esforço (os cálculos são bastante complicados, embora com computadores modernos sejam muito mais simples) para determinar a diferença nos intervalos de tempo do início e do final da passagem observados por dois observadores diferentes na Terra, dependendo da distância do Sol.

Halley, no início do século XVIII, entendeu todos os princípios geométricos necessários (se você subtrair a fraseologia e o estilo desatualizados de inglês de seus textos, ficará surpreso com o fato de suas complexas declarações parecerem modernas e você verá que os cientistas há trezentos anos eram muito semelhantes aos cientistas de hoje, possuía a mesma inteligência e faltava apenas a tecnologia científica de hoje).


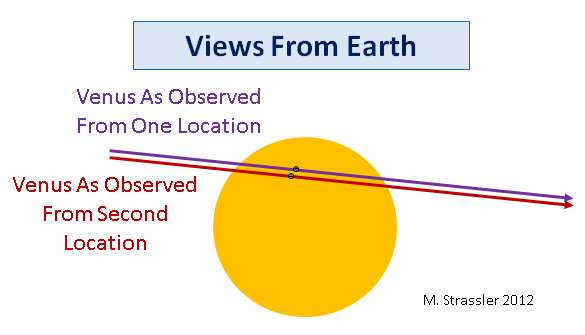Fig. 9

Tudo isso sugere que a paralaxe - a diferença na posição visível atribuída a Vênus em relação ao Sol do ponto de vista dos observadores que o medem ao mesmo tempo, mas de diferentes lugares da Terra - tem sido historicamente um método muito importante pelo qual determinou o tamanho do sistema solar. Hoje, métodos mais poderosos estão disponíveis para nós, mas você pode estar interessado no fato de que o que você vê hoje no céu é de grande importância histórica, ou pode simplesmente apreciar a vista de Vênus, majestosamente se movendo em torno de nossa estrela.