
Então você é um programador. Por que você precisa de polinômios? Por exemplo, então, que é uma boa argila geométrica, da qual você pode moldar coisas diferentes.
No
artigo que explica a essência da análise matemática usando python, sangue e dinamite como exemplo, pode-se ver que você pode analisar e sintetizar funções arbitrárias como polinômios. No entanto, não é necessário trabalhar especificamente com funções. Às vezes, pode ser necessário modelar um spline a partir de vários pontos ou propriedades, como tangentes de curvas. Por exemplo, você precisa fazer algum tipo de animação, ou um bom efeito de vídeo, ou desenhar uma curva passando por determinados pontos, ou criar uma superfície plana em um lugar e curvada em outro.
Polinômios, inclusive os splines, nem sempre são a melhor ferramenta para essa tarefa, mas possuem alguns recursos que os programadores realmente apreciam. Eles são simples e versáteis por natureza e, mais importante, muito eficazes em termos de desempenho. Tomemos, por exemplo, o seguinte polinômio:
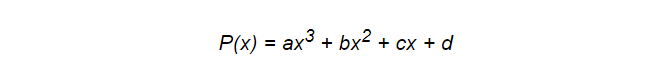
Para calcular, são necessárias apenas 6 ações de multiplicação e 3 adições. Isso é importante porque seu modelo estará constantemente sujeito a computação. Mas aqui podemos realizar otimização. O esquema de Horner nos ajudará com isso. Com sua ajuda, o mesmo polinômio pode ser escrito como

E isso são apenas 3 multiplicações e 3 adições. Veja bem, nós apenas começamos e você já aprendeu a se livrar de um terço dos cálculos.
Interpolação polinomial
A tarefa de adaptar um polinômio de grau
n a
n + 1 pontos no espaço é chamada interpolação polinomial. Existem várias maneiras de implementá-lo. Você pode usar as fórmulas de interpolação de
Newton ou
Lagrange , mas a maneira mais fácil de obter o polinômio de interpolação é resolver um sistema de equações lineares.
Se um polinômio passa por um ponto, então obviamente podemos dizer que
P (xi) = yi . Suponha que desejemos adaptar um polinômio a um conjunto de três pontos. Isso significa que:

No caso geral, não podemos traçar uma linha através de três pontos arbitrários. E então temos que dobrá-lo, formando uma parábola. Ou, em outras palavras, introduza um polinômio de segundo grau, também conhecido como função quadrática.

Como xs e ys são conhecidos, precisamos apenas resolver o sistema e descobrir os coeficientes a, b, c, e como esse sistema consiste em três equações e três variáveis, geralmente podemos obter uma única solução.
Para garantir isso, tente mover a posição dos três pontos no gráfico inferior e veja o que acontece.

Este gráfico também é muito útil para a análise mental de sistemas lineares. No caso geral, é impossível ajustar uma linha reta em três pontos, assim como é impossível encontrar uma solução para um sistema de n equações com n-1 variáveis desconhecidas. Mas às vezes é possível. Por exemplo, nos casos em que alguns dos pontos coincidem ou todos estão intencionalmente localizados em uma linha reta.
A situação inversa é ainda mais interessante. Podemos desenhar um número infinito de parábolas através de dois pontos dados. Todos eles são igualmente adequados como uma solução para o problema. E, ao mesmo tempo, não podemos obter uma solução excepcionalmente melhor para sistemas de n equações e n + 1 variáveis.
Mas e se ainda for possível? E se pudermos introduzir algum critério adicional para escolher a opção mais adequada?
Síntese
Questões semelhantes nos levam ao território da síntese polinomial. No nosso caso, este é um cruzamento entre séries polinomiais e interpolação polinomial. Usando séries, podemos modelar uma função com base em suas derivadas em algum momento, e usando síntese, podemos usar pontos e derivadas (e não apenas eles, mas mais sobre isso em outro momento).
A derivada de uma função está intimamente relacionada às propriedades geométricas de seu gráfico. A primeira derivada determina a tangente da inclinação da tangente e a segunda determina a curvatura.
Suponha que precisamos definir uma função passando por dois pontos, conhecendo sua tangente nos dois pontos. Nesse caso, podemos sintetizá-lo facilmente como um polinômio.
Como antes, precisamos escrever um sistema de equações. Agora precisamos de quatro condições, portanto devemos escolher um polinômio de grau 3, ou seja, uma função cúbica.
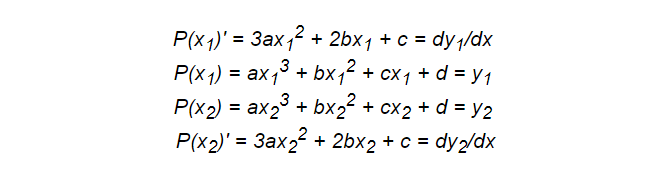
Algumas das equações são baseadas em pontos, enquanto outras são derivadas. Os integrais também podem ser adicionados aqui para introduzir as propriedades inteiras necessárias, o que torna essa técnica bastante eficaz.
Mas continuaremos a considerar uma função conectando dois pontos de uma linha suave contínua com restrições tangenciais nesses pontos.


Fenômeno de Runge
A interpolação polinomial tem uma propriedade desagradável, que se manifesta em um aumento no crescimento de oscilações em ambas as extremidades do intervalo, com um aumento no número de pontos. Esse fenômeno é chamado de fenômeno Runge. Limita a possibilidade de usar interpolações polinomiais simples.
Outra desvantagem dessa abordagem é sua natureza global, ou seja, uma mudança em toda a função, juntamente com a menor mudança na posição de pelo menos um ponto. Em combinação com oscilações, o próprio resultado é o caos.

Nós Chebyshev
Uma das maneiras de combater o caos é selecionar uma malha especial para interpolação -
nós Chebyshev . Estes são valores especiais de x que são obtidos dividindo um semicírculo com um raio de 1 em fragmentos iguais e projetando-os no eixo x.
Em geral, uma certa magia matemática está oculta nessa técnica, mas, de um ponto de vista pragmático, pretende-se minimizar o fenômeno Runge. E, embora não permita tornar a interpolação completamente previsível, tudo funciona de forma estável no intervalo (-1: 1).

Obviamente, você pode estender o intervalo ao longo do eixo X o quanto for necessário, usando a transformação afim unidimensional. Não é necessário aderir ao segmento
(-1; 1) .
Mas a interpolação, ao mesmo tempo, mantém sua onipresença. Alterar o primeiro ponto ainda afeta a operação da função próxima ao último, embora não seja tão significativa.
Splines
Existem várias variedades de splines, mas todas elas são unidas por um cenário de aplicativo. Assim que, por algum motivo, a interpolação global deixar de ser adequada para nossas tarefas, podemos dividir nosso intervalo em fragmentos menores e definir funções individuais para interpolação em cada um deles.
A única coisa que precisamos considerar é a necessidade de conectá-los no final para manter a continuidade. Se garantirmos a continuidade não apenas da função final definida por partes, mas também de sua primeira derivada, nesse caso as tangentes de cada um de seus segmentos coincidirão e seu cronograma parecerá suave.
Existe uma certa
classificação de splines. Por exemplo, use um spline polinomial composto por dois fragmentos. Se cada fragmento é determinado por um polinômio de terceiro grau, é chamado de cúbico. Pode possuir, por exemplo, uma propriedade como a continuidade da primeira derivada, uma vez que coincidem as tangentes na junção dos fragmentos. Seus fragmentos não têm largura igual. Não é de origem natural, pois podemos controlar os derivativos em seus fins. E, claro, esse é um spline de interpolação, porque passa exatamente pelos pontos da grade que indicamos.

Conclusão
A probabilidade de você ter que colocar em prática sua própria interpolação é extremamente pequena. Existem muitas soluções prontas e, na maioria dos casos, você só precisa escolher a ferramenta certa para o trabalho. Essa área do conhecimento não é tão complicada, mas o número de palavras e nomes desconhecidos pode ser descartado.
O objetivo deste guia era fornecer a você um entendimento básico das idéias usadas para trabalhar com polinômios e splines. Em nenhum caso ele finge estar completo, porque, de fato, livros inteiros são escritos em cada um dos pequenos capítulos deste material. Mas esperamos, pelo menos, que a abordagem interativa da apresentação neste material seja útil não apenas para uma breve introdução, mas, se surgir essa necessidade, ajudará você a dominar tópicos mais avançados.
