Cosmologia - Stanford. Resumo. Palestra 1

Este artigo abre uma série de notas de aula sobre cosmologia da Stanford University. As palestras em inglês estão disponíveis em: Cosmology (2013) - Leonard Susskind - Stanford University . Eu assisti a palestra em vídeo e delineei com prazer. O professor Leonard Susskind explica muito acessível e divertido. É evidente que ele é uma pessoa talentosa e um excelente professor.

A Universidade de Stanford também é famosa pelo fato de que nosso destacado compatriota Andrei Linde trabalha lá, que provavelmente receberá em breve o Prêmio Nobel de física por sua contribuição à cosmologia moderna. Quem se importa, eu aconselho você a assistir sua palestra pública As muitas faces do universo .

Esta sinopse é minha tentativa de auto-educação. Eu ainda escreveria para mim mesmo em um caderno. Mas eu decidi combinar negócios com prazer. Espero que seja interessante para alguém também.

Faça imediatamente uma reserva que tentei fazer anotações próximas ao texto original. No entanto, em alguns lugares, permiti-me complementar ou generalizar as declarações do professor com base em minha própria experiência como físico especialista. Isso foi feito apenas para facilitar a compreensão, compreensão e assimilação do material.

Neste artigo, é oferecida uma sinopse da palestra 1. Talvez uma sequência seja exibida mais tarde.

Revisão histórica

A cosmologia é um assunto muito antigo. A história da cosmologia remonta milhares de anos. Em particular, os gregos antigos conheciam a cosmologia há muito tempo.

Essas palestras abrangem o período de tempo não superior à segunda metade do século XX, quando Edwin Hubble descobriu a lei da expansão do universo.

Se falamos de cosmologia como ciência, esse é um campo de conhecimento relativamente novo. A cosmologia moderna remonta à descoberta da radiação das relíquias de microondas e à formulação da teoria do big bang . E isso só aconteceu na década de 1960.

Até este ponto, a cosmologia não era um ramo da física, mas pertencia às ciências naturais. Ou seja, na cosmologia prevaleceu a abordagem fenomenológica: observação, medição, classificação, catalogação, etc.

Naquela época, a precisão das medições era baixa. E, portanto, era impossível formular afirmações exatas. Havia equações, mas eram incorretas e imprecisas. Os físicos sempre estiveram envolvidos no processo de estudo, uma vez que estrelas, galáxias e outros corpos celestes possuem características físicas, como momento angular, por exemplo. Químicos físicos também estavam envolvidos, uma vez que os corpos celestes têm uma composição química.

No entanto, a atitude em relação ao próprio Universo como um objeto físico, o Universo como um sistema que deve ser estudado matematicamente usando um conjunto de princípios físicos e as equações corretas exatas correspondentes - essa é uma abordagem relativamente jovem.

Propriedades do Universo

Nessas palestras, o Universo é considerado como um sistema físico. E vamos estudá-lo usando equações. Podemos começar nossa exploração do universo com algumas observações gerais.

Isotropia

Portanto, a primeira observação, que, em geral, pode não ser absolutamente precisa, assim como toda a física não é absolutamente precisa, é que o Universo é isotrópico .

Isotropia significa que o universo parece o mesmo em qualquer direção. Obviamente, isso é verdade apenas para distâncias suficientemente grandes. Se você olhar muito de perto, a isotropia pode não ser observada devido a não homogeneidades locais, por exemplo, devido ao formato de nossa galáxia.

Uniformidade

Se o Universo é isotrópico, pode-se argumentar com grande certeza que o Universo também deve ser homogêneo . Homogeneidade não significa uniformidade em todas as direções, mas em todo lugar. Ou seja, em larga escala, o Universo parece o mesmo, independentemente de onde o observador esteja localizado - em nossa galáxia ou em alguma outra, que está muito, muito longe de nós.

Galáxias

Galáxias na escala do Universo são efetivamente pontos de concentração de massa . Podemos tratá-los como pontos materiais. O número aproximado de galáxias na parte visível do universo é de cem bilhões $$$10 ^ {11} = 100 \, 000 \, 000 \, $ 00$ . Por sua vez, cada galáxia também contém aproximadamente $$$10 ^ {11}$ cem bilhões de estrelas. Devemos lembrar que este é o número de galáxias apenas dentro da esfera que podemos ver. Somente até onde os astrônomos podem ver com telescópios. Ou seja, o mais longe que podemos ver está a uma distância de onde a luz conseguiu nos alcançar por toda a existência do Universo: cerca de 13 bilhões de anos.

Um fato interessante. O número total de estrelas na parte visível do universo $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ , e se cada estrela tem uma média de 10 planetas, acontece que $$$10 ^ {23}$ - o número de planetas Avogadro no universo. Toupeira planetária de substância! (o professor ri)

Um argumento contra a homogeneidade do universo. Refutação

Considere um pedaço do universo onde estamos. Temos certeza, porque vemos que o Universo é isotrópico . Assumimos que o universo também é homogêneo . Mas o que aconteceria se o universo não fosse homogêneo?

Se o Universo é isotrópico, a única maneira de não ser homogêneo é ter uma estrutura na forma de uma espécie de concha.


A hipótese de um universo heterogêneo. À esquerda, um universo isotrópico homogêneo; à direita, um universo isotrópico não homogêneo. A cruz no centro nos indica.

Se assim fosse, em qualquer outro ponto o Universo não pareceria isotrópico. Ou seja, se não queremos acreditar que, de alguma forma, estávamos exatamente no centro do universo, e para que todo o universo tenha simetria esférica ao nosso redor, teremos de admitir que o universo não é apenas isotrópico, mas também homogêneo.

Princípio cosmológico

Portanto, se não acreditamos que estamos localizados exatamente no centro do universo, o universo deve ser homogêneo. Um universo homogêneo significa que o universo é uniformemente preenchido com partículas (galáxias) em todo o volume. Isso é chamado de princípio cosmológico . O princípio cosmológico é verdadeiro, porque nossas observações indicam isso, é claro, com algum grau de aproximação.

Alguns astrônomos afirmam que observaram heterogeneidades em larga escala no universo. O palestrante duvida da confiabilidade dessas fontes e declarações.

Obviamente, a idéia da homogeneidade do universo não é absolutamente exata. Mesmo o fato de existirem galáxias já sugere que existem heterogeneidades. A propósito, não existem apenas galáxias, mas também aglomerados de galáxias. No entanto, em uma escala bastante grande, aproximadamente da ordem de 1 bilhão de anos-luz, o Universo parece homogêneo.

A princípio, o princípio cosmológico era apenas um postulado. Porém, com o acúmulo de dados observacionais, foi confirmado de maneira cada vez mais confiável e, no final, foi descoberta a radiação de microondas por relíquia, o que indica que a distribuição inicial da matéria no Universo era altamente homogênea.

Declaração do problema físico

Existe um gás uniforme de partículas galácticas. E cada galáxia interage com outras galáxias. As galáxias como um todo são eletricamente neutras. Mas eles não são neutros gravitacionalmente. Eles interagem através da gravidade newtoniana. E esta é a única força importante em larga escala. A gravidade atua nas galáxias e tenta reuni-las.

Então, se você olhar para qualquer ponto do Universo e se perguntar para onde ele deve se mover, pode adivinhar que, de todos os lados, está cercado pela mesma quantidade de massa. Seguindo essa lógica, pode-se supor que nenhuma galáxia deve se mover e o Universo deve ser estático, pois o resultado de forças que agem em qualquer ponto do Universo é zero. Isso está absolutamente errado!

E agora temos equações newtonianas de movimento para o universo. Você pode ouvir que o Universo em expansão está de acordo com a teoria geral da relatividade de Einstein, e que antes da teoria geral da relatividade, a lei do Universo em expansão era incompreensível. Isso simplesmente não é verdade. Talvez isso tenha sido tão historicamente. Mas este é apenas um fato histórico sobre datas, não sobre lógica. Newton poderia obter as equações de um universo em expansão. E agora faremos isso como Newton deveria ter feito.

Sistema de coordenadas

Em qualquer problema físico, a primeira coisa a fazer é introduzir um sistema de coordenadas. Em vez de escolher o passo da grade à distância: 1 metro, um milhão de quilômetros, mil anos-luz, escolheremos uma grade para que seus nós sejam rigidamente fixados às galáxias. Como o universo é homogêneo, podemos fazê-lo. Então as galáxias sempre permanecerão aproximadamente nas mesmas coordenadas, independentemente do que acontecer ao universo. Ou seja, as galáxias parecem estar "congeladas" na grade de coordenadas.

Não é de todo óbvio que isso possa ser feito. Se as galáxias se movessem completamente por acidente e em direções completamente diferentes, não poderíamos fazer isso. Mas vemos que as galáxias se movem por acaso. Vemos que as galáxias se movem em conjunto, exatamente como se estivessem embutidas em uma determinada grade de coordenadas. E o que vemos nos permite fazer isso, porque as velocidades das galáxias em relação umas às outras são consistentes e não acidentais.

Nós introduzimos uma grade $$$(x, y, z)$ . Essas coordenadas não são medidas em unidades de comprimento. Se considerarmos duas galáxias separadas por um intervalo $$$\ Delta x$ então a distância $$$D$ entre eles (em metros) é expresso como

$$

$$D = a \, \ Delta x$$

onde $$$a$ É um parâmetro de escala, que pode ser uma constante, mas de um modo geral, pode não ser. O parâmetro de escala pode depender do tempo. $$$a = a (t)$ .

Assim, pelo teorema de Pitágoras, a distância entre duas galáxias é geralmente escrita como

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

E claro, o parâmetro $$$a$ não é uma constante. Se fosse uma constante, as galáxias seriam estáticas, não se moveriam em lugar algum. E não é isso que estamos observando. Vemos que eles voam separados.

Direito de Hubble

Escrevemos a velocidade relativa entre duas galáxias. Diferenciamos a fórmula anterior no tempo. Levamos em conta que $$$\ Delta x$ - Este é um intervalo fixo, que não pode ser alterado de acordo com as condições para a construção de um sistema de coordenadas. Então

$$

$$\ mathcal {V} = \ ponto {a} \, \ Delta x$$

onde usamos a notação $$$\ ponto {a} = da / dt$ .

Agora escrevemos a razão da velocidade relativa de duas galáxias para a distância entre elas

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ ponto {a} (t)} {a (t)}$$

Note que $$$\ Delta x$ é reduzido e essa proporção não depende de coordenadas. Ou seja, essa fórmula é válida para duas galáxias, não importando a que distância ou distância elas estejam.

Essa relação é chamada de parâmetro constante do Hubble.

$$

$$H (t) = \ frac {\ ponto {a} (t)} {a (t)}$$

e não depende das coordenadas. Então você pode escrever o mesmo no formulário padrão

$$

$$\ mathcal {V} = H \, D$$

A velocidade relativa de duas galáxias é proporcional à distância entre elas.

Você precisa entender que nunca teríamos escrito se o Hubble não tivesse descoberto sua lei. A lei de Hubble, por outro lado, não é tão surpreendente. Há um ditado: "Não é de surpreender que o cavalo mais rápido cavalgue à frente de todos". Quanto mais rápido você se move, mais você fica. E este é um fato que o Hubble descobriu.

Massa de matéria no universo

Considere algum volume $$$\ Delta x \, \ Delta y \, \ Delta z$ . Nós fazemos uma pergunta: qual massa está concentrada neste volume? Vamos $$$\ nu$ É a massa de uma substância em um volume elementar $$$dx \, dy \, dz$ (em quilogramas). Então a massa em volume $$$\ Delta x \, \ Delta y \, \ Delta z$ é igual a

$$

$$M = \ nu \, \ Delta x \, \ Delta y \, \ Delta z$$

Qual é o volume métrico dessa área? Desde $$$D = a \, \ Delta x$ nós podemos escrever

$$

$$V = a ^ 3 \, \ Delta x \, \ Delta y \, \ Delta z$$

Qual é a densidade da substância nesta área? Por definição, a densidade é $$$\ rho = M / V$ , ou seja, levando em consideração as duas fórmulas anteriores, obtemos

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

Essa é a densidade física padrão de uma substância.

Embora a quantidade total de massa em volume $$$\ Delta x \, \ Delta y \, \ Delta z$ não muda, como as galáxias são “congeladas” na grade de coordenadas, a densidade absoluta da matéria no mesmo volume pode mudar, uma vez que o parâmetro $$$a (t)$ depende do tempo.

Teorema de Newton

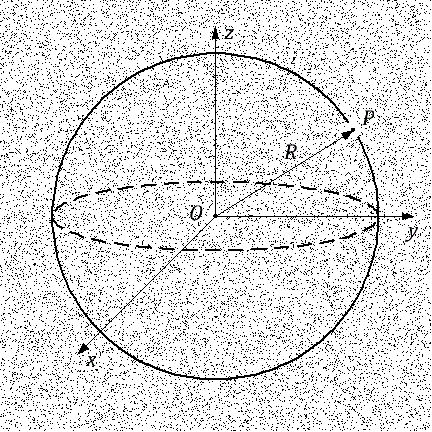Ilustração para o teorema de Newton

Considere dois galactiti. Sempre podemos colocar um deles na origem. Deixe a galáxia $$$O$ está na origem e a galáxia $$$P$ está a alguma distância dela.

O teorema de Newton afirma que a força da gravidade agindo em uma galáxia $$$P$ depende apenas da quantidade de massa dentro da esfera centralizada na origem $$$O$ e passando pela galáxia $$$P$ . A segunda afirmação do teorema de Newton é que toda a massa dentro desta esfera pode ser considerada concentrada no centro na origem no ponto $$$O$ , desde que a massa dentro da esfera seja distribuída, se não uniformemente, pelo menos isotropicamente .

Em outras palavras, o efeito de toda a massa dentro da esfera na galáxia $$$P$ equivalente a se essa massa estivesse concentrada em um único ponto $$$O$ , que é o centro da esfera.

Equações newtonianas de movimento

Encontre a distância entre galáxias $$$P$ e $$$O$ . Galáxia $$$P$ tem coordenadas $$$(x, y, z)$ ou seja, a distância do centro à galáxia $$$P$ é igual a

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

Podemos introduzir a notação

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ não medido em metros, mas nas mesmas unidades que $$$x$ , $$$y$ e $$$z$ e não depende do tempo. Então

$$

$$D = a (t) \, R$$

Agora registramos a velocidade e aceleração da galáxia $$$P$

$$

$$\ mathcal {V} = \ ponto {a} (t) \, R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \, R$$

Agora temos que equiparar aceleração $$$\ mathcal {A}$ à aceleração associada a toda a massa gravitacional dentro de uma esfera de raio $$$R$ . Denotar a massa da galáxia $$$P$ para $$$m$ e a massa de toda a matéria dentro da esfera além $$$M$ . Então a força da gravidade agindo na galáxia $$$P$ é igual a

$$

$$F = -G \ frac {m \, M} {D ^ 2}$$

onde $$$G = 6.67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - constante gravitacional. O sinal de menos na fórmula significa que é uma força atraente.

Agora você pode gravar a aceleração da galáxia $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

Igualamos duas expressões para $$$\ mathcal {A}$ e consiga

$$

$$\ ddot {a} (t) \, R = -G \ frac {M} {D ^ 2}$$

Levamos em conta que $$$D = a \, R$ então

$$

$$\ ddot {a} \, R = - \ frac {M \, G} {a ^ 2 \, R ^ 2}$$

Divida os dois lados por $$$a \, R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \, G} {a ^ 3 \, R ^ 3}$$

Encontre o volume da esfera

$$

$$V = \ frac {4} {3} \ pi \, D ^ 3 = \ frac {4} {3} \ pi \, a ^ 3 \, R ^ 3$$

Multiplicamos o numerador e o denominador do lado direito por $$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \, G \, \ rho$$

Esta equação é independente de $$$R$ , e é verdade para qualquer galáxia no universo. Esta equação é a equação fundamental central da cosmologia .

Uma das conseqüências dessa equação é que é impossível que o Universo seja estático se não estiver vazio. A partir desta equação, segue-se que o Universo pode ser estático apenas se estiver vazio.

Podemos reescrever essa equação, dado que $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \, \ nu} {a ^ 3}$$

Essa equação foi obtida pela primeira vez no contexto da teoria geral da relatividade por Alexander Friedman. Essa equação não nos diz se o universo está se expandindo ou se contraindo. Diz apenas que a segunda derivada do fator de escala é negativa. Ou seja, se o Universo se expande, diminui a velocidade e, se o Universo encolher, acelera.

De fato, o universo está se expandindo e não diminuindo a velocidade. Acabamos de fazer o que Newton poderia fazer e que todos os cosmólogos consideraram certo até 1998. Esse modelo era geralmente aceito e era chamado de modelo padrão do Universo até que a expansão acelerada do Universo fosse descoberta abertamente. Até agora, o lado direito da equação tem apenas um termo. De fato, deve haver vários termos relacionados à teoria geral da relatividade.

Velocidade de Partida

Agora escreva toda a energia da galáxia $$$P$ como a soma da cinética e potencial

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D}$$

A energia pode ser positiva ou negativa, dependendo da razão entre esses dois termos. Também é importante lembrar que a energia total da partícula $$$P$ salvo. Se a energia total for positiva, a partícula não poderá voltar. Uma partícula retorna apenas quando a energia total é negativa. O caso limite é que a energia total é zero. Resolva a equação $$$E = 0$ para $$$\ mathcal {V}$ para encontrar a velocidade de partida.

$$

$$\ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

Assim como uma galáxia $$$P$ todo o universo pode ter uma velocidade maior que a velocidade de partida, menor que a velocidade de partida ou igual à velocidade de partida. Se a velocidade do Universo for maior que a velocidade da partida, ela se expande e nunca começa a encolher; se o Universo tem uma velocidade abaixo da velocidade da partida, mais cedo ou mais tarde começará a encolher.

Reescreva a equação da energia total

$$

$$\ frac {1} {2} m \, \ ponto {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = E$$

Equação de Friedman

Considere o caso em que a velocidade do universo coincide com a velocidade da partida.

$$

$$\ frac {1} {2} m \, \ ponto {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = 0$$

Simplifique a expressão: divida por $$$m$ , multiplique por 2, divida por $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ ponto {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

No segundo termo, multiplicamos o numerador e o denominador por $$ . Então, no denominador, obtemos o volume métrico da esfera $$$V$ . Dado que $$M / V = ρ , obtemos$M/V = \rho$

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{8\pi}{3}G\rho$$

Isso é chamado de equação de Friedman . É equivalente à equação newtoniana obtida acima. Como assumimos que a energia total é zero, esse universo se expande, assintoticamente diminuindo para zero, mas nunca cruza o zero e não começa a encolher.

Lembre-se agora que$$$\rho = \nu /a^3$ . Reescreva a equação de Friedman

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{8\pi}{3}\frac{\nu G}{a^3}$$

Parâmetro $$ν é muito flexível. Depende completamente da nossa escolha da grade. E de um modo geral, podemos até escolher para que$\nu$$$$\frac{8\pi}{3}\nu G = 1$ . Então

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

O lado direito desta equação é sempre positivo e, portanto, a taxa de expansão
$$Never a nunca se torna igual a zero. Lembre-se agora que$\dot{a}$$$˙ a /a=Héo parâmetroconstantedo Hubble. Também resulta da equação que o parâmetro Hubble nunca muda de sinal. No entanto, ainda está desacelerando. O parâmetro Hubble se torna cada vez menos com o tempo. Essa equação é extremamente importante para toda cosmologia. Uma maneira simples de resolvê-lo é procurar uma solução de um determinado tipo, ou seja, procuraremos uma solução na forma$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

onde $$$c$ e $$p são algumas constantes.$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

Obtivemos uma solução para a equação de Friedman.


Gráfico da solução da equação de Friedman

O Universo real segue essa decisão apenas até um certo ponto no tempo e começa a acelerar. Newton poderia fazer isso. Ele chegou muito perto. Fez todas as perguntas certas. O palestrante está confiante de que Newton provavelmente fez isso e recebeu essa decisão. No entanto, essas informações sobre o universo eram contrárias às suas visões religiosas e, portanto, ele não publicou suas descobertas.