Posso ganhar jogos de azar? Simulação Python

Oi Geektimes.

No processo de ociosidade, surgiu a idéia de estudar vários jogos de azar, ao mesmo tempo, para entender melhor como ele funciona. Os resultados, embora geralmente óbvios, foram interessantes o suficiente para serem compartilhados com o público.



Para quem os detalhes são interessantes, pergunto em cat.

Dados: Jogo de Dados

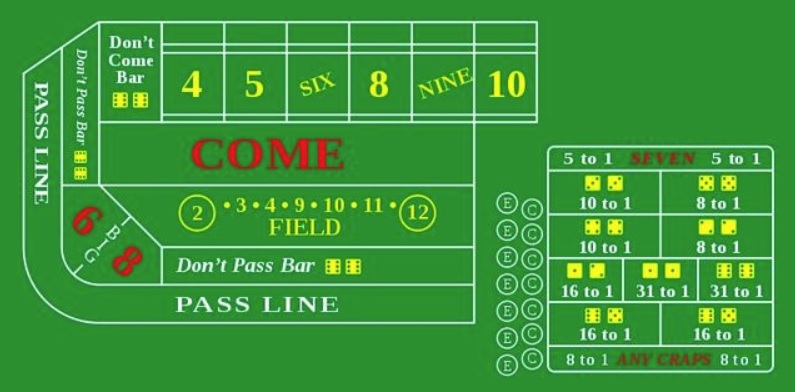
Provavelmente, uma opção intuitivamente simples e compreensível - existe um cubo com notas de 1 a 6, e a probabilidade de um determinado número cair é de 1/6. Mas jogar dessa maneira seria chato, então jogos com regras mais complexas são populares. Um jogo de azar popular é o craps , a imagem acima mostra uma imagem da mesa de jogo. Como você pode ver, há muito de tudo, mas não entraremos em sutilezas profundas.

Cada turno do jogo consiste em jogar dois dados, os pontos acumulados são somados. Como o artigo diz : “As regras do jogo são diretas: o jogador lança dois dados e, se a soma de pontos neles é 7 ou 11, ele vence, se 2, 3 ou 12 perderem. Quando uma quantidade diferente cai nos dados, o atirador os joga para uma combinação vencedora ou perdida. ”

Vamos ver o quanto você pode ganhar dessa maneira. Não é necessário ir a um cassino para isso; usaremos o Python para simular o jogo. Escrevemos uma função para um arremesso:

import random def shoot(): return random.randint(1,6) + random.randint(1,6) 

Escreveremos a função de simulação de um movimento de acordo com as regras acima.

 def move(): while True: val = shoot() print "Dice roll:", val if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False 

Vamos definir para o nosso jogador virtual uma quantia inicial de $ 100 e iniciar o processo do jogo. Deixe o nosso jogador fazer 100 apostas, cada vez 1u.e.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Começamos a simulação de 100 jogos e ficamos surpresos com o resultado, o jogador venceu e com uma margem notável de vitórias de derrotas: Vitória 63, Perda 37, Dinheiro 126. Aumentamos o número de jogos para 1000 e corremos novamente, o jogador venceu novamente: Vitória 680, Perda 320, Dinheiro 460 .

É claro que algo está errado aqui - um jogo em que o jogador sempre estaria no preto, dificilmente seria popular no cassino, simplesmente faliria. Vamos tentar descobrir.

Parece intuitivamente que, ao jogar um dado, a probabilidade de qualquer faceta cair é igualmente provável. E isso é verdade, mas no caso de um cubo. Se houver dois cubos, tudo ficará mais complicado. Por exemplo, o número 7 pode cair como 3 + 4, 2 + 5, 1 + 6, mas o número 12 pode cair apenas como uma combinação de 6 + 6.

No caderno Jupyter, construímos um cronograma para a perda de valores de 1 a 12 para 100 jogadas:

 from matplotlib import pyplot as plt %matplotlib inline y = [ shoot() for v in range(100) ] plt.hist(y) 

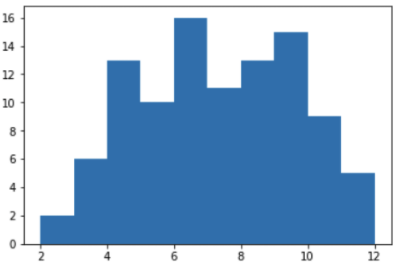
A suposição foi confirmada, e a quantidade do centro realmente cai com mais frequência. Assim, os números 7 e 11 realmente caem com mais frequência que 2,3 ou 12. E a probabilidade de obter uma combinação vencedora “7 ou 11” é realmente maior.

Como isso pode ser? Infelizmente, a resposta é simples - o autor do artigo citado acima simplesmente não entendeu completamente as regras do jogo. O texto “as regras do jogo são diretas: o jogador joga dois dados e, se a soma de pontos for 7 ou 11, ele vence, se 2, 3 ou 12 - ele perde ” está muito longe da verdade, e as regras dos dados não são tão diretas quanto parecem .

As regras reais para apostar na linha de passe se mostraram um pouco mais complicadas (existem outros tipos de apostas que as pessoas que desejam podem descobrir por si mesmas).

Mover 1 : Um rolo é feito. Se 7 ou 11 cair, o jogador ganha; se 2, 3 ou 12, o jogador perde. Se outro número cair, ele será lembrado sob o ponto de nome.

Mover 2 : Um rolo é feito. Se 7 cair, o jogador perde. Se o ponto cair, o jogador venceu. Se outros números caírem, a jogada é repetida (neste momento, os jogadores também podem apostar em outros números).

De fato, tudo é um pouco mais complicado do que o descrito na versão original. Adicionamos uma função de simulação levando em consideração regras mais precisas.

 def move(): point = 0 while True: val = shoot() if point == 0: # First move if val == 7 or val == 11: return True if val == 2 or val == 3 or val == 12: return False point = val else: # 2..N move if val == 7: return False if val == point: return True 

O resultado agora é mais parecido com a verdade: em 100 jogos, o jogador venceu 43 vezes, perdeu 57 vezes, o saldo no final do jogo foi de 86.u. dos 100 originais. Também é interessante que o número de vitórias tenha sido bastante grande e seja apenas um pouco menos de 50%. Essa é uma estratégia competente do ponto de vista do cassino - permite que você mantenha o interesse do participante no jogo (seria desinteressante perder o tempo todo), mas, ao mesmo tempo, o saldo de lucro do cassino permanece positivo e o saldo de dinheiro do jogador é negativo.

Vamos ver em mais detalhes o que é obtido para a simulação de 100 jogos.
- A chance de vencer no primeiro passo caiu em cerca de 20 casos.
- A chance de perder imediatamente no primeiro passo caiu em 15 casos.
- Nos 65 casos restantes, o jogo continua e tudo é complicado: a escolha vem de dois números, 7 e ponto, mas como você pode ver no gráfico acima, a probabilidade de um número "perdedor" cair 7 é máxima, o que em geral era para ser provado.

É interessante notar que a chance de ganhar em 45% é bastante alta. Então é possível ganhar? No curto prazo, por exemplo, em outra simulação, o jogador teve "sorte" e, em 100 jogos, aumentou seu capital virtual de 100 para 112 anos.



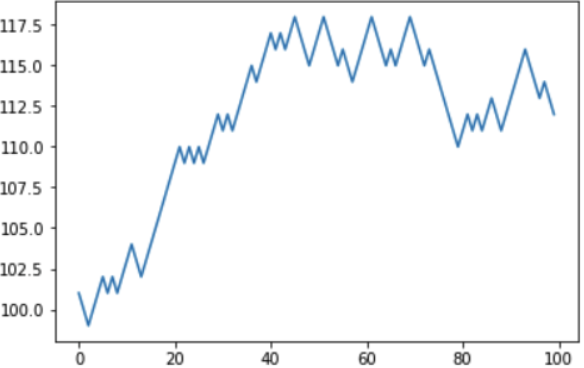
Mas a simulação seguinte já mostrava um saldo negativo: o jogador reduziu seu estado de 100 para 88 anos, perdendo, a propósito, os mesmos 12 anos "vencidos" na época anterior.

Se você aumentar o número de iterações para 1000, poderá ver como o saldo monetário do jogador pode parecer a longo prazo:



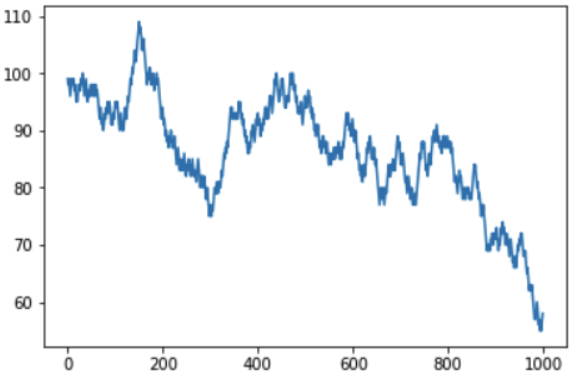
É claro que, com uma chance de ganhar cada jogo abaixo de 50%, a quantidade de dinheiro resultante na conta do jogador diminuirá gradualmente e a quantidade de lucro do cassino aumentará gradualmente. A propósito, no gráfico, as rajadas e quedas são visíveis e uma pergunta razoável pode surgir - elas podem ser previstas? Infelizmente, não, porque Rolamentos de dados são eventos independentes um do outro e os resultados anteriores não afetam de maneira alguma o seguinte. Você pode repetir a idéia principal mais uma vez - você pode ganhar uma ou até várias vezes, mas a longo prazo é impossível permanecer na vantagem no cassino, as regras do jogo são elaboradas para que o saldo não seja a favor do jogador.

Existem outros tipos de apostas no jogo de craps, e quem quiser pode analisá-las por conta própria.

Roleta americana

O próximo tipo popular de jogo é a roleta, considere sua versão americana.



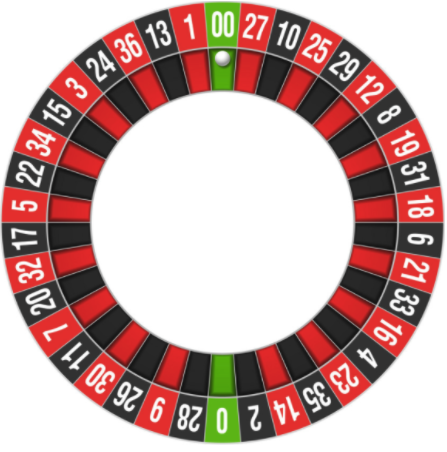
O campo de jogo da roleta é dividido em 38 células: 36 zonas com números + 2 zonas "zero" e "duplo zero". Uma bola jogada em uma roleta obviamente parará em uma das zonas. O jogador pode fazer uma variedade de apostas, das quais existem mais de 10 tipos, considere algumas delas.

Preto-vermelho (ou ímpar-par)

Um jogador vence se a aposta que ele mencionar coincidir. Obviamente, a probabilidade de preto ou vermelho seria 50/50, se não fosse por dois campos de zero - se eles acertarem, a aposta perde. Como no caso dos dados, isso aumenta a probabilidade de ganhar apenas um pouco menos de 50% - mas esse "pouco" é suficiente para ficar no vermelho.

Escreveremos a função de simular o movimento usando números aleatórios de 1 a 38, os últimos 2 dígitos serão considerados "zero".

 def move_roulette1(): val = random.randint(1,38) if val == 37 or val == 38: return False return val % 2 != 0 

Execute a simulação para 100 jogos, o código é o mesmo da simulação de dados, apenas mudamos a chamada de função.

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette1() if step is True: money_total += bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

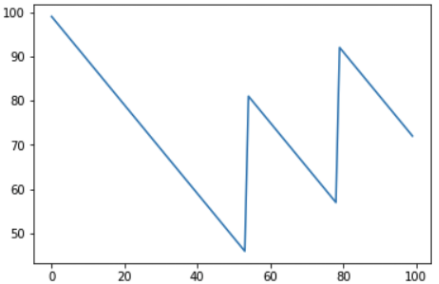
Resultado: em 100 tentativas, o jogador venceu 46 vezes e perdeu 54 vezes. O gráfico mostra que o jogador teve "altos" e "quedas", mas o saldo final ainda é negativo.



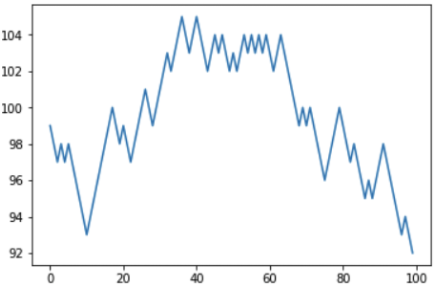
Quanto mais jogamos, mais fundo entramos em menos, e o cassino, respectivamente, em mais:



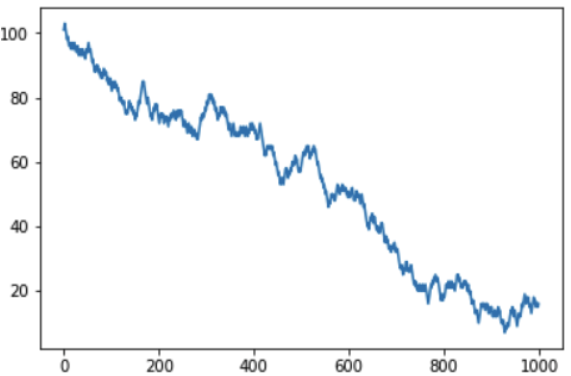
Houve uma pergunta do leitor por que eu não considerava a roleta européia com um campo "zero" - como você pode imaginar, a chance de ganhar lá é realmente maior, mas o princípio geral não muda. De fato, a diferença está apenas na "velocidade perdida". Aqui está o cronograma conjunto das versões americana e européia do jogo:


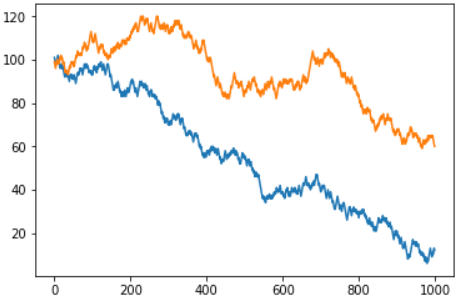
Quem quiser testar a versão européia da roleta com 37 slots, pode usar a segunda opção da função:

 def move_roulette1(): val = random.randint(1,37) if val == 37: return False return val % 2 != 0 

Aposte em um número específico

O jogador também pode apostar em um determinado número, a aposta na vitória é de 35: 1. Parece ótimo, mas é fácil adivinhar que a probabilidade de um determinado número de roleta cair é 1:38, ou seja, novamente, um pouco menos.

Vamos adicionar a função de aposta a um número específico:

 def move_roulette2(num): val = random.randint(1,38) return val == num 

Simulação, assumimos que o jogador coloca o número 10:

 money_total = 100 win = 0 loss = 0 for p in range(100): bet = 1 step = move_roulette2(10) if step is True: money_total += 35*bet win += 1 else: money_total -= bet loss += 1 print "Win", win, "Loss", loss, "Money", money_total 

Como resultado, o jogador venceu 2 vezes e perdeu 98 vezes, o saldo final é de -28.u.



Aposte em dois números

Você pode apostar em dois números - a chance de ganhar é maior, mas a aposta é menor e é de 17: 1.

Vamos escrever uma função:

 def move_roulette3(num1, num2): val = random.randint(1,38) return val == num1 or val == num2 

Para 100 tentativas da nossa simulação, o jogador venceu 3 vezes e perdeu 97 vezes, o saldo foi de -46u.e.

Existem outros tipos de apostas, por exemplo, para 4 números com um coeficiente de 1: 8, aqueles que desejam podem experimentar por conta própria. Como você pode imaginar, todas as probabilidades são projetadas para que o jogador fique no vermelho. Parece tentador colocar 1ye no número para ganhar até 35ue. Mas a quantia vencedora aumenta em 35 vezes e a chance de ganhar diminui em 38 vezes - o saldo final ainda será a favor do cassino.

Lotto 6 de 45

A próxima coisa que é interessante verificar é a loteria. O princípio do jogo é bastante simples - há 45 bolas no tambor, 6 delas caem aleatoriamente. O preço do ingresso, segundo o site Gosloto, é de 100 rublos, e o prêmio depende do número de bolas adivinhadas. A ordem aproximada dos ganhos é a seguinte: 2 bolas adivinhadas dão uma vitória de 100r, 3 bolas adivinhadas dão 300r, 4 bolas - 3000r, 5 bolas - 300.000r e 6 bolas - um super prêmio de cerca de 10.000.000r.

Primeiro, escreva um programa para jogar bolas e comparar o resultado:

 def lottery(values): balls = range(1, 45+1) b1 = balls.pop(random.randint(0, len(balls)-1)) b2 = balls.pop(random.randint(0, len(balls)-1)) b3 = balls.pop(random.randint(0, len(balls)-1)) b4 = balls.pop(random.randint(0, len(balls)-1)) b5 = balls.pop(random.randint(0, len(balls)-1)) b6 = balls.pop(random.randint(0, len(balls)-1)) s = [b1,b2,b3,b4,b5,b6] res = list(set(s) & set(values)) return len(res) 

Uma bola aleatória "obtém" 6 vezes da matriz de bolas e, em seguida, é determinado o número de elementos da interseção de dois conjuntos. Agora vamos construir um gráfico do ganho total no número de ingressos comprados. Por simplicidade, assumimos que o jogador aposta nos mesmos números.

 money = [] money_total = 0 ticket_price = 100 for p in xrange(N): val = lottery([3,7,12,18,33,28]) if val == 2: money_total += 100 if val == 3: money_total += 300 if val == 4: money_total += 3000 if val == 5: money_total += 300000 if val == 6: money_total += 10000000 money.append(money_total) x = range(0, N) price = map(lambda x: ticket_price*x, x) from matplotlib import pyplot as plt %matplotlib inline plt.plot(price, money) 

Para entender a ordem de grandeza: se você comprar 100 bilhetes (o valor total gasto será 10.000r), isso dará 14 bolas "duplas" e uma "tripla". O ganho total é de cerca de 2000r com 10.000r gastos.

A programação de pagamentos para o valor gasto é quase linear:



Acontece que, se você comprar ingressos em um milhão, o ganho será de 250 mil. O “super prêmio” na simulação nunca caiu, embora teoricamente seja certamente possível. A propósito, como está escrito nas regras, o prêmio total é de 50% dos ingressos vendidos, mas o “super prêmio” nem sempre cai, assim como no cassino, os organizadores, é claro, sempre vencem.

Máquinas caça-níqueis

Eles também trabalham com um princípio (pseudo) aleatório, "pseudo" porque O código neles tem sido programático e não possui mecânica limpa. Os princípios gerais descritos acima para máquinas caça-níqueis também funcionam, e os gráficos provavelmente não serão diferentes; quem desejar pode adicionar a função de simulação por conta própria.

Um bom artigo sobre o design de máquinas de jogos já foi publicado no Geektimes.

Conclusão

Talvez este artigo não tenha aberto a América a muitos, mas nos gráficos é, em princípio, mais visual. Acabou sendo mais interessante comparar uma abordagem psicológica fundamentalmente diferente do jogo. Os ganhos na loteria são potencialmente grandes, mas muito raros. Nos cassinos, a abordagem é o oposto - as apostas são configuradas para que uma pessoa ganhe o mais rápido possível. Condicionalmente, depois de fazer 10 jogos em um cassino, uma pessoa ganha 4 vezes e perde 6 vezes. Isso permite que o jogador não perca o interesse no jogo, mas, em qualquer caso, o saldo geral permanece negativo - uma pessoa ganha muitas vezes, mas também perde um pouco mais .

Talvez isso já seja tão óbvio, mas o artigo é apenas sobre jogos baseados na aleatoriedade, não sobre pôquer, cartas, xadrez, etc. Pode haver uma “estratégia vencedora” nesses jogos aleatórios? Obviamente não, porque nem osso, nem bola, nem bilhetes de loteria têm memória e seu comportamento não depende de iterações anteriores. A propósito, é importante lembrar desse momento - intuitivamente, tendo perdido várias vezes, uma pessoa pode decidir que agora “definitivamente” vencerá. Infelizmente, não há roleta ou dado e eles não sabem o número de tentativas anteriores. Cada jogo começa basicamente com uma lista limpa.

Respondendo à pergunta no título do artigo - é possível ganhar jogos de azar? Como mostra a simulação, em princípio é possível, a teoria da probabilidade admite. Mas não por muito tempo - vale a pena começar a jogar pela 2ª, 3ª, ... Nona vez, pois o saldo diminui. A longo prazo, é impossível ganhar no cassino.

PS: Para quem deseja experimentar, o código-fonte em um arquivo é apresentado sob o spoiler. Pode ser executado no IDE Python online, por exemplo aqui . Para testar a versão européia da roleta em vez da americana, basta mudar de 38 para 37 no código.Esta simulação é bastante básica e não leva em consideração vários fatores adicionais, como a quantidade de dinheiro que um jogador tem ou o limite de apostas em um cassino, aqueles que desejam podem adicionar tudo isso independentemente. Sob o spoiler, você também pode assistir a uma versão em vídeo deste artigo.