Brincadeiras à parte, o tópico é sério, risco de incêndio. Vamos lá Este é o terceiro artigo da série, que discute modelos para estimar a corrente máxima da pista impressa, que em algumas situações é um parâmetro determinante na escolha da espessura das camadas condutoras da placa de circuito impresso.
Em um artigo
anterior , foi dito que a escolha da espessura das camadas de cobre de uma placa de circuito impresso é determinada, em primeiro lugar, pela folga mínima exigida e pela largura mínima do condutor, bem como pela corrente máxima que flui através do condutor. Esses parâmetros podem se contradizer: quanto mais fina a camada condutora, menor o padrão topológico pode ser obtido, mas menor a corrente máxima que o caminho de impressão pode suportar (ceteris paribus, a largura do condutor, a largura da corrente, a frequência da corrente, o dissipador de calor etc.). A energia térmica Q liberada na resistência ôhmica R da pista impressa (calor Joule Q = I
2 Rt, onde I é a força atual, t é o tempo) faz com que sua temperatura aumente em relação ao ambiente, levando ao superaquecimento do próprio condutor e dos componentes relacionados, ou, como último recurso, a sua queima em uma corrente limitadora (corrente de fusão em inglês). A correlação entre a corrente através da faixa de impressão e o aumento da temperatura depende de muitos parâmetros e, em geral, é difícil de imaginar; no entanto, existem fórmulas que nos permitem fazer estimativas preliminares.
Price, Onderdonk e Brooks
Uma das primeiras tentativas foi feita por W.H. Pris (WHPreece). Ele recebeu sua dependência empírica em um experimento de laboratório no qual gradualmente aumentou a corrente através do condutor até que brilha em vermelho. A fórmula Pris relaciona a corrente de brilho com o diâmetro do condutor d para vários materiais:
onde K é uma constante tabular aproximadamente igual a 80 para o cobre. Usando a razão da área do círculo, podemos reescrever esta fórmula para o caso de um condutor de cobre com uma área de seção transversal S:
No experimento Pris, o condutor foi suspenso no ar, ao contrário de um condutor em uma placa de circuito impresso, para a qual as condições do dissipador de calor são completamente diferentes. Mais próximas são as condições do dissipador de calor para os casos de um único condutor de conexão, bem como para alguns casos de soldagem com fio de micro-ondas (quando a composição não é usada para protegê-lo), onde essa fórmula pode fornecer uma boa estimativa para a corrente limitadora.
O aumento aceitável da temperatura da pista de impressão é geralmente considerado entre 10 e 30 ° C. Esse valor pode ser maior dependendo dos parâmetros do projeto, no entanto, em toda a faixa de temperaturas de operação do produto, a temperatura da faixa deve ser menor que a temperatura de transição vítrea do material da placa de circuito impresso (temperatura de transição vítrea inglesa, T
g ) e, ainda mais, a temperatura do cobre. Portanto, a dependência do aumento de temperatura ∆T na corrente I da faixa impressa de largura w e espessura da folha h, útil por Brooks em [1], é útil:
onde C, α, β, γ são constantes, cujos valores para as camadas externa e interna são dados na tabela 1. Deve-se ter em mente que nas camadas externas a espessura da folha é geralmente 20-40 mícrons maior que o valor base devido à pulverização adicional ao criar transição buracos. Além disso, o efeito do acabamento em pranchas sem máscara pode ser significativo. Isso é usado em dispositivos de energia, quando uma solda adicional é soldada na faixa impressa aberta a partir da máscara.
Outra fórmula conhecida para calcular a capacidade de carga atual máxima de um condutor é a fórmula Onderdonk (IMOnderdonk), que contém um parâmetro tão importante quanto o tempo. Relaciona o tempo t da passagem da corrente I através de um condutor de cobre com uma seção transversal S e o aumento de temperatura ∆T em relação à temperatura inicial T
0 :
Como na derivação da fórmula [2] qualquer remoção de calor é excluída, no caso de uma faixa de impressão, essa fórmula é aplicável a um pulso de corrente curto que dura de 1 a 2 segundos. Com o aumento do tempo e a influência da remoção de calor, a precisão da estimativa diminui, diminuindo significativamente a corrente limitadora. Os gráficos de dependência para todas as três fórmulas acima para vários parâmetros da faixa de impressão são mostrados nas Figuras 1 e 2.
É sempre importante considerar as condições experimentais ou premissas analíticas na derivação para entender os limites de aplicabilidade de uma fórmula específica. Nenhuma das fórmulas acima fornecerá uma relação exata e ideal entre a corrente limitadora e a seção transversal necessária do condutor para aplicações reais. O mesmo se aplica às calculadoras simples que podem ser encontradas na Internet (
por exemplo ), porque elas são baseadas nessas ou em fórmulas semelhantes. A influência de condutores e componentes vizinhos como fontes e receptores de calor, radiação, resfriamento ativo ou passivo pode ser levada em consideração somente durante a modelagem termoelétrica em sistemas CAD especializados (como Cadence, ANSYS e outros). No entanto, mesmo neste caso, os resultados da modelagem e do experimento podem variar significativamente. O fato é que a pista de impressão não possui uma seção retangular, mas é próxima do trapezoidal (Fig. 3), e seu valor de largura e condutividade da folha de cobre pode diferir não apenas daqueles calculados pelo modelo, mas também ter alguma dispersão de amostra para amostra, lote lote, fabricante para fabricante, etc. A influência dos desvios da largura aumenta com a sua diminuição. No entanto, os resultados calculados por fórmulas e recomendações dos padrões geralmente representam o pior caso, fornecendo assim uma margem de segurança para o sistema. Se o desenvolvedor precisar otimizar a relação entre a corrente limitadora e a seção transversal necessária da pista impressa, será necessário atingir esse objetivo por meio de modelagem e experiência iterativas.

Efeito de pele
Um aumento na seção transversal da pista impressa reduz proporcionalmente sua resistência ôhmica por unidade de comprimento, o que reduz a perda de calor durante o fluxo de corrente direta. A situação com corrente alternada não é tão simples devido à existência de um efeito de pele (efeito de pele inglês), o que leva ao fato de que a densidade da corrente alternada é distribuída de forma desigual pela seção transversal do condutor, diminuindo exponencialmente a zero da superfície do condutor para o centro. Para conveniência dos cálculos, é utilizado o conceito da seção efetiva do condutor com uma profundidade determinada pela razão:
onde f é a frequência atual, σ é a condutividade do metal, μ é a permeabilidade magnética. A uma profundidade igual a δ, a densidade da corrente se torna e vezes menor que a densidade da corrente na superfície J
S. Matematicamente, a seguinte igualdade aproximada pode ser mostrada para a densidade de corrente J (x, y) no condutor:
Ou seja, para cálculos aproximados, podemos supor que a corrente flua apenas na camada limite do condutor de perímetro l de profundidade δ e com uma distribuição uniforme (Fig. 4).

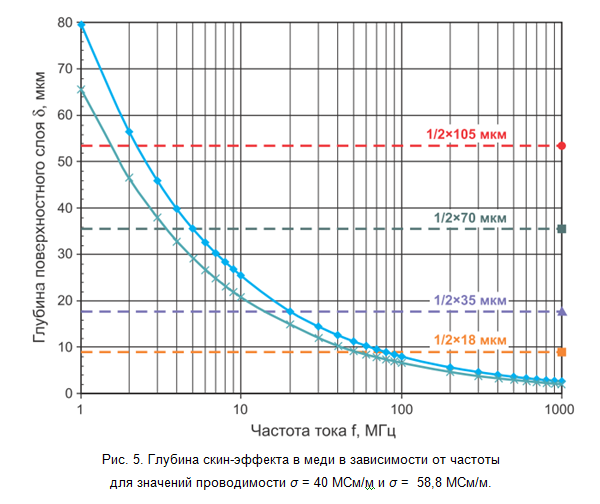
Na estrutura deste modelo simplificado, se a profundidade da camada superficial for menor que a metade da espessura da pista de impressão, a impedância da pista de impressão em uma determinada frequência será determinada por esta seção efetiva, levando a um aumento na resistência ôhmica e uma ligeira diminuição na indutância. Na fig. A Figura 5 mostra a dependência da profundidade da camada superficial da frequência da corrente, levando em consideração a propagação na condutividade do cobre depositado. Pode-se observar que, para as camadas de cobre com 18 μm de espessura, a frequência de corte (acima da qual o efeito da pele desempenha um papel) está na região de 50-70 MHz, e para camadas de 35 μm de espessura, está na região de 15-20 MHz. Observe que em frequências acima de 100 MHz, a profundidade do efeito da pele varia levemente, o que nos permite negligenciar sua dependência da frequência nos cálculos para sinais de alta frequência.
Ao projetar placas de circuito impresso com correntes constantes de vários amperes, é necessário realizar cálculos térmicos para componentes elétricos e condutores. Os modelos apresentados e as relações analíticas nos permitem estimar a corrente máxima de faixas impressas e, com base nisso, selecionar a espessura necessária das camadas de cobre e a topologia dos condutores. Para obter a solução exata, é necessário usar sistemas CAD especializados, embora seja desejável especificar a geometria levando em consideração erros de fabricação e dados de condutividade de cobre recebidos do fabricante de placas de circuito impresso. Eu recomendo a leitura dos
artigos de D. Brooks dedicados a uma análise detalhada dos métodos para estimar a temperatura dos condutores impressos, que fornecem resultados visuais da modelagem dos campos de temperatura.
Literatura
[1] Brooks DG, Adam J. “Rastrear correntes e temperaturas revisadas”, UltraCAD, 2015.
[2] Adam J., Brooks DG, "In Search For Preece and Onderdonk", UltraCAD, 2015.
O artigo foi publicado pela primeira vez na revista Components and Technologies 2018, No. 1. A publicação no Geektimes foi acordada com os editores da revista.