O fracasso da versão elegante original da estrutura do universo

Os oito planetas de nosso sistema solar e nosso sol, observando a escala de seus tamanhos, mas não a escala de suas órbitas. A olho nu, a coisa mais difícil de ver é Mercúrio. Todos os planetas se movem em órbitas elípticas.

As melhores teorias científicas são simples, descomplicadas, prevêem efetivamente os resultados das observações e contêm elegância interior. As equações mais simples de Newton F = ma e Einstein E = mc ² contêm informações pendentes e permitem deduzir muito delas; modelos de quarks e relatividade geral são fáceis de descrever, mas são teorias incrivelmente profundas que controlam as interações de partículas; idéias como supersimetria, teoria da grande unificação e teoria das cordas estendem as simetrias conhecidas pela física a novos níveis. Aplicando novas técnicas matemáticas ao Universo, estamos procurando uma verdade mais profunda na realidade do que nosso nível atual de entendimento.

O modelo original do "Universo elegante", Mysterium Cosmographicum [Segredo do Universo de Kepler], era simétrico, bonito e baseado em matemática, que não havia sido aplicada antes. Mas nossa história de advertência de como acabou sendo um enorme fracasso científico também.


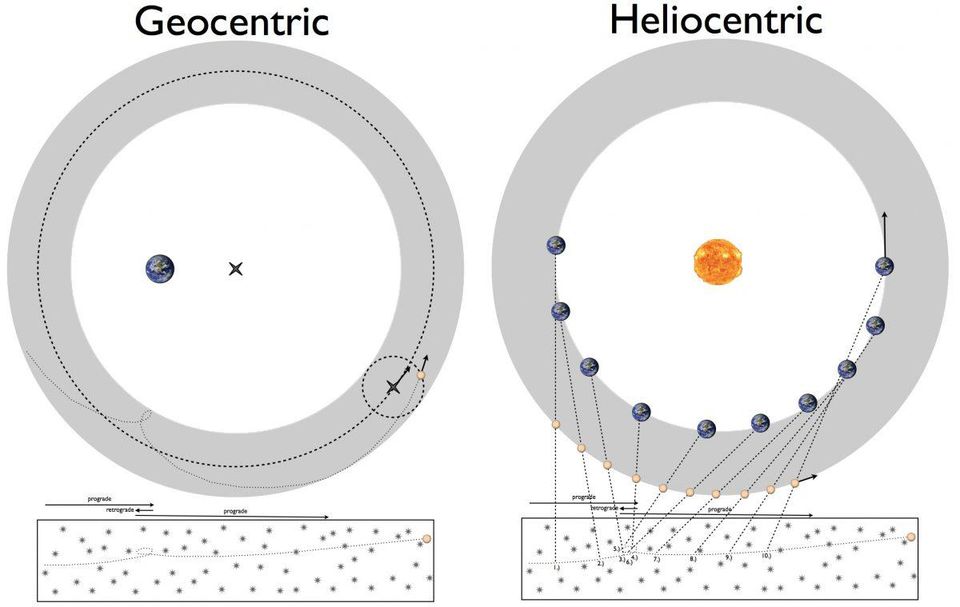Um dos maiores mistérios do século XVI foi como os planetas se movem. Isso pode ser explicado usando o modelo geocêntrico de Ptolomeu (à esquerda) ou o modelo heliocêntrico de Copérnico (à direita). No entanto, nenhum deles conseguiu calcular todos os detalhes com precisão arbitrária.

Antes do Kepler, havia três sistemas principais que descreviam o Universo [o sistema solar em termos daquele tempo]:

1. O modelo de Ptolomeu, no qual a Terra estava imóvel, e tudo girava em torno dela em círculo, usava equantes , adiadores e epiciclos .
2. O modelo copernicano, no qual o Sol estava imóvel e a Terra era um dos seis planetas que o orbitavam, também usava epiciclos.
3. O modelo Tycho Brahe, ou geo-heliocêntrico , no qual o Sol girava em torno da Terra, e todos os outros planetas ao redor do Sol em círculos, também usando epiciclos.

Kepler, criando trabalho científico décadas antes do Galileo, achou que os sistemas heliocêntricos eram promissores, mas precisavam de mais do que apenas círculos. Seu apoio exigia uma estrutura matemática elegante. Em um ataque de gênio, com apenas 24 anos, Kepler publicou uma ideia que considerava a mais bonita de todas.


Kepler decidiu que deveria haver exatamente seis planetas no sistema solar com órbitas definidas com precisão, localizadas em esferas inscritas em poliedros regulares

Como seis planetas giravam em torno do Sol (tudo além de Saturno só seria descoberto 200 anos depois), Kepler decidiu que deveria haver seis órbitas únicas: uma para cada um dos planetas. Mas por que seis? Por que não mais, por que não menos? Por que existem tais distâncias entre eles? A conexão entre órbitas e matemática tornou-se sua idéia de um universo elegante:

Pretendo demonstrar que Deus, criando o universo e posicionando as esferas, tinha em mente cinco poliedros geométricos regulares e limitava os tamanhos, proporções e movimento das esferas a seus tamanhos.

Veja bem, em três dimensões, você pode criar exatamente cinco poliedros a partir de polígonos comuns, nem mais nem menos. Eles foram descobertos pelos gregos antigos há 2000 anos e às vezes são chamados de poliedros platônicos (embora tenham sido descobertos muito antes de Platão). Kepler imaginou um sistema de esferas aninhadas descrito e inscrito em torno de cada um dos poliedros, resultando em seis órbitas esféricas ao longo das quais os planetas se movem.


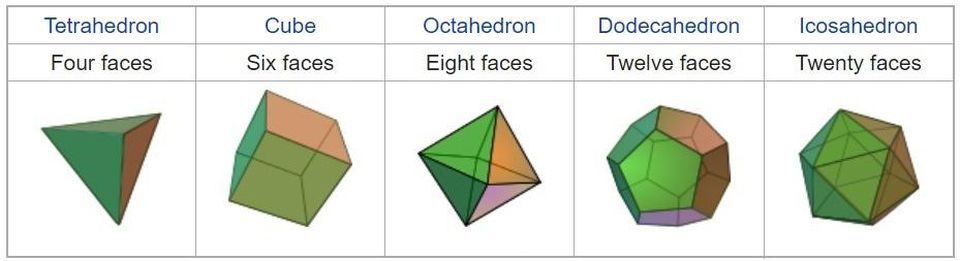Tetraedro, hexaedro (cubo), octaedro, dodecaedro, icosaedro. Cinco poliedros regulares, polígonos compostos e regulares

A esfera de Mercúrio deve ser a mais interna e está localizada dentro do octaedro, um poliedro regular, constituído por oito triângulos equilaterais. Ao seu redor, a esfera de Vênus é descrita - também está inscrita no icosaedro, uma figura de 20 lados composta por triângulos equilaterais. Ao redor, é descrita a esfera da Terra inscrita no dodecaedro, das quais 12 faces são pentágonos. Ao redor, é descrita a esfera de Marte inscrita em um tetraedro: um poliedro tetraédrico com lados em forma de triângulos equilaterais. Ao redor do tetraedro é descrita a esfera de Júpiter, inscrita em um cubo, o polígono resultante. E ao redor é descrita a última esfera, com a órbita de Saturno.


De acordo com a teoria de Kepler, os raios relativos das órbitas dos planetas podem ser facilmente calculados. No entanto, a teoria não nasceu da observação (obviamente a discrepância entre as esferas de Júpiter e Marte com o tetraedro), e Kepler teve que descartá-la.

A ideia de Kepler foi realmente brilhante; com base nisso, foi possível calcular com precisão a proporção dos raios de todas as órbitas. O problema foi revelado ao comparar cálculos com observações. As proporções dos raios calculados das órbitas de Mercúrio e Vênus, Vênus e Terra, Terra e Marte estavam de acordo com a realidade, mas os dois últimos mundos não conseguiram atender aos raios previstos por Kepler. Em particular, o modelo foi refutado pela órbita de Marte, que não correspondia a nenhum círculo. E, embora Kepler tenha continuado a trabalhar nele, e até tenha publicado a segunda edição 20 anos depois, sua contribuição mais notável foi o que a maioria dos cientistas é incapaz de fazer: abandonar sua amada hipótese.


As órbitas dos planetas do sistema solar interno não são inteiramente circulares, mas próximas disso, e a maioria se desvia do círculo de Mercúrio e Marte. Além disso, cometas e asteróides se movem ao longo de elipses, obedecendo ao restante das leis de Kepler, se eles estiverem conectados gravitacionalmente ao Sol.

Mas não foram as esferas aninhadas, mas as elipses que conseguiram prever corretamente o movimento dos planetas. As três leis de Kepler , sobre o movimento de planetas em elipses ao redor do Sol, em áreas iguais descritas por raios por períodos iguais de tempo, e sobre a igualdade das proporções dos quadrados dos períodos de revolução dos planetas e os cubos dos eixos semi-principais de suas órbitas, foram refutados e substituídos por Mysterium Cosmographicum. O sucesso das órbitas elípticas abriu o caminho para a lei da gravitação universal de Newton e gerou a astrofísica. Apesar do amor incondicional de Kepler pela idéia mais brilhante, o universo foi melhor descrito por um modelo menos elegante. Tendo deixado de lado suas esperanças e deixando os dados experimentais se comportarem ainda mais, ele foi capaz de alcançar avanços que a mente menos talentosa não perceberia.


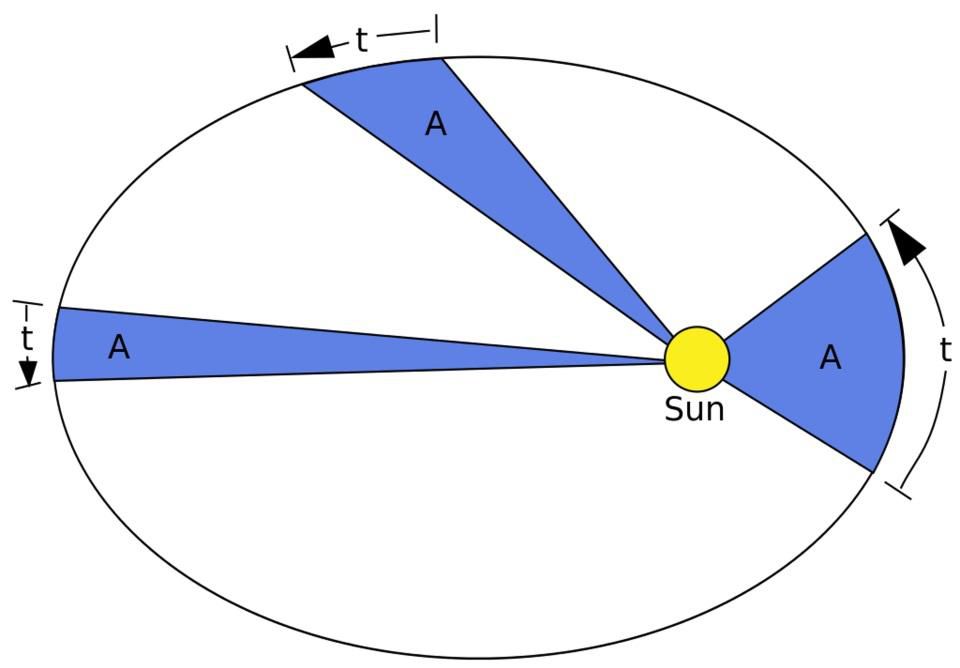As três leis de Kepler se aplicam a qualquer sistema gravitacional e também ao sistema solar.

Na física, há uma tentação de sucumbir ao reducionismo: descrever o maior número possível de fenômenos com o mínimo de meios possível. A idéia da existência de uma teoria de tudo, a única teoria capaz de prever e descrever tudo o que pode ser descrito ou previsto no Universo com a maior precisão possível, é o sonho e o objetivo final de muitos cientistas. No entanto, não há garantia de que esse sonho possa se realizar em princípio. Como escreveu o famoso físico Lincoln Wulfenstein:

A lição de Kepler não é que devemos nos abster de levantar questões aparentemente fundamentais; a lição é que não somos dados para descobrir se há respostas simples para eles e onde eles podem ser encontrados.

Elegância, beleza e reducionismo podem abrir oportunidades incríveis para previsões bem-sucedidas de novos fenômenos físicos, mas não há garantia de que essas previsões se tornem realidade. Fazendo um novo avanço na ciência fundamental, muitos sonhos compartilham nossos sonhos e esperanças de abordar a teoria unificadora de tudo com a ajuda da beleza matemática e da simetria adicional, mas ninguém os garante. Que estejamos todos tão abertos ao fato de que recebemos os dados, como Kepler, e podemos segui-los, não importa para onde eles nos levem.