Em nosso blog sobre Habré, publicamos traduções adaptadas de materiais do blog The Financial Hacker, dedicadas a questões de criação de estratégias de negociação na bolsa. Discutimos anteriormente a
busca por ineficiências do mercado , a criação de
modelos de estratégias de negociação e os
princípios de sua programação . Hoje vamos
nos concentrar no uso de abordagens de aprendizado de máquina para melhorar a eficiência dos sistemas de negociação.
O primeiro computador a vencer o Campeonato Mundial de Xadrez foi o Deep Blue. Isso foi em 1996, e outros vinte anos se passaram antes que outro programa, Alpha Go, conseguisse derrotar o melhor jogador de Go. Deep Blue era um sistema orientado a modelos com regras de xadrez embutidas. AplhaGo é um sistema de mineração de dados, uma rede neural profunda, treinada usando milhares de jogos no Go. Ou seja, para dar um passo nas vitórias sobre as pessoas que são campeãs no xadrez, para dominar os melhores jogadores de Go, era necessário não um pedaço de ferro aprimorado, mas uma inovação no campo do software.
No artigo atual, consideraremos a aplicação da abordagem de mineração de dados para criar estratégias de negociação. Esse método não leva em consideração os mecanismos de mercado, simplesmente verifica as curvas de preços e outras fontes de dados para procurar padrões preditivos. O aprendizado de máquina ou "inteligência artificial" nem sempre é necessário para isso. Pelo contrário, muitas vezes, os métodos mais populares e lucrativos de mineração de dados funcionam sem frescuras na forma de redes neurais ou suporte a métodos vetoriais.
Princípios de aprendizado de máquina
O algoritmo treinado é alimentado com amostras de dados, geralmente extraídas de alguma forma a partir dos preços de câmbio históricos. Cada amostra consiste em n variáveis x1 ... xn, que geralmente são chamadas de preditores, funções, sinais ou, mais simplesmente, dados de entrada. Esses preditores podem ser os preços das últimas n barras no gráfico de preços ou um conjunto de valores de indicadores clássicos ou qualquer outra função da curva de preços (há casos em que pixels individuais do gráfico de preços são usados como preditores para uma rede neural!). Cada amostra também geralmente contém uma determinada variável de destino y, por exemplo, o resultado da próxima transação após analisar a amostra ou o próximo movimento de preço.
Na literatura, y é freqüentemente chamado de rótulo ou objetivo. No processo de aprendizagem, o algoritmo aprende a prever o alvo y com base nos preditores x1 ... xn. O que o sistema “lembra” no processo é armazenado em uma estrutura de dados chamada modelo que é específico para um algoritmo específico (é importante não confundir esse conceito com um modelo financeiro ou estratégia orientada a modelo). Um modelo de aprendizado de máquina pode ser funções com regras de previsão escritas usando o código C gerado pelo processo de aprendizado. Ou poderia ser um conjunto de pesos relacionados à rede neural:
Treinamento: x1 ... xn, y => modelo
Previsão: x1 ... xn, model => y
Preditores, funções ou o que você quiser chamá-los, devem conter informações suficientes para gerar previsões sobre o valor do destino y com uma certa precisão. Eles também devem atender a dois critérios formais. Primeiro, todos os valores do preditor devem estar no mesmo intervalo, por exemplo, -1 ... +1 (para a maioria dos algoritmos em R) ou -100 ... +100 (para algoritmos nas linguagens de script Zorro ou TSSB). Portanto, antes de enviar dados para o sistema, você precisa normalizá-los. Em segundo lugar, as amostras devem ser equilibradas, ou seja, distribuídas uniformemente sobre os valores da variável de destino. Ou seja, você deve ter o mesmo número de amostras que levam a um resultado positivo e perder conjuntos. Se esses dois requisitos não forem seguidos, bons resultados não serão bem-sucedidos.
Os algoritmos de regressão geram previsões sobre valores numéricos, como magnitude ou o sinal do próximo movimento de preço. Os algoritmos de classificação prevêem classes quantitativas de amostras, por exemplo, se precedem o lucro ou a perda de fundos. Alguns algoritmos, como redes neurais, árvores de decisão ou métodos de vetores de suporte, podem ser executados nos dois modos.
Também existem algoritmos que podem aprender a extrair amostras de classe sem a necessidade de um destino y. Isso é chamado de aprendizado não supervisionado, em oposição ao aprendizado supervisionado. Em algum lugar entre esses dois métodos está localizado o "aprendizado por reforço", no qual o sistema treina executando simulações com funções especificadas e usa o resultado como um objetivo. Um seguidor do AlphaGo, um sistema chamado AlphaZero, utilizava o aprendizado reforçado, jogando um milhão de jogos de Go sozinho. Em finanças, esses sistemas ou produtos que usam aprendizado não supervisionado são extremamente raros. 99% dos sistemas usam aprendizado supervisionado.
Quaisquer que sejam os sinais que usamos para preditores em finanças, na maioria dos casos, eles conterão muito ruído e poucas informações e, além disso, serão instáveis. Portanto, a previsão financeira é uma das tarefas mais difíceis do aprendizado de máquina. Algoritmos mais complexos aqui alcançam melhores resultados. A seleção de preditores é fundamental para o sucesso. Não necessariamente deve haver muitos deles, pois isso leva a reciclagem e mau funcionamento. Portanto, as estratégias de mineração de dados geralmente usam um algoritmo pré-selecionado que extrai um pequeno número de preditores de um pool maior. Essa seleção preliminar pode ser baseada na correlação entre preditores, seu significado, riqueza de informações ou simplesmente o sucesso / fracasso do uso da suíte de testes. Experimentos práticos com a seleção de alvos podem ser encontrados, por exemplo, no blog
Robot Wealth .
Abaixo está uma lista dos métodos mais populares de mineração de dados usados no campo das finanças.
1. Sopa de indicadores
A maioria dos sistemas de negociação não se baseia em modelos financeiros. Frequentemente, os comerciantes precisam apenas de sinais de negociação gerados por determinados indicadores técnicos, que são filtrados por outros indicadores em combinação com indicadores técnicos adicionais. Ao perguntar a um profissional sobre como essa confusão de indicadores pode levar a algum tipo de lucro, ele geralmente responde algo como: "Acredite em mim, troco minhas mãos e tudo funciona".
E é verdade. Pelo menos algumas vezes. Embora a maioria desses sistemas não seja aprovada no
teste WFA (e alguns simplesmente testam dados históricos), um número surpreendentemente grande desses sistemas funciona e gera lucro. O autor do blog Financial Hacker está envolvido no desenvolvimento de sistemas de negociação personalizados e conta a história de um dos clientes que experimentou sistematicamente os indicadores técnicos até encontrar uma combinação que funcione para certos tipos de ativos. Esse método de tentativa e erro é uma abordagem clássica da mineração de dados. Para obter sucesso, você só precisa dele, sorte e muito dinheiro para testes. Como resultado, às vezes você pode contar com um sistema lucrativo.
2. Padrões de Candlestick
Não deve ser confundido com os padrões de velas existentes há centenas de anos. O equivalente moderno dessa abordagem é o comércio baseado em movimentos de preços. Você também analisa os indicadores aberto, alto, baixo e fechado para cada vela no gráfico. Mas agora você está usando a mineração de dados para analisar as velas da curva de preços e destacar padrões que podem ser usados para gerar previsões sobre a direção do movimento dos preços no futuro.
Existem pacotes de software completos para esse fim. Eles procuram padrões rentáveis em termos de critérios definidos pelo usuário e os utilizam para criar uma função de detecção de padrões. Tudo isso pode ser algo como isto:
int detect(double* sig) { if(sig[1]<sig[2] && sig[4]<sig[0] && sig[0]<sig[5] && sig[5]<sig[3] && sig[10]<sig[11] && sig[11]<sig[7] && sig[7]<sig[8] && sig[8]<sig[9] && sig[9]<sig[6]) return 1; if(sig[4]<sig[1] && sig[1]<sig[2] && sig[2]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[7]<sig[8] && sig[10]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && eqF(sig[4]-sig[5]) && sig[5]<sig[2] && sig[2]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; if(sig[1]<sig[4] && sig[4]<sig[5] && sig[5]<sig[2] && sig[2]<sig[0] && sig[0]<sig[3] && sig[7]<sig[8] && sig[10]<sig[11] && sig[11]<sig[9] && sig[9]<sig[6]) return 1; if(sig[1]<sig[2] && sig[4]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[7]<sig[8] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9]) return 1; .... return 0; }
Essa função C retorna 1 quando o sinal corresponde a um dos padrões, caso contrário, retorna 0. O código longo parece sugerir que essa não é a maneira mais rápida de procurar padrões. É melhor usar uma abordagem na qual a função de detecção não precise ser exportada, mas pode classificar os sinais por sua importância e classificá-los. Um exemplo desse sistema pode ser encontrado
no link .
O comércio a um preço pode funcionar? Como no caso anterior, esse método não se baseia em nenhum modelo financeiro racional. Ao mesmo tempo, todos entendem que realmente certos eventos no mercado podem afetar seus participantes, como resultado dos quais surgem padrões preditivos de curto prazo. Mas o número de tais padrões não pode ser grande se você estudar apenas a sequência de várias velas consecutivas no gráfico. Você precisará comparar o resultado com os dados das velas, que não estão próximas, mas, pelo contrário, são selecionadas aleatoriamente por um período mais longo. Nesse caso, você obterá um número quase ilimitado de padrões - e romperá com sucesso os conceitos de realidade e racionalidade. É difícil imaginar como o preço futuro pode ser previsto com base em alguns de seus valores na semana passada. Apesar disso, muitos comerciantes trabalham nessa direção.
3. Regressão linear
Uma base simples para muitos algoritmos complexos de aprendizado de máquina: prever a variável de destino y usando uma combinação linear de preditores x1 ... xn.

Probabilidades - este é o modelo. Eles são calculados para minimizar a soma dos desvios quadráticos entre os valores reais de y, os valores de treinamento e os y previstos de acordo com a fórmula:

Para amostras distribuídas normalmente, a minimização é possível usando operações de matriz, portanto, não são necessárias iterações. No caso em que n = 1 - com apenas um preditor x, a fórmula de regressão é reduzida para:
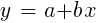
- isto é, antes de uma regressão linear simples, e quando n> 1, a regressão linear será multivariada. A regressão linear simples está disponível na maioria das plataformas de negociação, por exemplo, o indicador
LinReg no TA-Lib. Quando y = preço ex = tempo, ele pode ser usado como uma alternativa às médias móveis. Na plataforma R, essa regressão é implementada pela função de entrega padrão lm (..). Também pode ser representado por regressão polinomial. Como no caso mais simples, aqui usamos uma variável preditiva x, mas também seus graus quadrado e subsequente, então xn == xn:
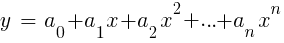
Se n = 2 ou n = 3, a regressão polinomial é frequentemente usada para prever o próximo preço médio dos preços suavizados das últimas barras. Para a regressão polinomial, a função polyfit do MatLab, R, Zorro e muitas outras plataformas pode ser usada.
4. Perceptron
Muitas vezes, é chamada de rede neural com apenas um neurônio. De fato, o perceptron é uma função de regressão, como descrito acima, mas com um resultado binário, como resultado do qual é chamado de
regressão logística . Embora, em geral, isso não seja uma regressão, mas um algoritmo de classificação. Por exemplo, a função de aviso (PERCEPTRON, ...) da estrutura Zorro gera código C que retorna 100 ou -100 dependendo se o resultado previsto é limiar ou não:
int predict(double* sig) { if(-27.99*sig[0] + 1.24*sig[1] - 3.54*sig[2] > -21.50) return 100; else return -100; }
Como você pode ver, a matriz sig é equivalente às funções xn na fórmula de regressão, e os coeficientes a são os fatores digitais.
5. Redes neurais
A regressão linear ou logística pode resolver apenas problemas lineares. Ao mesmo tempo, as tarefas de negociação geralmente não se enquadram nessa categoria. Um exemplo famoso é a previsão da saída de uma função XOR simples. Isso também inclui a previsão de lucro das transações. Uma rede neural artificial (RNA) pode resolver problemas não lineares. Este é um conjunto de perceptrons que estão conectados a uma matriz de diferentes níveis. Cada perceptron é um neurônio da rede. Sua saída se torna entrada para outros neurônios do seguinte nível:
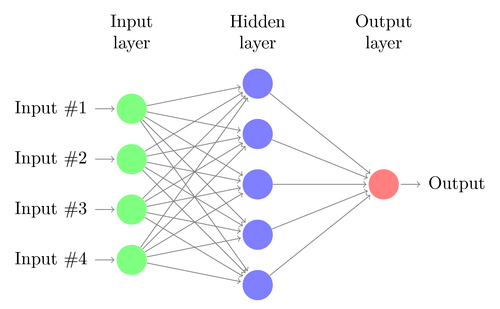
Como o perceptron, a rede neural é treinada determinando coeficientes que minimizam o erro entre a previsão e o alvo na amostra. Isso requer um processo de aproximação, geralmente com a propagação reversa do erro da saída para a entrada com a otimização dos pesos ao longo do caminho. Este processo tem duas limitações. Primeiro, a saída dos neurônios deve ser uma função continuamente diferenciável, em vez de um limiar simples para o perceptron. Em segundo lugar, a rede não deve ser muito profunda - a presença de um grande número de níveis ocultos de neurônios entre os dados de entrada e saída apenas prejudica. Essa segunda limitação limita a complexidade dos problemas que uma rede neural padrão pode resolver.
Ao usar redes neurais para prever transações, você terá muitos parâmetros que podem ser manipulados, os quais, se feitos incorretamente, podem resultar na aparência do viés de seleção:
- número de níveis ocultos;
- o número de neurônios em cada nível oculto;
- o número de ciclos de retropropagação - épocas;
- grau de treinamento, largura da etapa da época;
- momento, fator de inércia para adaptação dos pesos;
- função de ativação.
A função de ativação emula o limiar de perceptron. Para propagação de retorno, você precisa de uma função constantemente diferenciável que gere uma etapa suave para um determinado valor de x. Normalmente, funções sigmóides, tanh ou softmax são usadas para isso. Às vezes, é usada uma função linear que retorna a soma ponderada de todos os dados de entrada. Nesse caso, a rede pode ser usada para regressão, previsão de valores numéricos em vez de saída binária.
As redes neurais estão incluídas na entrega de pacotes padrão do R (por exemplo, nnet é uma rede com um nível oculto), assim como em muitos outros pacotes (como RSNNS e FCNN4R).
6. Aprendizagem profunda
Os métodos de aprendizado profundo usam redes neurais com muitos níveis ocultos e milhares de neurônios que não podem ser efetivamente treinados usando propagação simples das costas. Nos últimos anos, vários métodos se tornaram populares para o treinamento de redes tão grandes. Eles geralmente envolvem pré-treinamento de níveis ocultos de neurônios para aumentar a eficácia do aprendizado básico.
A Máquina de Boltzmann Restrita (RBM) é um algoritmo de classificação não controlado com uma estrutura de rede especial na qual não há conexões entre neurônios ocultos. O Sparse Auto Encoder (SAE) usa a estrutura de rede usual, mas pré-treina os níveis ocultos de uma maneira específica, reproduzindo sinais de entrada nos níveis de saída com o mínimo de conexões ativas possível. Esses métodos permitem implementar redes muito complexas para resolver problemas de aprendizado muito complexos. Por exemplo, a tarefa de derrotar a melhor pessoa jogando Go.
As redes de aprendizado profundo estão incluídas nos pacotes deepnet e darch para R. Deepnet inclui o codificador automático e darch inclui a máquina Boltzmann. Abaixo está um exemplo de código que usa deepnet com três níveis ocultos para processar sinais de negociação por meio da função neor () da estrutura Zorro:
library('deepnet', quietly = T) library('caret', quietly = T) # called by Zorro for training neural.train = function(model,XY) { XY <- as.matrix(XY) X <- XY[,-ncol(XY)] # predictors Y <- XY[,ncol(XY)] # target Y <- ifelse(Y > 0,1,0) # convert -1..1 to 0..1 Models[[model]] <<- sae.dnn.train(X,Y, hidden = c(50,100,50), activationfun = "tanh", learningrate = 0.5, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 100, batchsize = 100, hidden_dropout = 0, visible_dropout = 0) } # called by Zorro for prediction neural.predict = function(model,X) { if(is.vector(X)) X <- t(X) # transpose horizontal vector return(nn.predict(Models[[model]],X)) } # called by Zorro for saving the models neural.save = function(name) { save(Models,file=name) # save trained models } # called by Zorro for initialization neural.init = function() { set.seed(365) Models <<- vector("list") } # quick OOS test for experimenting with the settings Test = function() { neural.init() XY <<- read.csv('C:/Project/Zorro/Data/signals0.csv',header = F) splits <- nrow(XY)*0.8 XY.tr <<- head(XY,splits) # training set XY.ts <<- tail(XY,-splits) # test set neural.train(1,XY.tr) X <<- XY.ts[,-ncol(XY.ts)] Y <<- XY.ts[,ncol(XY.ts)] Y.ob <<- ifelse(Y > 0,1,0) Y <<- neural.predict(1,X) Y.pr <<- ifelse(Y > 0.5,1,0) confusionMatrix(Y.pr,Y.ob) # display prediction accuracy }
7. Vetores de suporte
Como nas redes neurais, o método do vetor de suporte é outra extensão da regressão linear. Se você olhar para a fórmula de regressão novamente:

Então, podemos interpretar as funções xn como as coordenadas de um espaço n-dimensional. Definir a variável de destino y com um valor fixo determinará o plano nesse espaço - será chamado de hiperplano, porque na verdade terá dois (até n-1) tamanhos. O hiperplano separa as amostras com y> 0 daquelas onde y <0. Os coeficientes an podem ser calculados como o caminho que separa o plano das amostras mais próximas - seus vetores de suporte, daí o nome do algoritmo. Assim, obtemos um classificador binário com a separação ideal de amostras vencedoras e perdedoras.
Problema: geralmente essas amostras não podem ser divididas linearmente - elas são agrupadas aleatoriamente em um espaço de função. É impossível traçar um plano suave entre as opções vencedoras e perdedoras; se isso puder ser feito, métodos simples como a análise discriminante linear podem ser usados para calculá-lo. Mas, no caso geral, você pode usar o truque: adicione mais tamanhos ao espaço. Nesse caso, o algoritmo do vetor de suporte poderá gerar mais parâmetros com uma função nuclear que combina dois preditores - semelhante à transição da regressão simples para o polinômio. Quanto mais tamanhos você adicionar, mais fácil será dividir as amostras com um hiperplano. Em seguida, pode ser convertido novamente no espaço n-dimensional original.
Como redes neurais, vetores de referência podem ser usados não apenas para classificação, mas também para regressão. Eles também oferecem várias opções para otimização e possível reciclagem:
- Função do kernel - o kernel RBF (função de base radial, kernel simétrico) é normalmente usado, mas outros kernels podem ser selecionados, por exemplo, sigmóide, polinomial e linear.
- Gama - largura do núcleo RBF.
- Parâmetro de custo C, “penalidade” por classificações incorretas de amostras de treinamento.
A biblioteca libsvm é frequentemente usada, disponível no pacote e1071 para R.
8. Algoritmo de k-vizinhos mais próximos
Comparado com o pesado RNA e SVM, este é um algoritmo simples e agradável, com uma propriedade exclusiva: ele não precisa ser treinado. As amostras serão o modelo. Esse algoritmo pode ser usado para um sistema de negociação que está sendo constantemente treinado, adicionando novas amostras. Este algoritmo calcula as distâncias no espaço de funções do valor atual até as amostras k-mais próximas. A distância no espaço n-dimensional entre os dois conjuntos (x1 ... xn) e (y1 ... yn) é calculada pela fórmula:
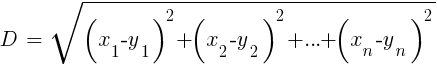
O algoritmo simplesmente prediz o alvo a partir da média de k variáveis-alvo das amostras mais próximas, ponderadas pelas distâncias de retorno. Pode ser usado para classificação e regressão. Para prever os vizinhos mais próximos, você pode chamar a função knn em R ou escrever o código C para esse fim.
9. meios K
Este é um algoritmo de aproximação para classificação não controlada. É um pouco semelhante ao algoritmo anterior. Para classificar amostras, o algoritmo primeiro coloca k pontos aleatórios no espaço de funções. Em seguida, ele atribui a um desses pontos todas as amostras com a menor distância. Então o ponto muda para o meio desses valores mais próximos. Isso gera novas ligações de amostra, pois algumas delas agora estarão mais próximas de outros pontos. O processo é repetido até que a referência novamente, como resultado do deslocamento dos pontos, pare, ou seja, até que cada ponto seja médio para as amostras mais próximas. Agora, temos k classes de amostra, cada uma localizada próxima a um ponto-k.
Esse algoritmo simples pode produzir resultados surpreendentemente bons. Em R, a função kmeans é usada para implementá-la; um exemplo do algoritmo pode ser encontrado
no link .
10. Naive Bayes
Esse algoritmo usa o teorema bayesiano para classificar amostras de funções não numéricas (eventos), como os padrões de vela mencionados acima. Suponha que o evento X (por exemplo, o parâmetro Open da barra anterior abaixo do parâmetro Open da barra atual) apareça em 80% das amostras vencedoras. Então, qual será a probabilidade de ganhar a amostra na presença do evento X nela? Isso não é 0,8 como você imagina. Essa probabilidade é calculada pela fórmula:
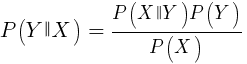
P (Y | X) é a probabilidade de que o evento Y (lucro) ocorra em todas as amostras que contêm o evento X (em nosso exemplo, Open (1) <Open (0)). De acordo com a fórmula, é igual à probabilidade de ocorrência do evento X em todas as amostras vencedoras (no nosso caso, 0,8), multiplicada pela probabilidade Y em todas as amostras (aproximadamente 0,5 se você seguir as dicas para balancear amostras) e dividida pela probabilidade de ocorrência de X em todas as amostras.
Se somos ingênuos e assumimos que todos os eventos de X são independentes um do outro, podemos calcular a probabilidade total de que a amostra estará ganhando simplesmente multiplicando as probabilidades P (X | vencedoras) de cada evento X. Chegamos à seguinte fórmula:
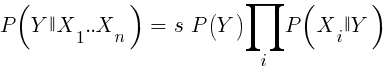
Com fator de escala s. Para que uma fórmula funcione, as funções devem ser escolhidas de forma a serem tão independentes quanto possível. Isso será um obstáculo ao uso de Bayes ingênuo para negociação. Por exemplo, dois eventos Close (1) <Close (0) e Open (1) <Open (0) provavelmente não são independentes um do outro. Preditores numéricos podem ser convertidos em eventos dividindo o número em intervalos separados. Naive Bayes está disponível no pacote e1071 para R.
11. Árvores de decisão e regressão
Tais árvores preveem o resultado de valores numéricos com base em uma cadeia de decisão no formato sim / não na estrutura dos galhos das árvores. Cada decisão representa a presença ou ausência de eventos (no caso de valores não numéricos) ou a comparação de valores com um limite fixo. Uma função típica da árvore, gerada, por exemplo, pela estrutura Zorro, tem a seguinte aparência:
int tree(double* sig) { if(sig[1] <= 12.938) { if(sig[0] <= 0.953) return -70; else { if(sig[2] <= 43) return 25; else { if(sig[3] <= 0.962) return -67; else return 15; } } } else { if(sig[3] <= 0.732) return -71; else { if(sig[1] > 30.61) return 27; else { if(sig[2] > 46) return 80; else return -62; } } } }
Como essa árvore é obtida de um conjunto de amostras? Pode haver vários métodos para isso, incluindo
a entropia informacional de Shannon .
As árvores de decisão podem ser amplamente utilizadas. Por exemplo, eles são adequados para gerar previsões mais precisas do que as obtidas com redes neurais ou vetores de referência. No entanto, esta não é uma solução universal. O algoritmo mais conhecido desse tipo é C5.0, disponível no pacote C50 para R.
Para melhorar ainda mais a qualidade das previsões, você pode usar conjuntos de árvores - elas são chamadas de floresta aleatória. Esse algoritmo está disponível nos pacotes R chamados randomForest, ranger e Rborist.
Conclusão
Existem muitos métodos de mineração de dados e aprendizado de máquina. A questão crítica aqui é a seguinte: quais são as melhores estratégias baseadas em modelo ou de aprendizado de máquina? Não há dúvida de que o aprendizado de máquina tem várias vantagens. Por exemplo, você não precisa se preocupar com a microestrutura do mercado, a economia, levar em consideração a filosofia dos participantes do mercado ou outras coisas semelhantes. Você pode se concentrar em matemática pura. O aprendizado de máquina é uma maneira muito mais elegante e atraente de criar sistemas de negociação. Por seu lado, todas as vantagens, exceto uma - além das histórias nos fóruns dos traders, o sucesso desse método nas negociações reais é difícil de rastrear.
Quase toda semana, novos artigos são publicados sobre negociação usando o aprendizado de máquina. Esses materiais devem ser tomados com uma quantidade razoável de ceticismo. Alguns autores afirmam taxas fantásticas de ganho de 70%, 80% ou até 85%. No entanto, poucas pessoas dizem que você pode perder dinheiro, mesmo que as previsões estejam ganhando. Uma precisão de 85% geralmente se traduz em um indicador de rentabilidade acima de 5 - se tudo fosse tão simples, os criadores desse sistema já se tornariam bilionários. No entanto, por algum motivo, a reprodução dos mesmos resultados simplesmente repetindo os métodos descritos nos artigos falha.
Comparado aos sistemas baseados em modelo, existem muito poucos sistemas de aprendizado de máquina bem-sucedidos. Por exemplo, eles raramente são usados por fundos de hedge bem-sucedidos. Talvez no futuro, quando o poder da computação se tornar ainda mais acessível, algo mudará, mas, por enquanto, os algoritmos de aprendizado profundo continuam sendo mais um hobby interessante para os geeks do que uma ferramenta de fazer dinheiro na bolsa.
Outros materiais relacionados ao mercado financeiro e de ações da ITI Capital :