Para verificar as equações de Einstein, você precisa chutar um buraco negro

Duas equipes de pesquisadores fizeram progressos significativos ao provar a hipótese de estabilidade dos buracos negros, o teste matemático mais importante da Teoria Geral da Relatividade de Einstein.

Em novembro de 1915, em uma palestra na Academia Prussiana de Ciências, Albert Einstein descreveu uma idéia que virou a humanidade ao redor do universo. Em vez de fixar a geometria do espaço e do tempo, Einstein explicou que vivemos em uma realidade quadridimensional chamada espaço-tempo, cuja forma flutua em resposta à matéria e energia.

Einstein descreveu essa importante idéia em detalhes em várias equações chamadas " equações de Einstein " (ou equações do campo gravitacional) que formam o núcleo de seu GTR. Essa teoria foi confirmada por todos os testes experimentais aos quais foi submetida no século seguinte.

E embora a teoria de Einstein pareça descrever o mundo observado, a matemática subjacente permanece em grande parte misteriosa. Os matemáticos foram capazes de fornecer muito pouca evidência sobre as próprias equações. Sabemos que eles funcionam, mas não podemos dizer exatamente o porquê. Até Einstein teve que voltar às aproximações, e não às soluções exatas, para ver o Universo através das lentes que ele criou.

Mas, no ano passado, os matemáticos trouxeram a matemática do GR para um foco mais claro. Dois grupos apresentaram soluções relacionadas a um importante problema no GR, conhecido como hipótese de estabilidade do buraco negro. O trabalho deles prova que as equações de Einstein correspondem à intuição física para o comportamento do espaço-tempo: se você aplicar uma perturbação acentuada, ela sobressairá como geléia e depois se acalmará em um estado estável, a partir do qual tudo começou.

“Se as decisões fossem instáveis, isso significaria que não são físicas. Seria um fantasma matemático que existe na matemática, mas não importa do ponto de vista da física ”, disse Sergiu Kleinerman , matemático da Universidade de Princeton, e o autor, juntamente com Jeremy Szeftel , de um dos dois resultados .

Para completar as provas, os matemáticos precisavam resolver a complexidade básica das equações de Einstein. Para descrever a evolução da forma espaço-tempo, você precisa de um sistema de coordenadas - algo como linhas de latitude e longitude - informando onde estão alguns pontos. E no espaço-tempo é muito difícil encontrar um sistema de coordenadas que funcione em qualquer lugar.

Agite o buraco negro

Como você sabe, o GR descreve o espaço-tempo como algo parecido com uma folha de borracha. Na ausência de matéria, a folha é plana. Comece jogando bolas nele - estrelas e planetas - e a folha se deformará. Bolas rolam uma em direção à outra. Quando os objetos se movem, a forma da folha de borracha também muda em resposta.

As equações de Einstein descrevem a evolução da forma espaço-tempo. Você lhes fornece informações sobre a curvatura e a energia em cada ponto, e elas fornecem a forma do espaço-tempo no futuro. Nesse sentido, as equações de Einstein são semelhantes a qualquer equação que simule um fenômeno físico: aqui a bola está no tempo zero e aqui - depois de cinco segundos.

"Esta é uma versão quantitativa matematicamente precisa da afirmação de que o espaço-tempo é curvado na presença da matéria", disse Peter Hinz, pesquisador do Instituto de Matemática Clay da Universidade da Califórnia em Berkeley, responsável pelo segundo resultado com Andras Vasya.

Em 1916, quase imediatamente após o lançamento do GTR, o físico alemão Karl Schwarzschild encontrou uma solução exata para as equações que descrevem o que sabemos agora pelo nome de um buraco negro (esse termo apareceu apenas cinco décadas depois ). Mais tarde, os físicos encontraram soluções exatas descrevendo um buraco negro rotativo e BH com uma carga elétrica.

E todas essas são decisões exatas que descrevem BH. Se você adicionar pelo menos um segundo BH, a interação de forças se torna tão complicada para a matemática moderna que só lida com ela em casos muito especiais.

No entanto, ainda podemos fazer perguntas importantes sobre esse grupo limitado de soluções. Uma dessas questões surgiu em 1952, como resultado do trabalho do matemático francês Yvonne Choquet-Bruhat. De fato, soa assim: o que acontece se você balançar um buraco negro?


Se você agitar o BH, ele criará ondas gravitacionais. Provar a hipótese de estabilidade é o mesmo que provar que essas ondas se dispersam no vazio, como ondas na superfície de uma lagoa depois que uma pedra cai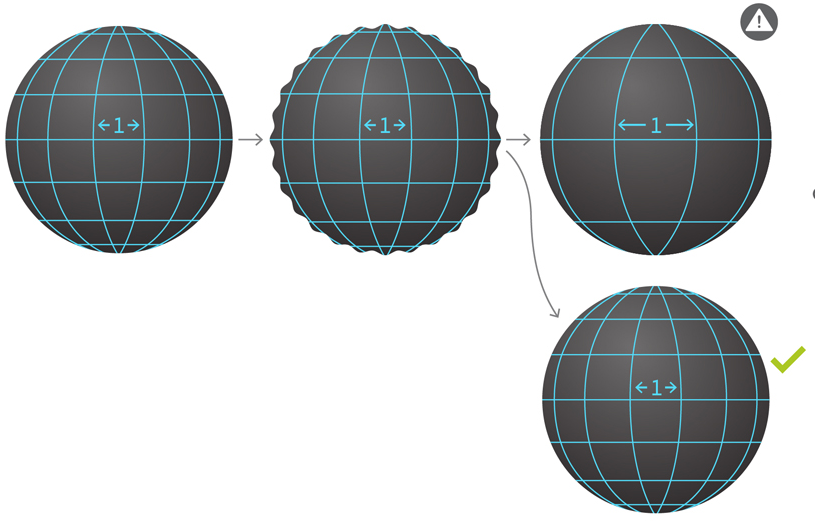


O espaço-tempo muda com o tempo, e a grade usada para medir as ondas amortecidas muda com ela. O modelo determina as alterações na grade e deve ser selecionado corretamente. Suponha que tenhamos um espaço-tempo com uma grade de 1 cm associada a um determinado padrão. Vamos perturbar o espaço-tempo para que as ondas gravitacionais apareçam. Um padrão selecionado incorretamente pode causar alterações nas distâncias da grade e parecerá que as ondas não estão atenuando. O padrão certo é crucial para medir o retorno à sustentabilidade.

Esse problema é conhecido como hipótese de estabilidade de BH. Ela prevê que as soluções para as equações de Einstein serão "estáveis ​​sob perturbações". Informalmente, se você chocar o BH, o espaço também se tornará mais caro e, em toga, ele se acalmará de uma forma que será muito parecida com a que começamos. "De maneira geral, sustentabilidade significa que, se tomarmos soluções especiais e as ofendermos um pouco, mudarmos os dados, a dinâmica final estará muito próxima da solução original", disse Kleinerman.

A chamada "estabilidade" é um teste importante de qualquer teoria física. Para entender isso, seria útil apresentar um exemplo mais familiar que BH.

Imagine uma lagoa. Agora imagine que você revoltou sua superfície jogando uma pedra ali. A lagoa está um pouco preocupada e depois se acalma. Matematicamente, as soluções das equações usadas para descrever a lagoa (neste caso, as equações de Navier-Stokes ) devem descrever esse quadro físico básico. Se a solução original não coincidir com a decisão no futuro distante, você pode se perguntar sobre a exatidão de suas equações.

"Uma equação pode ter quaisquer propriedades, pode ser matematicamente correta, mas se contradizer as expectativas físicas, não poderá estar correta", disse Vasya.


Peter Hinz, matemático da Universidade da Califórnia

Para os matemáticos que trabalham nas equações de Einstein, era mais difícil encontrar provas de estabilidade do que soluções para as próprias equações. Considere o caso de um espaço plano de Minkowski - a mais simples de todas as configurações de espaço-tempo. Essa solução das equações de Einstein foi descoberta em 1908, no contexto da teoria especial anterior da relatividade de Einstein. Mas somente em 1993, os matemáticos foram capazes de provar que, se você abalar o espaço-tempo vazio e plano, então novamente obtém o espaço-tempo plano e vazio. Este resultado, obtido por Kleinermann e Demetrios Christodoulou, é um trabalho reverenciado nessa área.

Uma das principais dificuldades com a prova de estabilidade está associada ao rastreamento do que está acontecendo no espaço-tempo quadridimensional durante a evolução de uma solução. Você precisa de um sistema de coordenadas que permita medir distâncias e determinar pontos no espaço-tempo, como as linhas de latitude e longitude, usadas para determinar uma localização na Terra. Mas não é fácil encontrar um sistema de coordenadas que funcione em todos os pontos do espaço temporal e continue a funcionar quando a forma do espaço-tempo muda.

"Não sabemos como fazer isso, adequado para todos os casos", disse Hinz em um email. "O universo não nos dá um sistema de coordenadas preferido."

Problema de medição

A primeira coisa a entender sobre sistemas de coordenadas é que as pessoas os inventaram. O segundo - nem todo sistema de coordenadas permite definir todos os pontos no espaço.

Tome latitude e longitude: eles podem ser atribuídos arbitrariamente. Os cartógrafos poderiam escolher qualquer linha imaginária como o meridiano principal. E embora a latitude e a longitude ajudem a determinar quase qualquer lugar da Terra, elas não fazem mais sentido nos pólos norte e sul. Se você não soubesse nada sobre a Terra e tivesse apenas leituras de latitude e longitude em suas mãos, poderia concluir incorretamente que algo topologicamente errado está acontecendo nesses pontos.

Essa possibilidade - tirar conclusões incorretas sobre as propriedades do espaço físico devido à inadequação do sistema de coordenadas que o descreve - é a essência do motivo pelo qual é tão difícil provar a estabilidade do espaço-tempo.

"Pode ser que a estabilidade exista, mas usamos coordenadas instáveis ​​e, assim, ignoramos a verdade da estabilidade", disse Michalis Dafermos, matemático da Universidade de Cambridge, especialista em estudos das equações de Einstein.

No contexto da teoria da estabilidade de um buraco negro, qualquer sistema de coordenadas usado deve se desenvolver da mesma maneira que a forma do espaço-tempo - como uma luva confortável que se adapta à mudança da forma da mão. A correspondência entre o sistema de coordenadas e o espaço-tempo deve ser boa no início e permanecer boa por todo o caminho. Se não for assim, duas coisas podem acontecer que interferem nas tentativas de provar a existência de estabilidade.


Sergiu Kleinerman, matemático da Universidade de Princeton

Primeiro, seu sistema de coordenadas pode mudar de forma, o que será interrompido em determinados pontos, assim como a latitude e a longitude param de funcionar nos pólos. Esses pontos são chamados de "singularidades coordenadas" (para distingui-las das singularidades físicas, por exemplo, buracos negros). Esses são pontos indefinidos no sistema de coordenadas que não permitem descrever completamente o desenvolvimento da solução até o fim.

Em segundo lugar, um sistema de coordenadas mal selecionado pode ocultar o fenômeno físico que deve ser medido. Para provar que as soluções das equações de Einstein chegam a um estado calmo após perturbações, os matemáticos precisam monitorar cuidadosamente as ondulações do espaço-tempo causadas por perturbações. Para entender por que isso é necessário, vale a pena voltar novamente à analogia com a lagoa. Uma pedra jogada em um lago gera ondas. A estabilidade a longo prazo da lagoa decorre do fato de que as ondas enfraquecem com o tempo - elas se tornam cada vez menores, até que não haja vestígios de sua presença.

A situação é semelhante ao espaço-tempo. A perturbação causará uma cascata de ondas gravitacionais e, para provar a estabilidade, é necessário provar que essas ondas são atenuadas. E para isso, é necessário um sistema de coordenadas, ou "grade", para medir o tamanho das ondas. A grade correta permite que os matemáticos vejam como as ondas achatam e eventualmente desaparecem para sempre.

"A atenuação precisa ser medida em relação a alguma coisa, e é aí que entra o problema da rede", disse Kleinerman. "Se pegarmos a grade errada, mesmo que a estabilidade esteja presente, isso não pode ser provado, pois a grade não me mostrará atenuação." E se você não calcular a taxa de atenuação das ondas, é impossível provar a estabilidade.

O problema é que, embora o sistema de coordenadas seja extremamente importante, não é óbvio qual sistema escolher. "Há muita liberdade na escolha das condições para essa grade", disse Hinz. "E a maioria das opções acabará errada."

A caminho do objetivo

Uma prova completa da estabilidade dos buracos negros requer prova de que todas as soluções conhecidas das equações de Einstein para BHs (com a rotação do buraco negro dentro de certos limites) permanecem estáveis ​​após perturbações. Entre as soluções conhecidas estão a solução Schwarzschild que descreve o espaço-tempo de uma BH não rotativa e a família de soluções Kerr que descreve a configuração do espaço-tempo na qual não há nada além de uma BH rotativa (e as propriedades desse BH - momento de massa e angular - diferem na família de soluções) .

Ambos os novos resultados avançaram parcialmente para a prova de uma hipótese completa.

Hinz e Washi, em um artigo publicado no arxiv.org em 2016, provaram que os buracos negros de rotação lenta são estáveis. Mas o trabalho deles não abrange as BHs rotativas a uma velocidade maior que um determinado limite.

Além disso, suas evidências têm várias suposições sobre a natureza do espaço-tempo. A hipótese original ocorreu no espaço de Minkowski, que não é apenas plano e vazio, mas também tem um certo tamanho. A prova de Hintz e Vasya ocorre no espaço de Sitter, onde o espaço-tempo com aceleração cresce para fora, como no universo real. Mudar a cena simplifica o problema do ponto de vista técnico, e isso pode ser entendido por analogia: se você atirar uma pedra em uma lagoa em expansão, a expansão esticará as ondas e elas enfraquecerão mais rapidamente do que se a lagoa não se expandisse.

"Estamos vendo um universo com expansão acelerada", disse Hinz. "Isso torna a tarefa um pouco mais fácil, porque esse processo dilui as ondas gravitacionais."

Kleinermann e Scheftel têm uma característica ligeiramente diferente. A prova, cuja primeira parte foi publicada em novembro passado, ocorre no espaço-tempo de Schwarzschild - mais próximo da condição original e mais complexa do problema. Eles provam a estabilidade de uma BH não rotativa, mas não dizem respeito às decisões nas quais ele gira. Além disso, eles provam a estabilidade de BH apenas para uma classe estreita de perturbações - aquelas em que as ondas gravitacionais geradas são simétricas de uma certa maneira.

Ambos os resultados apresentam novas técnicas para selecionar o sistema de coordenadas apropriado. Hinz e Vasi começam com uma solução aproximada de equações com base em um sistema aproximado de coordenadas e aumentam gradualmente a precisão da resposta, até chegarem a soluções exatas e coordenadas com bom comportamento. Kleinerman e Scheftel usam uma abordagem mais geométrica.

Agora as duas equipes estão tentando construir uma prova da hipótese completa com base em seus métodos. Alguns especialistas observadores acreditam que o dia em que dá certo não está longe.

"Eu realmente acredito que agora tudo está no estágio de dificuldades técnicas", disse Dafermos. "Acontece que, para resolver esse problema, novas idéias não são mais necessárias." Ele enfatizou que a prova final pode ser oferecida por qualquer matemático que trabalha no problema no momento.

Por cem anos, as equações de Einstein serviram como uma instrução experimental confiável para o Universo. Agora os matemáticos provavelmente estão se aproximando de demonstrar por que funcionam tão bem.