Determinação da densidade do gás a partir dos resultados da medição de pressão e temperatura com sensores Arduino

1. Introdução

A tarefa de medir os parâmetros de uma mistura de gás é generalizada na indústria e no comércio. O problema de obter informações confiáveis ​​ao medir os parâmetros do estado do meio gasoso e suas características usando meios técnicos é resolvido pelos procedimentos de medição adotados nas normas (MVI), por exemplo, ao medir a vazão e a quantidade de gases usando dispositivos de restrição padrão [1] ou turbina, contadores e contadores de rotações e vórtices [2].

A análise periódica de gases nos permite estabelecer uma correspondência entre a mistura real analisada e seu modelo, segundo o qual os parâmetros físico-químicos do gás são levados em consideração no MVI: a composição da mistura de gases e a densidade do gás em condições padrão.
Além disso, o MVI leva em consideração as características termofísicas do gás: densidade sob condições operacionais (pressão e temperatura do gás em que sua vazão ou volume é medido), viscosidade, fator e fator de compressibilidade.

Os parâmetros do estado do gás medidos em tempo real incluem: pressão (pressão diferencial), temperatura, densidade. Para medir esses parâmetros, respectivamente, são utilizados meios de medição: manômetros (manômetros diferenciais), termômetros, densitômetros. A medição da densidade do meio gasoso pode ser medida por métodos de medição diretos ou indiretos. Os resultados dos métodos de medição direta e indireta dependem do erro dos instrumentos de medição e do erro metodológico. Sob condições de operação, os sinais de informações de medição podem ser afetados por ruído significativo, cujo desvio quadrado médio pode exceder o erro instrumental. Nesse caso, uma tarefa urgente é a filtragem eficaz dos sinais de informações de medição.

Este artigo discute o método de medição indireta da densidade do gás em condições operacionais e padrão usando um filtro Kalman.

Modelo matemático para determinar a densidade do gás

Vamos nos voltar aos clássicos e relembrar a equação de estado de um gás ideal [3]. Nós temos:

1. A equação de Mendeleev-Clapeyron: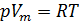

(1)

onde:

- pressão de gás;

- volume molar;

R é a constante universal de gás,

;

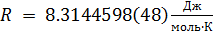
T é a temperatura absoluta, T = 273,16 K.

2. Dois parâmetros medidos:

p - pressão do gás, Pa
t é a temperatura do gás, ° C.

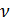
Sabe-se que o volume molar depende do volume de gás V e do número de mols de gás neste volume:

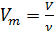
2)

Sabe-se também que

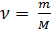
(3)

onde: m é a massa de gás, M é a massa molar de gás.

Dado (2) e (3), reescrevemos (1) na forma:

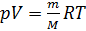
(4)

Como é sabido, a densidade de uma substância

é igual a:

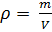
(5)

De (4) e (5) derivamos a equação para a densidade do gás

:

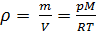
(6)

e introduza a notação para o parâmetro

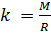
, que depende da massa molar da mistura gasosa:

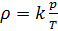
(7)

Se a composição da mistura gasosa não mudar, o parâmetro k é constante.
Portanto, para calcular a densidade do gás, é necessário calcular a massa molar da mistura de gases.

A massa molar de uma mistura de substâncias é definida como a média aritmética da massa molar das frações de massa incluídas na mistura de substâncias individuais.

Tomamos a composição conhecida de substâncias em uma mistura gasosa - no ar, que consiste em:

• 23% em peso de moléculas de oxigênio
• 76% em peso de moléculas de nitrogênio
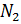
• 1% em peso de átomos de argônio

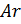
As massas molares dessas substâncias atmosféricas serão respectivamente iguais a:

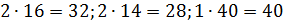
, g / mol.

Calculamos a massa molar do ar como a média aritmética ponderada:



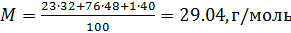
Agora, sabendo o valor da constante

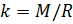
, podemos calcular a densidade do ar de acordo com a fórmula (7), levando em consideração os valores medidos

e t :

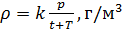
Trazendo a densidade do gás para condições normais e padrão

Na prática, as medições das propriedades dos gases são realizadas em diferentes condições físicas e, para garantir a comparação entre diferentes conjuntos de dados, devem ser estabelecidos conjuntos padrão de condições [4].

Condições padrão de temperatura e pressão são as condições físicas estabelecidas pelo padrão, com as quais as propriedades das substâncias que dependem dessas condições são correlacionadas.

Várias organizações estabelecem suas condições padrão, por exemplo: a União Internacional de Química Pura e Aplicada (IUPAC), estabeleceu a definição de temperatura e pressão padrão (STP) no campo da química: temperatura 0 ° C (273,15 K), pressão absoluta 1 bar (Pa); O Instituto Nacional de Padrões e Tecnologia (NIST) define uma temperatura de 20 ° C (293,15 K) e uma pressão absoluta de 1 atm (101,325 kPa), e esse padrão é chamado temperatura e pressão normais (NTP); A Organização Internacional de Padronização (ISO) estabelece condições padrão para o gás natural (ISO 13443: 1996, confirmado em 2013): temperatura 15,00 ° C e pressão absoluta 101,325 kPa.

Portanto, na indústria e no comércio é necessário indicar condições padrão para temperatura e pressão, com relação às quais os cálculos necessários são feitos.

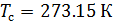
Calculamos a densidade do ar de acordo com a equação (8) sob condições operacionais de temperatura e pressão. De acordo com (6), escrevemos a equação para a densidade do ar em condições padrão: temperatura e pressão absoluta :

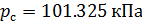
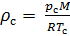
(9)

Fazemos o cálculo da densidade do ar reduzida para condições padrão. Dividimos a equação (9) pela equação (6) e escrevemos essa relação para :

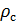
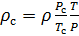
(10)

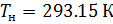
Da mesma forma, obtemos uma equação para calcular a densidade do ar reduzida a condições normais: temperatura e pressão absoluta

:

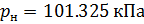
(11)

Nas equações (10) e (11) usamos os valores dos parâmetros do ar , T e P da equação (8) obtida em condições operacionais.

A implementação da pressão e temperatura do canal de medição

Para resolver muitas tarefas de obtenção de informações, dependendo de sua complexidade, é conveniente criar um protótipo de um sistema futuro baseado em uma das plataformas de microcontroladores, como Arduino, Nucleo, Teensy, etc.

O que poderia ser mais fácil? Vamos criar uma plataforma de microcontrolador para resolver um problema específico - criar um sistema para medir pressão e temperatura, gastar menos, possivelmente, fundos e usar todas as vantagens do desenvolvimento de software no ambiente do Arduino Software (IDE).

Para isso, no nível do hardware, precisaremos de componentes:

1. Arduino (Uno, ...) - use como programador;
2. microcontrolador ATmega328P-PU - microcontrolador da futura plataforma;
3. um ressonador de quartzo de 16 MHz e um par de capacitores de cerâmica de 12 a 22 pF cada (de acordo com as recomendações do fabricante);
4. um botão de relógio para redefinir o microcontrolador e um pull-up plus power no pino RESET do resistor de 1 kOhm do microcontrolador;
5. BMP180 - transmissor de temperatura e pressão com interface I2C;
6. conversor de interface TTL / USB;
7. consumíveis - fios, solda, placa de circuito, etc.

Um diagrama esquemático da plataforma, levando em consideração as interfaces necessárias: uma interface serial padrão, I2C, e nada mais, é apresentada na Fig. 1


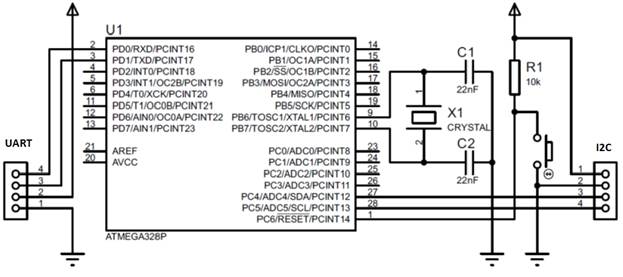Fig. 1 - Diagrama esquemático de uma plataforma de microcontrolador para a implementação de um sistema de medição de pressão e temperatura

Agora vamos considerar os estágios da implementação de nossa tarefa.

1. Primeiro, precisamos de um programador. Conectamos o Arduino (Uno, ...) ao computador. No ambiente do Arduno Software, no menu, vá para Arquivo-> Exemplos-> 11. No ArdunoISP , chegamos ao programador ArduinoISP, que costuramos no Arduino. Primeiro, no menu Ferramentas, selecione respectivamente Placa, Processador, Carregador, Porta. Depois de baixar o programa ArduinoISP na placa, o nosso Arduino se transforma em programador e está pronto para uso para a finalidade a que se destina. Para fazer isso, no ambiente do Arduno Software, no menu Ferramentas , selecione o item Programador: “Arduino como ISP ”.

2. Conecte o microcontrolador escravo ATmega328P via interface SPI ao programador mestre do Arduino (Uno, ...), Fig. 2. Deve-se notar que anteriormente os bits do registro Low Fuse Byte do microcontrolador ATmega328P estavam em um estado não programado. Vá para o ambiente do Arduno Software e, no menu Ferramentas , selecione o item Burn Loader . Piscando o microcontrolador ATmega328P.


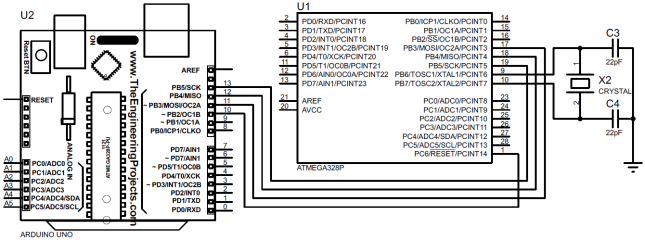Fig. 2 - Esquema de conexão do microcontrolador ao programador

3. Após o firmware bem-sucedido, o microcontrolador ATmega328P está pronto para instalação na plataforma de microcontroladores desenvolvida (Fig. 3), que é programável e também no Arduino completo (Uno, ...). O programa de polling para o transmissor de pressão e temperatura é mostrado na Listagem 1.


Fig. 3 Sistema de medição de pressão e temperatura

Programa Python para filtrar por canais de temperatura e pressão e obter resultados

O programa Python para o método para determinar a densidade do gás a partir de medições de pressão e temperatura é mostrado na Lista 2. As informações do sistema de medição são exibidas em tempo real.


Os resultados do cálculo são apresentados listando e Fig. 4, 5, 6.



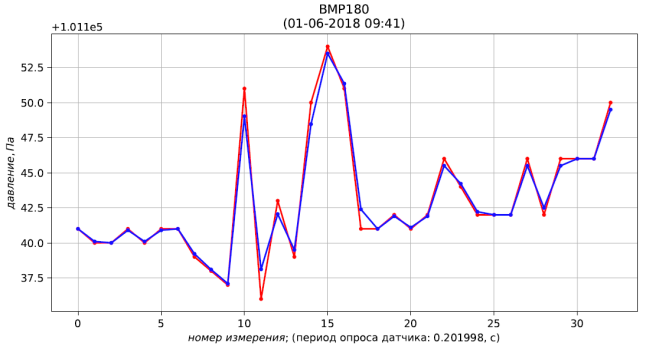Fig. 4 - resultados da medição (vermelha) e filtração (azul) da pressão


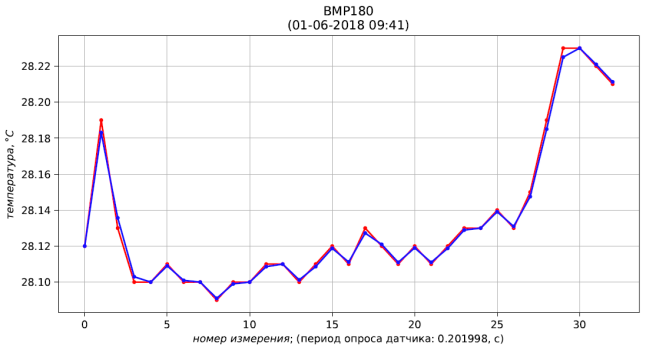Fig. 5 - resultados da medição (vermelho) e filtração (azul) da temperatura


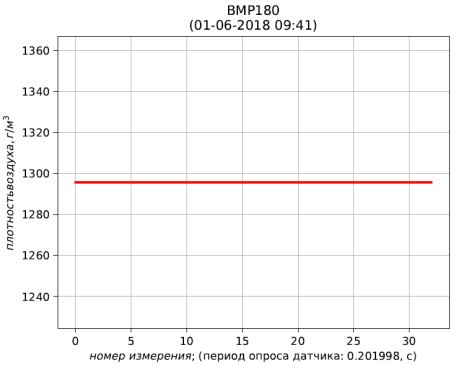Fig. 6 - resultados de cálculo da densidade do ar reduzida para condições padrão (temperatura 273,15 K; pressão absoluta 101,325 kPa)

Conclusões

Uma técnica foi desenvolvida para determinar a densidade do gás a partir de medições de pressão e temperatura usando sensores Arduino e software Python.

Links para fontes de informação

1. GOST 8.586.5-2005. URL
2. GOST R 8.740 - 2011. URL
3. Lei do gás ideal. URL
4. Condições padrão para temperatura e pressão. URL