Tradução de como as máquinas percebem o big data: uma introdução aos algoritmos de cluster .Dê uma olhada na imagem abaixo. Esta é uma coleção de insetos (caracóis não são insetos, mas não encontraremos falhas) de várias formas e tamanhos. Agora divida-os em vários grupos de acordo com o grau de semelhança. Não pega. Comece agrupando aranhas.
Terminou? Embora não exista uma solução "certa" aqui, você deve ter dividido essas criaturas em quatro
grupos . Em um aglomerado há aranhas, no segundo - um par de caracóis, no terceiro - borboletas e no quarto - um trio de abelhas e vespas.
Bem feito, certo? Você provavelmente poderia fazer o mesmo se houvesse o dobro de insetos na imagem. E se você tivesse muito tempo - ou um desejo de entomologia -, provavelmente teria agrupado centenas de insetos.
No entanto, para uma máquina, agrupar dez objetos em grupos significativos não é uma tarefa fácil. Graças a um ramo tão complexo da matemática como a
combinatória , sabemos que 10 insetos são agrupados de 115.975 maneiras. E se houver 20 insetos, o número de opções de agrupamento
excederá 50 trilhões .
Com cem insetos, o número de soluções possíveis será maior que o
número de partículas elementares no Universo conhecido . Quanto mais? Segundo minhas estimativas, cerca de
quinhentos milhões de bilhões de bilhões de vezes mais . Acontece que mais de
quatro milhões de bilhões de soluções do
Google (o
que é o Google? ). E isso é apenas para centenas de objetos.
Quase todas essas combinações serão sem sentido. Apesar do número inimaginável de soluções, você mesmo encontrou rapidamente uma das poucas maneiras úteis de agrupar.
Nós, humanos, temos como certa nossa excelente capacidade de catalogar e entender grandes quantidades de dados. Não importa se é texto ou imagens na tela ou uma sequência de objetos - as pessoas, em geral, compreendem efetivamente os dados provenientes do mundo circundante.
Dado que um aspecto fundamental do desenvolvimento da IA e do aprendizado de máquina é que as máquinas podem entender rapidamente grandes volumes de dados de entrada, como posso melhorar a eficiência do trabalho? Neste artigo, consideraremos três algoritmos de clustering com os quais as máquinas podem compreender rapidamente grandes quantidades de dados. Esta lista está longe de ser completa - existem outros algoritmos - mas já é bem possível começar com ela.
Para cada algoritmo, descreverei quando ele pode ser usado, como funciona e também darei um exemplo com a análise passo a passo. Acredito que, para uma compreensão real do algoritmo, você precisa repetir o trabalho você mesmo. Se você estiver
realmente interessado , perceberá que é melhor executar algoritmos no papel. Ato, ninguém te culpará!
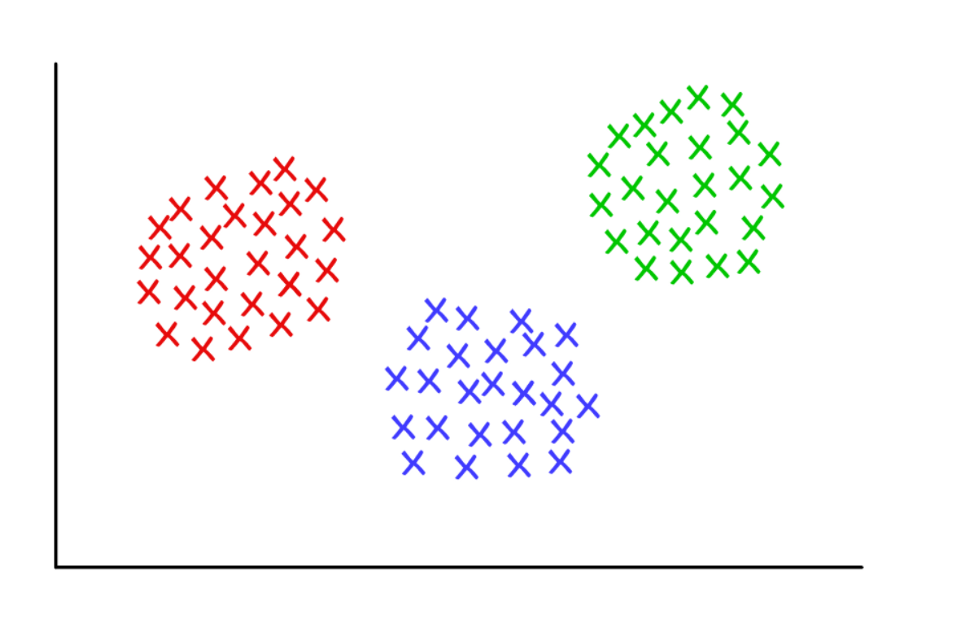Três grupos suspeitosamente limpos com k = 3Cluster K-significa
Usado por:
Quando você entende quantos grupos podem ser obtidos para encontrar
um predeterminado (a priori).
Como funciona:
O algoritmo atribui aleatoriamente cada observação a uma das
k categorias e calcula a
média de cada categoria. Em seguida, ele reatribui cada observação à categoria com a média mais próxima e calcula novamente as médias. O processo é repetido até que sejam necessárias reatribuições.
Exemplo de trabalho:
Pegue um grupo de 12 jogadores e o número de gols marcados por cada um na temporada atual (por exemplo, no intervalo de 3 a 30). Dividimos os jogadores, digamos, em três grupos.
Etapa 1 : você precisa dividir os jogadores aleatoriamente em três grupos e calcular a média de cada um deles.
Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16
Etapa 2 : reatribua cada jogador ao grupo com a média mais próxima. Por exemplo, o jogador A (5 gols) vai para o grupo 2 (média = 9). Então, novamente, calculamos as médias do grupo.
Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21
Repita o passo 2 várias vezes até que os jogadores parem de mudar de grupo. Neste exemplo artificial, isso acontecerá na próxima iteração.
Pare com isso! Você formou três clusters a partir de um conjunto de dados!
Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23
Os agrupamentos devem corresponder à posição dos jogadores em campo - defensores, zagueiros e atacantes. K-significa funciona neste exemplo porque há motivos para acreditar que os dados serão divididos nessas três categorias.
Assim, com base na variação estatística no desempenho, a máquina pode justificar a localização dos jogadores em campo para qualquer esporte coletivo. Isso é útil para análises esportivas, bem como para outras tarefas nas quais a divisão do conjunto de dados em grupos predefinidos ajuda a tirar as conclusões apropriadas.
Existem várias variações do algoritmo descrito. A formação inicial de clusters pode ser realizada de várias maneiras. Examinamos a classificação aleatória dos jogadores em grupos, seguida pelo cálculo das médias. Como resultado, as médias iniciais do grupo são próximas umas das outras, o que aumenta a repetibilidade.
Uma abordagem alternativa é formar grupos que consistem em apenas um jogador e depois agrupá-los nos grupos mais próximos. Os clusters resultantes são mais dependentes do estágio inicial de formação e a repetibilidade em conjuntos de dados com alta variabilidade diminui. Mas com essa abordagem, pode levar menos iterações para concluir o algoritmo, porque menos tempo será gasto na divisão dos grupos.
A desvantagem óbvia do agrupamento k-means é que você precisa adivinhar
antecipadamente quantos clusters você possui. Existem métodos para avaliar a conformidade de um conjunto específico de clusters. Por exemplo, Soma dos quadrados dentro do cluster é uma medida de variabilidade dentro de cada cluster. Quanto "melhores" os agrupamentos, menor a soma total de quadrados intracluster.
Armazenamento em cluster hierárquico
Usado por:
Quando você precisa revelar a relação entre os valores (observações).
Como funciona:
A matriz de distância é calculada na qual o valor da célula (
i, j ) é a métrica da distância entre os valores de
iej . Então, um par dos valores mais próximos é obtido e a média é calculada. Uma nova matriz de distância é criada, os valores emparelhados são combinados em um objeto. Em seguida, um par dos valores mais próximos é obtido dessa nova matriz e um novo valor médio é calculado. O ciclo se repete até que todos os valores sejam agrupados.
Exemplo de trabalho:
Pegue um conjunto de dados extremamente simplificado com várias espécies de baleias e golfinhos. Sou biólogo e posso garantir que muito mais propriedades são usadas para construir
árvores filogenéticas . Mas, no nosso exemplo, nos restringimos ao comprimento característico do corpo de seis espécies de mamíferos marinhos. Haverá duas etapas de cálculos.
Etapa 1 : a matriz de distâncias entre todas as vistas é calculada. Usaremos a métrica euclidiana que descreve a distância entre nossos dados, como os assentamentos no mapa. Você pode obter a diferença no comprimento dos corpos de cada par lendo o valor na interseção da coluna e linha correspondentes.
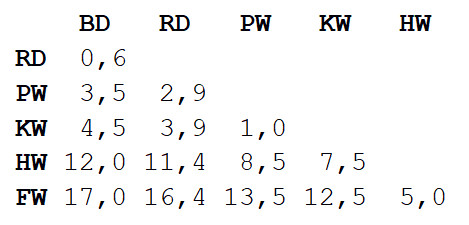Etapa 2 : pegue um par de duas espécies mais próximas umas das outras. Nesse caso, é um golfinho-nariz-de-garrafa e um golfinho-cinzento, no qual o comprimento médio do corpo é de 3,3 m.
Repetimos o passo 1, calculando novamente a matriz de distância, mas desta vez combinamos golfinho-nariz-de-garrafa e golfinho-cinzento em um objeto com um comprimento de corpo de 3,3 m.
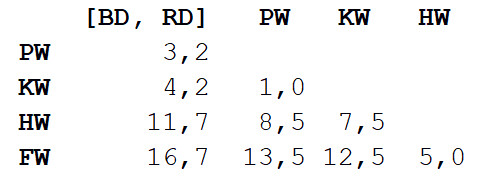
Agora repetimos o passo 2, mas com uma nova matriz de distância. Desta vez, a moagem e a baleia assassina serão as mais próximas, então vamos colocá-las em casal e calcular a média - 7 m.
Em seguida, repita o passo 1: calcule novamente a matriz de distâncias, mas com a baleia moída e a baleia assassina na forma de um único objeto com 7 m de comprimento.
Repita a etapa 2 com esta matriz. A menor distância (3,7 m) será entre os dois objetos combinados, portanto, nós os combinaremos em um objeto ainda maior e calcularemos o valor médio - 5,2 m.
Em seguida, repita a etapa 1 e calcule uma nova matriz combinando golfinho-nariz-de-garrafa / golfinho cinza com moagem / baleia assassina.
Repita a etapa 2. A menor distância (5 m) será entre a jubarte e a barbatana, por isso combinamos e calculamos a média - 17,5 m.
Novamente, o passo 1: calcule a matriz.
Por fim, repita o passo 2 - resta apenas uma distância (12,3 m), portanto, uniremos todos em um objeto e pararemos. Aqui está o que aconteceu:
[[[BD, RD],[PW, KW]],[HW, FW]]
O objeto possui uma estrutura hierárquica (lembre-se de
JSON ), para que possa ser exibido como um gráfico em árvore ou dendrograma. O resultado é semelhante a uma árvore genealógica. Quanto mais próximos dois valores estiverem de uma árvore, mais semelhantes ou mais estreitamente conectados.
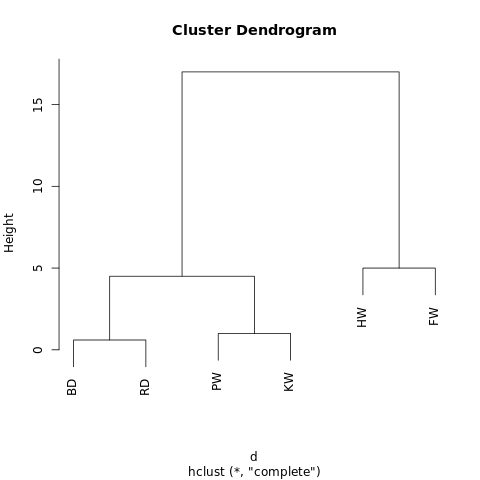Um dendograma simples gerado usando o R-Fiddle.orgA estrutura do dendrograma permite entender a estrutura do próprio conjunto de dados. Em nosso exemplo, temos dois galhos principais - um com jubarte e barbatana, o outro com um golfinho-nariz-de-garrafa / golfinho-cinzento e uma baleia grind / killer.
Na biologia evolutiva, conjuntos de dados muito maiores, com muitas espécies e uma abundância de caracteres, são usados para identificar relações taxonômicas. Fora da biologia, o cluster hierárquico é aplicado nas áreas de mineração de dados e aprendizado de máquina.
Essa abordagem não requer previsão do número necessário de clusters. Você pode dividir o dendrograma resultante em grupos, “aparando” a árvore na altura desejada. Você pode escolher a altura de diferentes maneiras, dependendo da resolução desejada do cluster de dados.
Por exemplo, se o dendrograma acima for cortado a uma altura de 10, cruzaremos os dois ramos principais, dividindo o dendrograma em duas colunas. Se cortar a uma altura de 2, divida o dendrograma em três grupos.
Outros algoritmos de cluster hierárquico podem diferir em três aspectos daqueles descritos neste artigo.
A coisa mais importante é a abordagem. Aqui usamos o método
aglomerativo : começamos com valores individuais e os agrupamos ciclicamente até obter um grande agrupamento. Uma abordagem alternativa (e computacionalmente mais complexa) implica a sequência inversa: primeiro um grande cluster é criado e, em seguida, é dividido sequencialmente em clusters cada vez menores até que valores separados permaneçam.
Existem também vários métodos para calcular matrizes de distância. As métricas euclidianas são suficientes para a maioria das tarefas, mas
outras métricas são mais adequadas em algumas situações.
Finalmente, o critério de ligação pode variar. O relacionamento entre os clusters depende da proximidade entre eles, mas a definição de "proximidade" pode ser diferente. Em nosso exemplo, medimos a distância entre os valores médios (ou "centróides") de cada grupo e combinamos os grupos mais próximos em pares. Mas você pode usar outra definição.
Suponha que cada cluster consiste em vários valores discretos. A distância entre dois clusters pode ser definida como a distância mínima (ou máxima) entre qualquer um de seus valores, conforme mostrado abaixo. Para diferentes contextos, é conveniente usar diferentes definições do critério de junção.
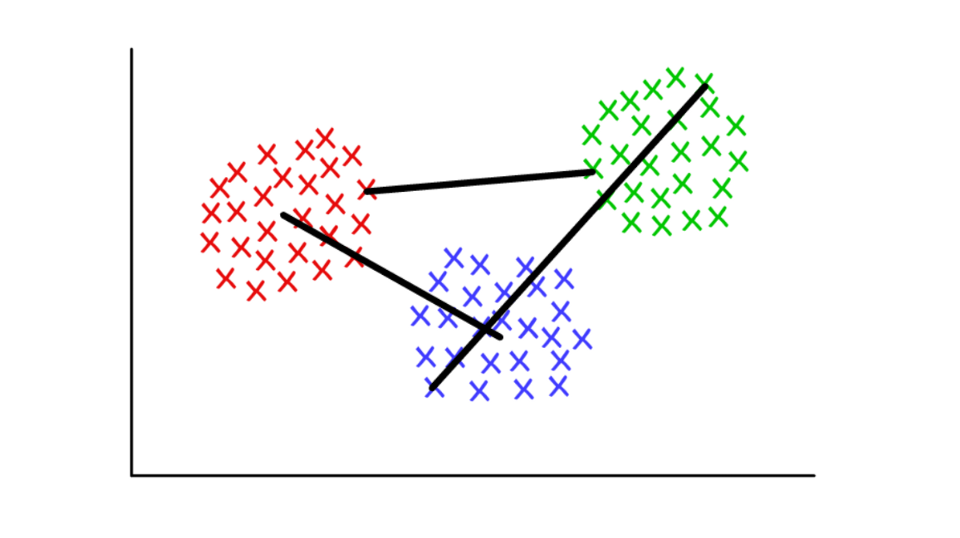Vermelho / azul: piscina centróide; vermelho / verde: combinação baseada em mínimos; verde / azul: mesclando com base em altas.Definição de comunidades em gráficos (detecção de comunidade de gráficos)
Usado por:
Quando seus dados podem ser apresentados na forma de uma rede, ou "gráfico".
Como funciona:
Uma comunidade em um gráfico pode ser definida aproximadamente como um subconjunto de vértices que estão mais conectados entre si do que com o restante da rede. Existem diferentes algoritmos de definição de comunidade baseados em definições mais específicas, como Edge Betweenness, Modularity-Maximsation, Walktrap, Percolation de Clique, Leading Eigenvector ...
Exemplo de trabalho:
A teoria dos grafos é um ramo da matemática muito interessante que nos permite modelar sistemas complexos na forma de conjuntos abstratos de “pontos” (vértices, nós) conectados por “linhas” (arestas).
Talvez a primeira aplicação de gráficos que vem à mente seja o estudo de redes sociais. Nesse caso, os picos representam pessoas conectadas por costelas a amigos / assinantes. Mas você pode imaginar qualquer sistema na forma de uma rede se puder justificar o método de conexão significativa dos componentes. Aplicações inovadoras de agrupamento usando a teoria dos grafos incluem a extração de propriedades de dados visuais e a análise de redes reguladoras genéticas.
Como um exemplo simples, vejamos o gráfico abaixo. Isso mostra os oito sites que eu visito com mais frequência. Os links entre eles são baseados em links nos artigos da Wikipedia. Esses dados podem ser coletados manualmente, mas para projetos grandes, é muito mais rápido escrever um script Python. Por exemplo, este:
https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .
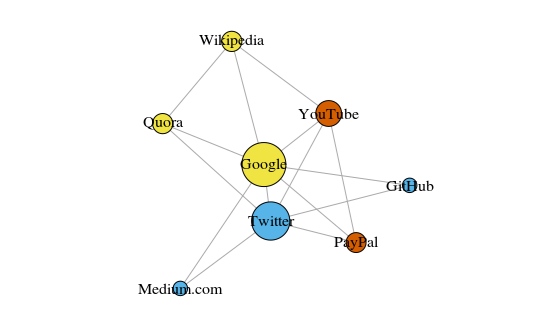O gráfico é construído usando o pacote igraph para R 3.3.3A cor dos picos depende da participação nas comunidades e o tamanho depende da centralidade. Observe que os mais centrais são o Google e o Twitter.
Além disso, os clusters resultantes refletem com muita precisão tarefas reais (esse é sempre um indicador importante de desempenho). Os vértices que representam os sites de link / pesquisa são destacados em amarelo; sites destacados em azul para publicações on-line (artigos, tweets ou código); destacados em vermelho estão o PayPal e o YouTube, fundados por ex-funcionários do PayPal. Boa dedução para o computador!
Além de visualizar grandes sistemas, o verdadeiro poder das redes reside na análise matemática. Vamos começar convertendo a imagem da rede em um formato matemático. A seguir,
é apresentada a matriz de
adjacência da rede.
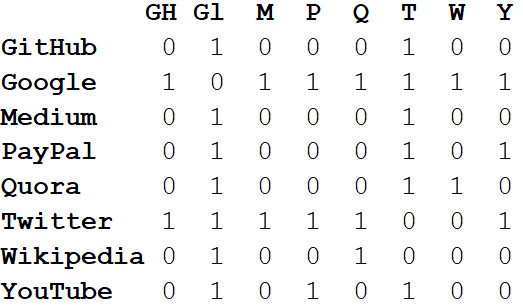
Os valores nas interseções de colunas e linhas indicam se há uma aresta entre esse par de vértices. Por exemplo, entre Médio e Twitter, é, portanto, na interseção dessa linha e coluna, que está 1. E entre Médio e PayPal, não há aresta; portanto, na célula correspondente, há 0.
Se representarmos todas as propriedades da rede na forma de uma matriz de adjacência, isso nos permitirá tirar todos os tipos de conclusões úteis. Por exemplo, a soma dos valores em qualquer coluna ou linha caracteriza o
grau de cada vértice - ou seja, o número de objetos conectados a esse vértice. Geralmente indicado pela letra
k .
Se somarmos os graus de todos os vértices e dividirmos por dois, obtemos L - o número de arestas na rede. E o número de linhas e colunas é igual a N - o número de vértices na rede.
Conhecendo apenas k, L, N e os valores em todas as células da matriz de adjacência A, podemos calcular a modularidade de qualquer cluster.
Suponha que agrupamos uma rede em várias comunidades. Em seguida, você pode usar o valor da modularidade para prever a "qualidade" do cluster. Uma modularidade mais alta indica que dividimos a rede em comunidades "exatas", e uma modularidade mais baixa sugere que os clusters são formados mais por acaso do que razoavelmente. Para tornar mais claro:
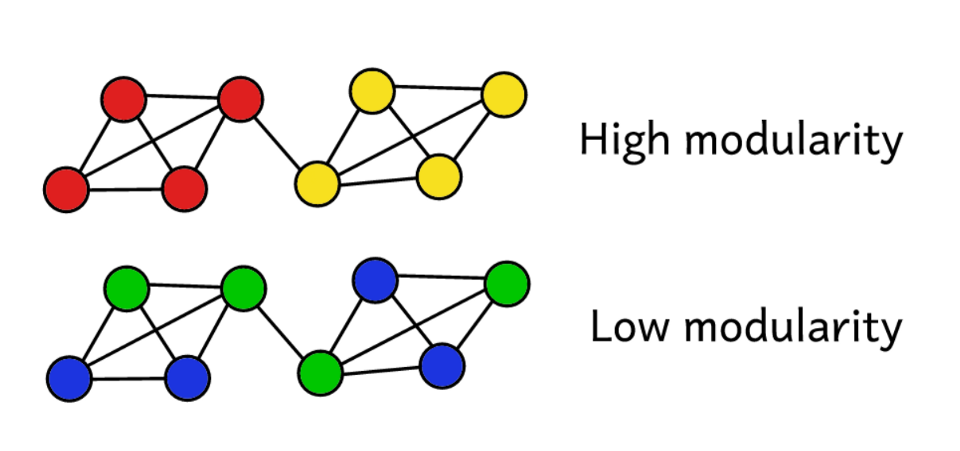
A modularidade é uma medida da "qualidade" dos grupos.
A modularidade pode ser calculada usando a seguinte fórmula:
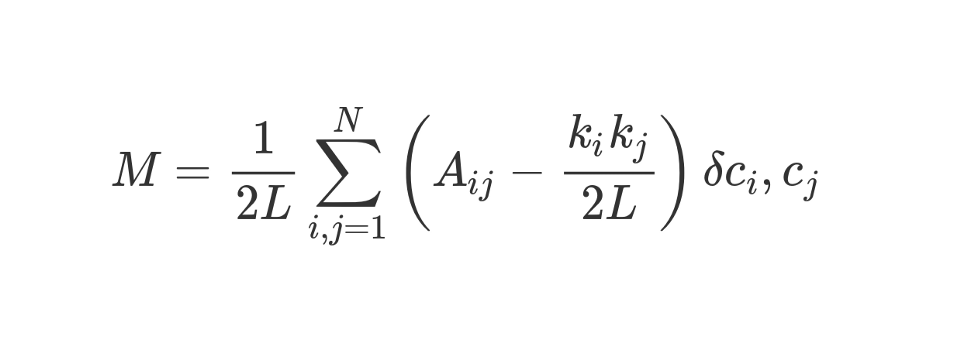
Vamos olhar para esta fórmula bastante impressionante.
M , como você sabe, isso é modularidade.
O coeficiente
1 / 2L significa que dividimos o restante do "corpo" da fórmula por 2L, ou seja, pelo número duplo de arestas na rede. Em Python, pode-se escrever:
sum = 0 for i in range(1,N): for j in range(1,N): ans =
O que é
#stuff with i and j ? O bit entre parênteses nos diz para subtrair (k_i k_j) / 2L de A_ij, onde A_ij é o valor na matriz na interseção da linha ie coluna j.
Os valores k_i e k_j são os graus de cada vértice. Eles podem ser encontrados somando os valores na linha ie coluna j, respectivamente. Se os multiplicarmos e dividirmos por 2L, obteremos o número esperado de arestas entre os vértices iej se a rede for misturada aleatoriamente.
O conteúdo dos colchetes reflete a diferença entre a estrutura real da rede e a esperada se a rede foi reconstruída aleatoriamente. Se você brinca com os valores, a modularidade mais alta será A_ij = 1 e baixa (k_i k_j) / 2L. Ou seja, a modularidade aumenta se houver uma aresta "inesperada" entre os vértices iej.
Finalmente, multiplicamos o conteúdo dos colchetes pelo que é indicado na fórmula como δc_i, c_j. Esta é a função Kronecker-delta. Aqui está sua implementação em Python:
def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A")
Sim, tão simples. A função recebe dois argumentos e, se forem idênticos, retornará 1 e, se não, então 0.
Em outras palavras, se os vértices iej caírem em um cluster, então δc_i, c_j = 1. E se eles estiverem em clusters diferentes, a função retornará 0.
Como multiplicamos o conteúdo dos colchetes pelo símbolo Kronecker, o resultado da soma investida the será mais alto quando os vértices dentro de um cluster forem conectados por um grande número de arestas "inesperadas". Assim, a modularidade é um indicador de quão bem um gráfico é agrupado em comunidades individuais.
A divisão por 2L limita a modularidade superior à unidade. Se a modularidade for próxima de 0 ou negativa, isso significa que o cluster atual da rede não faz sentido. Ao aumentar a modularidade, podemos encontrar uma maneira melhor de agrupar a rede.
Observe que, para avaliar a "qualidade" do agrupamento de um gráfico, precisamos determinar com antecedência como ele será agrupado. Infelizmente, a menos que a amostra seja muito pequena, devido à complexidade computacional, é simplesmente fisicamente impossível passar estupidamente por todos os métodos de agrupar um gráfico comparando sua modularidade.
A Combinatorics sugere que, para uma rede com 8 vértices, existem 4.140 métodos de agrupamento. Para uma rede com 16 vértices, já haverá mais de 10 bilhões de maneiras, para uma rede com 32 vértices, 128 septilhões e para uma rede com 80 vértices, o número de métodos de agrupamento excederá o
número de átomos no Universo observável .
Portanto, em vez de enumeração, usaremos o método heurístico, que ajudará a calcular relativamente facilmente clusters com o máximo de modularidade. Esse é um algoritmo chamado
Fast-Greedy Modularity-Maximization , um tipo de análogo ao algoritmo de agrupamento hierárquico aglomerado descrito acima. Em vez de combinar com base na proximidade, o Mod-Max une comunidades, dependendo das mudanças na modularidade. Como funciona:
Primeiro, cada vértice é atribuído à sua própria comunidade e a modularidade de toda a rede é calculada - M.
Etapa 1 : para cada par de comunidades conectadas por pelo menos uma borda, o algoritmo calcula a alteração resultante na modularidade ΔM no caso de combinar esses pares de comunidades.
Etapa 2 : então um par é obtido, quando combinado, ΔM será máximo e combinado. Para esse cluster, uma nova modularidade é calculada e armazenada.
As etapas 1 e 2 são
repetidas : cada vez que um par de comunidades se junta, o que dá o maior AM, um novo esquema de agrupamento e seu M.
As iterações
param quando todos os vértices são agrupados em um cluster enorme. Agora, o algoritmo verifica os registros armazenados e encontra o esquema de cluster com a mais alta modularidade. É ela quem volta como uma estrutura comunitária.
Era computacionalmente difícil, pelo menos para as pessoas. A teoria dos grafos é uma fonte rica de problemas computacionais difíceis e de NP-hard. Usando gráficos, podemos tirar muitas conclusões úteis sobre sistemas e conjuntos de dados complexos. Pergunte a Larry Page, cujo algoritmo PageRank - que ajudou o Google a se transformar de uma startup para uma dominante global em menos de uma geração - é inteiramente baseado na teoria dos grafos.
Hoje, estudos sobre a teoria dos grafos se concentram na identificação de comunidades. Existem muitas alternativas para o algoritmo Modularity-Maximization, que, embora útil, não deixa de ter suas desvantagens.
Primeiro, com uma abordagem aglomerativa, comunidades pequenas e bem definidas são frequentemente combinadas em comunidades maiores. Isso é chamado de limite de resolução - o algoritmo não aloca comunidades menores que um determinado tamanho. Outra desvantagem é que, em vez de um pico global pronunciado e facilmente alcançável, o algoritmo Mod-Max procura gerar um amplo "platô" a partir de muitos valores próximos de modularidade. Como resultado, é difícil destacar o vencedor.
Outros algoritmos usam métodos diferentes para definir comunidades. Por exemplo, Edge-Betweenness é um algoritmo de divisão (divisão) que começa agrupando todos os vértices em um cluster enorme. Em seguida, as arestas menos "importantes" são removidas iterativamente até que todos os vértices sejam isolados. O resultado é uma estrutura hierárquica na qual os vértices estão mais próximos, mais semelhantes.
O algoritmo, Clique Percolation, leva em consideração possíveis interseções entre comunidades. Há um grupo de algoritmos baseados em
caminhada aleatória em um gráfico e existem métodos de
agrupamento espectral que lidam com a decomposição espectral (composição automática) da matriz de adjacência e outras matrizes dela derivadas. Todas essas idéias são usadas para destacar recursos, por exemplo, na visão de máquina.
Não analisaremos exemplos de trabalho para cada algoritmo em detalhes. , , 20 .
Conclusão
, - , , . , , 20-40 .
, — , . , , .
, , , , . , - , , ? - !