Um artigo sobre a análise do jogo por uma rede comercial conhecida despertou
grande interesse no
Cloud4Y . Aqui estão algumas passagens para você se atualizar:
Certa vez, em uma ensolarada manhã de primavera, lendo um fórum da cidade, deparei-me com um link com um jogo simples de uma rede comercial conhecida. O jogo (ação) dedicado à Copa do Mundo foi um campo simples, três a três, cheio de bolas de futebol. Ao clicar na bola, abrimos uma imagem com um produto específico. Ao abrir três fotos idênticas, foi garantido ao participante o recebimento gratuito deste produto em uma das lojas da rede. Além disso, sob uma das bolas havia uma imagem de um cartão vermelho, cuja abertura significou o fim do jogo.
O autor do artigo começou a investigar os motivos de sua perda e, com base nos resultados dos cálculos, descobriu o seguinte:
Um rápido esboço das fórmulas em um guardanapo, e a probabilidade de ganhar é de 1/4. Em 5 campos, tive que mexer, mas a probabilidade calculada também foi de 25%.
...
Ao executar o script, obtive um resultado inesperado - 25% dos ganhos. Tendo jogado com o número de elementos vencedores e o número total de campos, descobri que a probabilidade de ganhar em um jogo desse tipo não depende do número de campos e é igual a um dividido pelo número de elementos vencedores aumentado em um.
Estávamos interessados na correção desse cálculo e, substituindo o guardanapo pelo Excel, começamos a trabalhar em busca da verdade matemática. Os leitores que gostam da teoria das probabilidades são convidados a usar o gato, a fim de verificar a correção de nossos cálculos.
Primeiro de tudo, descobrimos as regras do jogo. Nisso, sem saber, o usuário de Habr
Stecenko ajudou em seu
comentário . Ele também escreve:
Se você olhar para o script do autor, está escrito no pressuposto de que DEVE haver três cartas de um produto no campo, uma carta de cinco outros produtos e uma carta vermelha, enquanto a descrição do jogo não segue absolutamente isso - as regras não dizem que a combinação vencedora deve estar presente em campo.
As regras, no entanto, dizem que um total de 26 produtos está envolvido. Acontece que a emissão de 9 cartões é gerada: 8 cartões são combinações de 26 produtos com repetições e um cartão é vermelho.
Sob tais condições, o cálculo da probabilidade matemática de ganhar é um pouco mais complicado do que o autor do post original sugeriu. O jogo consiste em várias camadas:- A probabilidade de abrir N cards sem abrir o vermelho é a probabilidade de uma duração diferente do jogo, independentemente de haver um prêmio.
- A probabilidade de coletar uma combinação de 3 cartas com as mesmas mercadorias. Essa probabilidade varia de acordo com a duração do jogo. É importante entender que um conjunto de 8 cartas com mercadorias e sempre uma vermelha não necessariamente contém pelo menos um par de cartas idênticas, sem mencionar três de uma vez.
Vamos começar com um simples - entender como o número de participantes diminuirá com o aumento do número de cartões que eles abrem devido à regra do cartão vermelho.
Probabilidades de diferentes comprimentos de jogo
Calculamos como é provável que, para N testes (cartões abertos), o vermelho seja aberto.UPD: Inicialmente, calculamos a probabilidade de abertura em vermelho usando uma distribuição binomial. Isso não nos garantiu estritamente 1 cartão vermelho, com essa distribuição provavelmente havia um cartão vermelho, mas poderia haver 0 ou todos os 9 com uma probabilidade muito, muito pequena. Mais uma vez, obrigado a Stecenko por apontar um erro no comentário e sugerir a solução certa .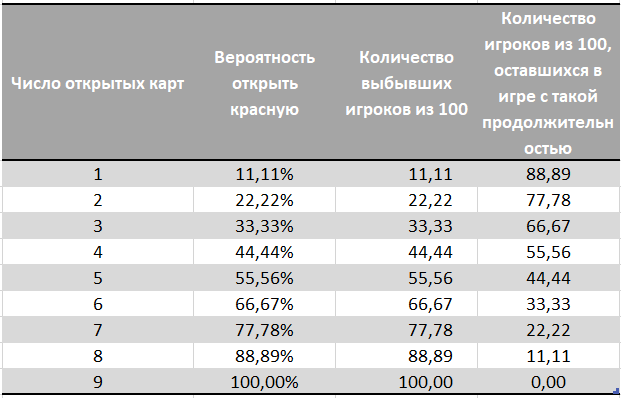
A última coluna mostra quantos jogadores em cada cem permanecem no jogo com essa duração. O restante dos jogadores é eliminado devido ao cartão vermelho, sem saber se houve uma combinação vencedora no conjunto de cartões emitido.
Agora calcularemos as probabilidades de coletar uma combinação de três cartões com as mesmas mercadorias. Esta é uma condição para receber um prêmio.
Chances de prêmios
Nós decompomos o jogo logicamente. Abrimos a primeira carta e, em seguida, selecionamos o par para esta carta, selecionamos as três para o par. Com essa abordagem, podemos calcular a probabilidade de obter três cartas idênticas em três ou mais tentativas, com base no fato de que existem 26 produtos no jogo.
Para tarefas com um número fixo de testes ou testes, se o resultado de qualquer teste puder ser apenas sucesso ou falha, os testes são independentes e a probabilidade de sucesso permanece constante ao longo do experimento, usaremos a fórmula de Bernoulli - no Excel, a função BINOM.DIS.
Usando a função BINOM.RASP, você pode calcular, por exemplo, a probabilidade de que dois dos próximos três recém-nascidos sejam meninos. Qual é a probabilidade de descobrir três iguais em três tentativas?
= BINOM.RASP (3; 3; 1/26; 0) por máscara
= BINOM.DISP (número de sucessos; número de tentativas; probabilidade de sucesso; integral)
Ou aqui está a fórmula para calcular a probabilidade de obter 3
mercadorias idênticas e certas em 8 tentativas.
= BINOM.RASP (3; 8; 1/26; 0), certo?
Na verdade não. Quando atingimos a duração do jogo em 4 tentativas, não permitindo a abertura do vermelho e continuando a jogar, temos uma situação com a possibilidade de dois pares selecionarem três vencedores.
Convencionalmente, duas mercadorias de 26 são A e B. Nossos cartões abertos são A-B-A-B. A probabilidade não é mais 1/26, mas 1/26
+ (1/26) * "A probabilidade de dois pares por uma determinada duração do jogo .
"A probabilidade de dois pares para uma determinada duração do jogo = BINOM.DISP (2; 5; 1/26; 0) ^ 2
Ao chegarmos a um jogo mais longo na 7ª tentativa, obtemos combinações como A-B-A-B-B-B. Isso significa que a probabilidade agora é igual
= 1/26 * (1 + BINOM.RASP (2; 7; 1/26; 0) ^ 2 + BINOM.RASP (2; 7; 1/26; 0) ^ 3) e estamos procurando um terceiro cartão para 1, 2 ou três pares.
UPD: Além disso, inicialmente não levamos em conta que a primeira tentativa em nosso cálculo dos ganhos, livre da probabilidade de escolher o vermelho, é a descoberta de qualquer um dos 26 produtos, o que significa 100% de sucesso. O número de repetições de um produto na matriz é o número de correspondências com qualquer produto, o que significa que duas repetições em um único produto são suficientes para vencer e não coincidem com um resultado previsto específico. Assim, a primeira escolha de qualquer carta e duas tentativas de pegar mais duas da mesma formam um total de três experimentos.Conhecendo as probabilidades, estamos construindo uma matriz:
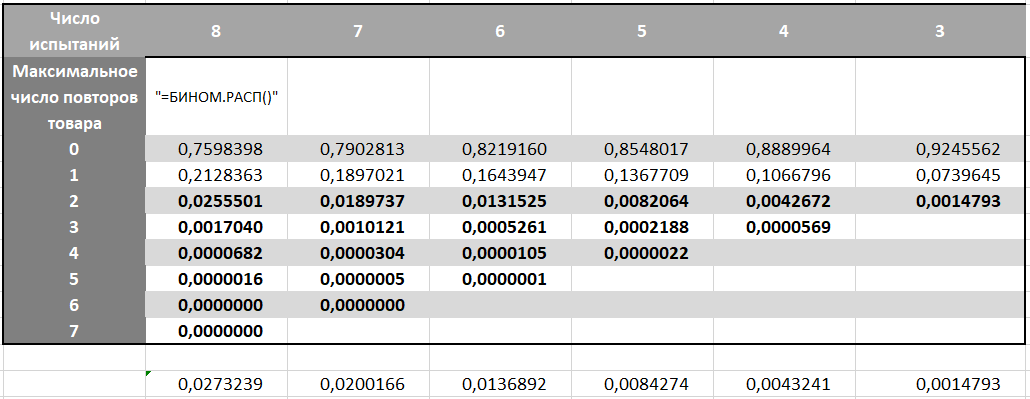
Nele encontramos a probabilidade de cada número máximo de repetições de um produto para cada variante da duração do jogo. Lembre-se de que a probabilidade de ganhar muda na quarta tentativa e no 7, o que significa que levamos isso em consideração na fórmula BINOM.RASP
Precisamos de opções com um número máximo de repetições de qualquer produto de 3 ou mais. Como o jogo irá parar assim que coletarmos os três, adicionamos as probabilidades por colunas na área em negrito.
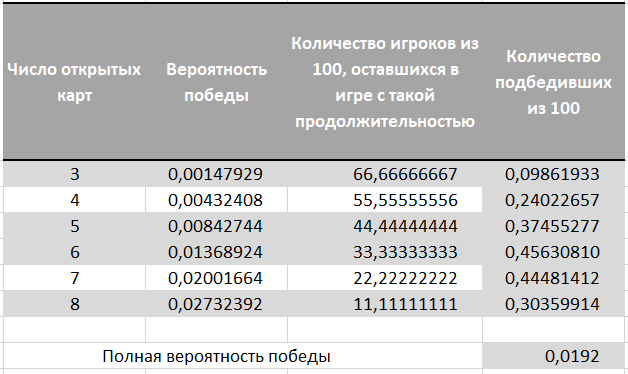
Em seguida, multiplicamos as chances da duração de cada jogo pelas chances de ganhar um prêmio com essa duração. Resumindo, temos uma probabilidade de 0,0192 ou 192 vencedores por 10.000 jogadores.
Sim, na verdade é uma probabilidade muito baixa. Nem um pouco de 25%. Vejamos as regras do jogo novamente:
8. Fundo de premiação:
8.1 Prêmios disponíveis: nomes e quantidades
...
Total 166.000
Dividimos 116.000 pela probabilidade de ganhar e recebemos cerca de 6 milhões de participantes para disputar todos os prêmios. Lembre-se de que em 1º de janeiro de 2018, de acordo com Rosstat, havia 146 938 921 residentes permanentes na Rússia. Aparentemente, essa é a idéia dos organizadores do jogo - dar a chance de ganhar quase todos os cidadãos da Rússia.UPD: A probabilidade final mudou após as alterações. Agora podemos testar nossos cálculos na prática com a ajuda de scripts, mas a dádiva de Deus aos matemáticos e teóricos das gerações anteriores é incrível, que calculou um número tão grande de probabilidades, encontrando a solução certa no papel e usando experimentos mentais.A análise do código mostrou ao autor da publicação original que, mesmo antes do início do jogo, o script “conhece” seu resultado, mas ninguém sabe qual resultado predeterminado o script dará a um usuário específico. Conhecendo o lado matemático da questão, você poderá fazer sua própria conclusão sobre a honestidade dos organizadores.