Lógica difusa para controlar
O texto é baseado em materiais do livro de V. Gostev. "Reguladores nebulosos em sistemas de modelagem automática". Como todas as publicações sérias sobre o assunto, este livro está sobrecarregado com cálculos matemáticos e difícil para o leitor despreparado. Enquanto isso, os princípios de criação e uso da lógica difusa são bastante simples e claros. Este texto é uma tentativa de traduzir um exemplo de um livro de uma linguagem matemática para uma de engenharia.
Uma sequência possível de projetar um controlador baseado em lógica nebulosa é mostrada complicando sequencialmente regras lógicas e selecionando parâmetros usando métodos de otimização.
Declaração do problema
Considere a síntese de um controlador PID digital e um controlador nebuloso para um sistema de controle de mísseis por ângulo de ataque. Usando modelagem matemática, determinamos os processos no sistema e fazemos uma avaliação comparativa da qualidade do sistema usando controladores sintetizados.
Tomando o ângulo de ataque como coordenada de saída do míssil:  e para a entrada coordenar o ângulo de direção
e para a entrada coordenar o ângulo de direção  defina a função de transferência do foguete na forma:
defina a função de transferência do foguete na forma:
 onde:
onde:
 - coeficiente de conversão de foguetes,
- coeficiente de conversão de foguetes,
 - coeficiente de amortecimento,
- coeficiente de amortecimento,
 - constante de tempo.
- constante de tempo.
A seguir, a "função de transferência" não é usada em uma definição clássica estrita, como a razão das transformações de Laplace.
No estudo do sistema de controle, suponha que a dependência dos parâmetros do foguete no tempo de voo seja determinada da seguinte forma:

Para simplificar os cálculos, descrevemos o mecanismo de direção pela função de transferência do link de integração  Nesse caso, a entrada do sistema
Nesse caso, a entrada do sistema  - dado ângulo de ataque, saída do sistema
- dado ângulo de ataque, saída do sistema  O ângulo de ataque é calculado pelo foguete, m (t) é o sinal de controle na saída do controlador e o objeto de controle é descrito pela função geral de transferência:
O ângulo de ataque é calculado pelo foguete, m (t) é o sinal de controle na saída do controlador e o objeto de controle é descrito pela função geral de transferência:

(O equipamento de direção analógico e o foguete estão incluídos no objeto de controle).
A lei da variação da ação de entrada é dada pelo polinômio:

É necessário desenvolver um controlador que garanta o desenvolvimento do efeito de entrada usando um controlador PID e um controlador baseado na lógica difusa.
Selecionar os coeficientes dos reguladores.
Compare o transitório com o controlador PID e o controlador com base na lógica difusa.
Modelo de objeto dinâmico
Crie um modelo dinâmico em um ambiente de modelagem estrutural.
O circuito do modelo em si é mostrado na Figura 1.
A ação especificada é configurada na forma de um bloco constante; uma variável do script é configurada como parâmetros. Os parâmetros da função de transição são definidos na forma de variáveis.
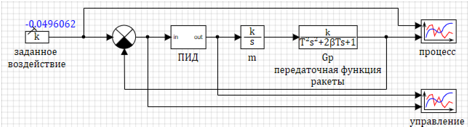 Figura 1. Diagrama de um modelo dinâmico de um foguete.
Figura 1. Diagrama de um modelo dinâmico de um foguete.Configuração do regulador
O bloco PID é um submodelo (Fig. 2), que usa o bloco padrão “Discrete PID controller”. A taxa de amostragem é selecionada igual a 0,001 seg.
 Figura 2. Controlador PID com circuito de sintonia.
Figura 2. Controlador PID com circuito de sintonia.Os parâmetros do controlador são definidos na forma de nomes de sinais globais do projeto
Kp, Ki, Kd. Isso permite alterar os parâmetros durante a simulação e ajustar o regulador.
O bloco
“Otimização” foi utilizado para ajustar o regulador, o critério de otimização é o desvio padrão mínimo.
A unidade de otimização realiza otimização durante todo o processo de transição. O resultado da otimização é um vetor de três coeficientes, que é enviado ao bloco "Gravar na lista de sinais", onde os valores calculados são transferidos para os sinais e, consequentemente, os valores dos coeficientes do PID mudam. Para configurar o controlador, definimos os seguintes parâmetros de otimização:
Valores iniciais de todos os coeficientes
1.O intervalo de seleção é definido de
-50 a
+50Precisão de seleção
0,001Desvio padrão máximo após otimização
0,01Nesse caso, a unidade de otimização calculou os seguintes valores ótimos dos coeficientes:
Kp = -1,7498597; Ki = 17,891995; Kd = 11,606602 .
Com esses coeficientes, o desvio padrão no transiente especificado foi de
0,008738090
Figura 3. Transitório.
| 
Figura 4. Gerenciamento. |
Controlador lógico difuso
As principais vantagens de um controlador baseado em lógica difusa são a simplicidade e clareza da formação das regras para controlar o objeto.
Por exemplo, no livro "Reguladores nebulosos em sistemas de modelagem automática", as regras de regulação nebulosas para controlar o foguete pelo ângulo de ataque são descritas na forma de uma expressão matemática:

onde

- erro de sistema, erros de alteração de velocidade (primeira derivada), erros de aceleração (segunda derivada);
m - controle a ação no objeto;

- estimativas linguísticas de erro, taxa de variação de erro (primeira derivada) de erro e segunda derivada de erro, consideradas conjuntos difusos definidos em um conjunto universal

;

- estimativas lingüísticas da ação de controle do objeto, selecionadas a partir dos conjuntos de termos da variável
mO leitor pode perguntar: como está sua mãe, desculpe, entendeu?
Às vezes, surgem dúvidas em mim de que os próprios matemáticos entendam o que escreveram. Por trás das voltas matemáticas abstrusas, o grande segredo das regras da regulação nebulosa está oculto. Aqui está:
reduzir muito
norma - não toque
pequeno - aumentoSe você traduzir da língua matemática do pássaro para o russo, a expressão

literalmente significa o seguinte:
Se é
mais do que o normal e o
desvio aumenta e
a taxa de crescimento aumenta ,
diminuímos .
Se a
norma não muda e a
velocidade é constante , então
não mudamos .
Se estiver
abaixo do normal e
cair e
a taxa de queda aumentar ,
aumente .
Se você entende o que realmente está oculto por trás do nevoeiro matemático, pode abordar a criação de reguladores de maneira mais consciente e obter resultados mais interessantes.
Pouco de teoria
Para resolver o problema de ajustar o ângulo de ataque, precisamos obter três termos do valor do desvio contínuo - menos, norma, mais. O mesmo deve ser feito para a primeira derivada do desvio e a segunda derivada do desvio. Este é o primeiro estágio da inferência difusa - faseamento.
Para obter os termos, precisamos definir o valor numérico do parâmetro para cada termo. Por exemplo: "Pouco" = -1; "Norma" = 0; “Many” = 1. Para a fase, usaremos funções triangulares. As funções crescem à medida que você se aproxima do valor definido e diminuem à medida que você se afasta. Duas opções para funções triangulares são mostradas na Figura 5:

 Figura 5. Funções de associação triangular.
Figura 5. Funções de associação triangular.Conhecendo o desvio (x1), podemos encontrar os valores da função de associação para os termos mais (linha vermelha), norma (linha verde), menos (linha azul). Os valores variam de 0 a 1.
Observe que no gráfico esquerdo as funções extremas não são muito "triangulares". Se considerarmos isso do ponto de vista da matemática abstrata, as funções no gráfico à direita são mais "bonitas". Mas, se você se lembra do "principal segredo das regras da inferência difusa", o gráfico da esquerda está mais correto. De fato:
Considere a regra
"Adicionar - pequeno" , se tivermos um valor de -1, então
"pequeno" = 1 (linha vermelha) é verdadeiro para os dois gráficos. E se tivermos um valor de -2? Logicamente, também devemos
adicionar . No gráfico esquerdo, em -2, é:
“little = 1” , mas no gráfico direito, temos
“little” = 0, o que obviamente não é verdade. O mesmo vale para a regra
"reduzir muito" .
Fases de funções triangulares “honestas” podem levar ao fato de que, quando o valor ultrapassa o intervalo de definição de funções, obtemos 0 para todos os termos, o que, por sua vez, pode levar à ausência de impacto no objeto.
O problema inverso é a despaseificação. Para calcular o impacto, você precisa executar a transformação inversa - temos os valores das funções de associação para reduzir, não alterar, aumentar o intervalo (
0 ... 1 ) (funções triangulares) e o intervalo de efeitos que podemos ter, e devemos obter um dos três número é um impacto específico.
Você pode obter o impacto de várias maneiras, por exemplo, no centro de massa da figura. A Figura 6 mostra o estado do controlador, em que os valores dos termos diminuem
0,3 não alteram
0,6 e aumentam
0,8 com uma faixa de impacto regulatório
-30..30 impacto resultante =
4.1.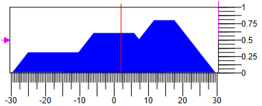 Figura 6. Desfazificação da ação de controle
Figura 6. Desfazificação da ação de controleOutra opção para a desfazificação está no centro de massa dos pontos. A Figura 7 mostra uma opção em que, para os mesmos valores dos termos e da faixa de controle, obtemos outra resposta
8.82 :
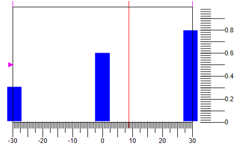 Figura 7. Desfazificação pelo centro de massa de pontos.
Figura 7. Desfazificação pelo centro de massa de pontos.Deve-se entender que, além do método de inferência, a forma da função de associação também afeta o resultado. Por exemplo, você pode escolher essas funções triangulares para as quais a base do triângulo é a mesma, apenas os vértices diferem. (veja a fig. 8).
 Figura 8. Funções de associação triangular com uma base.
Figura 8. Funções de associação triangular com uma base.Nesse caso, para reduzir o resultado da fase com os mesmos valores dos termos 0,3, não altere 0,6 e aumente -0,8 com a faixa de impacto regulatório -30, 30 impacto resultante =
5,27 .
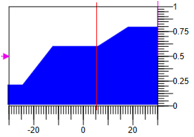 Figura 9. Desfazificação por cálculo de área.
Figura 9. Desfazificação por cálculo de área.Armado com o conhecimento secreto da lógica fuzzy, criaremos um modelo de controlador. Deixamos o modelo de foguete igual ao do controlador PID (veja a Fig. 1), mas no submodelo do controlador montamos o circuito mostrado na Figura 10.
 Figura 10. O circuito do controlador baseado na lógica difusa.
Figura 10. O circuito do controlador baseado na lógica difusa.Na entrada do regulador, é aplicada uma incompatibilidade entre o ângulo de ataque especificado e o real (medido). Após a entrada, existe um bloco "Extrapolador", que fornece a conversão de um sinal contínuo em um sinal discreto com um determinado período de amostragem (0,001 s é o mesmo que o de um controlador PID discreto).
Depois disso, o primeiro e o segundo desvio derivado são calculados. Para isso, calculamos a diferença entre o valor atual e o valor com um atraso para o período de quantização, dividindo-o pelo tempo de atraso (coeficiente no bloco de comparação). Assim, obtemos três entradas: erro do sistema, taxa de variação (primeira derivada) do erro, aceleração (segunda derivada) do erro.
O valor das variáveis de entrada é convertido por blocos de fase em funções triangulares. Para cada variável, obtemos três variáveis linguísticas (nove no total).
Os blocos do desmultiplexador geram vetores em variáveis linguísticas para formar regras. No diagrama, os nomes das variáveis são assinados na ordem em que estão nos vetores.
O desvio no nosso caso é a diferença entre o conjunto e o medido. Se um valor negativo significa que o ângulo de ataque é maior que o conjunto, devemos reduzi-lo. E, portanto, pelo contrário, se o desvio for positivo, o ângulo medido é menor que o especificado, devemos aumentá-lo.
(Mais - reduza, menos - aumente, a norma - não toque) .
O resultado também possui três variáveis linguísticas “reduzir”, “não mudar”, “aumentar”. O multiplexador coleta os valores em um vetor e os envia para o bloco de saída difusa. Agora que temos todas as variáveis, podemos escrever as regras de inferência fuzzy na forma de um diagrama.
- Se mais do que o normal, o desvio aumenta e a taxa de crescimento aumenta => diminui.
- Se a norma não muda e é constante => nós não mudamos.
- Se estiver abaixo do normal e cair e a taxa de queda aumentar => aumentar.
Todas as variáveis linguísticas nas regras são conectadas através dos blocos lógicos “e” e conectadas às saídas. Como pode ser visto na Figura 10, o circuito lógico de inferência fuzzy é praticamente diferente do circuito lógico usual, apenas blocos lógicos fuzzy são usados.
Semelhante ao ajuste do controlador PID, usamos o bloco de otimização.
A questão permanece com os parâmetros dos blocos.
Síntese de um controlador baseado em lógica nebulosa
Nada é dado na vida por nada e, portanto, a simplicidade das regras de regulamentação é compensada pelo número de parâmetros que descrevem as funções de associação. De fato, se você precisar selecionar três coeficientes para o controlador PID, no caso da lógica fuzzy, apenas uma função triangular precisará de 3 números para os vértices. Se para cada variável de entrada precisarmos de 3 funções de associação + 3 para a saída, será necessário definir 3 x 3 x 3 + 3 x 3 = 36 parâmetros!
Mas nem tudo é tão triste. Para uma primeira aproximação e configuração inicial, tudo pode ser simplificado.
Tendo feito algumas suposições para o ajuste inicial do controlador:
- Definimos a simetria das funções em relação a zero; em vez de dois números para o máximo e o mínimo, você pode especificar um - Max e, consequentemente, será definido como um intervalo [ -Max ... Max ].
- Definimos uma distribuição uniforme de funções, então podemos calcular a posição de todos os vértices dos triângulos com base em um determinado intervalo.
- Para três funções, as coordenadas dos vértices são definidas como –Max, 0, Máx.
- Definimos que a base do triângulo de todas as funções de associação é a mesma.
Assim, em vez de 36 parâmetros independentes, devemos especificar apenas 4, o desvio máximo de 0 para três variáveis de entrada e uma saída, a saber:
uMax - amplitude da ação de controle
(-uMax ... uMax) ;
deltaMax - desvio máximo
(-deltaMax ... deltaMax) ;
divMax - derivada máxima de desvio
(-divMax ... divMax) ;
div2Max - segunda derivada máxima do desvio
(-div2Max ... div2Max)Nas funções de fase e inferência fuzzy, usamos esses sinais para calcular os parâmetros levando em consideração as premissas aceitas.
Configurações do controlador propostas no livro por V.V. Gostev “Reguladores difusos em sistemas de modelagem automática”, para o caso de fase por três funções de associação, são propostos os seguintes parâmetros:
uMax = 30 - a amplitude da ação de controle;
deltaMax = 0,01 - desvio máximo;
divMax = 0,07 - derivada máxima do desvio;
div2Max = 1 é a segunda derivada máxima do desvio.
Comparação transitória
No gráfico de transientes, a coincidência de um determinado efeito e o resultado obtido são quase completos:

Figura 11.a Transitório. Controlador PID
| 
Figura 11.b Transitório. Lógica difusa
|
Diferenças óbvias podem ser vistas nos gráficos da ação de desvio e controle obtida:

Figura 12.a. Gerenciamento. Controlador PID
| 
Figura 12.b. Gerenciamento. Lógica difusa |
A partir da comparação das figuras, observa-se que o controlador difuso fornece menos erros e melhor transitório.
Vamos comparar os transitórios no sistema se definirmos uma ação de controle gradual. Os resultados na Figura 13:

Figura 13.a. Efeito passo. Controlador PID.
| 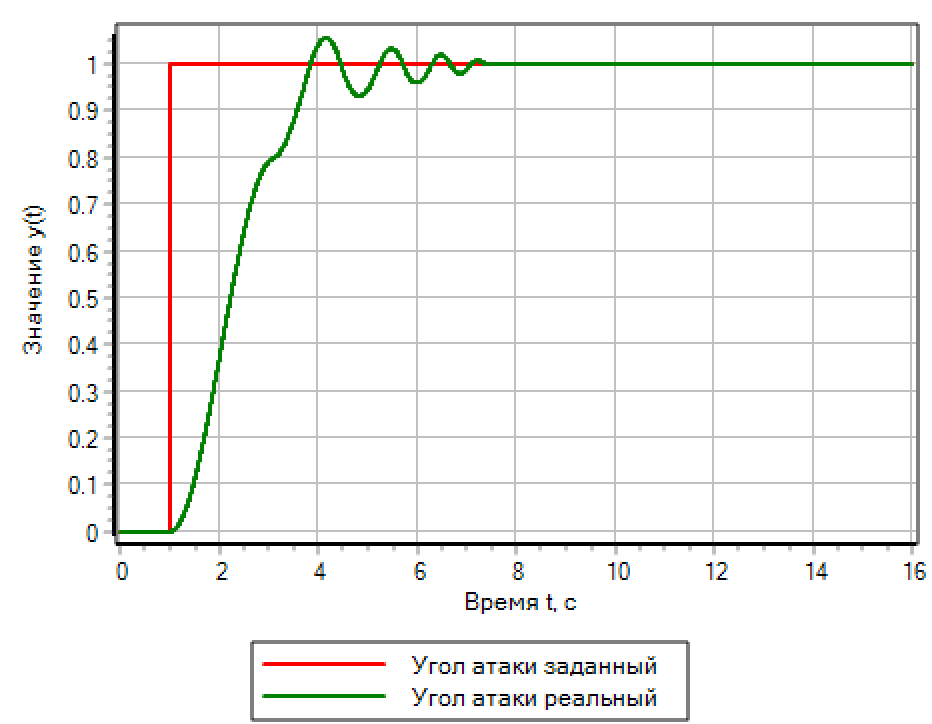
Figura 13.b. Efeito passo. Lógica difusa. |
Para ações passo a passo, um controlador baseado em lógica difusa fornece a melhor qualidade transitória. O controlador PID, que é definido automaticamente como um processo tranquilo, causa oscilações com excesso que são duas vezes a etapa definida.
Ajuste do controlador baseado em lógica nebulosa pelo método de otimização
Vamos tentar selecionar os parâmetros do controlador fuzzy pelo método de otimização, assim como os selecionamos para o controlador PID. Como critério, definimos o desvio padrão menor que 0,001.
Deve-se notar que esse método não é totalmente correto, porque para os profissionais é claro quais ângulos e quais velocidades são as máximas e mínimas para cada peça de concerto, o que permite definir restrições aos parâmetros otimizados de maneira mais consciente, definimos os parâmetros padrão e vemos o que acontece.
O método de otimização com configurações padrão calculou os seguintes valores dos intervalos de parâmetros de otimização:
uMax = 19.377 - a amplitude da ação de controle;
deltaMax = 1.095 - desvio máximo;
divMax = 0,01 - derivada máxima do desvio;
div2Max = 2.497 é a segunda derivada máxima do desvio.
No caso de uma otimização simples do desvio, os parâmetros obtidos fornecem a precisão especificada, no entanto, isso causa oscilações de alta frequência da ação de controle.
A função de transição e as ações de controle são apresentadas na Figura 14.a
 Figura 14.a. Lógica difusa. Configuração de desvio. Figura 14.a. Lógica difusa. Configuração de desvio.
| 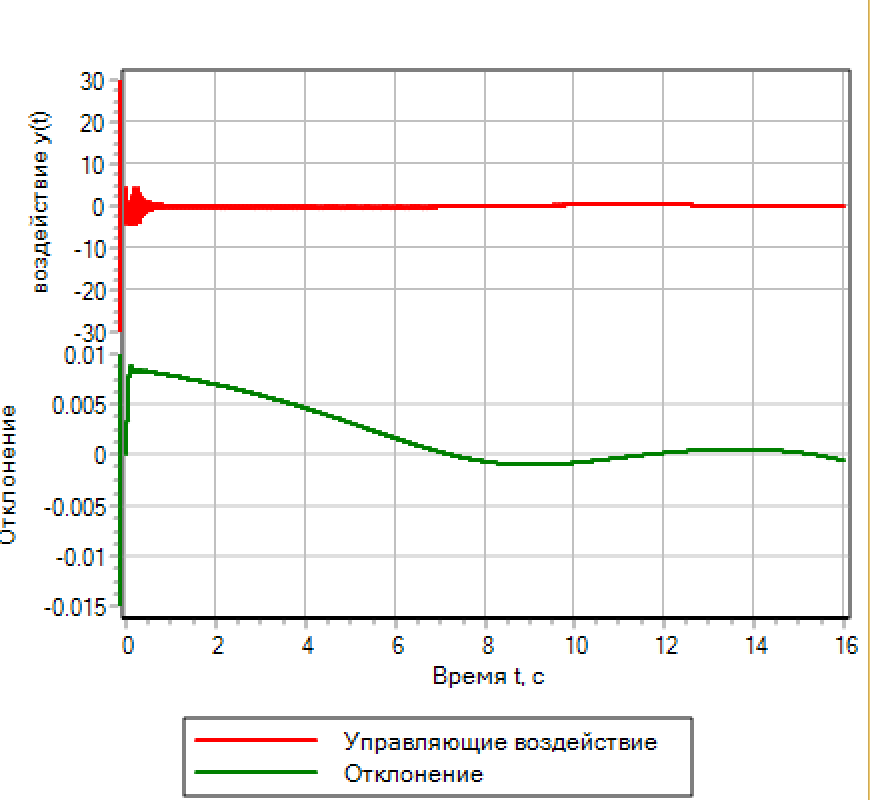 Figura 14.b. Lógica difusa. Configuração por desvio e número de respostas. Figura 14.b. Lógica difusa. Configuração por desvio e número de respostas. |
Para melhorar o processo transitório, pode-se adicionar ao critério de otimização o número de comutações do regulador do valor negativo para o positivo do efeito regulador (esquema na Fig. 15).
 Figura 15. Esquema para otimização por 2 critérios.
Figura 15. Esquema para otimização por 2 critérios.O cálculo pelo método de otimização de acordo com dois critérios fornece os seguintes valores de parâmetro:
uMax = 19.714 - a amplitude da ação de controle;
deltaMax = 1.0496 - desvio máximo;
divMax = 0,01 - derivada máxima do desvio;
div2Max = 1,7931 é a segunda derivada máxima do desvio.
Pode-se observar que, quando o número de disparos foi adicionado ao critério de otimização, foi possível reduzir a frequência de comutação do regulador (ver Fig. 14.b). Assim, podemos dizer que o método de otimização funciona mesmo quando não sabemos nada sobre a física do objeto e simplesmente selecionamos os parâmetros numéricos sem pensar em seu significado físico.
Criando seu próprio controlador com base na lógica difusa
Acima, criamos o controlador de acordo com um esquema já preparado e bastante simples, todos os termos de variáveis linguísticas foram conectados pelo operador lógico I. Como temos o mesmo número de termos nas entradas e saídas, esta é a solução mais simples e óbvia.
Vamos tentar criar um controlador cuja saída não tenha três termos, mas, por exemplo, 5:
reduzir rapidamente, reduzir, não mudar, aumentar, aumentar rapidamente . E na entrada o mesmo.
Vamos mudar a lógica do regulador, para iniciantes, simplificando o algoritmo de controle o máximo possível.Escrevemos as regras:1) Se é maior e cresce t => diminui rapidamente.2) Se mais => diminuir.3) Se a norma => não mudar.4) Se menor => aumentar.5) Se menos e têm menshaetsya => aumentar rapidamente.Nesse caso, temos 5 termos (5 funções triangulares) para a variável de saída. Aceitamos que eles sejam distribuídos igualmente entre -uMax e + uMax.Assumimos que as funções triangulares são compostas de tal maneira que quando as funções de associação do termo assumem valores máximos, as funções vizinhas assumem valores zero (veja a Fig. 5).Como parâmetros para a saída, apenas o desvio e a taxa de variação do desvio serão usados.Para acelerar os cálculos, usamos a fase de saída do método pelo centro de gravidade dos pontos (veja a Figura 7).O circuito do controlador, neste caso, será semelhante ao mostrado na Figura 15.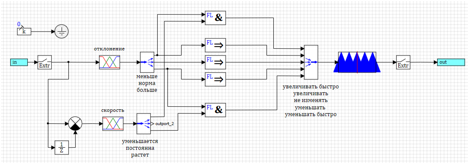 Figura 15. Um controlador simplificado baseado na lógica difusa.Em vez do intervalo da segunda derivada do otimizador, o valor para o termo "aumento" será obtido. Uma tentativa de ajustar esse regulador pelo método de otimização mostra que o regulador está ajustado, mas a qualidade da regulação do controle do sistema deixa muito a desejar.O melhor resultado é mostrado na Figura 16.
Figura 15. Um controlador simplificado baseado na lógica difusa.Em vez do intervalo da segunda derivada do otimizador, o valor para o termo "aumento" será obtido. Uma tentativa de ajustar esse regulador pelo método de otimização mostra que o regulador está ajustado, mas a qualidade da regulação do controle do sistema deixa muito a desejar.O melhor resultado é mostrado na Figura 16.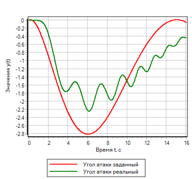 Figura 16. Transitório para um controlador simplificado.Pode-se ver que a regulamentação está ocorrendo, mas não de maneira alguma como gostaríamos. O fato é que exercemos o efeito quando um desvio já ocorreu. Vamos tentar ativar a regulamentação no momento em que temos um desvio na norma, mas a velocidade mostra que ela aumentará ou diminuirá.1) Se menos e diminui => aumenta rapidamente.2) Se a norma e aumenta => diminuem.3) Se a norma => não mudar.4) Se a norma e diminui => aumentam.5) Se maior e crescente => diminua rapidamente.
Figura 16. Transitório para um controlador simplificado.Pode-se ver que a regulamentação está ocorrendo, mas não de maneira alguma como gostaríamos. O fato é que exercemos o efeito quando um desvio já ocorreu. Vamos tentar ativar a regulamentação no momento em que temos um desvio na norma, mas a velocidade mostra que ela aumentará ou diminuirá.1) Se menos e diminui => aumenta rapidamente.2) Se a norma e aumenta => diminuem.3) Se a norma => não mudar.4) Se a norma e diminui => aumentam.5) Se maior e crescente => diminua rapidamente.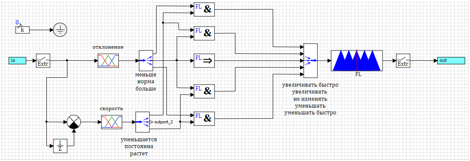 Figura 17. Controle pela taxa de variação do desvio.Os resultados da operação do controlador ajustado pelo método de otimização são apresentados nas Figuras 18a e 18b.
Figura 17. Controle pela taxa de variação do desvio.Os resultados da operação do controlador ajustado pelo método de otimização são apresentados nas Figuras 18a e 18b.
Figura 18.a. O processo de transição.
| 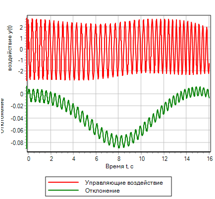
Figura 18.b. Gerência |
O controle sobre a taxa de variação do desvio melhorou significativamente o transitório. No entanto, se você examinar cuidadosamente o conjunto de regras lógicas, veremos que o desvio não está envolvido no gerenciamento. Se for dado um efeito de etapa, o controlador de controle não gerará uma ação de controle. A Fig. 19 mostra um exemplo de um processo transitório com uma ação de controle gradual, pode ser visto que o controlador não fornece uma ação de controle, embora o desvio seja 1.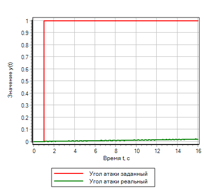
Figura 19.a. O processo de transição. Etapa
| 
Figura 19.b. Gerenciamento. Etapa |
Para calcular desvios rápidos, adicionamos uma ação de controle para desvios. Aumentaremos se menos e diminuiremos se mais. Como já existem regras no conjunto de regras sob as quais reduzimos e aumentamos, usamos o operador lógico ou:1) Se menos e diminui => aumenta rapidamente.2) Se ( norma e aumento ) ou mais => diminui.3) Se a norma => não mudar.4) Se ( norma e diminuição ) ou menos => aumenta.5) semaior e crescente => diminui rapidamente.O circuito do controlador de acordo com essas regras é apresentado na Figura 20.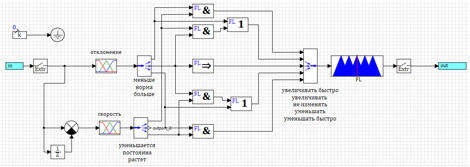 Figura 20. Um controlador com controle por desvio e taxa de variação.Como resultado da modificação, a qualidade do processo de transição com uma ação suave praticamente não mudou, no entanto, com uma ação passo a passo, o regulador começou a elaborar a etapa e trazer o ângulo de ataque do foguete para o especificado (veja a Fig. 21).
Figura 20. Um controlador com controle por desvio e taxa de variação.Como resultado da modificação, a qualidade do processo de transição com uma ação suave praticamente não mudou, no entanto, com uma ação passo a passo, o regulador começou a elaborar a etapa e trazer o ângulo de ataque do foguete para o especificado (veja a Fig. 21).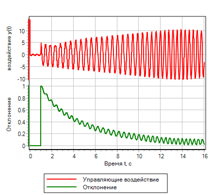
Figura 21.a. O processo de transição. Etapa
| 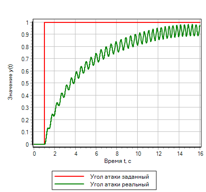
Figura 21.b. Gerenciamento. Etapa |
, «» .
, , . , , , .
, . , , . , , , :
1)
=> .2) (
)
=> .
3)
=> .4) (
)
=> .5)
=> .
22. «», , , «
& ».
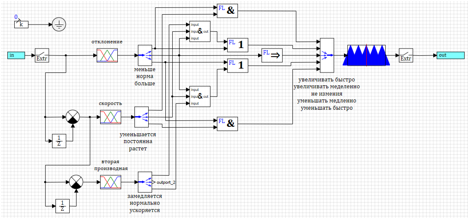 Figura 22. Controlador lógico difuso com controle da segunda derivada.Após a seleção dos parâmetros pelo método de otimização para o desvio e o número de inclusões, foram obtidos os seguintes parâmetros:uMax = 27.4983 - a amplitude da ação de controle;deltaMax = 0,0433 - desvio máximo;divMax = 0,0966 - derivada máxima do desvio;div2Max = 1.0828 - a segunda derivada máxima do desvio.O processo transitório é mostrado na Figura 23. É possível observar que o regulador resultante tem o melhor desempenho de todos os considerados acima, mas com um determinado efeito. Desvios e ações de controle são o mínimo de todos os considerados neste texto.
Figura 22. Controlador lógico difuso com controle da segunda derivada.Após a seleção dos parâmetros pelo método de otimização para o desvio e o número de inclusões, foram obtidos os seguintes parâmetros:uMax = 27.4983 - a amplitude da ação de controle;deltaMax = 0,0433 - desvio máximo;divMax = 0,0966 - derivada máxima do desvio;div2Max = 1.0828 - a segunda derivada máxima do desvio.O processo transitório é mostrado na Figura 23. É possível observar que o regulador resultante tem o melhor desempenho de todos os considerados acima, mas com um determinado efeito. Desvios e ações de controle são o mínimo de todos os considerados neste texto.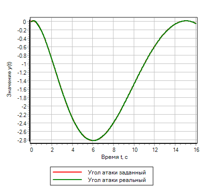
Figura 23.a. O processo de transição.
| 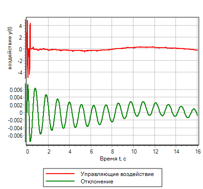
Figura 23.b. Gerenciamento. |
Conclusões
, -.
.
. .
, ,
...