1. Introdução
Para determinar as características balístico-temporais do movimento do centro de massa do paraquedista, é preciso escolher um modelo matemático simplificado, bastante acessível para a pesquisa analítica e, ao mesmo tempo, preservar as características mais características do objeto original.
Para construir modelos matemáticos simplificados do movimento do paraquedista, é realizada uma análise, determinação, sistematização de parâmetros constantes e de tempo.
Atualmente, não existem métodos regulares e suficientemente justificados para a construção de modelos matemáticos não lineares, para resolver problemas particulares, com a preparação correta dos sistemas iniciais de equações diferenciais não lineares, métodos numéricos para resolvê-los podem fornecer resultados bastante adequados.
O objetivo desta publicação é compilar e resolver numericamente sistemas de equações diferenciais que descrevem todos os estágios do movimento de um paraquedista pousando de um avião, levando em consideração o efeito das mudanças de altitude e temperatura da densidade de massa do ar.
Características balístico-temporais do movimento de um paraquedista
Parâmetros variáveis constantes e limitados incluem:
N é a altura do paraquedista;
V0 - velocidade da aeronave;
k - peso, altura do paraquedista;
g é a aceleração da gravidade;
ρ é a densidade do ar;
T é a temperatura do ar.
Parâmetros temporários (variáveis) incluem:
tn - hora de pouso,
w é a velocidade do vento;
V é a velocidade do paraquedista;
u é a velocidade dos fluxos ascendentes (descendentes);
d - desvio (distância da projeção ao solo do ponto de ejeção até o ponto de aterrissagem);
C é o coeficiente de arrasto do objeto de pouso;
F - seção média do objeto de pouso.
Estágios de salto
O primeiro estágio é uma queda livre após a separação da aeronave:
 O segundo estágio
O segundo estágio é uma diminuição de um pára-quedas estabilizador:

A principal propriedade do paraquedas estabilizador é a estabilização do paraquedista na posição mais conveniente para o paraquedas principal.
A terceira etapa - encher a cúpula do paraquedas principal:
 O quarto estágio
O quarto estágio é uma diminuição do paraquedas aberto:

Compilação de um sistema de equações diferenciais para todas as etapas do salto de paraquedas
Escolhemos um sistema de coordenadas fixo OXY centrado no ponto de ejeção O. O eixo OX coincide com a direção do componente horizontal da velocidade da aeronave. O eixo OY é direcionado verticalmente para cima na direção oposta à velocidade vertical do paraquedista.
Vamos assumir que o movimento do pára-quedista é plano e ocorre no plano OXY. Esse modelo de salto pode ser considerado um modelo de salto em clima calmo, sem levar em consideração a influência do vento.
Acreditamos que, além do peso, o paraquedista é afetado pela força da resistência do ar proporcional ao quadrado da velocidade do paraquedista:
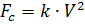
,
onde:
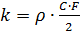
,
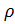
- densidade do ar, coeficiente de arrasto C, seção F do corpo.
Com o aumento da altura, a temperatura do ar muda:

A temperatura mínima já é atingida a uma altitude de 10 km. e é de -55 ° C. A densidade do ar também depende da pressão. Portanto, ao calcular a balística de um salto de para-quedas, é conveniente usar a seguinte fórmula para determinar a densidade do ar [1]:
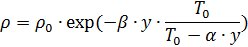
,
onde
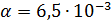
K / m;
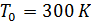
- temperatura ao nível do mar; y é a altura em m;

- densidade do ar em y = 0;
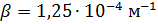
.
Na prática dos cálculos, o quadrado do crescimento é tomado como a seção mediana; o valor de C é encontrado na tabela [2]:

Θ indica o ângulo de inclinação da trajetória. Sob as suposições feitas para os componentes
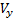
,
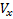
vetores de velocidade V, temos:

Dividindo por m os lados esquerdo e direito das equações do sistema resultante e denotando

através de r, obtemos:
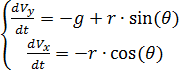
(1)
Escrevemos as equações de movimento de um pára-quedista na forma de um sistema de equações diferenciais para as funções V, θ, y (t), x (t).
Dado que:
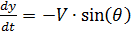
,
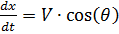
,
e tempo de diferenciação:

, levando em consideração o sistema de equações (1), obtemos:
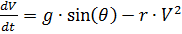
,
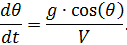
.
Assim, nas condições iniciais:
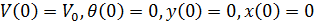
nós temos o seguinte sistema de equações diferenciais:
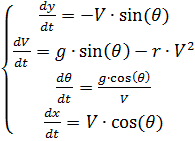
Solução numérica de um sistema de equações diferenciais (2) usando Python
Para resolver (2), reescrevemos da seguinte forma, introduzindo forças de arrasto estabilizadoras controladas pelo tempo e pela densidade do ar
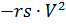
e principal
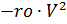
pára-quedas, respectivamente, multiplicados pelas funções de controle do tempo ks (t) e ko (t):
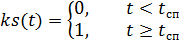
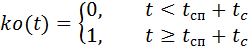
,
onde:
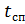
–– tempo de queda livre do paraquedista;

- o tempo de operação do pára-quedas de estabilização até a abertura do principal.
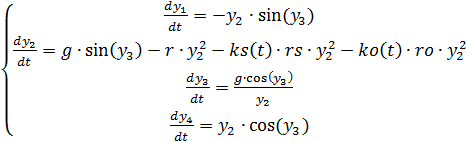
(3)
Lista completa do programa ajustado para alterações na densidade do ar Temos:
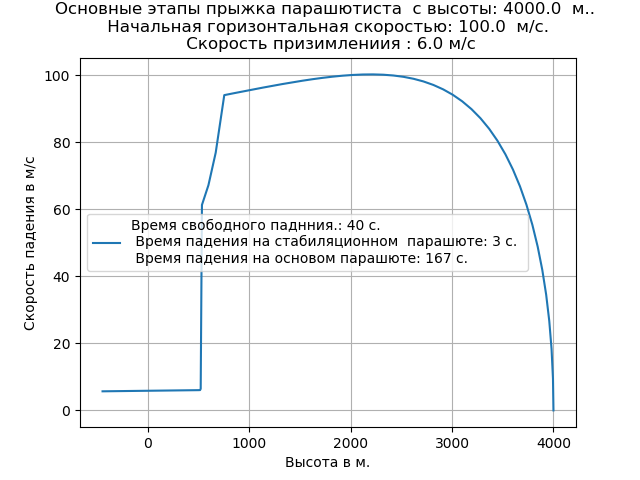
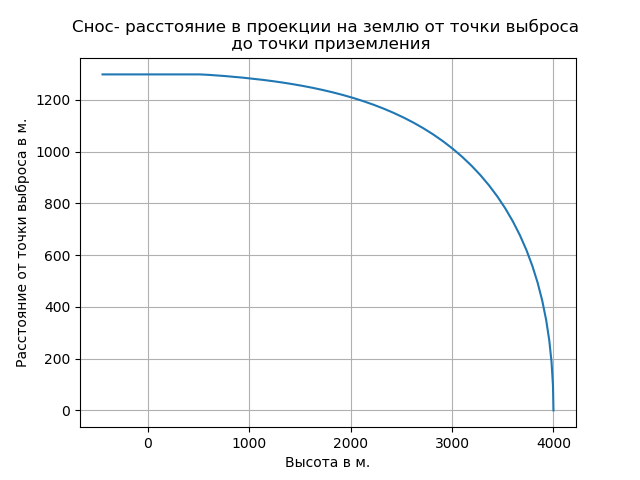
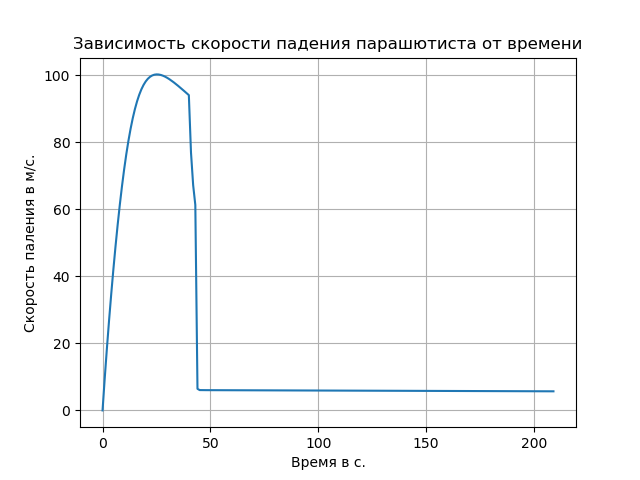
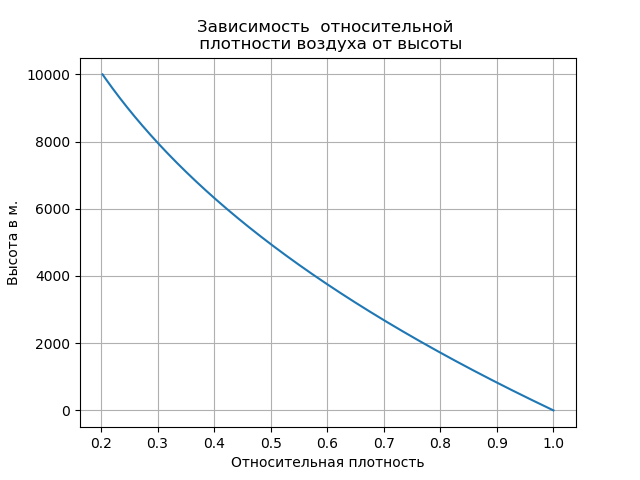
Levar em consideração o ar rarefeito levou a um aumento na taxa de queda livre e mudou a natureza da trajetória nesta seção.
Este problema pode ser resolvido com a ajuda de um sistema de duas equações diferenciais, que são dadas abaixo (excluindo pára-quedas e alterações na densidade do ar):
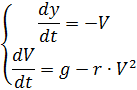
A mudança nas forças de resistência e na densidade do ar é mostrada na lista abaixo do spoiler, levando em consideração o exposto acima e sem explicações# - * - codificação: utf8 - * -
de importação numpy *
de scipy.integrate import odeint
importar matplotlib.pyplot como plt
m = 100
r0 = 1,3
c1 = 0,3
c2 = 0,6
c3 = 0,5
c4 = 0,75
S = 70
s = 0,8
ss = 1,5
g = 9,8
colher de chá = 6
tsbp = 10
tp = 90,0
h = 1000.0
beta = 1,25 * 10 ** - 4
alfa = 6,5 * 10 ** - 3
T0 = 300
def ks (t):
se t <tsp:
z = 0
mais:
z = 1
retornar z
def ko (t):
se t <tsp + tsbp:
z = 0
mais:
z = 1
retornar z
# dy1 / dt = y2
# dy2 / dt = g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S
return [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = arange (0,0, tp)
y0 = [h, 0,0]
[y1, y2] = nó (f, y0, t, saída_computador = Falso) .T
plt.title ("Paraquedismo de 1000 e 800 metros")
plt.plot (y1, y2, label = 'Altitude 1000 m')
h = 800,0
colher de chá = 6
tsbp = 2
tp = 80,0
def ks (t):
se t <tsp:
z = 0
mais:
z = 1
retornar z
def ko (t):
se t <tsp + tsbp:
z = 0
mais:
z = 1
retornar z
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0,5 * r * c1 * s
k2 = 0,5 * r * c2 * s
k3 = 0,5 * r * c3 * ss
k4 = 0,5 * r * c4 * S
return [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = arange (0,0, tp)
y0 = [h, 0,0]
[y1, y2] = nó (f, y0, t, saída_computador = Falso) .T
plt.plot (y1, y2, label = 'Altura 800 m')
plt.xlabel ('Altura em metros')
plt.ylabel ('Velocidade de gravação em m / s.')
plt.legend (loc = 'melhor')
plt.grid (True)
plt.show ()
Temos:

Conclusão
São determinadas as características balístico-temporais do movimento do centro de massa de um paraquedista que aterra de um avião.
Referências
- Pressão atmosférica.
- Gerasimenko I.A. Treinamento aéreo: livro didático. M: Military Publishing, 1986. Parte 1, p. 32.