Oi Habr. Hoje eu gostaria de desenvolver o tópico da
otimização variacional e dizer como aplicá-lo à tarefa de aparar canais não informativos em redes neurais (poda). Utilizando-o, é possível aumentar de forma relativamente fácil a "taxa de incêndio" de uma rede neural sem remover sua arquitetura.
A idéia de reduzir elementos redundantes nos algoritmos de aprendizado de máquina não é nada nova. De fato, é mais antigo que o conceito de aprendizado profundo: foi apenas anteriormente que galhos de árvores decisivas foram cortados e agora pesam em uma rede neural.
A idéia básica é simples: encontramos na rede um subconjunto de pesos inúteis e os zero. Sem uma pesquisa exaustiva, é difícil dizer quais pesos realmente participam da previsão e quais apenas fingem, mas isso não é necessário. Vários métodos de regularização, dano cerebral ideal e outros algoritmos funcionam bem. Por que remover todos os pesos? Acontece que isso melhora a capacidade de generalização da rede: em geral, pesos insignificantes simplesmente introduzem ruído na previsão ou são especialmente aprimorados para sinais de um conjunto de dados de treinamento (ou seja, um artefato de reciclagem). Nesse sentido, a redução de conexões pode ser comparada com o método de desconectar neurônios aleatórios (abandono) durante o treinamento em rede. Além disso, se a rede tiver muitos zeros, ela ocupa menos espaço no arquivo e pode ler mais rapidamente em algumas arquiteturas.
Parece bom, mas é muito mais interessante jogar não pesos separados, mas neurônios de camadas ou canais totalmente conectados de todos os feixes. Nesse caso, o efeito da compactação da rede e da aceleração das previsões é observado com muito mais clareza. Mas isso é mais complicado do que destruir pesos individuais: se você tentar realizar o dano cerebral ideal, pegando todo o pacote em vez de uma conexão, os resultados provavelmente não serão muito impressionantes. Para poder remover um neurônio sem dor, é necessário fazê-lo para que ele não tenha uma única conexão útil. Para fazer isso, você precisa induzir de alguma forma os neurônios "fortes" a se tornarem mais fortes e os "fracos" a se tornarem mais fracos. Essa tarefa já é familiar para nós: de fato, forçamos a rede a ser esparsa, induzindo com algumas restrições ao agrupamento de pesos.
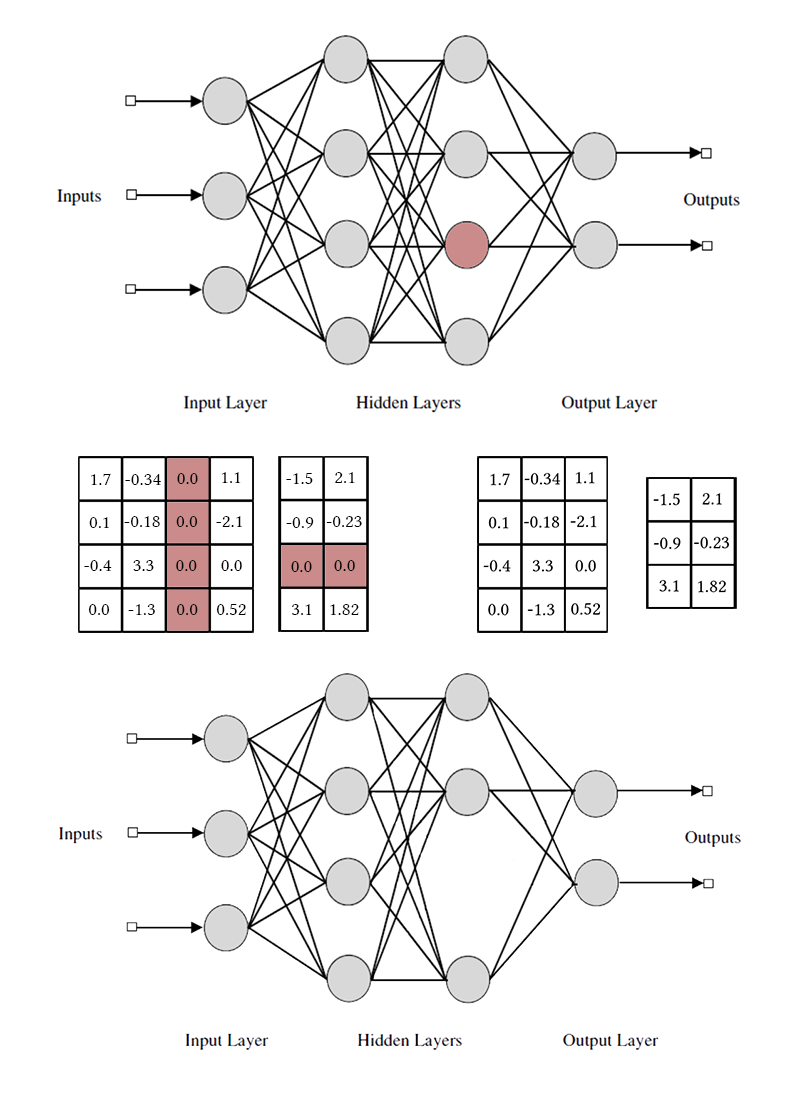
Observe que, para remover um neurônio ou canal convolucional, é necessário modificar duas matrizes de pesos. Não vou distinguir entre canais convolucionais e neurônios: o trabalho com eles é o mesmo, apenas os pesos específicos removidos e o método de transposição diferem.
O caminho mais fácil: regularização do grupo L1
Para começar, vou falar sobre a maneira mais simples e eficaz de remover neurônios extras da rede - regularização em grupo LASSO. Na maioria das vezes, é usado para manter pesos inúteis em redes próximas a zero; generaliza trivialmente para o caso de canal por caso. Ao contrário da regularização regular, não regularizamos diretamente a ativação do peso ou da camada, a ideia é um pouco mais complicada. [Poda de canal para acelerar redes neurais muito profundas; Yihui He et al; 2017]
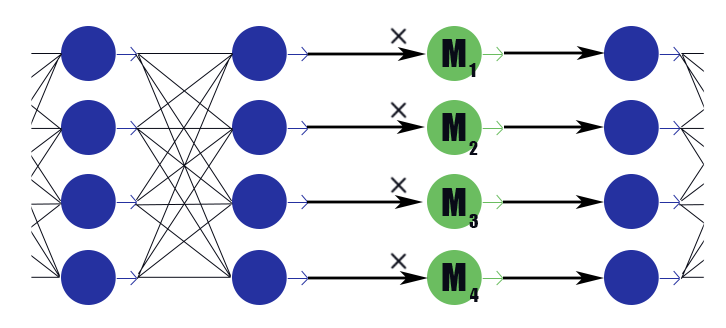
Considere uma camada de máscara especial com um vetor de peso
M=( beta1, beta2, dots, betan) . Sua conclusão é apenas um trabalho por partes
M para as conclusões da camada anterior, ele não tem função de ativação. Colocamos na camada de máscara após cada camada, os canais nos quais queremos descartar, e sujeitamos os pesos nessas camadas à regularização de L1. Assim, o peso da máscara
betai multiplicado pela i-ésima saída da camada impõe implicitamente uma restrição a todos os pesos dos quais essa conclusão depende. Se entre esses pesos, digamos meio útil, então
betai permanecerá mais próximo da unidade e esta conclusão será capaz de transmitir bem as informações. Mas se apenas um ou nenhum,
betai cairá para zero, o que redefinirá a saída do neurônio e, de fato, redefinirá todos os pesos dos quais essa conclusão depende (no caso da função de ativação igual a zero em zero). Observe que dessa forma a rede recebe menos reforços negativos no caso de um peso legalmente grande ou de uma resposta juridicamente forte. A utilidade do neurônio como um todo é importante.
Acontece esta fórmula:
Onde
lambda - constante de ponderação de perda 'uma rede e perda' uma escassez. Parece com a fórmula usual de regularização L1, apenas o segundo termo contém vetores de camadas de máscara, e não o peso da rede.
Após o treinamento da rede, examinamos os neurônios e seus valores mascarados. Se
betai mais do que um certo limiar, os pesos dos neurônios são multiplicados por
betai se menor, os elementos correspondentes ao neurônio são removidos das matrizes dos pesos de entrada e saída (como na figura um pouco mais alta). Depois disso, as máscaras podem ser descartadas e a rede concluída.
Na aplicação do grupo LASSO, existem várias sutilezas:
- Regularização normal. Juntamente com a regularização dos pesos da máscara, a regularização L1 / L2 deve ser aplicada a todos os outros pesos da rede. Sem isso, uma diminuição no peso de mascaramento no caso de funções de ativação não saturadas (ReLu, ELu) será facilmente compensada por um aumento nos pesos, e o efeito de anulação não funcionará. Sim, e para o sigmoide comum, isso permite que você inicie melhor o processo com feedback positivo: Mi a saída não informativa se torna menor, e é por isso que o otimizador precisa pensar mais fortemente sobre cada peso específico, o que torna a saída ainda mais informativa, e é por isso que Mi diminui ainda mais e assim por diante.
- Os autores do artigo também aconselham a impor uma restrição esférica ao peso das camadas |Wi|2=1 . Provavelmente, isso deve contribuir para o "fluxo" do equilíbrio de neurônios fracos para fortes, mas não notei muita diferença.
- Treinamento push-pull. Os autores do artigo sugerem o treinamento alternativo dos pesos normais da rede neural e dos pesos de máscara. É mais longo do que ensinar tudo de uma vez, mas como se os resultados fossem um pouco melhores?
- Não se esqueça do longo ajuste fino da rede (ajuste fino) após a correção da máscara, isso é muito importante.
- Monitore cuidadosamente como estão as suas máscaras: antes ou depois da função de ativação. Você pode ter problemas com ativações que não são iguais a zero quando o argumento é zero (por exemplo, um sigmóide).
- A remoção não é compatível com a batchnorm pela mesma razão que a desistência não é amigável com ela: do ponto de vista da normalização, quando há 32 valores no pacote 32, dos quais 12 são zero e quando 20 valores no pacote são situações muito diferentes. Depois de extrair o saldo zerado, a distribuição aprendida pela camada batchnorm deixa de ser válida. Você precisa inserir camadas de remoção após todas as camadas batchnorm ou modificar de alguma forma a última.
- Também há dificuldades em aplicar a redução de canal a arquiteturas de ramificação e redes residuais (ResNet). Após aparar neurônios extras durante a fusão de galhos, as dimensões podem não coincidir. Isso é facilmente resolvido pela introdução de camadas tampão, nas quais não rejeitamos neurônios. Além disso, se as ramificações da rede transportam uma quantidade diferente de informações, faz sentido definir diferentes lambda para que não aconteça que a poda apenas corte todos os neurônios no ramo menos informativo. No entanto, se todos os neurônios são cortados, esse ramo não é tão importante?
- Na declaração original do problema, há uma restrição estrita no número de canais diferentes de zero, mas, na minha opinião, basta alterar apenas os parâmetros de ponderação da perda inicial e da perda L1 dos pesos de máscara e, em seguida, deixar o otimizador decidir quantos canais serão deixados.
- Capture máscaras. Isso não está no artigo original, mas, na minha opinião, esse é um bom mecanismo prático para melhorar a convergência. Quando o valor da máscara atinge um determinado valor baixo predeterminado, nós o redefinimos e proibimos a alteração desta parte da máscara. Assim, pesos fracos deixam completamente de contribuir para a previsão já durante o treinamento do modelo e não introduzem nenhum valor perdido nos valores correspondentes. Teoricamente, isso pode impedir que um canal potencialmente útil retorne ao serviço, mas não acho que isso esteja acontecendo na prática.
Da maneira mais difícil: regularização L0
Mas não estamos procurando maneiras fáceis, certo?
A rejeição de canal usando a regularização L1 não é totalmente justa. Permite que o canal se mova na escala de "resposta forte" - "resposta fraca" - "resposta zero". Somente quando o peso da máscara está próximo o suficiente de zero, descartamos o canal usando a máscara de captura. Esse movimento distorce bastante a imagem e faz alterações em outros canais durante o treinamento: antes que eles possam aprender o que fazer quando o neurônio anterior estiver completamente desligado, devem aprender o que fazer quando sistematicamente der uma resposta fraca.
Deixe-me lembrá-lo de que, idealmente, gostaríamos de selecionar ansiosamente o canal menos informativo da rede, continuar aprendendo a rede sem ele, excluir o próximo canal menos informativo, ajustar a rede novamente e assim por diante. Infelizmente, nessa formulação, a tarefa é insuportável computacionalmente, mesmo para redes relativamente simples. Além disso, essa abordagem não deixa os canais uma segunda chance - uma vez que um neurônio remoto não pode retornar à operação novamente. Vamos mudar um pouco a tarefa: algumas vezes removemos o neurônio e, às vezes, o deixamos. Além disso, se o neurônio como um todo é útil, ele é deixado com mais frequência, mas se for inútil - vice-versa. Para isso, usaremos as mesmas camadas de máscara que no caso da regularização L1 (não foi sem razão que elas foram introduzidas!). Somente seus pesos não se moverão ao longo de todo o eixo real com o atrator em zero, mas serão concentrados em torno de 0 e 1. Não que tenha se tornado muito mais simples, mas pelo menos resolvido o problema da remoção categórica dos neurônios.
O instinto do instrutor de rede sugere que não é necessário resolver o problema através de uma pesquisa exaustiva, mas você precisa adicionar o número de neurônios ativos nas camadas na execução atual à função de perda. No entanto, esse termo em perda será gradualmente constante, e a descida em gradiente não poderá funcionar com ele. É necessário, de alguma forma, ensinar o algoritmo de aprendizado a excluir periodicamente alguns neurônios, apesar da ausência de gradiente.
Temos uma maneira de remover temporariamente os neurônios: podemos aplicar um abandono à camada da máscara. Deixe durante o treinamento
betai=1 com probabilidade
pi e
betai=0 com probabilidade
1− pi . Agora, na função de perda, você pode colocar a soma
pi que é um número real. Aqui estamos diante de outro obstáculo: a distribuição é discreta, não está claro como a retropropagação funciona com ela. Em geral, existem algoritmos especiais de otimização que podem nos ajudar aqui (consulte REFORÇAR), mas adotaremos uma abordagem diferente.
E então chegou o momento em que a
otimização variacional entra em
jogo : podemos aproximar a distribuição discreta de zeros e uns na camada de máscara por uma contínua e otimizar os parâmetros deste último usando o algoritmo de retropropagação usual. Essa é a idéia por trás do trabalho [Aprendendo Redes Neurais Esparsas Através da Regularização de L0; Christos Louizos et al; 2017].
O papel da distribuição contínua será desempenhado pela distribuição de concreto rígido [A Distribuição de Concreto: Um Relaxamento Contínuo de Variáveis Aleatórias Discretas; Chris Maddison; 2017], aqui está uma coisa tão complicada dos logaritmos que se aproxima da distribuição de Bernoulli:
alpha - distribuição deslocada em relação ao centro, e
beta - temperatura. At
beta rightarrow0 cada vez mais, a distribuição começa a aproximar-se da verdadeira distribuição de Bernoulli, mas perde sua diferenciabilidade. At
0< beta<1 a densidade de distribuição é côncava (é o caso em que estamos interessados), por
beta>1 - convexo. Passamos essa distribuição por um sigmóide rígido, para que ele possa ceder com uma probabilidade finita diferente de zero
z=0 e
z=1 , e no intervalo (0, 1) havia uma densidade diferenciável contínua. Depois de terminar a poda, examinamos em que direção a distribuição mudou e substituímos a variável aleatória
z para um valor de máscara específico
beta e trazemos à condição um modelo já determinístico.
Para sentir uma distribuição um pouco melhor, darei alguns exemplos de sua densidade para diferentes parâmetros:
Densidade de distribuição a l p h a = 0 , 0 , b e t a = 0 , 8 :
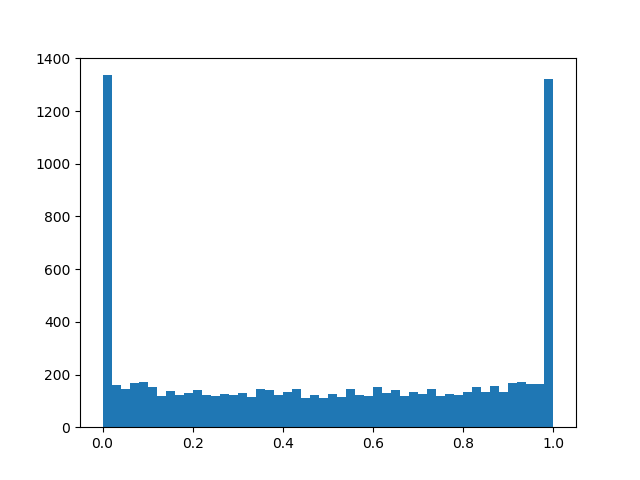 alpha=1,0, beta=0,8
alpha=1,0, beta=0,8 :
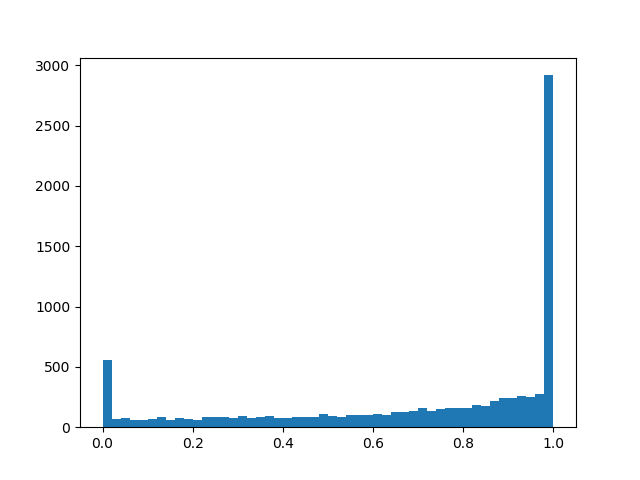 alpha=2,0, beta=0,8
alpha=2,0, beta=0,8 :
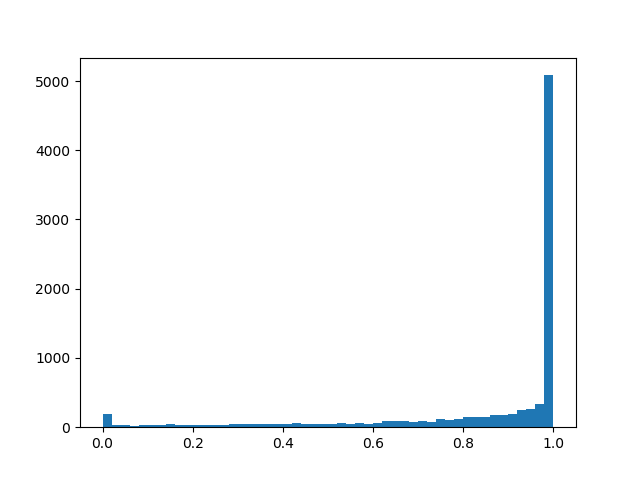 alpha=0,0, beta=0,5
alpha=0,0, beta=0,5 :
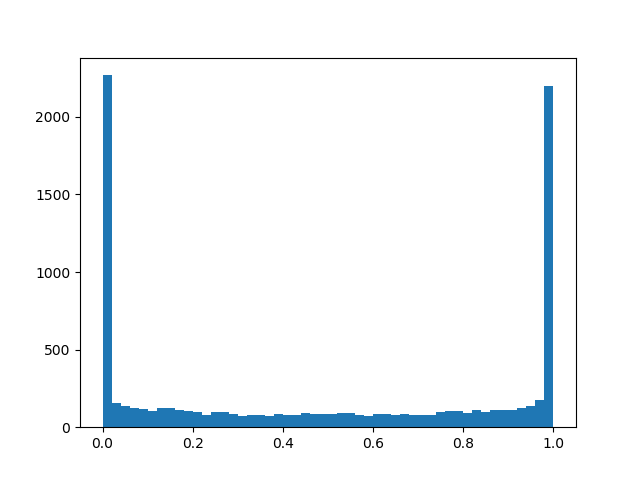 alpha=1,0, beta=0,5
alpha=1,0, beta=0,5 :
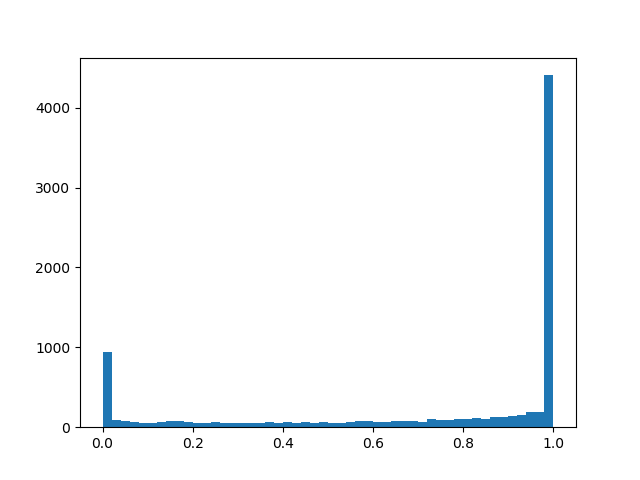 alpha=2,0, beta=0,5
alpha=2,0, beta=0,5 :
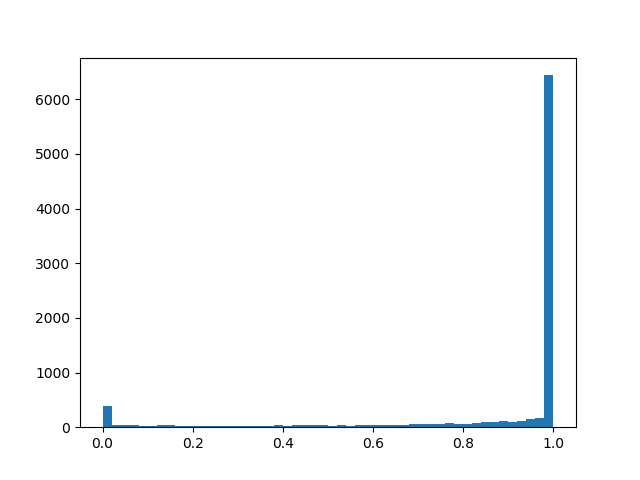 alpha=2,0, beta=0,1
alpha=2,0, beta=0,1 :
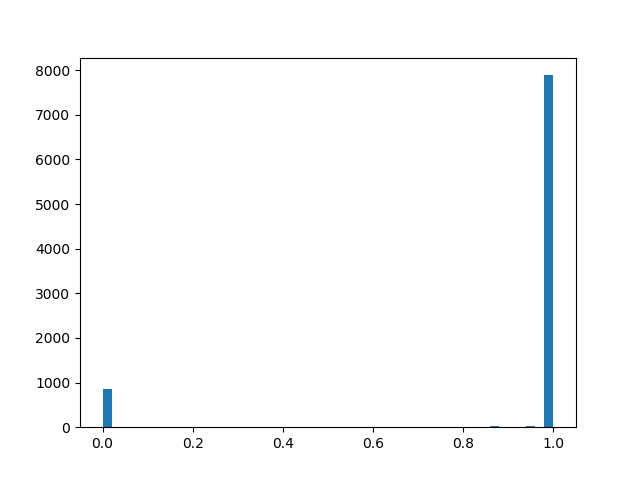 alpha=2,0, beta=2,0
alpha=2,0, beta=2,0 :
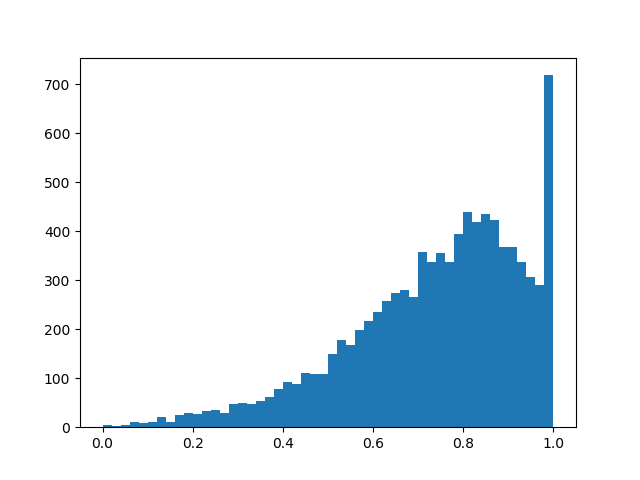
Em essência, temos uma camada de evasão "inteligente" que aprende quais conclusões devem ser descartadas com mais frequência. Mas o que exatamente estamos otimizando? Na perda, você deve colocar a integral da densidade de distribuição em uma região diferente de zero (a probabilidade de que a máscara se torne diferente de zero durante o treinamento, basta colocar):
Os seguintes recursos foram adicionados ao treinamento push-pull, regularização regular e outros detalhes de implementação mencionados no capítulo sobre regularização L1:
- Mais uma vez: nossa camada "inteligente" de abandono com alguma probabilidade perceptível redefine a saída, com algumas - deixa como está e, além disso, há uma pequena chance, dependendo da beta, xi, gama que a saída será multiplicada por um número aleatório de 0 a 1. A última parte é mais parasitária do que útil para nosso objetivo final, mas sem ela de forma alguma - é necessária para a retropropagação 'um passback.
- Geralmente e alpha e beta - parâmetros de treinamento, mas em meus experimentos senti que, se você apenas perguntar um pouco beta (0,05) e no processo de aprendizado ainda é linearmente reduzido, o algoritmo converge melhor do que se você o aprender honestamente. alpha é melhor definir grande o suficiente log alpha aproximadamente2,5 de modo que, inicialmente, os neurônios são mais frequentemente preservados do que descartados, mas não grandes o suficiente para saturar o sigmóide nas perdas.
- Se substituído em fórmulas log alpha apenas alpha como se a rede estivesse convergindo melhor e com menos probabilidade de encontrar o NaN durante o treinamento. Com esta manobra, não se deve esquecer de alterar o termo na função de perda e inicialização.
- Além disso, se você trapacear e substituir o sigmóide usual em perda por um rígido com restrições de log alpha em[−4,4] , a regularização convergirá melhor e agirá com mais força.
- Para alpha e beta Além disso, você pode aplicar a regularização para aumentar ainda mais a escassez.
- Após o treinamento, você deve binarizar os resultados e treinar persistentemente a rede com a máscara determinada até que a precisão val alcance a constante. O artigo fornece uma fórmula mais precisa pela qual a saída de um neurônio pode ser tornada determinística durante a validação ou a liberação de uma rede, mas parece que até o final do treinamento alpha acabam polarizados o suficiente para que uma heurística simples funcione: alpha<0 - máscara 0, a l p h a g e q 0 - máscara 1 (mas isso não é exato). Depois de passar para as máscaras determinísticas, você verá um salto na qualidade. Não se esqueça de que chegamos aqui com peso zero e, abaixo de um certo limite de peso, você ainda precisa substituir os pesos de máscara por zeros.
- Uma vantagem adicional da abordagem L0 - as camadas de máscara começam a funcionar como um abandono, o que traz um poderoso efeito de regularização para a rede. Mas esta é uma faca de dois gumes: se você começar a treinar com muito pouco a l p h a Existe o risco de arruinar a estrutura de rede pré-treinada.
Os experimentos
Para o experimento, vamos pegar o conjunto de dados CIFAR-10 e uma rede relativamente simples de quatro camadas convolucionais, seguidas por duas totalmente conectadas: Conv2D, Máscara, Conv2D, Máscara, Pool2D, Conv2D, Máscara, Conv2D, Máscara, Pool2D, Achatar, Abandono (p = 0,5) , Denso, Máscara, Denso (logits). Acredita-se que os algoritmos de poda funcionam melhor em redes mais espessas, mas aqui me deparei com um problema puramente técnico de falta de poder de computação. Como otimizador, Adam foi utilizado com uma taxa de aprendizado = 0,0015 e tamanho do lote = 32. Além disso, as regularizações habituais de L1 (0,00005) e L2 (0,00025) foram usadas. O aumento da imagem não foi aplicado. A rede foi treinada 200 épocas antes da convergência, após a qual foi preservada, e algoritmos de redução de neurônios foram aplicados a ela.
Além de aplicar os algoritmos descritos acima para remoção, definimos um ponto de referência trivial para garantir que os algoritmos façam alguma coisa. Vamos tentar jogar fora o primeiro de cada camada
k neurônios e acabar com a rede resultante.
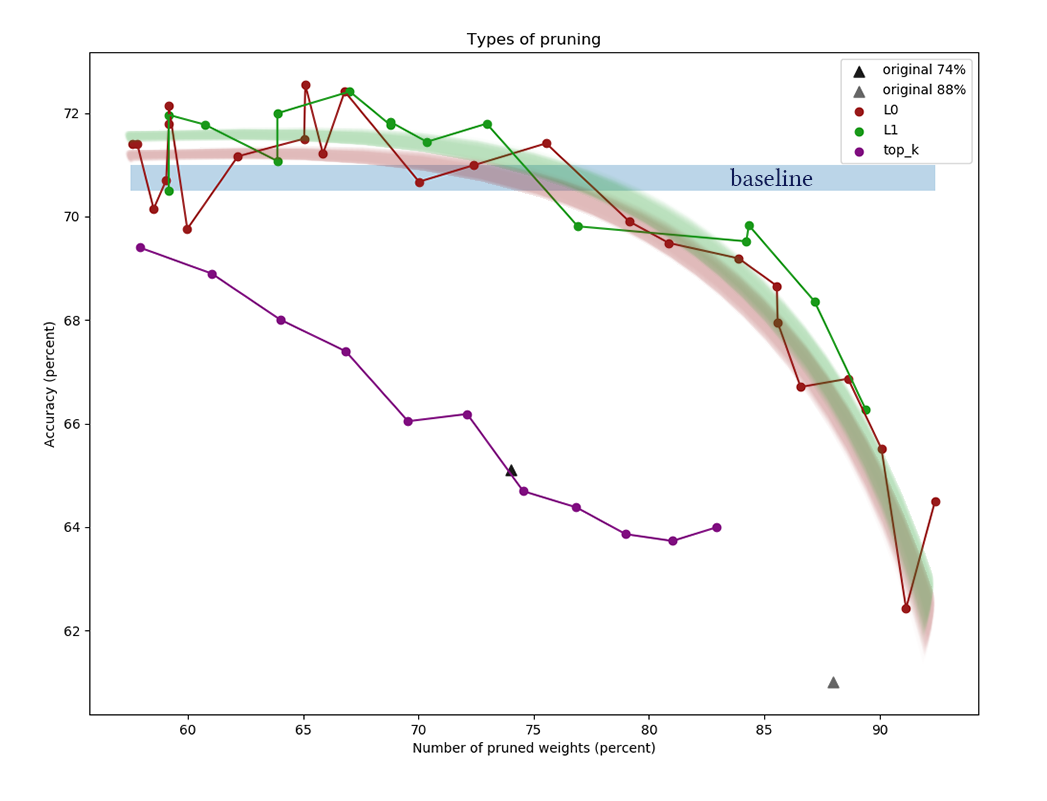
O gráfico mostra os resultados da comparação dos algoritmos de redução de canal L1 e L0 após uma série de experimentos com diferentes constantes de potência de regularização. O eixo x
representa a redução percentual no número de
pesos após a aplicação do algoritmo. No eixo Y, a precisão da rede de corte na amostra de validação. A barra azul no meio é a qualidade aproximada de uma rede que ainda não foi cortada de neurônios. A linha verde representa um algoritmo simples de aprendizado de máscara L1. A linha vermelha é poda de L0. Linha roxa - primeira remoção
k canais. Triângulos pretos - treinando uma rede que inicialmente tinha menos pesos.
Outro exemplo para o CIFAR-100 e uma rede um pouco mais longa e mais ampla, aproximadamente da mesma arquitetura e com parâmetros de treinamento semelhantes:
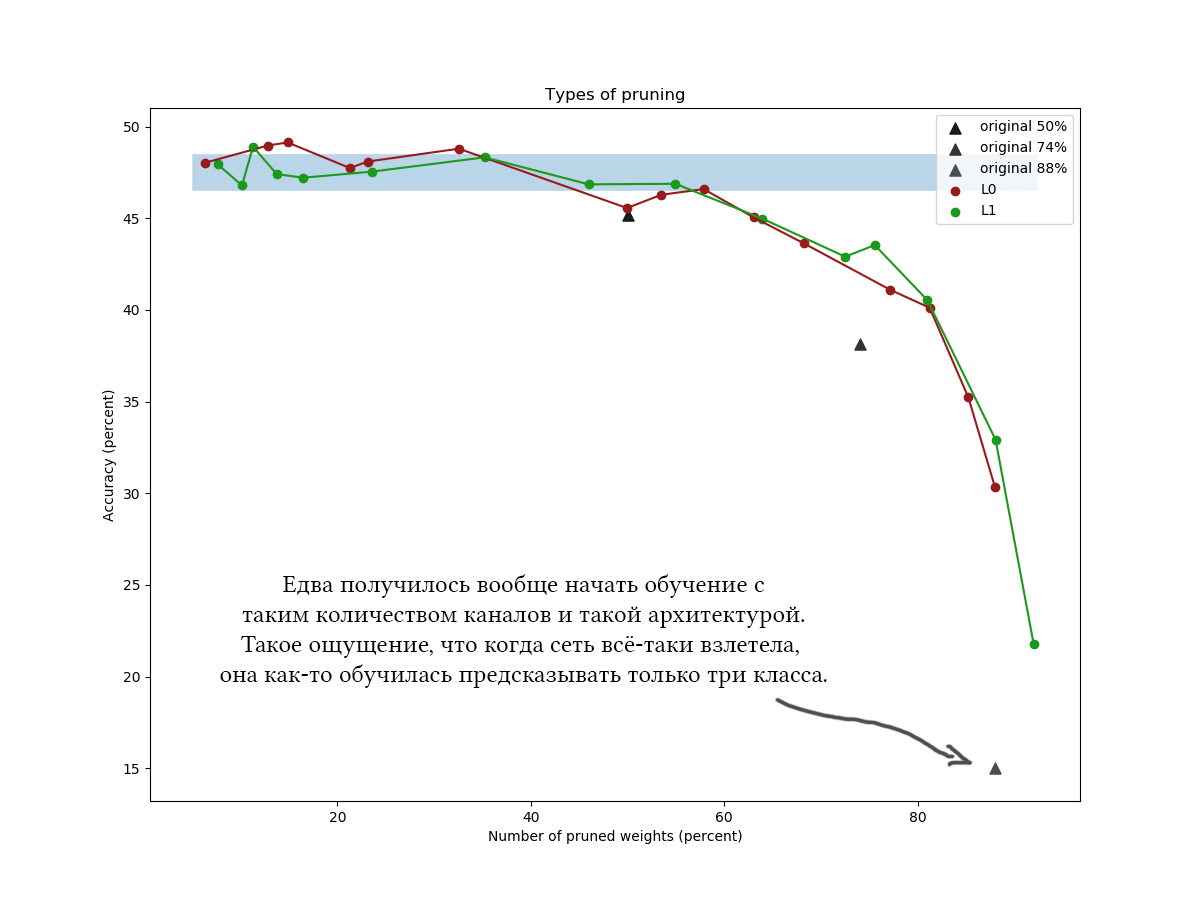
Nos gráficos, é claramente visível que um algoritmo L1 simples lida com a otimização variacional astuta e parece que até melhora a qualidade da rede um pouco mais com baixos valores de compactação. Os resultados também são confirmados por experimentos únicos com outros conjuntos de dados e arquiteturas de rede. Esse é um resultado absolutamente esperado, com o qual contei quando iniciei experimentos sobre redução de rede. Sinceramente. Suspiro.
Bem, para ser sincero, fiquei um pouco surpreso e tentei brincar com o algoritmo e a rede: diferentes arquiteturas, hiperparâmetros de rede, fórmulas exatas, distribuição de concreto duro, valores iniciais
a l p h a e
b e t a , o número de épocas de ajuste intermediário. A regularização de L0 parece legal na teoria, mas na prática é mais difícil escolher hiperparâmetros e leva mais tempo, portanto, eu não recomendaria usá-lo sem experimentos adicionais e processamento de arquivos. Por favor, não considere o tempo gasto lendo o artigo: a poda de L0 parece realmente muito crível, e eu diria que preferi aplicar o algoritmo em algum lugar incorretamente, que não recebi o ganho prometido. Além disso, a otimização variacional é a base para algoritmos de redução ainda mais avançados [por exemplo, Compressing Neural Networks using the Variational
Gargalo de informações, 2018].Em geral, as seguintes conclusões podem ser tiradas:- . 30-50% . «» , . [The Lottery Ticket Hypothesis: Training Pruned Neural Networks, J. Frankle and M. Carbin, 2018] ( , , , ).
- , . . , ?
- , . 60-90% . k <7%, .
- , (<60%) : , !
- L1 L0 (APoZ), , .. , k .
- , . , , , , . , , . pruning' , . - , .
Lembre-se de como eu escrevi no início do post que, depois de concluir o algoritmo de verificação, você pode "apenas cortar completamente as partes extras da rede"? Portanto, cortar partes extras da rede não é nada fácil. O fluxo de tensão e outras bibliotecas constroem um gráfico computacional e não pode ser alterado tão facilmente quando já está em operação. É necessário salvar a rede com as máscaras calculadas, extrair a lista dos pesos necessários, transpor os pesos conforme necessário, excluir os grupos zerados, transpor de volta e criar uma nova rede com base no conjunto de tensores de saída. A rede resultante deve ter o mesmo layout que o original, mas terá menos neurônios. Espere uma dor de cabeça ao manter o mesmo esquema de rede na função de criar a rede inicial e final, especialmente se elas não forem lineares, mas ramificadas.Provavelmente, para uma máscara conveniente, você deve criar suas próprias camadas. É fácil, mas tome cuidado com as coleções às quais você adiciona opções de máscara. É fácil cometer um erro e treinar acidentalmente os parâmetros de redução de canal, juntamente com todas as outras escalas.Deve-se notar que uma parte significativa do peso das redes com arquiteturas não muito profundas geralmente se concentra na transição de uma parte convolucional para uma totalmente conectada. Isso se deve ao fato de a última camada convolucional ser plana, como resultado, por assim dizer, (número de canais) * (largura) * (altura) dos neurônios, e a próxima matriz de pesos é muito ampla. É improvável que esses pesos sejam cortados; além disso, isso não deve ser feito, caso contrário, as últimas camadas da rede ficarão "cegas" para os recursos encontrados em alguns lugares. Nesses casos, tente diminuir o número final de canais e use maxpool'ing ou até mesmo arquiteturas totalmente convolucionais ou totalmente conectadas.Obrigado a todos por sua atenção, se alguém estiver interessado em repetir as experiências no CIFAR-10 e CIFAR-100,o código pode ser obtido no github . Tenha um bom dia de trabalho!