1. Introdução

Esta breve nota falará sobre como o modelo de dispersão da luz atmosférica está estruturado em nosso último 4k int Appear by Jetlag , cuja versão em festa conquistou um 12o lugar honroso na introdução da composição em 4k na festa de demonstração Revision 2018 em abril deste ano.

Você pode baixar o binário gratuitamente sem SMS aqui .

Se, no entanto, você não possui Windows ou se não possui uma placa de vídeo moderna e poderosa, existe um tolo reconfortante:

A música para este trabalho foi escrita por keen usando 4klang . Todo o código e recursos visuais ficaram para trás.

Aqui vamos falar apenas sobre o modelo de espalhamento de luz. Outras coisas, como ferramentas, um modelo de cidade, um modelo de iluminação e materiais, não são afetadas. Posso enviar os corajosos para ler a fonte ou assistir as gravações de como estou me afogando há horas - a maior parte do desenvolvimento foi em vídeo.

Uma história chata a perder

O trabalho nesse trabalho começou com a constatação de que o trabalho principal em tempo integral não deixa tempo para trabalhar em um trabalho completo de 4k - já é quase meados de março no pátio, faltam algumas semanas para o Revizen.
Resta apenas encontrar algo simples o suficiente para uma rápida, por algumas noites, enchimento de compo. Fazer outra marcha estúpida não é respeitar o espectador, então lembrei-me de que alguns anos atrás eu tinha que fazer um shader com espalhamento, e era bastante simples, compacto e ao mesmo tempo permitido, bonito, embora um tanto lento.

No decorrer de uma breve discussão, insisti por conta própria e decidimos nos concentrar no seguinte: criar uma paisagem cheia de luz difusa, com pôr do sol, nuvens e raios crepusculares (TIL como a expressão "raios divinos" é traduzida). Para não elevar o número de etapas na atmosfera a valores completamente não interativos, você precisa fazer um balanço forte (como o método do pátio de Monte Carlo), o que gera ruído visível. Mas não importa se você move a câmera e muda a cena lentamente e inicia a trilha ambiente, é possível misturar sem problemas os quadros adjacentes e suavizar temporariamente esse ruído.

Keen escreveu a música rapidamente - estava quase pronta duas semanas antes da revisão. No entanto, eu estava seriamente prejudicada pela gripe - com uma ambulância e uma doença infecciosa -, então praticamente não comecei a trabalhar no shader até o momento em que, numa condição de vida mais ou menos de alguma forma, peguei um avião para Frankfurt. O protótipo deste modelo de dispersão já estava escrito no ar.

Já tínhamos chicoteado a versão do intra da areia e da saliva na própria festa pelas poucas horas restantes antes do prazo (e, provavelmente, algumas depois; D), enquanto eu me afastava simultaneamente da gripe, falta de sono, voos de uma hora e ele estava constantemente distraído participando do compo de codificação ao vivo do Shader .

A versão mostrada na tela grande continha muitos artefatos e apenas a geometria rudimentar da cidade, com base no diagrama de Voronoi, com alturas aleatórias.

Em geral, o 12º lugar é bastante generoso.

A versão final, mostrada acima, foi feita mais tarde e em um modo mais descontraído, das 14h às 21h por semana, durante um mês. No total, foram necessárias entre 40 e 50 horas de trabalho.

Modelo de dispersão

(Observação: eu não faço programação gráfica profissionalmente. Esse é meu pequeno hobby aconchegante para o bem, se cem ou duas estiverem muito desfocadas sob cerveja horas de vinho por ano. Portanto, não há probabilidade zero de que algumas coisas sejam descritas abaixo e / ou nomeadas incorretamente. Tio, bata!)

O modelo de dispersão é emprestado do artigo "Espalhamento de luz externa de alto desempenho usando amostragem epipolar", de Egor Yusov , publicado no livro GPU Pro 5 , com amostragem epipolar completamente ejetada.

Modelo físico

Fótons solares bombardeiam a atmosfera da Terra e interagem com partículas de ar. Um fóton pode ser espalhado por uma partícula, o que implica uma mudança na direção do fóton, ou pode ser absorvido, o que significa que o fóton é perdido e sua energia foi convertida em alguma outra forma.
Ambos os processos são probabilísticos e dependem em particular da densidade de partículas e energia de fótons (que corresponde à sua cor).

Nos dedos, os fótons “vermelhos” têm uma chance menor de interagir com o ar, portanto superam a espessura da atmosfera relativamente intacta.
Os azuis, no entanto, têm uma maior probabilidade de dispersão, e é por isso que eles podem mudar de direção repetidamente e percorrer distâncias consideráveis ​​na atmosfera antes de alcançar (ou não) o observador.

Os parâmetros da interação da luz com o ar que nos interessam são os seguintes:

• $$$\ beta ^ s (x)$ - fração da luz dispersa por unidade de comprimento em um ponto $$$x$
• $$$\ beta ^ a (x)$ - fração da luz absorvida por unidade de comprimento em um ponto $$$x$
• $$$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$ - fração total de luz perdida por unidade de comprimento em um ponto $$$x$
• $$$p (\ alpha)$ É a distribuição angular da luz dispersa, onde $$$\ alpha$ este é o ângulo entre o incidente e o feixe disperso

Supõe-se que o ar consista em dois tipos de partículas, cuja dispersão ocorre independentemente: moléculas (modelo de Rayleigh) e aerossóis (partículas esféricas relativamente grandes, dispersão de Mie na literatura em inglês). Os modelos diferem apenas em valores diferentes para os parâmetros acima.

Para ambos os modelos, acredita-se que a densidade das partículas correspondentes diminua exponencialmente com a altura: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$ onde $$$\ rho_0$ - densidade ao nível do mar. Odds $$$\ beta$ proporcional $$$\ rho$ , e seus significados abaixo são dados para o nível do mar.

Rayleigh model

• $$$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$ [Nishita et al. 93, Preetham et ai. 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$ [Riley et al. 04, Bruneton e Neyret 08]
• $$$H_R = 7994m$ [Nishita et al. 93]

Aerossóis

• $$$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alfa)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$ [Nisita et al. 93, Riley et ai. 04] onde $$$g = 0,76$ [Bruneton e Neyret 08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$ [Bruneton e Neyret 08]
• $$$\ beta_M ^ e = 1,1 \ beta_M ^ s$
• $$$H_M = 1200 milhões$ [Nishita et al. 93]

Aproximação de espalhamento único

A aproximação da dispersão é baseada na emissão de um feixe de cada pixel da câmera e no cálculo de quanta luz da atmosfera deve receber dessa direção. Cada raio corresponde a todos os três componentes de luz RGB, como se três fótons com energias correspondentes voassem ao longo desse raio.

A luz que chega à câmara é formada pelos seguintes processos no ar:

• Dispersão (TIL que os figos aprendem a traduzir na dispersão). É adicionada a luz emitida pelo sol, que é probabilisticamente dispersa por um ângulo correspondente à direção da câmera.
• Absorção . A luz que já voa ao longo do feixe é absorvida pelo ar.
• Dispersão . A luz que já voa ao longo do feixe é perdida por se espalhar em outras direções.

Por motivos de desempenho, acreditamos que a luz só pode entrar na direção da câmera se espalhar uma vez, e todas as outras luzes (que foram espalhadas mais de uma vez) podem ser negligenciadas. Isso não é recomendado para o crepúsculo, mas o que fazer.

Essa abordagem é retratada na seguinte imagem bonita (eu tentei!):

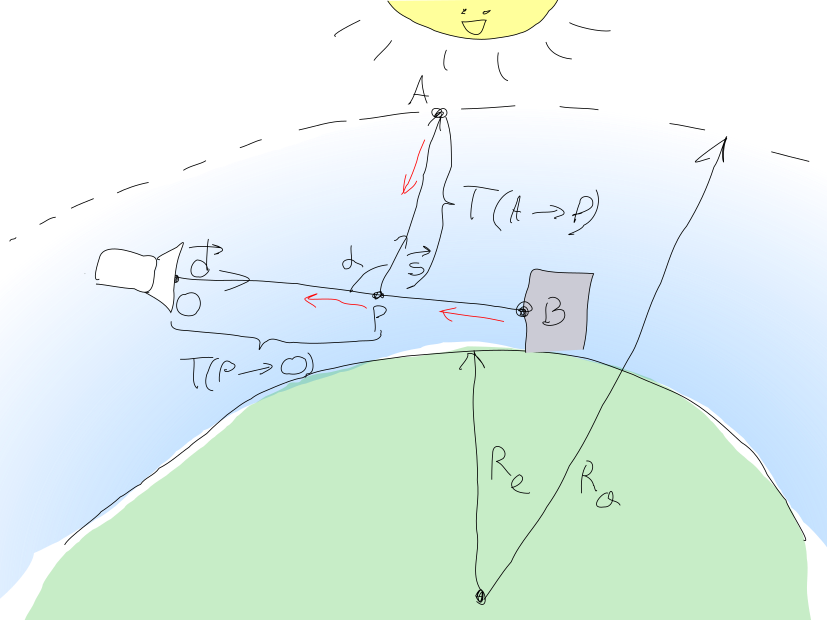
Assim, a quantidade de luz que deve ser detectada pelo pixel da câmera em $$$O$ pode ser calculado como a soma $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$ onde $$$\ mathbf {L_ {in}}$ - luz difusa do sol, e $$$\ mathbf {L_ {BO}}$ - a quantidade de luz do ponto $$$B$ cena geometria objeto atingindo $$$O$ .

Geometria da luz

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$ onde $$$\ mathbf {L_O}$ A luz emitida de um ponto $$$B$ em direção à câmera.

$$$\ mathbf {T} (B \ rightarrow O)$ chamada espessura óptica do meio entre os pontos $$$B$ e $$$O$ e é calculado da seguinte forma:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$$

Considerando que os membros $$$\ beta$ consistir na densidade constante e variável do nível do mar, esta expressão pode ser convertida em:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ barra {\ mathbf {\ beta}} \ cdot \ barra {T_ \ rho} (B \ rightarrow O)$$

Observe que eu não divulgo especificamente $$$\ rho$ , porque os alteraremos posteriormente ao adicionar nuvens. Também chamo a atenção para o fato de que $$$\ beta$ - vetores RGB (pelo menos $$$\ mathbf {\ beta_R}$ têm significados diferentes para os componentes RGB e $$$\ beta_M$ - vetor apenas por consistência). Membros com $$$\ rho$ sob a integral estão escalares.

Luz do sol

Luz do sol $$$\ mathbf {L_ {in}}$ calculado pela integração em todos os pontos $$$P$ ao longo do segmento $$$Ob$ e o acúmulo de toda a luz solar que entra na câmera e morre na espessura $$$\ mathbf {T} (P \ rightarrow O)$ .

A quantidade de luz solar atingindo um ponto $$$P$ é calculado por uma fórmula semelhante $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$ onde $$$\ mathbf {L_ {sun}}$ - o brilho do sol, e $$$A$ É o ponto em que o raio do ponto $$$P$ em direção ao sol $$$\ vec {s}$ sai da atmosfera. A fração dessa luz que será espalhada na direção da câmera é $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$ .

Total que obtemos:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ds$$

Você pode perceber que:

• $$$\ alpha$ é uma constante para cada raio de pixel da câmera (acreditamos que o sol está infinitamente distante e os raios dele são paralelos)
• Odds $$$\ beta$ consistem em constantes do nível do mar e funções de densidade $$$\ rho (s)$
• Funções $$$p (\ alpha)$ tem fatores comuns para ambos os processos de espalhamento

Isso permite converter a expressão em:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1 -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

onde

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$$I_m$ e $$$I_R$ diferem apenas nas funções de densidade; seus exponenciais são os mesmos.

Ninguém foi capaz de calcular essas integrais analiticamente, então elas precisam ser calculadas numericamente usando o re-mapeamento (como dizem nas publicações originais, você não pode fazê-lo!).

Integração numérica

Por razões de tamanho e preguiça, consideraremos o mais estúpido possível: $$$\ int_A ^ B f (x) dx \ approx \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {\ vec { B - A}} {N})$

A marcha dos raios será realizada na direção oposta ao fluxo de luz: do ponto da câmera $$$O$ antes da interseção da viga com geometria $$$B$ . Segmento de linha $$$O \ rightarrow B$ dividido por $$$N$ etapas.

Antes de iniciar a marcha, inicialize as variáveis:

• espessura óptica total acumulada vec2 (dois componentes separados, para espalhamento de Rayleigh e aerossol) $$$\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
• vec3 (RGB) $$$\ mathbf {I_M}$ , $$$\ mathbf {I_R}$

Avançar para o ponto $$$P_i$ cada passo entre $$$O$ e $$$B$ :

1. Vamos raio $$$\ vec {s}$ na direção do sol e conseguir um ponto $$$A_i$ a saída desse raio da atmosfera.
2. Calcular a espessura $$$\ mathbf {T} (A \ rightarrow P_i)$ calculando primeiro $$$\ int_A ^ {P_i} \ rho_M (s) ds$ e $$$\ int_A ^ {P_i} \ rho_R (s) ds$ usando a mesma nova marcação (com o número de etapas M ) e multiplique os termos resultantes pelas constantes correspondentes $$$\ beta_M ^ e$ e $$$\ mathbf {\ beta_R ^ e}$ .
3. Calcular a espessura $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. Acumular $$$\ mathbf {I_R}$ e $$$\ mathbf {I_M}$ usando esses valores

A cor final após o reimarching é calculada pela soma dos termos:

1. Prazo $$$\ mathbf {L_ {BO}}$ é trivial: uma variável que contém $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$ contém valor $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$ desde $$$P_i$ atingiu $$$B$ .
2. Por multiplicação $$$\ mathbf {I_R}$ e $$$\ mathbf {I_M}$ para as constantes correspondentes e adicionando o resultado é calculado $$$\ mathbf {L_ {in}}$

Shaders

Dispersão simples sem ninguém

Levemente penteado e comentado as fontes de dispersão extraídas (quase) diretamente do intra em si:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

Cale a boca no shader

As nuvens

Nada mal, mas essa imagem também pode ser obtida muito mais facilmente com uma pilha de gradientes astuciosa.

De uma maneira enganosa, obter nuvens e raios divinos é muito mais difícil. Vamos adicionar.

A idéia é aproximar as nuvens com aerossóis e modificar apenas a função densitiesRM() . Isso pode não ser tão fisicamente correto quanto gostaríamos (não tenho idéia de como a dispersão da luz nas nuvens na computação gráfica se aproxima).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

Ao contrário das expectativas, não temos nuvens bonitas, uma doce vitória e fãs, mas artefatos. Tentar aumentar o número de etapas dos artefatos na testa não remove completamente, mas prejudica significativamente o desempenho.

Soluções muletas que empurram o intra:

• Os artefatos mais desagradáveis ​​do horizonte estão escondidos atrás das montanhas
• As nuvens são adicionadas apenas perto da câmera.
• Monte-Karlovschina é adicionado, cada raio de marcha é deslocado por um deslocamento aleatório: for (float i = pixel_random.w; i < steps; ++i) . Isso aumenta o ruído que você precisa suavizar temporariamente misturando quadros sucessivos.

• O número de etapas para zonas que exigem mais detalhes está aumentando (por exemplo, uma camada com nuvens). É para isso que é feita uma separação tão absurda de funções em scatterImpl() e scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

Alinhamento com geometria da cena

Como resultado do mapeamento tradicional das funções de distância e sombra, a distância L ao ponto B e a cor do pixel Lo já foram obtidas. Esses valores são simplesmente substituídos na função scatter() . Se o feixe não descansar contra a geometria e sair da cena, a cor Lo zero e L calculada usando escape() - acredita-se que o feixe tenha deixado a atmosfera.

Como tudo.

... De fato, é claro, nem todos. É muito difícil esfregar todas as partes para que, como um todo, pareça crível. Apenas um monte de confusão com parâmetros distorcidos, geometria da cena, funções de ruído, trajetória e ângulo da câmera. Receio não ter bons conselhos aqui, exceto por repetir várias horas e bater a cabeça contra a parede.

Minificação

Depois de processar o minificador de sombreador , o código de dispersão final do sombreador tem aproximadamente 1500 bytes de tamanho. O Crinkler o compacta em ~ 700 bytes, o que representa cerca de 30% de todo o código de sombreador.

Reprodução

Eu não sei como computação gráfica.