Modelo de regressão polinomial

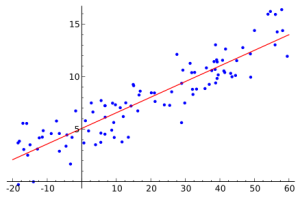
Em termos simples, o modelo de regressão em estatística matemática é construído com base em dados conhecidos, que são pares de números. O número de tais pares é predeterminado. Se você imagina que o primeiro número de um par é o valor da coordenada $$$x$ e o segundo $$$y$ , o conjunto desses pares de números pode ser representado no plano no sistema de coordenadas cartesianas como um conjunto de pontos. Esses pares de números não são tomados aleatoriamente. Na prática, como regra, o segundo número depende do primeiro. Construir uma regressão significa pegar uma linha (mais precisamente, uma função) que, o mais próximo possível, se aproxima (aproxima) de muitos dos pontos acima.

Para que serve tudo isso? Antes de tudo, isso é necessário para a preparação dos chamados previsões. Muitas vezes precisam descobrir $$$y$ sabendo apenas $$$x$ se for diferente do X, com base no qual a regressão foi construída. Vou dar um exemplo simples. Há estatísticas sobre a dependência do crescimento de uma pessoa em sua idade, com base em 100 pessoas diferentes estudadas. Assim, temos 100 pares de números {idade; crescimento}. Ao mesmo tempo, "crescimento" é uma quantidade dependente e "idade" é independente. Ao construir corretamente um modelo de regressão, podemos "prever" o crescimento com certeza por qualquer valor etário.

Na prática, dependendo da situação, linear, parabólico, poder e outros tipos de funções são usados ​​na construção de modelos de regressão. No curso da estatística matemática, o modelo de regressão linear é mais frequentemente considerado. Às vezes eles abordam um caso mais complicado - um modelo parabólico. Fazendo uma generalização, é fácil adivinhar que modelos lineares e parabólicos são casos particulares de um modelo mais complexo - polinomial. Construir um modelo de regressão significa encontrar os parâmetros da função que aparecerão nele. Para regressão linear - dois parâmetros: coeficiente e termo livre.

A regressão polinomial pode ser usada em estatísticas matemáticas para modelar os componentes de tendência de séries temporais. Uma série temporal é, de fato, uma série de números que dependem do tempo. Por exemplo, a temperatura média diária do ano passado ou a renda mensal da empresa. A ordem do polinômio simulado é avaliada por métodos especiais, por exemplo, pelo critério de série. O objetivo de construir um modelo de regressão polinomial no campo de séries temporais ainda é o mesmo - previsão.

Para começar, consideramos o problema da regressão polinomial de uma maneira geral. Todo raciocínio é baseado em uma generalização do raciocínio em problemas de regressão linear e parabólica. Após essas considerações, passarei a um caso especial - consideração desse modelo para séries temporais.

Sejam duas séries de observações $$$x_i$ (variável independente) e $$$y_i$ (variável dependente) $$$i = \ overline {1, n}$ . A equação polinomial tem a forma

$$

$$y = \ soma \ limites_ {j = 0} ^ k b_jx ^ j, \ \ \ \ \ (1)$$

onde $$$b_j$ - parâmetros deste polinômio, $$$j = \ overline {0, k}$ . Entre eles $$$b_0$ - um membro livre. Vamos encontrar os parâmetros dos mínimos quadrados (OLS) $$$b_j$ dada regressão.

Por analogia com a regressão linear, o OLS também se baseia em minimizar a seguinte expressão:

$$

$$S = \ soma \ limites_ {i = 1} ^ n \ esquerda (\ hat y_i-y_i \ right) ^ 2 \ to \ min \ \ \ \ \ \ (2)$$

Aqui $$$\ hat y_i$ - valores teóricos que são os valores do polinômio (1) nos pontos $$$x_i$ . Substituindo (1) em (2), obtemos

$$

$$S = \ soma \ limites_ {i = 1} ^ n \ esquerda (\ sum_ {j = 0} ^ kb_jx_i ^ j-y_i \ direita) ^ 2 \ a \ min.$$

Com base nas condições necessárias para o extremo da função $$$(k + 1)$ variáveis $$$S = S (b_0, b_1, \ pontos, b_k)$ equiparamos suas derivadas parciais a zero, ou seja,

$$

$$S '_ {b_p} = 2 \ sum \ limits_ {i = 1} ^ nx_i ^ p \ left (\ sum \ limits_ {j = 0} ^ kb_jx_i ^ j-y_i \ right) = 0, \ \ \ p = \ overline {0, k}.$$

Dividindo os lados esquerdo e direito de cada igualdade por 2, revelamos a segunda soma:

$$

$$\ sum \ limits_ {i = 1} ^ nx_i ^ p \ left (b_0 + b_1x_i + b_2x_i ^ 2 + \ dots + b_kx_i ^ k \ right) - \ sum \ limits_ {i = 1} ^ nx_i ^ py_i = 0 , \ \ \ p = \ overline {0, k}.$$

Abrindo os parênteses, transferimos em cada $$$p$ expressão, o último termo com $$$y_i$ para a direita e divida os dois lados por $$$n$ . Como resultado, conseguimos $$$(k + 1)$ expressões formando um sistema de equações normais lineares para $$$b_p$ . Tem a seguinte forma:

$$

$$\ left \ {\ begin {array} {l} b_0 + b_1 \ overline x + b_2 \ overline {x ^ 2} + \ dots + b_k \ overline {x ^ k} = \ overline y \\ b_0 \ overline x + b_1 \ overline {x ^ 2} + b_2 \ overline {x ^ 3} + \ dots + b_k \ overline {x ^ {k + 1}} = \ overline {xy} \\ b_0 \ overline {x ^ 2} + b_1 \ overline {x ^ 3} + b_2 \ overline {x ^ 4} + \ dots + b_k \ overline {x ^ {k + 2}} = \ overline {x ^ 2y} \\ \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \ ldots \\ b_0 \ overline {x ^ k} + b_1 \ overline {x ^ {k + 1}} + b_2 \ overline {x ^ {k + 2}} + \ dots + b_k \ overline {x ^ {2k}} = \ overline {x ^ ky} \ end {array} \ right. \ \ \ \ \ (3)$$

Você pode reescrever o sistema (3) na forma de matriz: $$$AB = C$ onde

$$

$$A = \ left (\ begin {array} {ccccc} 1 & \ overline x & \ overline {x ^ 2} & \ ldots & \ overline {x ^ k} \\ \ overline x & \ overline {x ^ 2 } & \ overline {x ^ 3} & \ ldots & \ overline {x ^ {k + 1}} \\ \ overline {x ^ 2} & \ overline {x ^ 3} & \ overline {x ^ 4} & \ ldots & \ overline {x ^ {k + 2}} \\ \ vdots e \ vdots e \ vdots e \ ddots e \ vdots \\ \ overline {x ^ k} e \ overline {x ^ {k + 1} } & \ overline {x ^ {k + 2}} & \ ldots & \ overline {x ^ {2k}} \ end {array} \ right), \ \ B = \ left (\ begin {array} {c} b_0 \\ b_1 \\ b_2 \\\ vdots \\ b_k \ end {array} \ right), \ \ C = \ left (\ begin {array} {c} \ overline y \\\ overline {xy} \\ \ overline {x ^ 2y} \\\ vdots \\\ overline {x ^ ky} \ end {array} \ right).$$

Agora nos voltamos para a aplicação dos fatos acima no caso de séries temporais. Que séries temporais sejam dadas $$$x_t$ onde $$$t = \ overline {1, n}$ . É necessário criar uma tendência de ordem polinomial $$$k$ , que aproxima a série temporal fornecida com a maior precisão possível. Como variável independente $$$x$ nós levaremos $$$t$ com base na definição de uma série temporal. Esses Xs são uma série de números naturais que indicam um período de tempo. Como $$$y$ valores de séries temporais são obtidos $$$x_t$ . Pode-se ver que os valores dos elementos $$$a_ {ij}$ matrizes do sistema $$$A$ independente de $$$x_t$ . Como no caso geral, obviamente,

$$

$$a_ {ij} = \ overline {x ^ {i + j-2}} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {i + j-2},$$

então no caso de séries temporais

$$

$$a_ {ij} = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {i + j-2},$$

onde $$$i, j = \ overline {1, (k + 1)}.$

Itens $$$c_j$ vetores matriciais de termos livres $$$C$ geralmente obtido como

$$

$$c_j = \ overline {x ^ {j-1} y} = \ frac1n \ sum \ limits_ {r = 1} ^ nx_r ^ {j-1} y_r.$$

E no caso de séries temporais

$$

$$c_j = \ frac1n \ sum \ limits_ {r = 1} ^ nr ^ {j-1} x_r,$$

onde $$$j = \ overline {1, (k + 1)}.$

Assim, tendo resolvido o sistema (3), podemos encontrar os parâmetros desejados da tendência polinomial $$$b_0, \ pontos, b_k.$

Para preencher as matrizes do sistema e resolvê-lo, um dos métodos numéricos pode ser usado ao modelar uma tendência em um computador. Nesse caso, o resultado do cálculo será bastante preciso.

Como resultado, o componente de tendência assumirá a forma:

$$

$$T_t = \ soma \ limites_ {i = 0} ^ kb_it ^ i, \ \ \ t = 0,1,2, \ pontos.$$

Também é importante notar que o componente de tendência simulado $$$T_t$ , determinado não apenas para os períodos atuais $$$[1; n]$ , mas também para períodos futuros $$$t> n$ .

Percebo imediatamente que a regressão polinomial modela apenas o componente de tendência da série temporal. Um modelo completo de série temporal também implica outros componentes, que estão além do escopo deste artigo.

Na prática, eu pessoalmente não vi séries temporais com uma ordem de tendência polinomial superior a 2. Isso explica a prevalência de modelos de regressão linear e prabólica como casos particulares de polinômio.