Se você descrever em algumas frases sobre qual princípio as trocas de classificação funcionam, então:

1. Elementos de matriz são comparados em pares
2. Se o elemento à esquerda ^{* for} maior que o elemento à direita, os elementos serão trocados
3. Repita as etapas 1 a 2 até a matriz ser classificada

^{* - o elemento à esquerda significa aquele do par comparado, mais próximo da borda esquerda da matriz. Consequentemente, o elemento à direita está mais próximo da borda direita.}

Peço desculpas imediatamente por repetir material conhecido. É improvável que pelo menos um dos algoritmos deste artigo seja uma revelação para você. Sobre essas classificações em Habré, ele já foi escrito várias vezes (inclusive eu - 1 , 2 , 3 ) e pergunta por que novamente para voltar a esse tópico? Mas desde que decidi escrever uma série coerente de artigos sobre todas as classificações no mundo , tenho que passar pelos métodos de troca, mesmo na versão expressa. Ao considerar as seguintes classes, já haverá muitos novos (e poucas pessoas sabem) algoritmos que merecem artigos interessantes separados.

Tradicionalmente, "trocadores" incluem classificações nas quais os elementos mudam (pseudo) aleatoriamente (bogosort, bozosort, permsort, etc.). No entanto, eu não os incluí nesta classe, pois eles não têm comparações. Haverá um artigo separado sobre essas classificações, onde filosofamos muito sobre a teoria das probabilidades, combinatória e morte térmica do Universo.

Tipo parvo :: Tipo Stooge

1. Compare (e, se necessário, altere) os elementos nas extremidades da sub-matriz.
2. Pegamos dois terços do subarray desde o início e aplicamos o algoritmo geral a esses 2/3 recursivamente.
3. Pegamos dois terços da sub-matriz do seu final e aplicamos o algoritmo geral a esses 2/3 recursivamente.
4. E, novamente, pegamos dois terços da sub-matriz desde o início e aplicamos o algoritmo geral a esses 2/3 recursivamente.

Inicialmente, uma sub-matriz é uma matriz inteira. E então a recursão divide o subarray pai em 2/3, faz comparações / trocas nas extremidades dos segmentos fragmentados e, eventualmente, organiza tudo.

def stooge_rec(data, i = 0, j = None): if j is None: j = len(data) - 1 if data[j] < data[i]: data[i], data[j] = data[j], data[i] if j - i > 1: t = (j - i + 1) // 3 stooge_rec(data, i, j - t) stooge_rec(data, i + t, j) stooge_rec(data, i, j - t) return data def stooge(data): return stooge_rec(data, 0, len(data) - 1) 

Parece esquizofrênico, mas, no entanto, é 100% correto.

Classificação lenta :: Classificação lenta

E aqui observamos o misticismo recursivo:

1. Se o subarray consistir em um elemento, concluiremos a recursão.
2. Se um subarray consistir em dois ou mais elementos, divida-o ao meio.
3. Aplicamos o algoritmo recursivamente à metade esquerda.
4. Aplicamos o algoritmo recursivamente à metade direita.
5. Os elementos nas extremidades da sub-matriz são comparados (e alterados, se necessário).
6. Aplicamos recursivamente o algoritmo a uma sub-matriz sem o último elemento.

Inicialmente, uma sub-matriz é a matriz inteira. E a recursão continuará diminuindo pela metade, comparando e alterando até classificar tudo.

 def slow_rec(data, i, j): if i >= j: return data m = (i + j) // 2 slow_rec(data, i, m) slow_rec(data, m + 1, j) if data[m] > data[j]: data[m], data[j] = data[j], data[m] slow_rec(data, i, j - 1) def slow(data): return slow_rec(data, 0, len(data) - 1) 

Parece bobagem, mas a matriz está ordenada.

Por que o StoogeSort e o SlowSort estão funcionando corretamente?

Um leitor curioso fará uma pergunta razoável: por que esses dois algoritmos funcionam? Eles parecem simples, mas não é muito óbvio que você possa classificar algo assim.

Vamos primeiro dar uma olhada na classificação lenta. O último ponto desse algoritmo sugere que os esforços recursivos da classificação lenta visam apenas colocar o maior elemento do subarray na posição mais à direita. Isso é especialmente perceptível se você aplicar o algoritmo a uma matriz com pedidos pendentes:



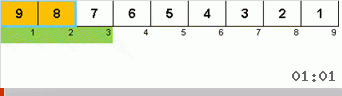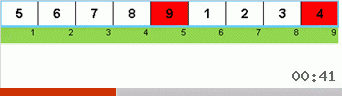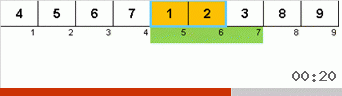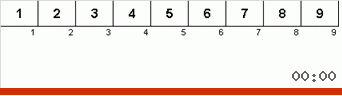
É claramente visto que em todos os níveis de recursão, os máximos migram rapidamente para a direita. Então esses máximos, onde estão onde são necessários, são desligados do jogo: o algoritmo se autodenomina - mas sem o último elemento.

No tipo Stooge, uma mágica semelhante acontece:



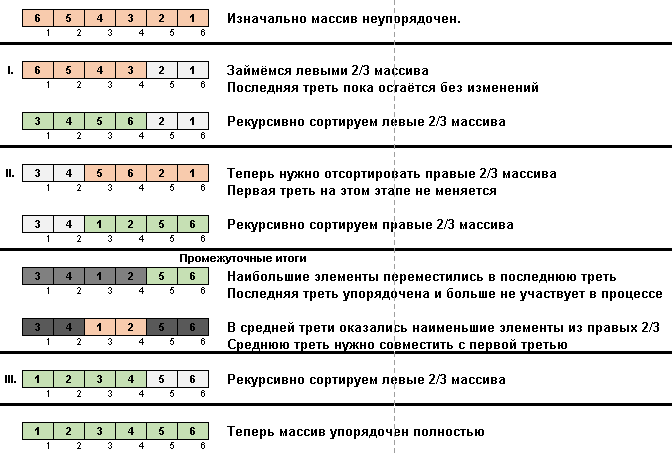
De fato, a ênfase também é colocada nos elementos máximos. Somente a classificação Lenta os move para o final, um por um, e a classificação Stooge empurra um terço dos elementos do sub-arranjo (o maior deles) empurra o terço mais à direita do espaço celular.

Nos voltamos para algoritmos, onde tudo já é bastante óbvio.

Classificação estúpida :: Classificação estúpida

Triagem muito cuidadosa. Vai do início da matriz até o fim e compara os elementos vizinhos. Se dois elementos vizinhos precisassem ser trocados, por precaução, a classificação retornará ao início da matriz e começará novamente.

 def stupid(data): i, size = 1, len(data) while i < size: if data[i - 1] > data[i]: data[i - 1], data[i] = data[i], data[i - 1] i = 1 else: i += 1 return data 

Classificação do Gnome :: Classificação do Gnome

Quase a mesma coisa, mas a classificação durante a troca não retorna ao início da matriz, mas leva apenas um passo para trás. Acontece que isso é suficiente para resolver tudo.

 def gnome(data): i, size = 1, len(data) while i < size: if data[i - 1] <= data[i]: i += 1 else: data[i - 1], data[i] = data[i], data[i - 1] if i > 1: i -= 1 return data 

Classificação otimizada de anões

Mas você pode economizar não apenas no recuo, mas também ao avançar. Com várias trocas consecutivas, você precisa dar o máximo de passos para trás. E então você precisa voltar (comparando ao longo do caminho os elementos que já estão ordenados em relação um ao outro). Se você se lembrar da posição em que as trocas começaram, poderá saltar imediatamente para essa posição quando as trocas forem concluídas.

 def gnome(data): i, j, size = 1, 2, len(data) while i < size: if data[i - 1] <= data[i]: i, j = j, j + 1 else: data[i - 1], data[i] = data[i], data[i - 1] i -= 1 if i == 0: i, j = j, j + 1 return data 

Classificação da bolha :: Classificação da bolha

Diferentemente da classificação estúpida e gnômica, ao trocar elementos na bolha, nenhum retorno ocorre - ele continua avançando. Chegando ao final, o maior elemento da matriz é movido para o final.

Em seguida, o processo de classificação repete todo o processo novamente, como resultado do qual o segundo elemento na antiguidade está em último lugar. Na próxima iteração, o terceiro maior elemento é o terceiro do final, etc.

 def bubble(data): changed = True while changed: changed = False for i in range(len(data) - 1): if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] changed = True return data 

Classificação de bolha otimizada

Você pode lucrar um pouco com os passes no início da matriz. No processo, os primeiros elementos são ordenados temporariamente um em relação ao outro (essa peça classificada muda constantemente de tamanho - diminui, aumenta). Isso é facilmente corrigido e, com uma nova iteração, você pode simplesmente pular um grupo desses elementos.
_{(Adicionarei a implementação testada no Python aqui um pouco mais tarde. Não tive tempo para prepará-la.)}

Classificação Shaker :: Classificação Shaker
(Tipo Cocktail :: Tipo Cocktail)

Uma espécie de bolha. Na primeira passagem, como de costume - empurre o máximo até o fim. Então damos uma volta brusca e empurramos o mínimo para o começo. As áreas marginais classificadas da matriz aumentam de tamanho após cada iteração.

 def shaker(data): up = range(len(data) - 1) while True: for indices in (up, reversed(up)): swapped = False for i in indices: if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] swapped = True if not swapped: return data 

Classificação ímpar-par :: Classificação ímpar-par

Mais uma vez, iterações sobre comparação pareada de elementos vizinhos ao mover da esquerda para a direita. Primeiro, compare os pares nos quais o primeiro elemento é ímpar na contagem e o segundo é par (ou seja, o primeiro e o segundo, o terceiro e o quarto, o quinto e o sexto, etc.). E então vice-versa - par + ímpar (segundo e terceiro, quarto e quinto, sexto e sétimo, etc.). Nesse caso, muitos elementos grandes da matriz em uma iteração ao mesmo tempo dão um passo à frente (na bolha, o maior da iteração chega ao fim, mas o restante dos quase grandes quase permanece no lugar).

A propósito, este era originalmente um tipo paralelo com O (n) complexidade. Será necessário implementar o AlgoLab na seção "Classificação paralela".

 def odd_even(data): n = len(data) isSorted = 0 while isSorted == 0: isSorted = 1 temp = 0 for i in range(1, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 for i in range(0, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 return data 

Classificação do pente :: Classificação do pente

A modificação mais bem sucedida da bolha. O algoritmo de velocidade compete com a classificação rápida.

Em todas as variações anteriores, comparamos os vizinhos. E aqui, primeiro, são considerados pares de elementos que estão a uma distância máxima um do outro. A cada nova iteração, essa distância diminui uniformemente.

 def comb(data): gap = len(data) swaps = True while gap > 1 or swaps: gap = max(1, int(gap / 1.25)) # minimum gap is 1 swaps = False for i in range(len(data) - gap): j = i + gap if data[i] > data[j]: data[i], data[j] = data[j], data[i] swaps = True return data 

Classificação rápida :: Classificação rápida

Bem, o algoritmo de troca mais avançado.

1. Divida a matriz ao meio. O elemento do meio é a referência.
2. Passamos da borda esquerda da matriz para a direita, até encontrarmos um elemento que é maior que o de referência.
3. Passamos da borda direita da matriz para a esquerda até encontrarmos um elemento menor que o de referência.
4. Trocamos os dois elementos encontrados nos pontos 2 e 3.
5. Continuamos a executar os itens 2-3-4 até que uma reunião ocorra como resultado do movimento mútuo.
6. No ponto de encontro, a matriz é dividida em duas partes. Para cada parte, aplicamos recursivamente um algoritmo de classificação rápida.

Por que isso funciona? À esquerda do ponto de encontro, existem elementos menores ou iguais ao ponto de referência. À direita do ponto de encontro, existem elementos maiores ou iguais à referência. Ou seja, qualquer elemento do lado esquerdo é menor ou igual a qualquer elemento do lado direito. Portanto, no ponto de encontro, a matriz pode ser dividida com segurança em dois subarrays e classificar cada subarray de maneira semelhante recursivamente.

 def quick(data): less = [] pivotList = [] more = [] if len(data) <= 1: return data else: pivot = data[0] for i in data: if i < pivot: less.append(i) elif i > pivot: more.append(i) else: pivotList.append(i) less = quick(less) more = quick(more) return less + pivotList + more 

K-sort :: K-sort

Em Habré, é publicada uma tradução de um dos artigos, que relata a modificação do QuickSort, que supera a classificação piramidal em 7 milhões de elementos. A propósito, isso por si só é uma conquista duvidosa, porque a classificação piramidal clássica não quebra os recordes de desempenho. Em particular, sua complexidade assintótica sob nenhuma circunstância atinge O (n) (uma característica deste algoritmo).

Mas a coisa é diferente. De acordo com o pseudocódigo do autor (e obviamente incorreto), geralmente não é possível entender qual é, de fato, a principal idéia do algoritmo. Pessoalmente, tive a impressão de que os autores são alguns criminosos que agiram de acordo com este método:

1. Declaramos a invenção de um algoritmo de super-classificação.
2. Reforçamos a declaração com um pseudo-código não funcional e incompreensível (como inteligente e claro, mas os tolos ainda não conseguem entender).
3. Apresentamos gráficos e tabelas que supostamente demonstram a velocidade prática do algoritmo em big data. Devido à falta de um código realmente funcional, ninguém ainda poderá verificar ou refutar esses cálculos estatísticos.
4. Publicamos bobagens em Arxiv.org sob o disfarce de um artigo científico.
5. LUCRO !!!

Talvez eu esteja falando em vão para as pessoas e, de fato, o algoritmo está funcionando? Alguém pode explicar como o k-sort funciona?

UPD Minhas acusações completas de classificar autores de fraude acabaram sendo infundadas :) O usuário jetsys descobriu o pseudo-código do algoritmo, escreveu uma versão de trabalho em PHP e me enviou em mensagens privadas:

Anúncio

Era tudo uma teoria, é hora de começar a praticar. O próximo artigo está testando trocas de classificação em diferentes conjuntos de dados. Vamos descobrir:

• Que classificação é a pior - boba, sem graça ou sem graça?
• Otimizações e modificações na classificação de bolhas realmente ajudam?
• Sob quais condições os algoritmos lentos são facilmente rápidos na velocidade do QuickSort?

E quando descobrimos as respostas para essas perguntas mais importantes, podemos começar a estudar as próximas aulas - tipos de inserção.

Referências

Aplicativo AlgoLab do Excel , com o qual você pode visualizar passo a passo a visualização desses tipos (e não apenas deles).

Wiki - Parvo / Pateta , Lento , Anão / Gnomo , Bolha / Bolha , Agitador / Agitador , Ímpar / Par , Pente / Pente , Rápido / Rápido

Artigos da série

• Aplicativo Excel AlgoLab.xlsm
• Classificações de Câmbio
  • Comparação de Classificação do Exchange
• Classificações de inserção
• Classificar por seleção
• Mesclar classificações
• Classificar por distribuição
• Classificação híbrida