Richard Hamming: Capítulo 17. Filtros Digitais - IV

"O objetivo deste curso é prepará-lo para o seu futuro técnico."

Oi Habr. Lembre-se do impressionante artigo “Você e seu trabalho” (+219, 2442 favoritos, 393k leituras)?

Portanto, Hamming (sim, sim, códigos de Hamming com auto-verificação e auto-correção) tem um livro inteiro escrito com base em suas palestras. Estamos traduzindo, porque o homem está falando de negócios.

Este livro não é apenas sobre TI, é um livro sobre o estilo de pensamento de pessoas incrivelmente legais. “Isso não é apenas uma carga de pensamento positivo; descreve condições que aumentam as chances de fazer um ótimo trabalho. ”

Já traduzimos 24 (de 30) capítulos. E estamos trabalhando em uma edição em papel.

Capítulo 17. Filtros Digitais - IV

(Obrigado pela tradução, Andrei Pakhomov, que respondeu à minha ligação no "capítulo anterior".) Quem quiser ajudar com a tradução, o layout e a publicação do livro - escreva em um e-mail pessoal ou magisterludi2016@yandex.ru

E agora nos voltamos para filtros recursivos, que têm a seguinte forma:



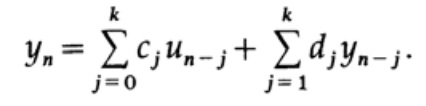
Essa fórmula mostra que só temos valores em um lado do enésimo valor atual. Usamos os valores anteriores do sinal e seu valor no momento atual un, bem como os valores anteriores obtidos na saída do filtro.
Essa abordagem clássica é o resultado do fato de que geralmente processamos o sinal em tempo real e não temos acesso a valores futuros do sinal.

Lembrando o básico, veremos que, se tivéssemos "valores futuros", provavelmente a previsão bidirecional seria muito mais precisa. Então, para calcular yn, encontraríamos um sistema que resolveria instantaneamente equações lineares - tudo bem na era da computação barata. Deixaremos essa observação de lado, hoje gravamos frequentemente o sinal em fita ou em outra mídia e depois processamos os dados em laboratório - e, portanto, temos valores futuros para algum ponto no tempo. Por exemplo, o uso de um filtro digital recursivo no processamento de imagens seria tolo, pois não usa algumas das informações relevantes disponíveis.

O próximo aspecto no qual você precisa prestar atenção ao usar o valor de saída anterior, como a próxima entrada, é a presença de feedback - e isso automaticamente levanta a questão da estabilidade. Essa é uma condição que devemos monitorar constantemente durante o projeto de filtros recursivos. Isso limita o que podemos fazer. Nesse caso, estabilidade significa que o efeito das condições iniciais não começará a prevalecer no resultado final.

Ao trabalhar com um sistema linear, vimos que, independentemente da frequência que aplicamos à entrada do filtro quando está estacionária, apenas essa frequência aparece na saída do filtro, embora a fase do sinal de saída possa ser alterada em relação à fase do sinal original. No entanto, no estado de transição, podem aparecer outras frequências que surgem da solução de uma equação diferencial homogênea. Um filtro recursivo nada mais é do que uma solução de uma equação diferencial com coeficientes constantes para termos un que formam uma função forçante.

Portanto, para um estado estacionário (ignorando transientes), assumimos que



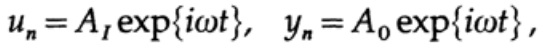
(onde A pode ser números complexos para levar em consideração a mudança de fase), e isso leva à solução da razão A0 / A1 para encontrar a função de transferência:



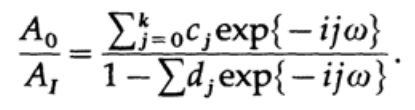
Essa expressão é uma função racional da variável complexa exp {iωt} = z, em contraste com o filtro não recursivo anteriormente considerado, onde a característica de transferência era um polinômio em z. A parte teórica da representação da função na forma de expansão em uma série de Fourier é desenvolvida; mas até agora não há teoria sobre a representação de funções como as relações de duas séries de Fourier (acho que não há razões para que tal teoria não exista). Portanto, no momento, os métodos de design não são sistemáticos (o que Kaiser fez para o design de filtros não recursivos), mas são um conjunto de truques.

Assim, temos um filtro Butterworth, dois tipos de filtros Chebyshev (dependendo da presença da mesma ondulação nas faixas de passagem e supressão) e um filtro elíptico (que é assim chamado devido ao uso de funções elípticas), que tem a mesma ondulação nas duas bandas.



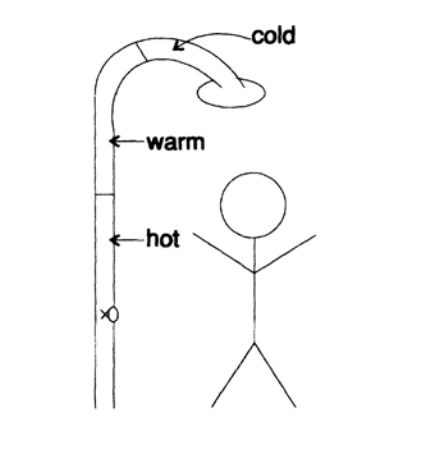Figura 17.1

Vou tocar apenas no tópico de feedback. Para esclarecer o problema de feedback, contarei uma história sobre mim. Era uma vez, participei de uma série de seis programas de televisão de meia hora em computadores e computação. As filmagens ocorreram principalmente em San Francisco. Eu costumava ficar lá e tinha o hábito de ficar no mesmo quarto no mesmo hotel - é ótimo conhecer o quarto com todos os detalhes quando já é tarde da noite e você está cansado ou quando precisa acordar no meio da noite - daí o desejo de ficar no mesmo o quarto.

É ótimo que o encanador conecte o chuveiro a tubos grandes (Figura 17.I). Como resultado, de manhã, quando comecei a tomar banho, a água estava muito fria, girei a torneira com água morna mais, ainda muito fria e mais, ainda muito fria e ainda mais e, finalmente, quando a água atingiu a temperatura certa Eu fiquei. É claro que a água ficava cada vez mais quente quando a água que entrava nos canos saía, e eu tive que pular do chuveiro e tentar novamente encontrar uma posição adequada para o manuseio da torneira da água quente. O atraso no fornecimento de água quente me causou transtornos. Apesar da rica experiência, me encontrei em uma situação clássica de instabilidade. Você pode observar essa situação de um dos dois lados: minha resposta foi muito forte (fui muito rude em minhas ações) ou a detecção do sinal foi muito tarde (fui muito apressado em ajustar a torneira). O mesmo efeito duradouro! Eu nunca tive que lidar com longos atrasos antes, então todos os dias minha manhã começava com inconvenientes! Neste exemplo ilustrativo, você pode olhar para a própria essência da instabilidade.

Aqui não vou me aprofundar no projeto de filtros recursivos, apenas observo que durante a luta com fórmulas corretivas para a solução numérica de equações diferenciais ordinárias, desenvolvi independentemente uma teoria.

O corretor no método preditor-corretor tem a forma



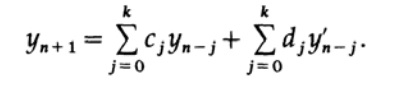
Vemos que agora os coeficientes uj do filtro recursivo são as derivadas yn 'da saída do filtro, extraídas da equação diferencial. Os filtros não recursivos convencionais não têm um loop de feedback - os valores calculados de yn não aparecem posteriormente no lado direito da expressão. Nas equações diferenciais, elas aparecem no loop de feedback e em suas derivadas, formando outro loop de feedback, geralmente não linear. Portanto, a estabilidade no campo de solução de equações diferenciais é um tópico mais complicado do que no campo de filtros recursivos.

Esses filtros recursivos são freqüentemente chamados de "filtros com resposta de impulso infinito" (filtros IIR), porque uma única perturbação será ecoada pelo loop de feedback, que decairá exponencialmente e somente se o filtro estiver estável. Eu não seria eu mesmo se não me perguntasse se todos os filtros recursivos deveriam ter essa propriedade. Logo encontrei o exemplo oposto. Na verdade, esse não é o tipo de filtro que você normalmente cria, mas este exemplo mostra que essa afirmação é superficial. Se você se perguntar se tudo o que diz é verdade, ficará surpreso com quantas coisas são falsas, mesmo em áreas bem projetadas!

No capítulo 26, abordarei a questão de trabalhar com especialistas. Agora você verá um exemplo do que acontece com muita frequência. Os especialistas foram informados sobre algo na sala de aula quando ainda eram estudantes, e não fizeram perguntas, simplesmente consideraram isso um fato. E eles constantemente reproduzem esse fato aceito, sem sequer tentar verificar se é verdade ou não, especialmente em relação ao problema que eles estão tentando resolver neste momento.

Deixe-me contar outra história agora. Uma senhora do departamento de matemática do Laboratories Labs Bella estava dançando uma dança quadrada com um dos físicos em uma festa de fim de semana e, na segunda-feira de manhã, no corredor, ela me mencionou um problema que ele estava tendo. Ele mediu o número de pulsos em um experimento radioativo em cada um dos, se bem me lembro, 256 níveis de energia. Isso é chamado de espectro do processo. O problema dele era obter uma derivada dos dados.

Portanto, você sabe que (a) o número de pulsos de um determinado nível de energia formará uma curva com descontinuidades e (b) diferenciá-lo para obter um coeficiente angular local não é uma tarefa fácil por si só. Quanto mais eu pensava na nota aleatória dela, mais eu sentia que ele precisava de um bom ajudante - ou seja, eu! Encontrei-o na lista telefônica dos Laboratórios Bell e expliquei a ele meu interesse e como cheguei a ele. Ele imediatamente quis ir ao meu escritório, mas eu era teimosa e insisti em me encontrar em seu laboratório. Ele tentou oferecer seu escritório, mas eu ainda insisti em seu laboratório. Porque A fim de avaliar suas habilidades e decidir se o problema dele vale meu tempo e esforços, pois prometeu ser um osso duro de roer. Ele passou no teste com brilhantismo pelo laboratório - ficou claro que ele era um experimentador muito competente.

Ele estava quase no limite do que podia fazer - os dados foram coletados por uma semana e a fonte de radiação foi ocultada por muitas telas. Não parecia que você poderia fazer mais nada para coletar dados mais precisos. Além disso, logo fiquei convencido, apesar de conhecer poucos detalhes, que seu experimento era importante para a física e também para os Laboratórios Bell. Então, eu assumi essa tarefa. Moral: até certo ponto, você pode escolher e trabalhar nas tarefas que considera importantes.

Obviamente, esse era um problema de suavização, e a Kaiser, de fato, apenas me treinou, então o que poderia ser melhor do que trazer o pesquisador para a Kaiser e pedir à Kaiser para projetar um filtro diferenciador adequado? Os problemas começaram imediatamente. Kaiser sempre pensou no sinal como uma função do tempo, e na área sob a curva como energia, e neste caso a energia era uma variável independente! Nesse ponto, o problema com Kaiser foi repetido até que eu lhe disse diretamente: "Bem, sua energia é tempo, e suas medidas, impulsos, essa voltagem". Somente depois disso a Kaiser conseguiu resolver o problema.

A maldição dos especialistas reside na compreensão limitada do que eles podem fazer. Mencionei a você que Kaiser é uma pessoa muito capaz, mas sua experiência, como costuma acontecer com especialistas, limitou sua visão. Você pode, por sua vez, fazer melhor? Espero que essas histórias o ajudem a evitar essa armadilha.

Como observei anteriormente, geralmente o espectro do sinal útil está na parte inferior da banda Nyquist, e o espectro de ruído é distribuído por toda a banda Nyquist; portanto, tivemos que encontrar a frequência de corte entre o sinal útil do físico e o ruído branco achatado. Como encontrá-la? No começo, tentei um modelo teórico do experimento com a cabeça do físico que estava na cabeça dele - havia muitas linhas espectrais estreitas na forma de funções gaussianas sobre uma ampla função gaussiana (duvidei que essa fosse uma distribuição de Cauchy, mas não discuti com ela, pois a diferença seria muito pequeno, dada a natureza dos dados que tínhamos). Assim, simulamos essa distribuição e ele preparou uma certa quantidade de dados sintéticos correspondentes a esse modelo. Uma análise espectral rápida do sinal através da transformação rápida de Fourier mostrou que o sinal está localizado no 1/20 inferior da banda de Nyquist. Além disso, processamos seus dados experimentais da mesma maneira e obtivemos o mesmo local de frequência de corte! Que sorte! (Talvez a sorte deva ser atribuída à habilidade do experimentador). Era uma vez teoria e prática reunidas! Descobrimos que fomos capazes de filtrar 95% do ruído. Finalmente, Kaiser escreveu um programa para ele que sintetizou um filtro para uma determinada frequência de corte, que foi definida pelo pesquisador.

O programa (1) calculou um filtro diferenciador adequado, (2) escreveu um programa para calcular a saída suavizada e, em seguida (3) processou os dados com este filtro sem nenhuma intervenção do físico.

Mais tarde, peguei um físico ajustando a frequência de corte para diferentes partes dos dados de nível de energia obtidos em uma série de medições e fui forçado a lembrá-lo de que existem certos "graus de liberdade" e o que ele faz não é um processamento honesto de dados. Tornou-se muito mais problemático quando as coisas estavam indo bem, convencê-lo a tirar o máximo proveito de seus dados (o que era muito caro de obter) - ele deveria trabalhar com as raízes quadradas de seus impulsos, pois eles tinham a mesma variação. Finalmente, ele entendeu isso e o fez. Ele e Kaiser escreveram um trabalho clássico nessa área que abriu as portas para coisas novas que poderiam ser feitas.

Minha contribuição Principalmente, primeiro identifique o problema, depois junte as pessoas certas e observe Kaiser para confrontá-lo com o fato de que a filtragem é necessária não apenas para sinais como funções do tempo e, finalmente, lembre-os do que sabiam das estatísticas (ou deveriam ter). saber, mas talvez eles não soubessem).

Com base no meu, parece-me que a necessidade de tal papel aumenta à medida que as pessoas se tornam cada vez mais especialistas em áreas de conhecimento cada vez mais estreitas. Alguém precisa manter amplos horizontes e garantir que as coisas sejam feitas com honestidade. Acho que cheguei a esse cargo depois de uma educação muito longa, sob a liderança de John Tukey, além de uma boa base na forma de uma ferramenta universal da ciência chamada Matemática. Vou falar sobre a natureza da matemática no capítulo 23 .

A maior parte do processamento do sinal vem de sinais ao longo do tempo. Ao mesmo tempo, a maioria dos filtros digitais é projetada para estudos pequenos e altamente especializados que não estão necessariamente associados a sinais ao longo do tempo. Aqui vou pedir para você tomar cuidado no futuro. Suponha que você administre os negócios no topo e esteja interessado nos dados que mostram os custos de mão-de-obra anteriores dos equipamentos. Serão dados ruidosos, mas você ainda deseja entender, no sentido usual, o que acontece na organização - que processos de longo prazo estão ocorrendo - aqueles que são tão lentos que as pessoas os compreendem quando já acontecem, mas mesmo assim entendem captura que é de fundamental importância se você quer ser um bom gerente. Você precisará de um filtro digital para suavizar os dados e ver dicas da tendência, se houver. Você não deseja encontrar uma tendência que não existe, mas, se ela existe, realmente quer saber o que era antes para prever o que é provável que seja no futuro próximo. De fato, você desejará ver mudanças na inclinação da tendência, se os dados permitirem vê-la. Alguns sinais, como poder de fogo em relação ao deslocamento do navio, não estão vinculados ao tempo, mas podem dizer muito sobre o estado atual da frota. Obviamente, você pode estudar essa relação em função do tempo.

No topo de sua carreira, você poderá usar uma variedade de filtros digitais de baixo nível para sinais em função do tempo, e não apenas para gerenciar melhor as coisas. Portanto, argumento que você provavelmente sintetiza muito mais filtros digitais para coisas fora do padrão do que para reduzir o tamanho dos dados de radar e aplicativos clássicos semelhantes. Geralmente é em novas aplicações de conhecimento que você pode obter o máximo retorno.

Permitam-me expressar algumas preocupações com relação ao uso incorreto de ferramentas inteligentes; em mais detalhes falarei sobre tópicos próximos às estatísticas no Capítulo 27 . A análise de expansão de Fourier assume a linearidade do modelo subjacente. Você pode usá-lo para casos levemente não lineares, mas mais frequentemente do que não, a análise feita com habilidade pela expansão de Fourier falha, pois o fenômeno investigado é de natureza não linear demais. Vi como milhões de dólares foram desperdiçados quando era bastante óbvio para quem estava de fora que as não linearidades distorceriam toda a análise linear feita por aproximação pelas séries de Fourier. Quando eles apontaram isso, a resposta foi que eles não sabiam que outra abordagem poderia ser adotada e continuaram fazendo a coisa errada! E não estou exagerando aqui.



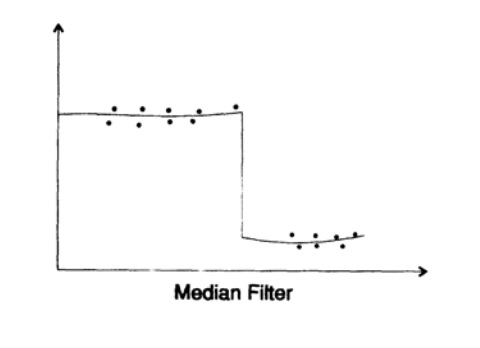Figura 17.2

E os filtros não lineares? As possibilidades aqui são infinitas e dependem, é claro, do problema com o qual você está lidando. Vou lidar com apenas um deles, o filtro mediano.Você considera a saída mediana do filtro para um conjunto de dados específico. Vamos ver como isso funciona na prática. Antes de tudo, observamos que ele busca suavizar qualquer ruído local, mas como o filtro se comportará no ponto de interrupção (Fig. 17.2)?

Com um número ímpar de membros no filtro mediano, você verá que a saída do filtro permanece no nível superior até mais da metade dos pontos na entrada do filtro estar no nível inferior, após o qual a saída do filtro "salta" para baixo. Ele seguirá bem os intervalos e não tentará suavizá-los completamente! Em alguns casos, esse é exatamente o tipo de filtro mais adequado para você - o ruído local é suavizado, enquanto mudanças repentinas no estado do sistema em estudo não serão perdidas.

Repito que a análise da série de Fourier é linear, enquanto há um grande número de filtros não lineares, mas a teoria não está bem desenvolvida para outra coisa senão um filtro mediano. O filtro Kalman é outro exemplo do uso de um filtro parcialmente não linear, a parte não linear é o “ajuste” independente do filtro ao sinal.

Finalmente, aqui está outra observação fundamental que fiz ao estudar filtros digitais. Um dia, enquanto estudava um livro sobre integrais de Fourier, encontrei um teorema que afirmava que a variação de uma função multiplicada pela variação de sua transformação deveria ser maior que uma determinada constante. Eu me perguntei: “O que é isso senão o famoso princípio da incerteza da Mecânica Quântica”? Sim, toda teoria linear deve ter um princípio de incerteza que vincule variáveis ​​conjugadas. Assim que você adota a abordagem linear, e o CM afirma a aditividade absoluta dos eigenstates, você deve descobrir o princípio da incerteza. A invariância linear do tempo leva automaticamente às funções próprias e ^ iω (t). Eles imediatamente levam à série de Fourier e, por sua vez, têm o princípio da incerteza.É como se você estivesse usando óculos azuis. Tudo o que você olha, deve ter um tom azulado!

Portanto, você não tem certeza se o famoso princípio da incerteza de CM existe ou não; talvez esse seja apenas o efeito da linearidade implícita do sistema.

Poucas pessoas querem acreditar que o que vemos depende de que lado abordamos o problema! Muitas vezes vemos o que queremos ver, e é por isso que você deve usar uma abordagem científica em qualquer lugar, duvidando de suas próprias crenças.
Para demonstrar isso claramente, repetirei a história de Eddington sobre pescadores. Pescaram na rede e, quando examinaram o tamanho dos peixes capturados na rede, decidiram que havia um tamanho mínimo de peixe no mar.

Concluindo, se você não duvida das regras adotadas, de vez em quando, provavelmente não se tornará líder em nenhum campo; por outro lado, se duvidar de tudo, ficará paralisado e não fará nada. . Quando duvidar, quando aprender o básico, quando pensar por si mesmo e quando continuar e aceitar as coisas como são, isso é uma questão de estilo de pensamento, e não posso dar uma fórmula simples para resolver esse problema. Você deve aprender com sua própria experiência. Grandes ganhos geralmente ocorrem após mudanças significativas nas premissas subjacentes nas quais a área se baseia. O estado de nosso conhecimento determina o equilíbrio entre vários aspectos da pesquisa. Parece que quando você é jovem, a intuição e a percepção têm mais tempo para dar resultado, mas quando você é velho,resta menos tempo para isso e provavelmente deve se concentrar no que já está ao seu alcance.

Para continuar ...

Quem quer ajudar na tradução, layout e publicação do livro - escreva em um e-mail pessoal ou envie um e-mail para magisterludi2016@yandex.ru

A propósito, também lançamos a tradução de outro livro interessante - “A Máquina dos Sonhos: a História da Revolução Computacional” )