Informações sobre o estado do ambiente ou, por exemplo, um determinado objeto de controle podem ser obtidas medindo os valores atuais dos parâmetros que caracterizam certas propriedades do ambiente ou objeto. Para receber, processar e transmitir essas informações por meios técnicos, o valor do parâmetro medido deve ser convertido por dispositivos de medição automáticos em um sinal de informações de medição. Para fazer isso, implemente o canal de medição de informações (
CII ), como uma combinação de meios técnicos, cada um dos quais cumprirá sua função específica, começando na percepção do valor medido e terminando com o recebimento das informações de medição de uma forma conveniente para a percepção humana ou para seu processamento posterior. E tudo ficaria bem, mas ao longo do caminho da informação, a interferência
e (t) é sobreposta ao sinal útil
y (t) da informação de medição - uma função aleatória do tempo que pode simular o erro aleatório do transdutor de medição, captadores elétricos nos fios de conexão e ondulações aleatórias parâmetro medido e outros fatores.
Com base nisso, surge o problema do processamento primário de informações na CII - filtrando o sinal y (t) das informações de medição da interferência aleatória e (t). Basicamente, os métodos de filtragem são baseados na diferença nos espectros de frequência das funções y (t) ee (t), e a interferência é considerada mais alta frequência.
A síntese do filtro ideal implementado é uma tarefa complexa, cuja solução requer a especificação exata das características do sinal e da interferência úteis. Portanto, na prática, a função de transferência do filtro é geralmente especificada e limitada à síntese paramétrica usando algoritmos de filtragem simples.
Os métodos de filtragem são realizados no nível do software e no nível do hardware. Por exemplo, no sensor BMP280 (BOSCH), é possível conectar um filtro IIR no nível do hardware, alterando o coeficiente do filtro k, se necessário, [1].
Filtro IIR
Os filtros com resposta de impulso infinito são filtros recursivos e calculam o sinal de saída com base nos valores das amostras anteriores de entrada e saída. Teoricamente, a resposta de impulso de um filtro IIR nunca chega a zero; portanto, a saída é infinita em duração.
Em geral, escrevemos o algoritmo para filtrar um filtro digital escalar unidimensional como [2]:
(1)
onde
T é uma função escalar de uma variável.
A função
T depende do sinal de entrada atual x [n] e anterior: M amostras do sinal de entrada
e N amostras do sinal de saída
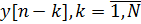
A saída do filtro IIR é descrita por uma equação de diferença da forma:
2)
onde x [n], y [n] é a entrada e a saída do filtro, respectivamente, {
} É o conjunto de coeficientes diretos, M é o número de coeficientes diretos, {
} É um conjunto de coeficientes inversos, N é o número de coeficientes inversos.
Aplicando a transformação z em ambos os lados da equação (2), obtemos:
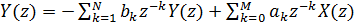
(3)
Em seguida, a função de transferência do filtro ficará assim:
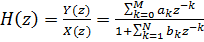
4)
Algoritmo para filtrar um filtro IIR unidimensional
Em termos gerais, o algoritmo de filtragem para um filtro recursivo estacionário escalar unidimensional se parece com:
. (5)
Agora, escrevemos a equação da diferença para o filtro IIR no formato [1]:
(6)
onde k é o coeficiente de filtro;
ou
(7)
onde
São os coeficientes de filtro inverso e direto, respectivamente.
A partir de (7), é óbvio que em k = 1 o sinal de saída do filtro repetirá a entrada e, à medida que o coeficiente de filtro k aumenta, o peso do sinal filtrado anterior tende a 1 e o peso do valor medido tende a 0.
O algoritmo (6) é implementado como um exemplo do canal de medição de informações de pressão atmosférica absoluta para o sensor BMP280, no nível do software no ambiente de desenvolvimento do Software Arduino (IDE), lista 1. O diagrama de conexão elétrica dos componentes da CII é mostrado na Fig. 1. A vista geral do protótipo da pressão atmosférica absoluta da CII é apresentada na Fig. 2. O protótipo fornece a capacidade de alterar o coeficiente do filtro na faixa de 1 a 50 em incrementos de 1, girando o botão do potenciômetro. O sinal do visor de cristal líquido mostra o valor da pressão medida (para k = 1) ou o valor filtrado (para k = 2 ... 50) e o coeficiente do filtro k.
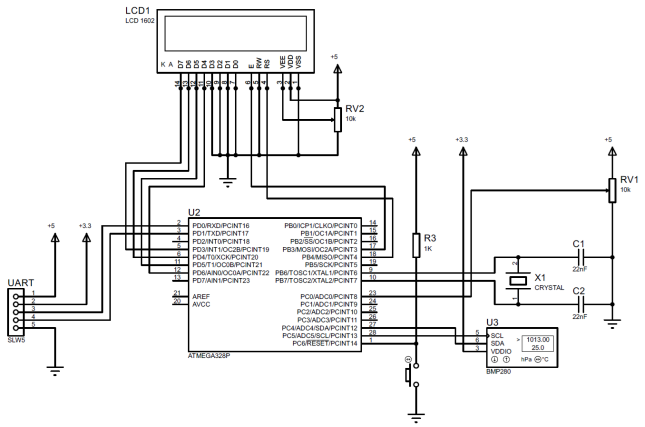Fig. 1 - Diagrama de fiação dos componentes do protótipo CII
Fig. 2 - Visão geral do protótipo CIIScript Python para pesquisar filtros IIR
A Listagem 2 mostra um script Python para examinar os filtros IIR. O coeficiente de filtro k está escrito no script. Os valores de pressão medidos são lidos sequencialmente na porta COM virtual e filtrados. Os valores medidos e filtrados do parâmetro medido em tempo real são exibidos na janela gráfica e no console. Os resultados do experimento são registrados pela tabela em um arquivo e as linhas do tempo dos valores medidos e filtrados são exibidas na janela de desenho.
Listagem 2 import numpy as np import matplotlib.pyplot as plt import serial from drawnow import drawnow import datetime, time k = 6.0
Resultados da Experiência
: 33 : 6 : COM6 : n - ; P - , ; n P 0 100490.00 100490.00 1 100488.00 100489.71 2 100487.00 100489.33 3 100488.00 100489.14 4 100488.00 100488.97 … 30 100486.00 100488.14 31 100492.00 100488.70 32 100489.00 100488.74 : 16.028, c : 0.500875, c 275_count.txt Ctrl-C,
Conclusões
O algoritmo de filtragem acima é muito simples na implementação de software e, na prática, pode ser usado em IICs semelhantes às discutidas neste artigo.
Losikhin D.A., s.v. café CITYM .
Fontes de informação
- Sensor de pressão digital BMP280
- Filtro de resposta ao impulso infinito