Nesta série de artigos, você se familiarizará com os princípios básicos da programação funcional e entenderá o que significa "pensar funcionalmente" e como essa abordagem difere da programação orientada a objetos ou imperativa.

Agora que você já viu alguns dos motivos pelos quais deveria usar o F #, no artigo “ Mergulhando no F #. Um Guia para Desenvolvedores de C # ”, dê um passo atrás e discuta os conceitos básicos de programação funcional. O que realmente significa “programação funcional” e como essa abordagem difere da programação orientada a objetos ou imperativa?
Mudança de mentalidade (Introdução)
É importante entender que a programação funcional não é apenas um estilo de programação separado. Essa é uma maneira completamente diferente de pensar em programação, que difere da abordagem “tradicional” tão significativamente quanto a OOP atual (no estilo Smalltalk) difere de uma linguagem imperativa tradicional como C.
O F # permite que você use estilos de codificação não funcionais, e isso tenta o programador a preservar seus hábitos existentes. Você pode programar em F # do jeito que está acostumado, sem alterar radicalmente a visão de mundo e sem nem mesmo saber o que está perdendo. No entanto, para tirar o máximo proveito do F # e também aprender como programar com confiança em um estilo funcional em geral, é muito importante aprender a pensar de uma maneira funcional e não imperativa.
O objetivo desta série de artigos é ajudar o leitor a entender os antecedentes da programação funcional e mudar sua maneira de pensar.
Esta será uma série bastante abstrata, embora eu use muitos exemplos de código curto para demonstrar alguns pontos. Abordaremos os seguintes tópicos:
- Funções matemáticas . O primeiro artigo apresenta os conceitos matemáticos subjacentes às linguagens funcionais e os benefícios que essa abordagem traz.
- Funções e valores . A seguir, são apresentadas funções e valores, explica como os "valores" diferem das variáveis e quais são as semelhanças entre funções e valores simples.
- Tipos . Em seguida, passamos aos tipos principais que funcionam com funções: tipos primitivos, como string e int, tipo de unidade, tipos funcionais e tipos genéricos.
- Funções com vários parâmetros . Vou explicar melhor os conceitos de "currying" e "aplicação parcial". Nesse lugar, o cérebro de alguém será ferido, especialmente se esses cérebros tiverem um passado imperativo.
- Definição de funções . Em seguida, várias postagens serão dedicadas a muitas maneiras diferentes de definir e combinar funções.
- Assinaturas de funções . A seguir, é apresentado um post importante sobre o valor crítico das assinaturas de funções, o que elas significam e como usar assinaturas para entender o conteúdo das funções.
- Organização de funções . Quando fica claro como criar funções, surge a pergunta: como você pode organizá-las para torná-las acessíveis ao restante do código?
Funções matemáticas
A programação funcional é inspirada na matemática. As funções matemáticas possuem vários recursos muito interessantes que as linguagens funcionais tentam implementar.
Vamos começar com uma função matemática que adiciona 1 a um número.
Add1(x) = x+1
O que essa expressão realmente significa? Parece bem simples. Isso significa que existe uma operação que pega um número e adiciona 1 a ele.
Adicione alguma terminologia:
- O conjunto de valores válidos da função de entrada é chamado domínio (escopo). Neste exemplo, pode haver muitos números reais, mas tornaremos a vida mais simples e nos limitaremos aqui a números inteiros.
- O conjunto de resultados possíveis da função (faixa de valores) é chamado faixa (tecnicamente, a imagem do codomain ). Nesse caso, também há muitos números inteiros.
- Uma função é chamada de mapeamento (no mapa original) do domínio para o intervalo. (Ou seja, do escopo para o escopo.)
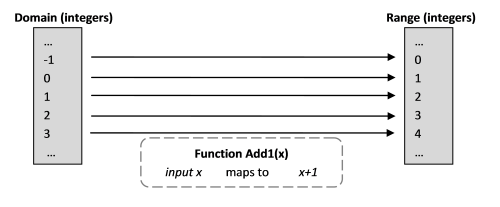
É assim que essa definição será exibida em F #.
let add1 x = x + 1
Se você o inserir no F # Interactive (não esqueça de ponto-e-vírgula duplo), poderá ver o resultado (a "assinatura" da função):
val add1 : int -> int
Considere a conclusão em detalhes:
- O significado geral é que a função
add1 compara números inteiros (do domínio de definição) com números inteiros (do intervalo de valores). - "
add1 " é definido como "val", abreviação de "value". Hum? o que isso significa Discutiremos os significados um pouco mais tarde. - A notação de seta “->” é usada para mostrar domínio e intervalo. Nesse caso, o domínio é do tipo 'int', como range.
Observe que o tipo não foi especificado explicitamente, mas o compilador F # decidiu que a função funciona com ints. (Isso pode ser alterado? Sim, e em breve veremos isso).
Propriedades principais das funções matemáticas
As funções matemáticas têm várias propriedades que as distinguem muito das funções usadas na programação procedural.
- Uma função sempre tem o mesmo resultado para o mesmo valor de entrada.
- A função não tem efeitos colaterais.
Essas propriedades fornecem uma série de vantagens notáveis que as linguagens de programação funcional tentam obter o máximo possível em seu design. Vamos considerar cada um deles por vez.
Funções matemáticas sempre retornam o mesmo resultado a um determinado valor
Na programação imperativa, pensamos que as funções “fazem” algo ou “contam” algo. As funções matemáticas não contam nada, são mapeamentos puros da entrada para a saída. De fato, outra definição de uma função é um conjunto simples de todos os mapeamentos. Por exemplo, é muito rudemente possível definir a função "add1" (em C #) como
int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } }
Obviamente, é impossível ter um argumento para todos os números possíveis, mas o princípio é o mesmo. Com essa configuração, nenhum cálculo é realizado, apenas uma pesquisa é realizada.
Funções matemáticas livres de efeitos colaterais
Em uma função matemática, os valores de entrada e saída são logicamente duas coisas diferentes, sendo ambas predefinidas. A função não altera os dados de entrada ou saída e simplesmente mapeia o valor de entrada predefinido da área de definição para o valor de saída predefinido na área de valor.
Em outras palavras, um cálculo de função não pode ter nenhum efeito nos dados de entrada ou em qualquer outra coisa do tipo . Deve-se lembrar que o cálculo de uma função realmente não conta ou manipula nada, é apenas uma pesquisa sobrestimada.
Essa “imutabilidade” de valores é muito sutil, mas ao mesmo tempo uma coisa muito importante. Quando faço contas, não espero que os números mudem à medida que são adicionados. Por exemplo, se eu tiver:
x = 5 y = x+1
Não espero que x mude ao adicionar 1. Espero obter um número diferente ( y ) e x permaneça intocado. No mundo da matemática, os números inteiros já existem em um conjunto imutável, e a função add1 simplesmente determina a relação entre eles.
O poder da função pura
Esses tipos de funções que têm resultados repetíveis e não têm efeitos colaterais são chamados de "funções puras" e você pode fazer algumas coisas interessantes com eles:
- Eles são fáceis de paralelizar. Digamos, podemos pegar números inteiros no intervalo de 1 a 1000 e distribuí-los para 1.000 processadores diferentes, após o que instruímos cada CPU a executar "
add1 " no número correspondente, ao mesmo tempo em que add1 que não há necessidade de interação entre eles. Sem bloqueios, sem mutexes, sem semáforos, etc. - Você pode usar funções preguiçosamente, calculando-as quando necessário para a lógica do programa. Você pode ter certeza de que a resposta será exatamente a mesma, independentemente de os cálculos serem realizados agora ou mais tarde.
- Você só pode executar cálculos de funções para uma entrada específica e, em seguida, armazenar em cache o resultado, porque é sabido que esses valores de entrada fornecerão a mesma saída.
- Se houver muitas funções puras, elas podem ser calculadas em qualquer ordem. Novamente, isso não pode afetar o resultado final.
Assim, se é possível criar funções puras em uma linguagem de programação, você pode receber imediatamente muitos truques poderosos. E, sem dúvida, tudo isso pode ser feito em F #:
- Um exemplo de computação paralela estava na série "Por que usar F #?" .
- O cálculo da função preguiçosa será discutido na série Otimização .
- Os resultados da função de armazenamento em cache são chamados de memorização e também serão discutidos na série Otimização .
- A ausência da necessidade de rastrear a ordem de execução facilita muito a programação paralela e elimina a necessidade de erros causados pela alteração da ordem das funções ou refatoração.
Propriedades "inúteis" de funções matemáticas
As funções matemáticas também possuem algumas propriedades que parecem pouco úteis na programação.
- Os valores de entrada e saída são imutáveis
- As funções sempre têm uma entrada e uma saída.
Essas propriedades são refletidas no design de linguagens de programação funcionais. Vale a pena considerá-los separadamente.
Os valores de entrada e saída são imutáveis
Valores imutáveis na teoria parecem uma boa idéia, mas como qualquer trabalho pode realmente ser feito se não há como atribuir uma variável da maneira tradicional.
Posso garantir que esse não é um problema tão grande como você pode imaginar. Nesta série de artigos, ficará claro como isso funciona na prática.
As funções matemáticas sempre têm uma entrada e uma saída.
Como pode ser visto nos diagramas, para uma função matemática, sempre há apenas uma entrada e apenas uma saída. Isso também é válido para linguagens de programação funcionais, embora possa não ser óbvio quando usado pela primeira vez.
Isso parece ser um grande inconveniente. Como posso fazer algo útil sem funções com dois (ou mais) parâmetros?
Acontece que existe uma maneira de fazer isso e, além disso, é completamente transparente no F #. É chamado de "currying" e merece um post separado, que aparecerá em um futuro próximo.
De fato, mais tarde ficará claro que essas duas propriedades "inúteis" se tornarão incrivelmente valiosas e serão a parte principal que torna a programação funcional tão poderosa.
Recursos Adicionais
Existem muitos tutoriais para F #, incluindo materiais para quem vem com experiência em C # ou Java. Os links a seguir podem ser úteis à medida que você avança no F #:
Várias outras maneiras de começar a aprender F # também são descritas.
Finalmente, a comunidade F # é muito amigável para iniciantes. Há um bate-papo muito ativo no Slack, suportado pela F # Software Foundation, com salas para iniciantes nas quais você pode participar livremente . É altamente recomendável que você faça isso!
Não se esqueça de visitar o site da comunidade de língua russa F # ! Se você tiver alguma dúvida sobre o aprendizado de um idioma, teremos prazer em discuti-los nas salas de bate-papo:
Sobre autores de tradução
Traduzido por @kleidemos
 As mudanças de tradução e editoriais foram feitas pelos esforços da comunidade de desenvolvedores de F # de língua russa . Agradecemos também a @schvepsss e @shwars pela preparação deste artigo para publicação.
As mudanças de tradução e editoriais foram feitas pelos esforços da comunidade de desenvolvedores de F # de língua russa . Agradecemos também a @schvepsss e @shwars pela preparação deste artigo para publicação.