A dinâmica do vôo vertical de uma aeronave mais leve que o ar

1. Introdução

Determinar a velocidade de subida e descida de aeronaves mais leves que o ar (LALV) até o momento é quase uma tarefa importante que surge no design desses dispositivos.

Um grande número de publicações é dedicado ao LALF, por exemplo, apenas em nosso recurso há dois artigos muito interessantes [1,2] relacionados à história do desenvolvimento no exemplo de projetos específicos de aeronaves e estratostatos. No entanto, existem muito poucos cálculos da dinâmica do voo vertical de tais dispositivos, permitindo pelo menos determinar aproximadamente a velocidade de subida e descida das ALPC.

A última afirmação requer certa explicação, uma vez que um leitor experiente se lembra do curso de física da escola, no qual foram resolvidos problemas na altura da subida e outros parâmetros de balões cheios de gases mais leves que o ar ou pelo próprio ar aquecido durante o vôo.

Todas essas tarefas foram baseadas na igualdade de duas forças: a força do peso e a força de flutuação. Os gases foram considerados ideais e seus parâmetros foram calculados de acordo com a lei de Mendeleev Clapeyron. Contudo, mesmo um simples cálculo da terceira força de resistência do ar já leva a um sistema de equações diferenciais, que não podem ser resolvidas analiticamente. Também é necessário levar em consideração a mudança na densidade do ar atmosférico com a altura da subida e a temperatura.

Além disso, se você precisar considerar não apenas a ascensão, mas também o congelamento da bola e sua descida ao chão, isso não é tarefa das crianças. Espero que a consideração da solução de um problema semelhante por meio do Python não apenas contribua para a expansão do conhecimento em física, mas também para a popularização da própria linguagem de programação Python. O que tento fazer nas minhas publicações sobre este recurso.

Um modelo matemático do voo de um LALV com uma concha no formato de uma bola, cujo volume não muda com a altura

Nós nos restringimos a considerar o movimento de seu centro de massa sob a ação das seguintes forças: gravidade ( G ), força arquimediana ( Fa ) e força aerodinâmica de arrasto ( Fc ). Escrevemos as relações para determinar as forças através dos parâmetros do movimento e do ambiente aéreo [3]:





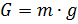
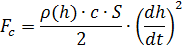
Nas fórmulas acima, a notação é usada: h é a altura da bola, dh / dt é a velocidade vertical, m é a massa, g é a aceleração da gravidade, W é o volume da bola, c é o volume da bola, c é o coeficiente de arrasto, S é a área de resistência característica (área intermediária).
A dependência da densidade do ar na altura será assumida como exponencial:



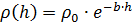
onde $$$ρ_0$- densidade do ar à altura zero, b - coeficiente. A força da gravidade é direcionada para baixo, a força arquimediana é direcionada para cima e a força do arrasto aerodinâmico é sempre direcionada “contra o movimento”, portanto, a inclusão correta dessa força nas equações de movimento requer a introdução de um fator $$$-sing (dh / dt)$.

No entanto, para nossos propósitos, esse fato não é de fundamental importância, e nos restringimos a considerar apenas o estágio de elevação da bola, quando a força de arrasto aerodinâmica é direcionada para baixo e, portanto, será levada em consideração nas equações de movimento com um sinal de menos. Agora a equação do movimento pode ser escrita como:

(1)

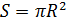
Além disso, suponha que o balão seja um corpo homogêneo de raio R com densidade $$$ρ_b$. Em seguida, o tamanho da área que determina seu arrasto aerodinâmico é definido como volume como e massa, respectivamente, como .

Agora está claro que cada termo da equação (1) contém S. como fator, portanto, cada termo da equação de movimento pode ser reduzido por um fator de S. A própria equação assumirá a forma:

(2)

Introduzimos a seguinte notação:

;
;

e reescreva (2) na forma do seguinte sistema de equações não lineares:

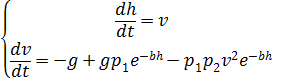
(3)

Influência na velocidade e altura da elevação da temperatura do ar LALV

Para fazer isso, primeiro resolvemos o sistema (3) usando a seguinte relação para a dependência da densidade do ar atmosférico na altura, sem levar em conta a temperatura:



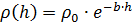
Vamos repetir a solução do sistema (3), mas usando a relação para a dependência da densidade do ar em altitude e temperatura:



onde: b = 0,000125 é uma constante associada a uma densidade do ar de 1 / m;
a = 0,0065 é uma constante relacionada à temperatura do ar em K / m.
$$$T_0 = $ 300 K$- temperatura ao nível do mar.


Temos:



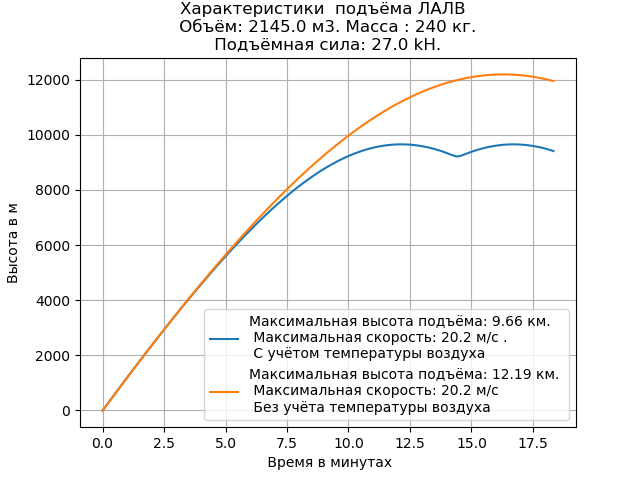
O valor calculado da altura do elevador LALV, levando em consideração a temperatura, é menor do que sem levar em consideração. A velocidade de elevação do aparelho permanece inalterada.

Determinação das características de todas as fases do voo SALV do início ao pouso

Para criar o programa de voo LALV, considere as condições para os seguintes períodos:

Ascensão - ;
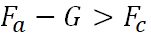
Pendure - ;
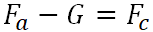
Aterragem - .


Temos:



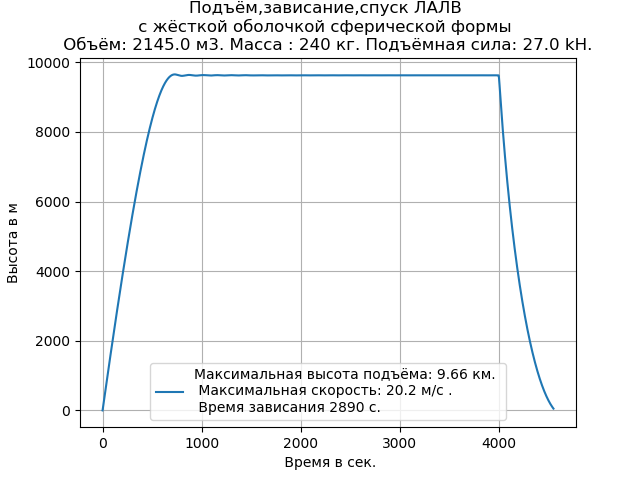
Como se segue no gráfico e na lista do programa, para realizar um experimento computacional, basta inserir os dados iniciais necessários.

Um modelo matemático do voo de um LALV com casca, cujo volume varia com a altura

Tais LALV incluem estratostatos. O balão estratosférico não pode ser completamente inflado com hélio, proporcionando força máxima de elevação, que transformará a forma de sua concha em uma bola. Essa bola em alta altitude pode estourar devido ao aumento da diferença nas pressões internas e externas.

Por esses motivos, para calcular a altura máxima de elevação atingível, são introduzidos dois valores de seu volume: o Vmin mínimo e o Vmax máximo, respectivamente. Tendo em conta as variáveis ​​introduzidas e a dependência da densidade do ar em relação à altura, as relações entre a força de flutuação Fa e a força de gravidade Ft assumem a forma:

(4)

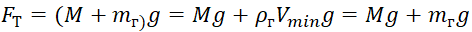
(5)

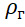
onde: M é a massa da concha e o equipamento do balão estratosférico; É a densidade do hélio.

Equacionando as relações (4) e (5), assumindo que o volume da concha V é uma função da altura do LALV, obtemos a razão:

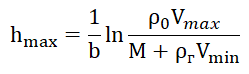
. (6)

Os valores numéricos dos parâmetros incluídos na relação (6) são dados na listagem para a construção de um gráfico, que é fornecido apenas para a finalidade indicada.


Temos:



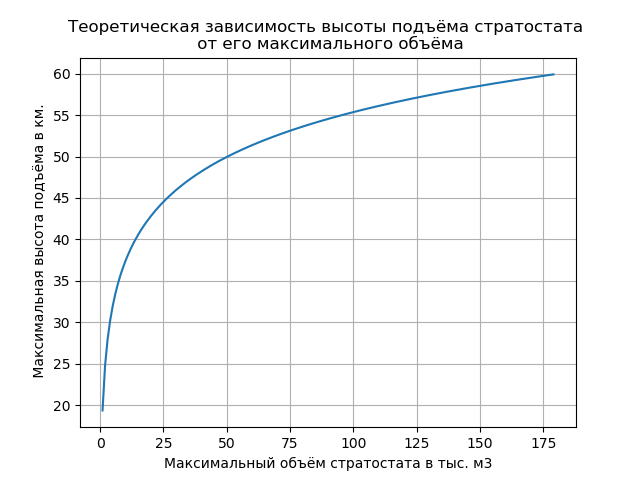
Alterando os parâmetros LALV listados na lista de programas, você pode obter o gráfico fornecido e selecionar o volume máximo de shell necessário durante o design. O refinamento dos resultados é realizado com vasta experiência na criação de tais dispositivos.

Conclusões:

1. Modelos matemáticos de dois tipos de aeronaves mais leves que o ar são obtidos, o que permite que experimentos computacionais avaliem os parâmetros de tais dispositivos em condições idealizadas do ambiente aéreo.
   
2. O esquema de estágios proposto para a solução numérica do sistema de equações diferenciais permite obter a trajetória vertical de aeronaves mais leves que o ar nos estágios da ascensão de pairar e descer.
   

Referências

1. Algumas palavras sobre aeronaves
   
2. A caminho do espaço. Stratostats
   
3. Ryzhikov Yu.I. Fortran moderno. - São Petersburgo: Crown print, 2004 - 288 p.