Os matemáticos refutaram a hipótese da existência de um forte princípio de censura cósmica. O trabalho deles responde a uma das questões mais importantes no estudo da teoria geral da relatividade e muda a maneira como falamos sobre espaço-tempo.
Quase 40 anos após sua formulação, os matemáticos decidiram sobre uma das questões mais destacadas no estudo da teoria geral da relatividade. Em um
artigo publicado na Internet no outono passado, os matemáticos
Michalis Dafermos e
Jonathan Luck provaram que a forma forte do
princípio da censura cósmica relacionada à estranha estrutura dos buracos negros está incorreta.
"Pessoalmente, considero este trabalho uma conquista incrível - um salto qualitativo em nossa compreensão da relatividade geral", escreveu-me
Igor Rodnyansky , matemático da Universidade de Princeton.
Uma poderosa forma do princípio da censura espacial foi proposta em 1979 pelo influente físico Roger Penrose. Era uma maneira de escapar da armadilha. Por décadas de relatividade geral, Albert Einstein governou como a melhor descrição científica dos fenômenos de larga escala do universo. No entanto, as realizações matemáticas da década de 1960 mostraram que as equações de Einstein encontraram inconsistências desagradáveis quando aplicadas a buracos negros. Penrose acreditava que, se seu forte princípio de censura cósmica for verdadeiro, a falta de previsibilidade pode ser ignorada, considerando-a uma característica matemática e não uma descrição real do mundo físico.
"Penrose apresentou uma hipótese que essencialmente tentou se livrar magicamente de um comportamento tão desagradável", disse Dafermos, matemático de Princeton.
Um novo trabalho quebra o sonho de Penrose. Ao mesmo tempo, ela cumpre suas ambições de outras maneiras, mostrando que seu entendimento intuitivo do interior do buraco negro estava correto, simplesmente não pelos motivos pelos quais suspeitava.
O pecado mortal da relatividade
Na física clássica, o universo é previsível. Se você conhece as leis que governam o sistema físico e seu estado inicial, deve poder acompanhar seu desenvolvimento até o infinito. Essa máxima funciona se você está tentando usar as leis de Newton para prever a posição futura de uma bola de bilhar, a equação de Maxwell para descrever o campo eletromagnético ou a GRT de Einstein para prever a evolução da forma espaço-temporal. "Esse é o princípio básico de toda a física clássica, que pode ser rastreada até a mecânica newtoniana", disse
Demetrios Hristodulu , matemático da ETH Zurique e especialista líder no estudo das equações de Einstein. "A evolução pode ser determinada com base nos dados iniciais."
Mas na década de 1960, os matemáticos descobriram um cenário físico no qual as equações de campo gravitacional de Einstein - formando o núcleo de seu GR - cessam de descrever um universo previsível. Matemáticos e físicos notaram que algo dá errado quando modelaram a evolução do espaço-tempo dentro de um buraco negro em rotação.
Para entender o que deu errado, imagine-se caindo em um buraco negro. Primeiro, você cruza o horizonte de eventos, o ponto sem retorno (embora para você não seja diferente do espaço comum). Aqui, as equações de Einstein ainda funcionam como deveriam, fornecendo uma previsão única e determinística de como o espaço-tempo mudará no futuro.
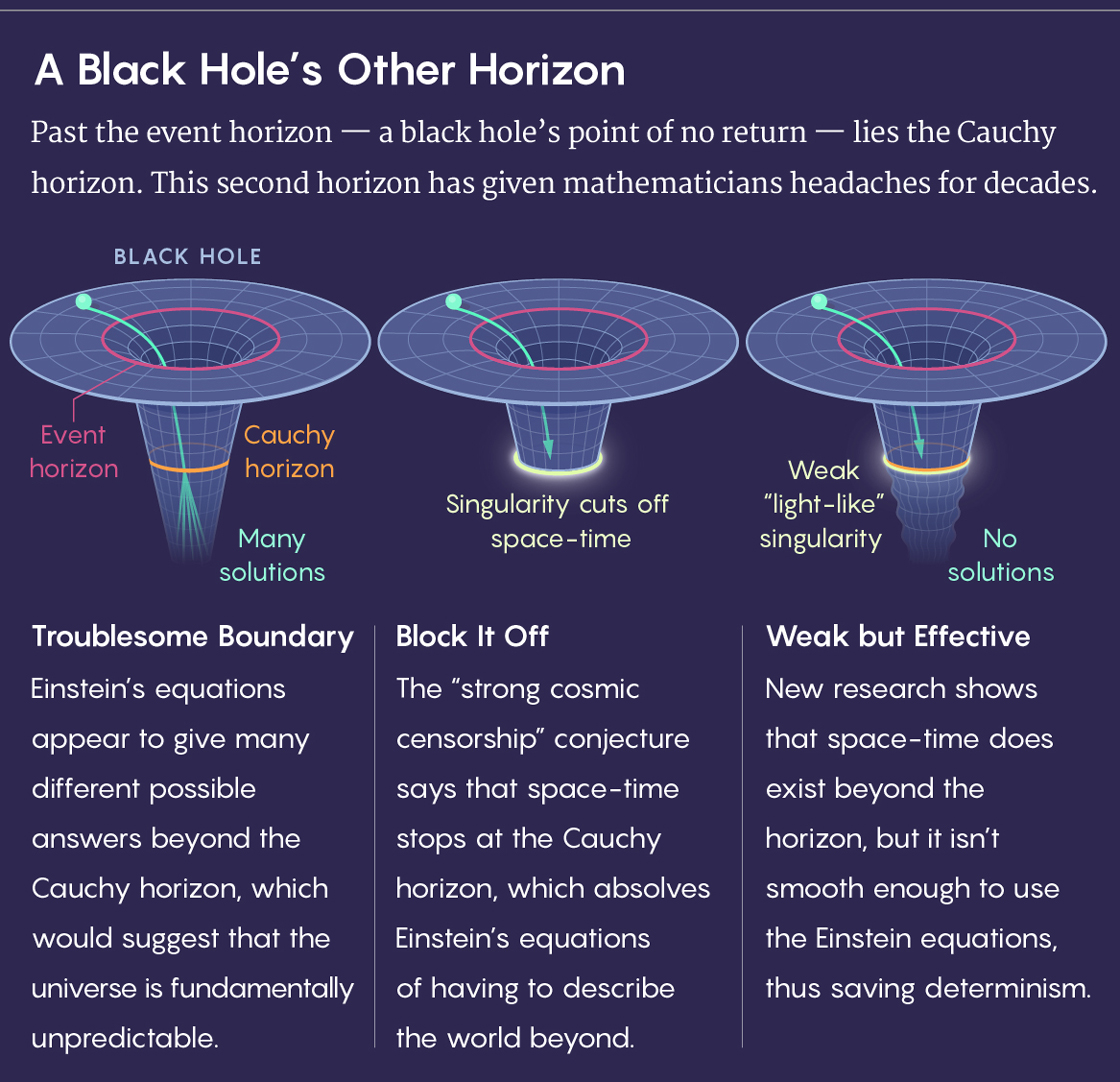Além do ponto de não retorno do BH, fica o segundo horizonte - o horizonte de Cauchy . As equações de Einstein oferecem muitas opções para soluções além do horizonte de Cauchy, o que significaria que o Universo é fundamentalmente imprevisível.
O forte princípio da censura cósmica diz que o espaço-tempo termina no horizonte de Cauchy, de modo que as equações de Einstein não precisam descrever mais o mundo.
Mas um novo estudo mostra que além desse horizonte há espaço-tempo, porém não é suficientemente suave para usar as equações de Einstein - isso preserva a previsibilidade.Se você continuar sua jornada dentro de BH, acabará cruzando outro horizonte, conhecido como horizonte de Cauchy. E então tudo fica louco. As equações de Einstein começam a produzir muitas variações do espaço-tempo. Todos eles diferem um do outro, mas satisfazem as equações. A teoria não pode dizer qual opção estará correta. Para a teoria física, este é um pecado mortal.
"A perda de previsibilidade que parecemos ver na relatividade geral foi muito desagradável", disse
Eric Poisson , físico da Universidade de Guelph, no Canadá.
Roger Penrose propôs o forte princípio da censura cósmica para restaurar a previsibilidade nas equações de Einstein. Diz que o horizonte de Cauchy é uma construção puramente matemática. Poderia existir em um cenário ideal em que não há nada no Universo, exceto um único buraco negro rotativo, mas não pode existir na realidade.
A razão para isso, em sua opinião, era que o horizonte de Cauchy é instável. Ele disse que qualquer onda gravitacional que passasse por ela deveria provocar seu colapso em uma singularidade - em uma seção de densidade infinita, rasgando o espaço-tempo. Como o universo real está cheio dessas ondas, o horizonte de Cauchy não deve aparecer na natureza.
Como resultado, não faz sentido perguntar o que acontece com o espaço-tempo além do horizonte de Cauchy, uma vez que o espaço-tempo, conforme descrito na estrutura de GR, deixa de existir. "Esta é uma maneira de sair desse quebra-cabeça", disse Dafermos.
Mas este novo trabalho mostra que o limite de espaço-tempo definido pelo horizonte de Cauchy tem menos a ver com singularidade do que Penrose imaginava.
Salve o buraco negro
Dafermos e Luck, um matemático de Stanford, provaram que a situação no horizonte de Cauchy não é tão simples. O trabalho deles refuta astuciosamente a carta da declaração inicial de Penrose sobre a censura espacial, mas não rejeita completamente seu espírito.
Com base em métodos desenvolvidos há dez anos por Christodoulou, ex-mentor da Dafermos no instituto, o casal mostrou que o horizonte de Cauchy poderia de fato formar uma singularidade, mas não o que Penrose esperava. A singularidade em seu trabalho não é tão nítida quanto a de Penrose - eles encontraram uma singularidade fraca e "leve", na qual esperavam encontrar uma "espacial". Uma forma mais fraca de singularidade atrai o tecido do espaço-tempo, mas não o rasga. “Nosso teorema diz que os observadores que cruzam o horizonte de Cauchy não são despedaçados pelas forças das marés. Eles podem sentir a injeção, mas não rasgam ”, disse Dafermos pelo correio.
Como a singularidade que se forma no horizonte de Cauchy é mais suave do que a que prevê o forte princípio da censura cósmica, a GTR não proíbe prever o que está acontecendo lá dentro. "Ainda faz sentido determinar o horizonte de Cauchy, porque podemos, se quisermos, prolongar continuamente o espaço-tempo além dele", disse
Harvey Rial , físico da Universidade de Cambridge.
Dafermos e Luck provaram que o espaço-tempo se estende além do horizonte de Cauchy. Eles também provaram que, do mesmo ponto de partida, pode continuar de maneiras diferentes. Além do horizonte, "existem muitas continuações que podem ser consideradas e não há razão para preferir uma delas à outra", disse Dafermos.
Contudo - e aqui está o truque de seu trabalho - essas extensões não-únicas do espaço-tempo não significam que as equações de Einstein rompam além do horizonte.
As equações de Einstein funcionam medindo as mudanças no espaço-tempo ao longo do tempo. Em termos matemáticos, é necessário obter derivadas da configuração inicial do espaço-tempo. E, para obter a derivada, é necessário que o espaço-tempo seja suficientemente “suave” - livre de descontinuidades. Dafermos e Luck mostram que, embora o espaço-tempo exista além do horizonte de Cauchy, esse espaço-tempo estendido não será suave o suficiente para satisfazer as equações de Einstein. Portanto, embora o forte princípio da censura cósmica tenha sido refutado, as equações estão livres da vergonha de emitir soluções não exclusivas.
“Faz sentido falar sobre o horizonte de Cauchy; no entanto, você não pode aceitá-lo como parte da solução das equações de Einstein, disse Rial. "Acho que eles ofereceram evidências convincentes de que isso é verdade".
Esse resultado pode ser imaginado como um compromisso desagradável: embora seja possível continuar o espaço-tempo além do horizonte de Cauchy, as equações de Einstein não podem ser resolvidas. Mas é precisamente o fato da existência de tal compromisso que torna o trabalho de Dafermos e Luck tão interessante.
"De fato, um novo fenômeno foi descoberto nas equações de Einstein", disse Rodnyansky.