Por que os físicos pensam que a teoria das cordas pode se tornar "a teoria de tudo"

A teoria das cordas é baseada na ideia de que, em vez de partículas elementares de dimensão zero, o Universo consiste em cordas unidimensionais

A teoria das cordas é uma das idéias mais brilhantes, contraditórias e não comprovadas da física. É baseado em uma tendência física que viveu por muitos séculos - que em algum nível fundamental, todas as várias forças, partículas, interações e manifestações da realidade estão ligadas entre si como partes diferentes de uma plataforma. Em vez de quatro interações fundamentais independentes - forte, eletromagnética, fraca e gravitacional - existe uma teoria unificada que abrange todas elas.

De muitas maneiras, a teoria das cordas é a melhor candidata à teoria quântica da gravidade, combinando interações nos níveis mais altos de energia. Embora não exista evidência experimental para isso, existem razões teóricas convincentes para acreditar que é assim. Em 2015, o maior especialista em teoria das cordas vivas, Edward Witten, escreveu um artigo sobre o que todo físico deveria saber sobre a teoria das cordas. E aqui está o que isso significa - mesmo que você não seja físico.


A diferença entre as interações padrão da teoria quântica de campos (esquerda) para partículas pontuais e as interações na teoria de cordas (direita) para cordas fechadas.

É surpreendente como às vezes muitas semelhanças são encontradas nas leis da natureza relacionadas a fenômenos aparentemente não relacionados. As estruturas matemáticas de tais fenômenos são frequentemente muito semelhantes e, às vezes, até idênticas. A atração de dois corpos maciços de acordo com as leis de Newton é quase idêntica à atração / repulsão de partículas eletricamente carregadas. As oscilações do pêndulo são completamente análogas ao movimento de massa em uma mola ou planeta ao redor de uma estrela. Ondas gravitacionais, ondas de água, ondas de luz - todas elas têm propriedades surpreendentemente semelhantes, apesar de serem provenientes de fontes físicas fundamentalmente diferentes. E na mesma linha, embora muitos não percebam isso, a teoria quântica de uma partícula e a abordagem da teoria quântica da gravidade também são semelhantes entre si.


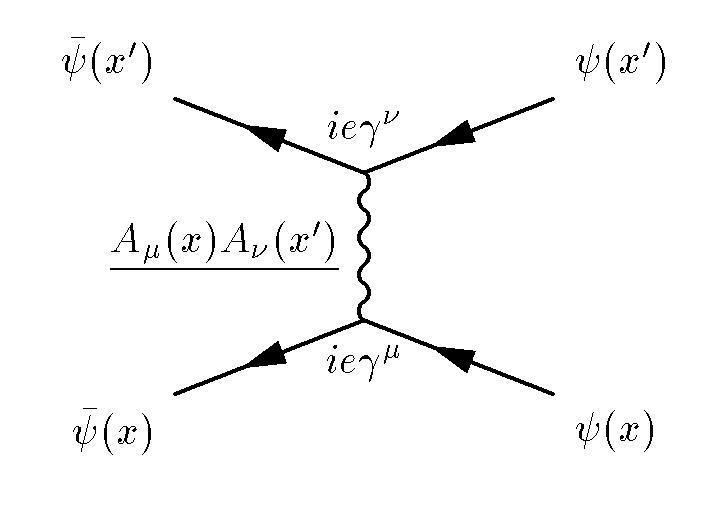Diagrama de Feynman representando a dispersão de dois elétrons - para isso é necessário resumir todas as histórias possíveis de interações de partículas

A teoria quântica de campos funciona assim: pegue uma partícula e faça o "somatório de todas as suas histórias" em matemática. Você não pode apenas calcular onde a partícula estava, onde está agora e como chegou lá - porque na natureza há uma incerteza quântica interna e fundamental. Em vez disso, resumimos todas as maneiras possíveis pelas quais ele poderia chegar ao estado atual (“histórico passado”), com os correspondentes pesos probabilísticos, e depois calculamos o estado quântico de uma partícula.

Para trabalhar com a gravidade, e não com partículas quânticas, você precisa mudar um pouco. Como a Teoria Geral da Relatividade de Einstein está associada não a partículas, mas à curvatura do espaço-tempo, não calcularemos a média de todas as histórias possíveis de partículas. Em vez disso, calculamos a média de todas as geometrias possíveis de espaço-tempo.


A gravidade de acordo com as regras de Einstein e tudo o mais (interações fortes, fracas e eletromagnéticas) de acordo com as regras da física quântica são dois conjuntos diferentes de leis que governam tudo no universo.

Trabalhar em três dimensões espaciais é muito difícil e, quando encontramos um problema físico complexo, geralmente tentamos resolver uma versão mais simples dele primeiro. Se você descer uma dimensão, tudo ficará mais fácil. As únicas superfícies unidimensionais possíveis são uma cadeia aberta, com duas extremidades separadas que não estão conectadas entre si, ou uma cadeia fechada, cujas extremidades estão conectadas e formam um loop. Além disso, a curvatura do espaço - muito complexa em três dimensões - se torna uma questão trivial. Portanto, se queremos adicionar matéria, usamos um conjunto de campos escalares (como para um certo tipo de partículas) e uma constante cosmológica (funcionando exatamente como um membro da equação responsável pela massa): uma analogia maravilhosa.

Os graus adicionais de liberdade que uma partícula recebe em várias dimensões não desempenham um papel especial; contanto que possamos determinar o vetor de momento, essa continua sendo a dimensão principal. Portanto, em uma dimensão, a gravidade quântica se parece com uma partícula quântica livre em qualquer número arbitrário de dimensões.


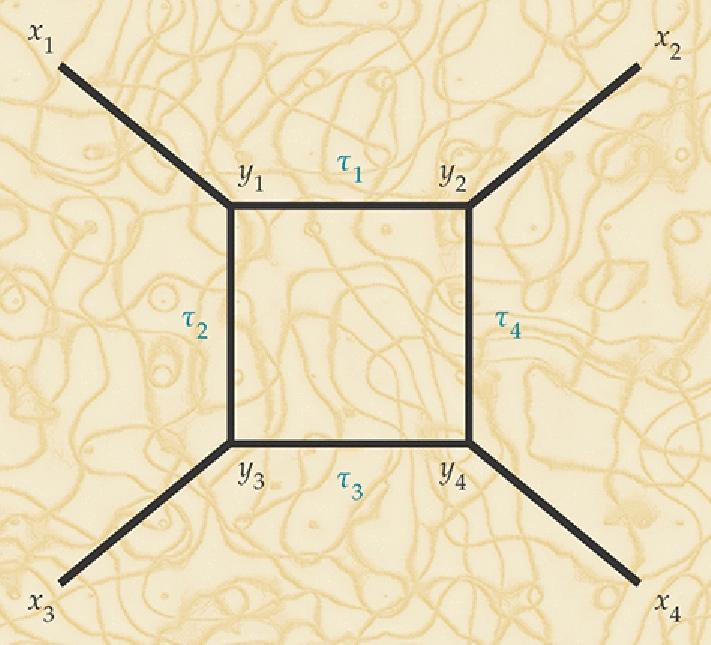Um gráfico com vértices onde três arestas convergem é um componente essencial da construção da integral do caminho relacionada à gravidade quântica unidimensional

O próximo passo é ativar as interações e passar de uma partícula livre sem amplitudes de dispersão ou seções transversais efetivas para uma que possa ter um papel físico associado ao universo. Gráficos semelhantes ao acima permitem descrever o conceito físico de ação em gravidade quântica. Se escrevermos todas as combinações possíveis de tais gráficos e as resumirmos - usando as mesmas leis de sempre, por exemplo, a lei de conservação do momento -, podemos concluir a analogia. A gravidade quântica em uma dimensão é muito semelhante à interação de uma partícula em qualquer número de dimensões.


A probabilidade de detectar uma partícula quântica em um determinado local nunca é 100%; a probabilidade é distribuída no espaço e no tempo.

O próximo passo é passar de uma dimensão espacial para 3 + 1 dimensões: para onde o Universo tem três dimensões espaciais e uma temporal. Mas essa "atualização" teórica da gravidade pode ser muito difícil. Uma abordagem diferente pode ser encontrada se decidirmos trabalhar na direção oposta.

Em vez de contar o comportamento de uma partícula (entidade de dimensão zero) em qualquer número de dimensões, talvez pudéssemos contar o comportamento de uma corda, aberta ou fechada (entidade de uma dimensão). E com base nisso, já procure analogias com uma teoria mais completa da gravidade quântica em um número mais realista de dimensões.


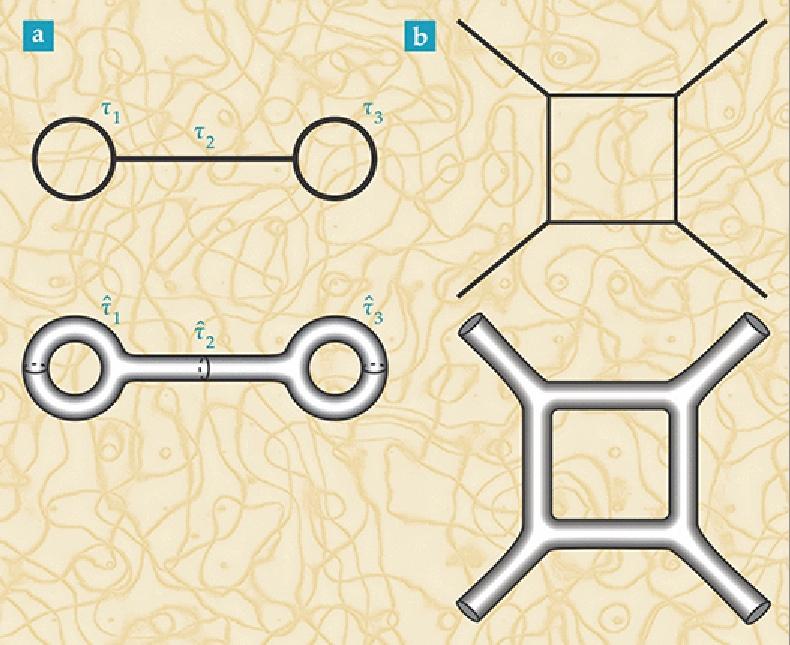Os diagramas de Feynman (acima) são baseados em partículas pontuais e suas interações. Transformando-os em análogos para a teoria das cordas (abaixo), obtemos superfícies que podem ter curvatura não trivial.

Em vez de pontos e interações, começamos imediatamente a trabalhar com superfícies, membranas e assim por diante. Tendo obtido uma verdadeira superfície multidimensional, podemos dobrá-la de maneiras não triviais. Começamos a observar seu comportamento muito interessante; um que pode ser a base da curvatura do espaço-tempo observada no Universo no âmbito da GR.

Porém, embora a gravidade quântica unidimensional nos dê uma teoria quântica de campos para partículas no espaço-tempo possivelmente curvo, ela sozinha não descreve a gravidade. O que está faltando neste quebra-cabeça? Não há correspondência entre operadores ou funções que representam interações e propriedades da mecânica quântica, bem como estados, isto é, como as partículas e suas propriedades mudam ao longo do tempo. Essa correspondência de "operadores estatais" era um ingrediente necessário, mas ausente.

Mas se passarmos de partículas pontuais para entidades de cadeia, essa correspondência se manifesta.


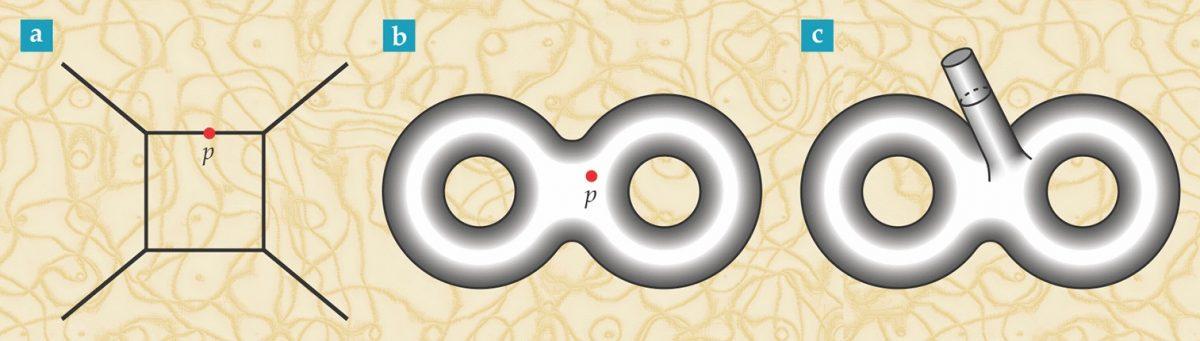A deformação da métrica espaço-tempo pode ser representada por uma flutuação ('p') e, se aplicada à analogia da corda, descreverá a flutuação do espaço-tempo e corresponderá ao estado quântico da corda.

Na transição de partículas para cordas, uma correspondência real de estados de operador aparece. A flutuação na métrica espaço-tempo (ou seja, o operador) representa automaticamente o estado na descrição da mecânica quântica das propriedades da string. Portanto, a teoria quântica da gravidade no espaço-tempo pode ser criada com base na teoria das cordas.

Mas isso não é tudo o que obtemos: também obtemos gravidade quântica, combinada com outras partículas e interações no espaço-tempo, com aquelas que correspondem a outros operadores de cordas na teoria de campos. Há também um operador que descreve flutuações na geometria espaço-temporal e outro para os estados quânticos da cadeia. A coisa mais interessante sobre a teoria das cordas é que ela pode nos dar uma teoria quântica de trabalho da gravidade.


Brian Green faz uma apresentação sobre a teoria das cordas

Tudo isso não significa que o problema tenha sido resolvido e que a teoria das cordas é o caminho para a gravidade quântica. A grande esperança da teoria das cordas é que essas analogias possam ser mantidas em todas as escalas e que exista uma correspondência individual inequívoca da imagem das cordas do mundo e do Universo que observamos ao nosso redor.

Até agora, a imagem do mundo com cordas e supercordas é consistente em apenas alguns conjuntos de dimensões, e a mais promissora delas não nos dá a gravidade quadridimensional de Einstein, que descreve nosso Universo. Em vez disso, descobrimos uma teoria da gravidade em 10 dimensões de Brans-Dicke . Para restaurar a gravidade existente em nosso Universo, é necessário "livrar-se" de seis dimensões e direcionar a constante de acoplamento ω para o infinito.

Se você ouviu o termo "compactação" aplicado à teoria das cordas, é apenas uma palavra que significa que devemos resolver esses enigmas. Até agora, muitas pessoas sugeriram uma solução completa e convincente adequada para compactar. Mas a questão de como obter a gravidade de Einstein e as dimensões 3 + 1 de uma teoria 10-dimensional permanece em aberto.


Projeção bidimensional do coletor Calabi-Yau , um dos métodos populares para compactar medidas adicionais e desnecessárias da teoria das cordas

A teoria das cordas oferece um caminho para a gravidade quântica com a qual poucas alternativas podem ser comparadas. Se tirarmos conclusões razoáveis ​​sobre como a matemática funciona, podemos extrair dela a relatividade geral e o modelo padrão. Hoje, essa é a única idéia que nos dá isso - portanto, é tão desesperadamente perseguida. Não importa se você defende o sucesso da teoria ou do fracasso das cordas, ou como se sente com a falta de previsões verificáveis, sem dúvida, continua sendo uma das áreas mais ativas de pesquisa em física teórica. De fato, a teoria das cordas se destaca como a idéia principal entre os sonhos dos físicos de uma teoria final.