AI, curso prático. Visão geral de redes neurais para classificação de imagens

Este artigo fornece uma visão geral teórica acessível de redes neurais convolucionais (CNN) e explica sua aplicação ao problema de classificação de imagens.

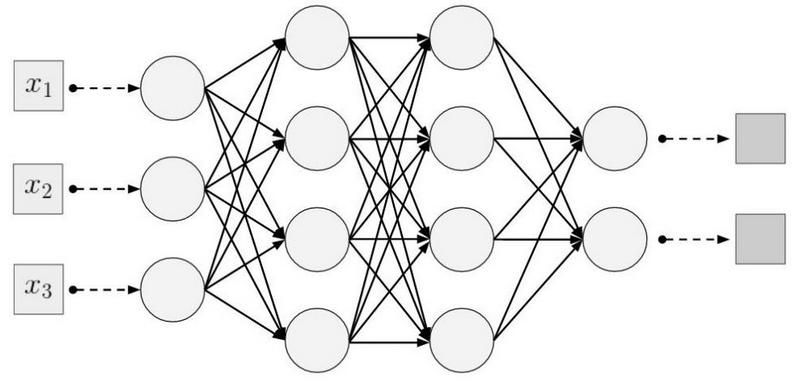
Abordagem comum: sem aprendizado profundo

O termo "processamento de imagem" refere-se a uma ampla classe de tarefas para as quais os dados de entrada são imagens e a saída pode ser imagens ou conjuntos de recursos característicos associados. Existem muitas opções: classificação, segmentação, anotação, detecção de objeto etc. Neste artigo, examinamos a classificação de imagens, não apenas por ser a tarefa mais simples, mas também por estar subjacente a muitas outras tarefas.

A abordagem geral para a classificação de imagens consiste nas duas etapas a seguir:

1. Geração de características significativas da imagem.
2. Classificação de uma imagem com base em seus atributos.

A sequência comum de operações usa modelos simples, como MultiLayer Perceptron (MLP), SVM (Support Vector Machine), método de vizinhos mais próximos e regressão logística sobre os recursos criados manualmente. Os atributos são gerados usando várias transformações (por exemplo, detecção de escala de cinza e limite) e descritores, por exemplo, histograma de gradientes orientados ( HOG ) ou transformações de transformadores de recurso invariáveis ​​em escala ( SIFT ) e etc.

A principal limitação dos métodos geralmente aceitos é a participação de um especialista que escolhe um conjunto e uma sequência de etapas para gerar recursos.

Com o tempo, percebeu-se que a maioria das técnicas para gerar recursos pode ser generalizada usando núcleos (filtros) - matrizes pequenas (geralmente com tamanho 5 × 5), que são convoluções das imagens originais. A convolução pode ser considerada como um processo seqüencial em duas etapas:

1. Passe o mesmo núcleo fixo por toda a imagem de origem.
2. Em cada etapa, calcule o produto escalar do kernel e a imagem original no local atual do kernel.

O resultado da convolução da imagem e do kernel é chamado de mapa de recursos.
Uma explicação matematicamente mais rigorosa é dada no capítulo relevante do livro recentemente publicado, Deep Learning, de I. Goodfellow, I. Benjio e A. Courville.


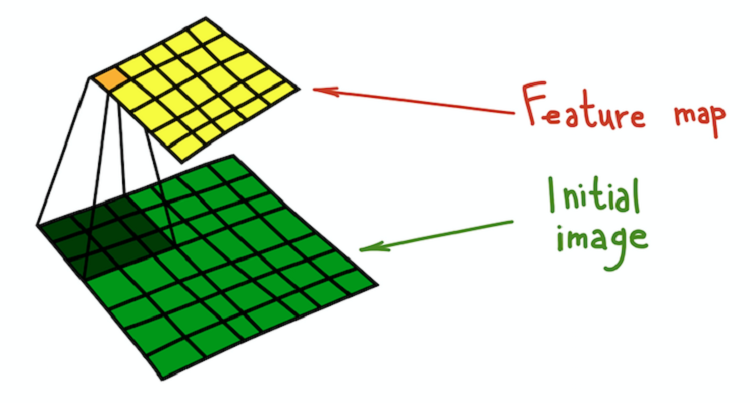O processo de convolução do núcleo (verde escuro) com a imagem original (verde), que resulta em um mapa de sinais (amarelo).

Um exemplo simples de uma transformação que pode ser feita com filtros é desfocar uma imagem. Pegue um filtro composto por todas as unidades. Calcula a média da vizinhança determinada pelo filtro. Nesse caso, o bairro é uma seção quadrada, mas pode ser cruciforme ou qualquer outra coisa. A média leva à perda de informações sobre a posição exata dos objetos, desfocando a imagem inteira. Uma explicação intuitiva semelhante pode ser fornecida para qualquer filtro criado manualmente.


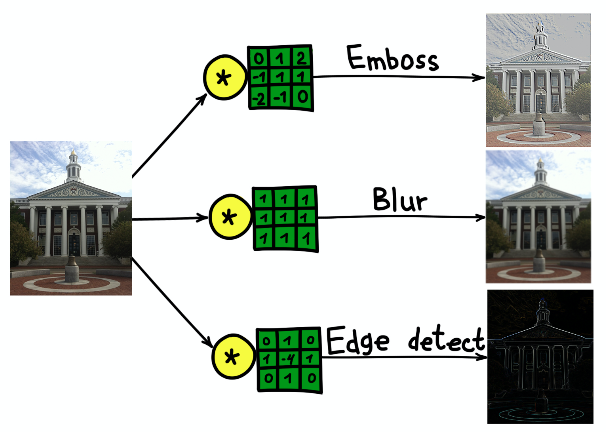O resultado da convolução da imagem do prédio da Universidade de Harvard com três núcleos diferentes.

Redes neurais convolucionais

A abordagem convolucional da classificação de imagens tem várias desvantagens significativas:

• Um processo de várias etapas em vez de uma sequência de ponta a ponta.
• Os filtros são uma ótima ferramenta de generalização, mas são matrizes fixas. Como escolher pesos nos filtros?

Felizmente, foram inventados filtros aprendíveis, que são o princípio básico subjacente à CNN. O princípio é simples: treinaremos os filtros aplicados à descrição das imagens para melhor cumprir sua tarefa.

A CNN não possui um inventor, mas um dos primeiros casos de sua aplicação é o LeNet-5 * no trabalho “ Aprendizagem baseada em gradiente aplicada ao reconhecimento de documentos” de I. LeCun e outros autores.

A CNN mata dois coelhos com uma cajadada: não há necessidade de uma definição preliminar de filtros, e o processo de aprendizado se torna de ponta a ponta. Uma arquitetura típica da CNN consiste nas seguintes partes:

• Camadas convolucionais
• Camadas de subamostragem
• Camadas densas (totalmente conectadas)

Vamos considerar cada parte em mais detalhes.

Camadas convolucionais

A camada convolucional é o principal elemento estrutural da CNN. A camada convolucional possui um conjunto de características:
Conectividade local (esparsa) . Nas camadas densas, cada neurônio é conectado a cada neurônio da camada anterior (portanto, eles eram chamados densos). Na camada convolucional, cada neurônio está conectado a apenas uma pequena parte dos neurônios da camada anterior.


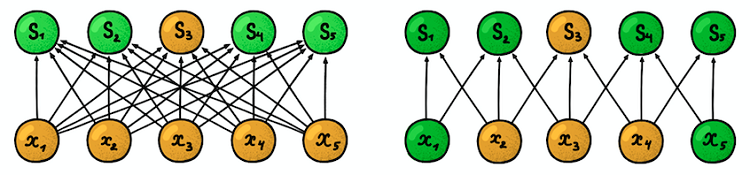Um exemplo de uma rede neural unidimensional. (esquerda) Conexão de neurônios em uma rede densa típica, (direita) Caracterização da conectividade local inerente à camada convolucional. Imagens tiradas de I. Goodfellow e outros por Deep Learning

O tamanho da área à qual o neurônio está conectado é chamado de tamanho do filtro (o comprimento do filtro no caso de dados unidimensionais, por exemplo, séries temporais ou a largura / altura no caso de dados bidimensionais, por exemplo, imagens). Na figura à direita, o tamanho do filtro é 3. Os pesos com os quais a conexão é feita são chamados de filtro (um vetor no caso de dados unidimensionais e uma matriz para dados bidimensionais). A etapa é a distância que o filtro se move sobre os dados (na figura à direita, a etapa é 1). A idéia de conectividade local nada mais é do que um kernel que avança um passo. Cada neurônio de nível convolucional representa e implementa uma posição específica do núcleo deslizando ao longo da imagem original.


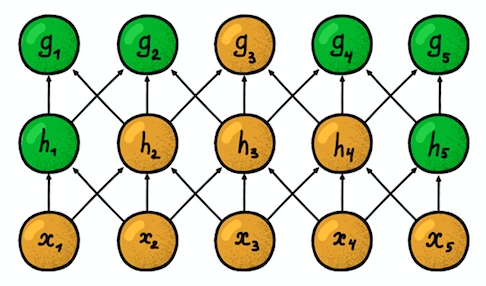Duas camadas convolucionais unidimensionais adjacentes

Outra propriedade importante é a chamada zona de suscetibilidade . Ele reflete o número de posições do sinal original que o neurônio atual pode "ver". Por exemplo, a zona de suscetibilidade da primeira camada de rede, mostrada na figura, é igual ao tamanho do filtro 3, pois cada neurônio está conectado a apenas três neurônios do sinal original. No entanto, na segunda camada, a zona de suscetibilidade já é 5, pois o neurônio da segunda camada agrega três neurônios da primeira camada, cada um dos quais com uma zona de suscetibilidade 3. Com o aumento da profundidade, a zona de suscetibilidade cresce linearmente.

Parâmetros compartilhados . Lembre-se de que no processamento clássico de imagens, o mesmo núcleo deslizou por toda a imagem. A mesma idéia se aplica aqui. Fixamos apenas o tamanho do filtro de pesos para uma camada e aplicaremos esses pesos a todos os neurônios da camada. Isso é equivalente a deslizar o mesmo núcleo por toda a imagem. Mas a questão pode surgir: como podemos aprender algo com um número tão pequeno de parâmetros?


As setas escuras representam os mesmos pesos. (esquerda) MLP regular, em que cada fator de ponderação é um parâmetro separado, (direita) Um exemplo de separação de parâmetros, em que vários fatores de ponderação indicam o mesmo parâmetro de treinamento

Estrutura espacial . A resposta a esta pergunta é simples: treinaremos vários filtros em uma camada! Eles são colocados paralelos um ao outro, formando assim uma nova dimensão.

Paramos um pouco e explicamos a ideia apresentada pelo exemplo de uma imagem RGB bidimensional de 227 × 227. Observe que aqui estamos lidando com uma imagem de entrada de três canais, o que, em essência, significa que temos três imagens de entrada ou dados de entrada tridimensionais.


A estrutura espacial da imagem de entrada

Consideraremos as dimensões dos canais como a profundidade da imagem (observe que essa não é a mesma que a profundidade das redes neurais, que é igual ao número de camadas da rede). A questão é como determinar o kernel para este caso.


Um exemplo de um núcleo bidimensional, que é essencialmente uma matriz tridimensional com uma medição de profundidade adicional. Este filtro fornece uma convolução com a imagem; ou seja, desliza sobre a imagem no espaço, calculando produtos escalares

A resposta é simples, embora ainda não seja óbvia: tornaremos o núcleo também tridimensional. As duas primeiras dimensões permanecem as mesmas (largura e altura do núcleo) e a terceira dimensão é sempre igual à profundidade dos dados de entrada.


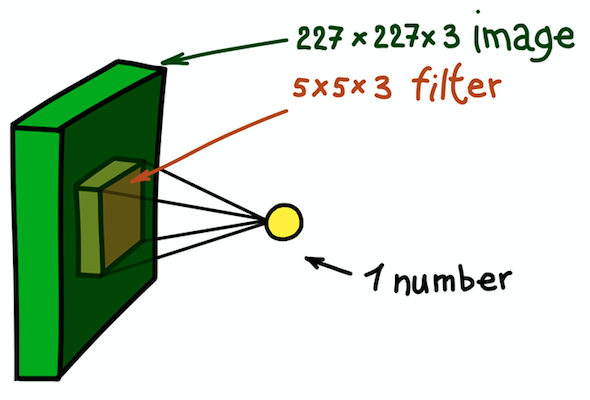Um exemplo de uma etapa de convolução espacial. O resultado do produto escalar do filtro e uma pequena parte da imagem 5 × 5 × 3 (ou seja, 5 × 5 × 5 + 1 = 76, a dimensão do produto escalar + deslocamento) é um número

Nesse caso, toda a seção 5 × 5 × 3 da imagem original é transformada em um número e a própria imagem tridimensional será transformada em um mapa de recursos ( mapa de ativação ). Um mapa de recursos é um conjunto de neurônios, cada um dos quais calcula sua própria função, levando em consideração dois princípios básicos discutidos acima: conectividade local (cada neurônio está associado a apenas uma pequena parte dos dados de entrada) e separação de parâmetros (todos os neurônios usam o mesmo filtro). Idealmente, esse mapa de recursos será o mesmo que o já encontrado no exemplo de uma rede geralmente aceita - ele armazena os resultados da convolução da imagem e filtro de entrada.


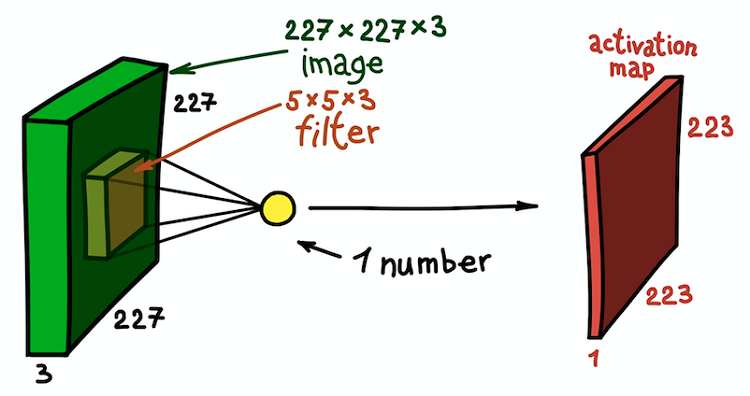Mapa de recursos como resultado da convolução do núcleo com todas as posições espaciais

Observe que a profundidade do mapa de recursos é 1, pois usamos apenas um filtro. Mas nada nos impede de usar mais filtros; por exemplo, 6. Todos eles interagirão com os mesmos dados de entrada e funcionarão independentemente um do outro. Vamos dar um passo adiante e combinar esses cartões de recursos. Suas dimensões espaciais são as mesmas, pois as dimensões dos filtros são as mesmas. Assim, os mapas de características coletados juntos podem ser considerados como uma nova matriz tridimensional, cuja dimensão de profundidade é representada por mapas de características de diferentes núcleos. Nesse sentido, os canais RGB da imagem de entrada não são outro senão os três mapas de recursos originais.


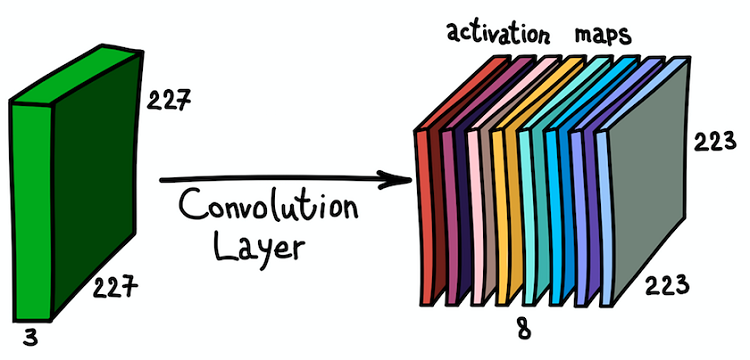A aplicação paralela de vários filtros à imagem de entrada e o conjunto resultante de cartões de ativação

Essa compreensão dos mapas de recursos e sua combinação é muito importante, pois, tendo percebido isso, podemos expandir a arquitetura da rede e instalar camadas convolucionais uma em cima da outra, aumentando a zona de suscetibilidade e enriquecendo nosso classificador.


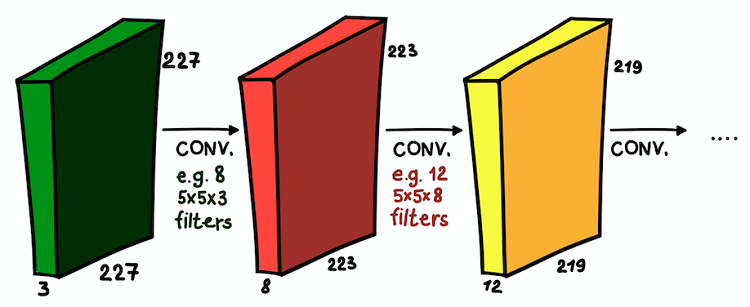Camadas convolucionais instaladas umas sobre as outras. Em cada camada, o tamanho dos filtros e seu número podem variar

Agora entendemos o que é uma rede convolucional. O objetivo principal dessas camadas é o mesmo da abordagem geralmente aceita - detectar sinais significativos da imagem. E, se na primeira camada esses sinais puderem ser muito simples (a presença de linhas verticais / horizontais), a profundidade da rede aumentará o grau de sua abstração (a presença de um cachorro / gato / pessoa).

Camadas de subamostragem

As camadas convolucionais são o principal componente da CNN. Mas há outra parte importante e frequentemente usada - são camadas de subamostras. No processamento de imagem convencional, não há analógico direto, mas uma subamostra pode ser considerada como outro tipo de kernel. O que é isso?


Exemplos de subamostragem. (esquerda) Como uma subamostra altera os tamanhos espaciais (mas não os canais!) das matrizes de dados, (direita) Um esquema básico de como uma subamostra funciona

Uma subamostra filtra uma parte da vizinhança de cada pixel dos dados de entrada com uma função de agregação específica, por exemplo, máxima, média etc. A subamostra é essencialmente a mesma que convolução, mas a função de combinação de pixels não se limita ao produto escalar. Outra diferença importante é que a subamostragem funciona apenas na dimensão espacial. Uma característica da camada de subamostragem é que o tom geralmente é igual ao tamanho do filtro (o valor típico é 2).

Uma subamostra tem três objetivos principais:

• Diminuição da dimensão espacial ou subamostragem. Isso é feito para reduzir o número de parâmetros.
• O crescimento da zona de suscetibilidade. Devido aos neurônios da subamostra nas camadas subseqüentes, mais etapas do sinal de entrada são acumuladas
• Invariância translacional a pequenas heterogeneidades na posição dos padrões no sinal de entrada. Ao calcular estatísticas de agregação de pequenas vizinhanças do sinal de entrada, uma subamostra pode ignorar pequenos deslocamentos espaciais nele.

Camadas espessas

Camadas convolucionais e subamostras servem ao mesmo objetivo - gerando atributos de imagem. A etapa final é classificar a imagem de entrada com base nos recursos detectados. Na CNN, camadas densas na parte superior da rede fazem isso. Essa parte da rede é chamada de classificação . Ele pode conter várias camadas umas sobre as outras com conectividade completa, mas geralmente termina com uma camada de classe softmax ativada por uma função de ativação logística multivariável , na qual o número de blocos é igual ao número de classes. Na saída dessa camada está a distribuição de probabilidade por classe para o objeto de entrada. Agora a imagem pode ser classificada escolhendo a classe mais provável.