"Mas nós fazemos foguetes!"

Em um artigo anterior, verifiquei se é possível ajustar automaticamente um controlador difuso usando "métodos padrão" de otimização. Acabou sendo possível e o resultado da sintonização automática é bastante satisfatório. Pelo menos para o foguete cujo modelo foi usado.

Para objetos de controle não estacionários em que os parâmetros do objeto variam em amplas faixas, um controlador difuso pode não fornecer qualidade de controle suficiente em todas as faixas de operação. Nesse caso, é necessário usar um controlador fuzzy com “sintonia multicanal”.

Vamos verificar se é possível configurar esse regulador usando métodos de otimização padrão.
Considere a síntese de um controlador difuso com sintonia multicanal para estabilizar um míssil balístico no ângulo de inclinação. Conforme solicitado nos comentários, o míssil será FAU-2. Usamos um exemplo do mesmo livro de V. Gostev. "Reguladores difusos em sistemas de controle automático".

Todos os termos usados ​​neste texto são retirados deste livro e podem não corresponder à terminologia estrita da teoria do controle automático.

Declaração do problema

Um míssil balístico que utiliza um grande número de sistemas de controle local é um objeto de controle substancialmente não estacionário. As funções de transferência, que descrevem o foguete como um objeto de controle, diferem das funções de transferência de aeronaves aladas, pois possuem links instáveis; portanto, o movimento de um foguete não controlado ao longo de um caminho programado seria instável.

Abaixo, consideramos o sistema de estabilização de um míssil balístico em ângulo de inclinação (canal de movimento longitudinal). O sistema consiste nos seguintes elementos funcionalmente necessários:
um elemento de comparação (um giroscópio livre com um sensor potenciométrico caracterizado por coeficientes de Kp);
amplificador de potência Ku e caixa de direção hidráulica.

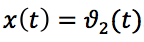
Tomando o ângulo de inclinação como coordenada de saída do foguete , para a coordenada de entrada - ângulo de direção , definimos a função de transferência no formato:


(O equipamento de direção analógico e o foguete estão incluídos no objeto de controle) Os parâmetros da função de transferência serão polinômios dependentes do tempo. Matematicamente, eles podem ser determinados por polinômios:











A tarefa assume que o horário de início do voo é de 6 segundos. Os valores polinomiais são aceitos com um turno de 6 segundos.
O modelo matemático do elo oscilatório não estacionário é descrito pela equação diferencial:



O modelo matemático de um link forçado instável é descrito pela equação diferencial:



O erro de incompatibilidade na entrada do controlador fuzzy é a diferença entre o ajuste e o ângulo de inclinação exigido.

O diagrama estrutural do modelo é mostrado na Figura 1. Para entender o princípio de formação do modelo, as linhas de comunicação indicam as variáveis X1, X e suas derivadas ( X1 '', X1 '', X ' ) de acordo com as equações dos links. O retângulo verde indica a parte do circuito do modelo correspondente ao elo oscilante, e o amarelo é o elo de força.

Os parâmetros a (t), b (t), c (t), r (t) são definidos na forma de fatores de amplificação, em blocos do tipo "amplificador". Parâmetro é definido no ganho do link de integração.


Figura 1. Diagrama estrutural do modelo.

Caminho do software, dado o ângulo de inclinação u (t) = 1 + 0,5sin (πt / 30).
Os gráficos das mudanças nos parâmetros dos foguetes durante o vôo são apresentados na Figura 2.
O valor de t = 6 é considerado o início do voo; na função polinomial, o valor (tempo + 6) é usado para calcular os parâmetros, em que tempo é o tempo de simulação atual.


Figura 2. Gráficos de mudanças nos parâmetros do foguete.

Controlador lógico difuso

Como um controlador baseado na lógica fuzzy, usamos o controlador mostrado na Figura 3. Uma incompatibilidade entre o ângulo de inclinação especificado e o ângulo real de inclinação do míssil é aplicada à entrada.

O atraso do bloco por etapa de quantização fornece uma discretização da conversão de um sinal contínuo em um sinal discreto com uma etapa de amostragem de 0,01 s.

Usando mais dois atrasos, o primeiro e o segundo desvios da derivada são calculados pelos métodos de diferença na etapa de discretização.

As unidades de fase calculam os valores dos termos de desvio, taxa de mudança e aceleração. (Para mais informações, consulte o texto anterior ). Na saída de cada bloco de fases, obtemos um vetor de termos para variáveis ​​linguísticas. (ver tabela 1)

Variável linguística	Termos
Desvio	Mais Norma Menos
Taxa de variação	Está crescendo Não muda Está caindo
Mudança mais rápida	Está aumentando Constante Diminui

Os blocos do desmultiplexador analisam os vetores em termos separados, que são transmitidos aos blocos de processamento lógico de acordo com as regras de inferência fuzzy.
O resultado da inferência difusa também possui três variáveis ​​linguísticas: “reduzir”, “não mudar”, “aumentar”. As seguintes regras de inferência são escritas na forma de um diagrama.

• Se Mais e Crescimento e taxa de crescimento aumentar => diminuir .
• Se a norma , e não muda e é constante => nós não mudamos .
• Se Menos e Quedas e a taxa de queda aumentar => aumentar .

Figura 3. Esquema de um regulador baseado em lógica nebulosa.

Na desnazificação, funções triangulares com uma base comum são usadas como uma função de associação (ver Fig. 4)

Figura 4. Funções de fases triangulares com uma base comum.

Supõe-se que as funções sejam simétricas em relação a 0, neste caso, para descrever três funções triangulares, um valor de Max é suficiente. Para os mostrados na figura, Max = 30.

As mesmas funções de associação são usadas para saída.

Para uma definição completa do regulador, é necessário definir os valores máximos para os blocos de variáveis ​​de fase:

- deltaMax - desvio máximo;
- divMax - a derivada máxima do desvio;
- div2Max - segunda derivada máxima do desvio;
- uMax - ação máxima de controle.

Otimização total do processo

A ação máxima de controle é executada igual ao uMax - 70.
Assim, resta escolher três parâmetros para a função de mudança de fase.
Nesse problema, a incompatibilidade é alimentada por uma etapa no momento zero do tempo do modelo, u (t) = 1 + 0,5.sin (πt / 30).

A trajetória programada, o determinado ângulo de inclinação u (t) = 1 + 0,5sin (πt / 30), causa um efeito passo a passo no primeiro segundo do processo de transição, como resultou durante experimentos com a tarefa anterior, os controladores sintonizados em um processo de controle suave, com ação passo a passo, podem não forneça a qualidade exigida do processo de transição.

Portanto, para otimização, formamos três critérios:

1. Tempo transitório - precisamos chegar a um determinado caminho do programa o mais rápido possível.
2. Desvio padrão.
3. Número de comutações - em experimentos com a tarefa anterior, tivemos a opção quando houve oscilações de alta frequência da ação de controle na saída do sistema de controle.

O esquema geral do bloco de otimização é mostrado na Figura 5.

Figura 5. Esquema do bloco de otimização.

Parâmetros de entrada do bloco de otimização:

- desvio do ângulo de inclinação fornecido.
- impacto regulatório.

Para calcular o tempo transitório, é utilizado um comutador no qual o tempo atual do modelo é aplicado a uma das entradas. Após o bloco, existe um atraso para o período de quantização, o valor do atraso é transmitido para a segunda entrada.

Como um comutador, um módulo de desvio é usado. Se o módulo de desvio for maior que o valor de comutação definido (0,02), o tempo atual será emitido no bloco; se o módulo for menor que o valor definido, o tempo armazenado quando o desvio foi maior será transmitido para a saída. Se ainda mais o desvio exceder o limite, obteremos novamente o tempo. Assim, na saída, sempre temos a última vez em que o desvio excedeu o valor definido.
Como unidade de comutação, o sinal da ação de controle é alterado de + para -. Para calcular o número de comutações, usamos o bloco "impulso ao longo da frente" que, quando a entrada é alterada de 0 para 1, fornece um pulso de duração na etapa de integração, os impulsos são calculados pelo integrador. Na saída do bloco - o número de comutações.

- O bloco de otimização seleciona os valores dos parâmetros a serem otimizados de forma a minimizar os três parâmetros:
- deltaMax - desvio máximo;
- divMax - a derivada máxima do desvio;
- div2Max - a segunda derivada máxima do desvio.

O resultado é a otimização do processo completo de transição.

Iniciando o processo de otimização, obtivemos os seguintes parâmetros ótimos para o controlador fuzzy:

- deltaMax = 0,185 - desvio máximo;
- divMax = 0,278 - a derivada máxima do desvio;
- div2Max = 1,291 - a segunda derivada máxima do desvio.

Os resultados do processo otimizado são mostrados na Figura 6.

Figura 6a. O processo de transição.

Figura 6b. Opções de controle.

Pode-se observar que a otimização, em geral, foi um sucesso, mas os desvios do ângulo de inclinação determinado existem quase ao longo do processo. O gráfico de desvio ampliado mostra que os desvios após a otimização e a conclusão do processo de transição estão na faixa de 0,015 a 0,02. (ver fig. 7)

Figura 7. Desvio no processo de controle.

Otimização por seções de voo.

Vamos tentar melhorar o processo selecionando os parâmetros do controlador fuzzy para diferentes seções do voo do foguete.

A primeira seção é a hora do início até a saída em um determinado caminho. Com base no gráfico de desvio, o processo de transição associado ao efeito stepwise inicial termina em 20 segundos. (veja a fig. 7). Nesta seção, a otimização do tempo do processo de transição ocorre.

Defina o horário final do cálculo para 20 segundos. E realizaremos a otimização, removendo o desvio padrão dos critérios. Vamos otimizar no momento do processo de transição e no número de trocas. O diagrama de blocos de otimização é mostrado na Figura 8.


Figura 8. Esquema de otimização na primeira fase do voo.

A otimização automática para a primeira fase do vôo por até 20 segundos produziu os seguintes parâmetros para a regulação difusa:

- deltaMax = 0,056 - desvio máximo;
- divMax = 0,0968 - a derivada máxima do desvio;
- div2Max = 0.987 - a segunda derivada máxima do desvio.

O processo de transição após a otimização é mostrado na Figura 9.

Desvios em uma escala maior são mostrados na Figura 10.

Figura 9a. O processo de transição.

Figura 9b. Opções de controle.

Figura 10. Desvio de escala maior da primeira perna do voo.

Os gráficos mostram que a superação diminuiu e o desvio após o final do processo de transição se tornou menor que 0,005.

Para otimização na próxima seção de vôo, realizaremos a simulação com o estado salvo obtido na primeira seção.

A simulação ocorre de 20 a 40 segundos do voo do míssil balístico, a otimização ocorre ao longo do processo.

Como concluímos o processo de transição no início da segunda seção, realizamos a otimização apenas pelo desvio e pelo número de comutadores. O diagrama de blocos de otimização é mostrado na Figura 11.


Figura 11. Esquema de otimização para a segunda seção de voo.

A otimização automática para a segunda fase do vôo de 20 a 40 segundos produziu os seguintes parâmetros para a regulação difusa:

- deltaMax = 0,056 - desvio máximo;
- divMax = 0,0974 - a derivada máxima do desvio;
- div2Max = 0,980 - a segunda derivada máxima do desvio.

Com os parâmetros fornecidos, o desvio do ângulo de inclinação em relação ao determinado diminui durante toda a segunda seção de tempo do voo. Mas se usarmos os parâmetros obtidos por otimização na segunda parte do vôo para controlar até 66 segundos, pode-se ver que a precisão começa a diminuir e o desvio começa a aumentar após 40 segundos (veja a Fig. 12).


Figura 12. Processo de controle de mísseis balísticos com configurações otimizadas para vôo de 20 a 40 segundos.

Repita a otimização para a terceira perna do voo. Salve os resultados por 40 segundos.

Nós os usamos para iniciar e otimizar em uma seção de 40 a 66 segundos.

A otimização automática para a última seção de vôo, de 40 a 66 segundos, produziu os seguintes parâmetros para a regulação difusa:

- deltaMax = 0,0146 - desvio máximo;
- divMax = 0,0157 - a derivada máxima do desvio;
- div2Max = 0,555 - a segunda derivada máxima do desvio.

O gráfico do processo de controle na última seção do vôo de míssil balístico após a otimização é mostrado na Figura 13.

Figura 13. Processo de controle de mísseis balísticos na última etapa do vôo.

A Figura 13 mostra que, com as novas configurações, o desvio no intervalo de tempo de vôo de 40 a 66 segundos não aumenta, em contraste com as configurações otimizadas para o segundo segmento de vôo (consulte a Fig. 12).

Assim, obtivemos as configurações do controlador difuso para três seções do voo. Vamos criar uma chave de modo que alterará as configurações do controlador durante o voo. O circuito da chave de modo é mostrado na Figura 14.


Figura 14. Interruptor de modo do controlador de mísseis balísticos difusos.

Os modos de comutação ocorrerão no tempo; na parte superior, um circuito lógico simples compara o tempo atual do modelo com os pontos de comutação. Como resultado, um vetor de controle de três valores é formado no multiplexador. Nesse vetor, o valor 1 está na posição do intervalo de tempo atual.

Os parâmetros do controlador difuso calculados anteriormente pelos métodos de otimização são agrupados em vetores de três valores.

Com a ajuda de um bloco de amostragem de três valores, é selecionado um que corresponde a 1. No vetor de controle, portanto, quando o tempo muda, os parâmetros transferidos para o controlador difuso mudam de acordo com a seção de vôo atual.

Para maior clareza, os valores transmitidos pela linha de comunicação são exibidos no diagrama. A figura corresponde à última seção de um vôo de míssil balístico. O tempo é superior a 40 segundos. O vetor de controle (0, 0, 1), o último parâmetro do conjunto, é fornecido ao controlador.

O resultado da simulação do controle do ângulo de inclinação do foguete com a troca dos parâmetros do regulador é mostrado na Figura 15.

Figura 15a. O processo de transição.

Figura 15b. Opções de controle.

Conclusões:
Um controlador baseado na lógica fuzzy pode ser configurado pelo método de otimização para funcionar no modo de comutação de parâmetros.

O desvio ao trabalhar com parâmetros variáveis ​​no exemplo dado diminuiu 3-5 vezes em comparação com a operação do controlador com parâmetros constantes.

Arquivo com projetos para estudo independente pode ser baixado aqui ...