A essência geral das classificações de inserção é a seguinte:
- Repete os elementos na parte não classificada da matriz.
- Cada elemento é inserido na parte classificada da matriz no local em que deveria estar.
Isso, em princípio, é tudo o que você precisa saber sobre a classificação por inserções. Ou seja, as classificações de inserção sempre dividem a matriz em 2 partes - classificadas e não classificadas. Qualquer item é recuperado da peça não classificada. Como a outra parte da matriz é classificada, você pode encontrar rapidamente seu lugar nessa matriz para esse elemento extraído. O elemento é inserido quando necessário, como resultado da parte classificada da matriz aumentar e da parte não classificada diminuir. Só isso. Todos os tipos de pastilhas funcionam de acordo com esse princípio.
O ponto mais fraco dessa abordagem é inserir um elemento na parte classificada da matriz. Na verdade, não é fácil e quais truques você não precisa para concluir esta etapa.
Classificação de inserção simples

Percorremos a matriz da esquerda para a direita e processamos cada elemento por vez. À esquerda do próximo elemento, aumentamos a parte classificada da matriz, para a direita, à medida que o processo avança, a parte não classificada evapora lentamente. Na parte classificada da matriz, o ponto de inserção do próximo elemento é pesquisado. O próprio elemento é enviado para o buffer, como resultado de uma célula vazia aparecer na matriz - isso permite que você altere os elementos e libere o ponto de inserção.
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
Usando inserções simples como exemplo, a principal vantagem da maioria (mas não todas!) A classificação por inserções parece demonstrativa, ou seja, processamento muito rápido de matrizes quase ordenadas:

Nesse cenário, mesmo a implementação mais primitiva de inserções de classificação provavelmente ultrapassará o algoritmo super otimizado para uma classificação rápida, inclusive em matrizes grandes.
Isso é facilitado pela idéia principal dessa classe - a transferência de elementos da parte não classificada da matriz para a classificada. Com a proximidade de dados de magnitude semelhante, o ponto de inserção geralmente está localizado próximo à borda da peça classificada, o que permite a inserção com o mínimo de sobrecarga.
Não há nada melhor para lidar com matrizes quase ordenadas do que a classificação por inserção. Quando você encontra informações em algum lugar em que a melhor complexidade de tempo para classificar por inserções é
O ( n ) , provavelmente você está se referindo a situações com matrizes quase ordenadas.
Classificar por inserções simples de pesquisa binária

Como o local a ser inserido é pesquisado na parte classificada da matriz, a ideia de usar uma pesquisa binária se sugere. Outra coisa é que a busca pelo site de inserção não é crítica para a complexidade de tempo do algoritmo (o principal consumidor de recursos é o estágio de inserção do elemento na própria posição encontrada), portanto, essa otimização faz pouco.
E, no caso de uma matriz quase classificada, uma pesquisa binária pode funcionar ainda mais lentamente, pois começa no meio da seção classificada, que provavelmente estará muito longe do ponto de inserção (e serão necessárias menos etapas para executar uma pesquisa normal da posição do elemento ao ponto de inserção, se os dados na matriz como um todo ordenado).
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
Em defesa da pesquisa binária, observo que ele pode dizer a palavra final na eficácia de outras classificações por inserções. Graças a ele, em particular, algoritmos como a classificação de bibliotecários e solitários vão para a complexidade de tempo médio
O ( n log n ) . Mas sobre eles mais tarde.
Emparelhar a classificação por inserções simples
Modificação de pastilhas simples, desenvolvidas nos laboratórios secretos da Oracle Corporation. Essa classificação faz parte do JDK e faz parte do Quicksort de pivô duplo. É usado para classificar matrizes pequenas (até 47 elementos) e classificar áreas pequenas de matrizes grandes.

Não um, mas dois elementos adjacentes são enviados para o buffer de uma só vez. Primeiro, o elemento maior do par é inserido e, imediatamente após, o método de inserção simples é aplicado ao elemento menor do par.
O que isso dá? Economias para manipular um item menor de um par. Para ele, a busca pelo ponto de inserção e a própria inserção são realizadas apenas na parte classificada da matriz, que não inclui a área classificada usada para processar um elemento maior do par. Isso se torna possível porque os elementos maiores e menores são processados imediatamente um após o outro em uma passagem do loop externo.
Isso não afeta a complexidade do tempo médio (ainda permanece igual a
O ( n 2 )), no entanto, as inserções emparelhadas funcionam um pouco mais rápido que as usuais.
Ilustro os algoritmos em Python, mas aqui dou a fonte original (modificada para facilitar a leitura) em Java:
for (int k = left; ++left <= right; k = ++left) {
Classificação da Shell

Esse algoritmo tem uma abordagem muito inteligente para determinar qual parte da matriz é considerada classificada. Nas inserções simples, tudo é simples: a partir do elemento atual, tudo à esquerda já está classificado, tudo à direita ainda não está classificado. Diferentemente das inserções simples, a classificação do Shell não tenta formar imediatamente uma parte estritamente classificada da matriz à esquerda de um elemento. Ele cria uma parte
quase classificada da matriz à esquerda do elemento e o faz com rapidez suficiente.
A classificação do shell lança o elemento atual no buffer e o compara com o lado esquerdo da matriz. Se encontrar elementos maiores à esquerda, os deslocará para a direita, abrindo espaço para inserção. Mas, ao mesmo tempo, não ocupa toda a parte esquerda, mas apenas um certo grupo de elementos, onde os elementos são espaçados entre si por uma certa distância. Esse sistema permite que você insira rapidamente elementos aproximadamente na área da matriz onde eles devem estar localizados.
A cada iteração do loop principal, essa distância diminui gradualmente e, quando se torna igual a um, a classificação do Shell nesse momento se transforma em uma classificação clássica com inserções simples, que foram dadas ao processamento de uma matriz quase classificada. Uma classificação de matriz quase classificada é inserida em conversões totalmente classificadas rapidamente.
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
A classificação pente por um princípio semelhante melhora a classificação de bolhas, de modo que a complexidade de tempo do algoritmo com
O ( n 2 ) salta até
O ( n log n ) . Infelizmente, a Shell não consegue repetir esse feito - a melhor complexidade de tempo chega a
O ( n log 2 n ) .
Vários habrastati foram escritos sobre a classificação do Shell, portanto, não seremos sobrecarregados com informações e seguiremos em frente.
Classificação de árvores
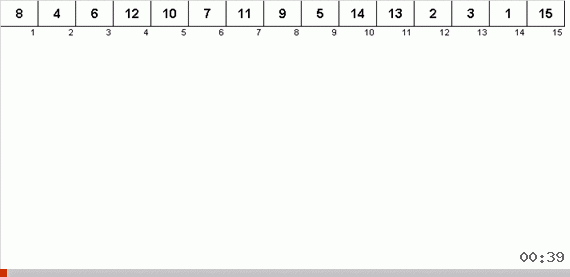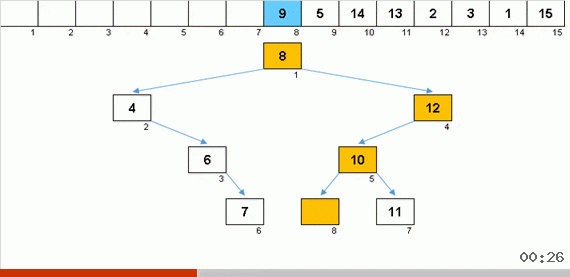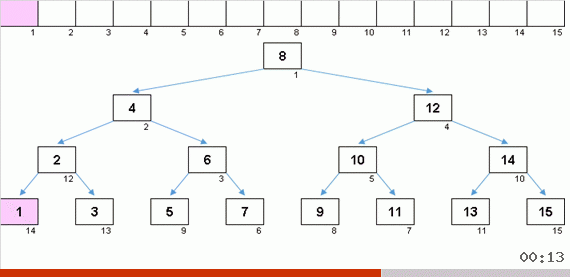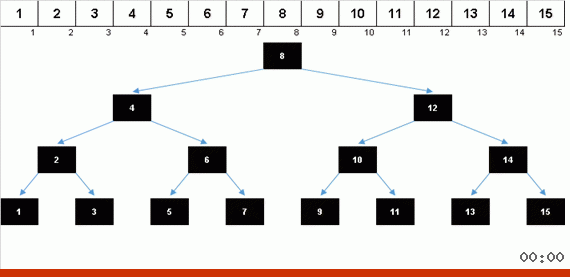
A classificação com uma árvore devido à memória adicional resolve rapidamente o problema de adicionar outro elemento à parte classificada da matriz. Além disso, a árvore binária atua como a parte classificada da matriz. Uma árvore é formada literalmente em tempo real ao iterar sobre os elementos.
O elemento é comparado primeiro com a raiz e, em seguida, com mais nós aninhados de acordo com o princípio: se o elemento for menor que o nó, desceremos o ramo esquerdo, se não menos, o direito. Uma árvore construída por essa regra pode ser facilmente contornada para passar de nós com valores mais baixos para nós com valores maiores (e, assim, obter todos os elementos em ordem crescente).
O principal problema da classificação por inserções (o custo de inserir um elemento em seu lugar na parte classificada da matriz) é resolvido aqui, a construção prossegue rapidamente. De qualquer forma, para liberar o ponto de inserção, não é necessário mover lentamente as caravanas de elementos como nos algoritmos anteriores. Parece que aqui está, o melhor dos insertos de classificação. Mas há um problema.
Quando você obtém uma bela árvore de Natal simétrica (a chamada árvore perfeitamente equilibrada), como na animação três parágrafos acima, a inserção ocorre rapidamente, porque a árvore neste caso tem os níveis de aninhamento mais baixos possíveis. Mas uma estrutura equilibrada (ou pelo menos próxima a isso) de uma matriz aleatória raramente é obtida. E a árvore, provavelmente, será imperfeita e desequilibrada - com distorções, um horizonte desarrumado e um número excessivo de níveis.
Uma matriz aleatória com valores de 1 a 10. Os elementos nessa ordem geram uma árvore binária desequilibrada: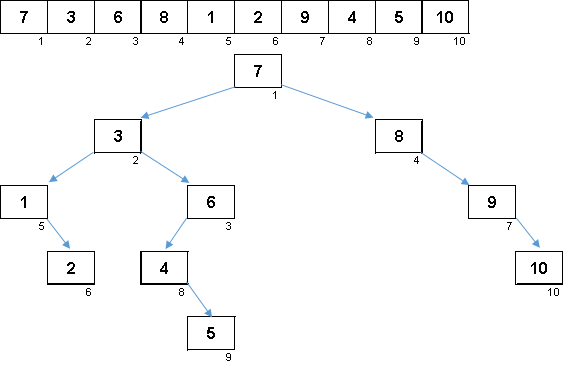
Uma árvore não é suficiente para construir, ainda precisa ser contornada. Quanto mais desequilíbrio - mais forte o algoritmo de deslocamento da árvore escorregará. Aqui, como dizem as estrelas, uma matriz aleatória pode gerar um obstáculo feio (o que é mais provável) e um fractal semelhante a uma árvore.
Os valores dos elementos são os mesmos, mas a ordem é diferente. Uma árvore binária balanceada é gerada: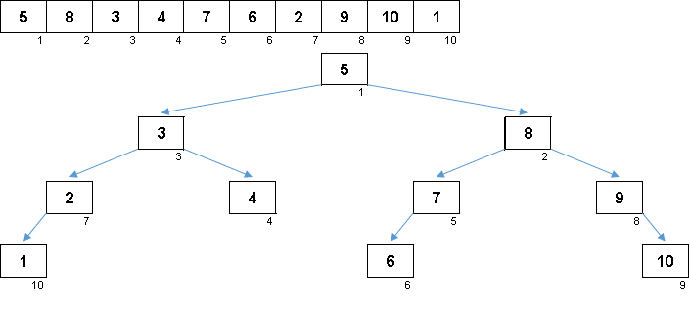
 Na bela sakura
Na bela sakura
Pétala insuficiente:
Uma árvore binária de dezenas.O problema das árvores desequilibradas é resolvido pela classificação por inversão, que usa um tipo especial de árvore de pesquisa binária - árvore de exibição. Esta é uma maravilhosa árvore de transformadores, que após cada operação é reconstruída em um estado equilibrado. Sobre isso será um artigo separado. Nesse momento, prepararei implementações do Python para as classificações Tree Sort e Splay.
Bem, nós analisamos brevemente as inserções de classificação mais populares. Pastilhas simples, casca e árvore binária que todos conhecemos da escola. Agora considere outros representantes desta classe, não tão amplamente conhecidos.
Wiki / Wiki -
Inserção , Shell / Shell , Árvore / ÁrvoreArtigos da série:
Quem usa o AlgoLab - eu recomendo atualizar o arquivo. Adicionei inserções simples de pesquisa binária e inserções emparelhadas a este aplicativo. Ele também reescreveu completamente a visualização do Shell (na versão anterior, não havia nada para entender) e acrescentou destaque ao ramo pai ao inserir um elemento na árvore binária.