Redes neurais, princípios fundamentais de operação, diversidade e topologia

As redes neurais revolucionaram o campo do reconhecimento de padrões, mas devido à interpretabilidade não óbvia do princípio de operação, elas não são usadas em áreas como medicina e avaliação de riscos. Requer uma representação visual da rede, o que a tornará não uma caixa preta, mas pelo menos "translúcida". Cristopher Olah, em Redes Neurais, Distribuidores e Topologia, demonstrou os princípios da operação de redes neurais e os conectou à teoria matemática da topologia e diversidade, que serviu de base para este artigo. Para demonstrar a operação de uma rede neural, são usadas redes neurais profundas de baixa dimensão.

Compreender o comportamento de redes neurais profundas geralmente não é uma tarefa trivial. É mais fácil explorar redes neurais profundas de baixa dimensão - redes nas quais existem apenas alguns neurônios em cada camada. Para redes de baixa dimensão, você pode criar visualizações para entender o comportamento e o treinamento dessas redes. Essa perspectiva fornecerá uma compreensão mais profunda do comportamento das redes neurais e observará a conexão que combina redes neurais com um campo de matemática chamado topologia.

Uma série de coisas interessantes segue-se a isso, incluindo os limites inferiores fundamentais da complexidade de uma rede neural capaz de classificar determinados conjuntos de dados.

Considere o princípio da rede usando um exemplo

Vamos começar com um conjunto de dados simples - duas curvas em um avião. A tarefa de rede aprenderá a classificar os pontos pertencentes às curvas.



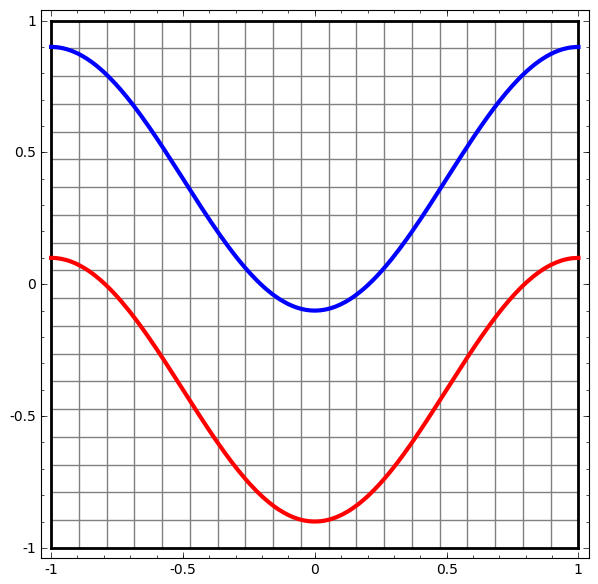
Uma maneira óbvia de visualizar o comportamento de uma rede neural, para ver como o algoritmo classifica todos os objetos possíveis (em nosso exemplo, pontos) de um conjunto de dados.

Vamos começar com a classe mais simples de rede neural, com uma camada de entrada e saída. Essa rede tenta separar duas classes de dados, dividindo-os por uma linha.



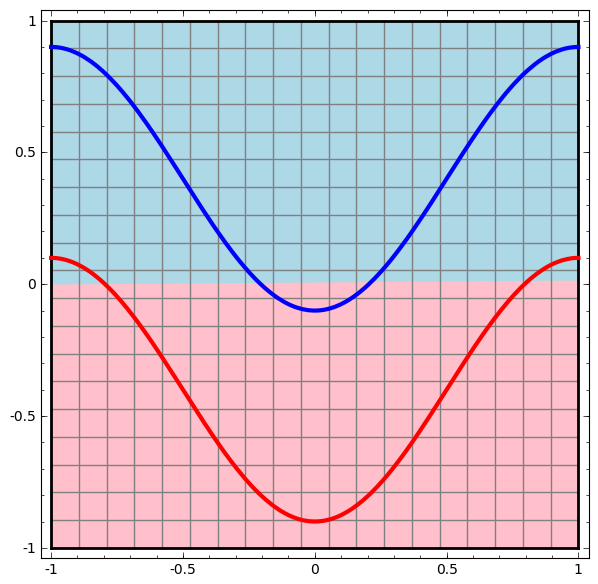
Essa rede não é usada na prática. As redes neurais modernas geralmente têm várias camadas entre sua entrada e saída, chamadas camadas "ocultas".

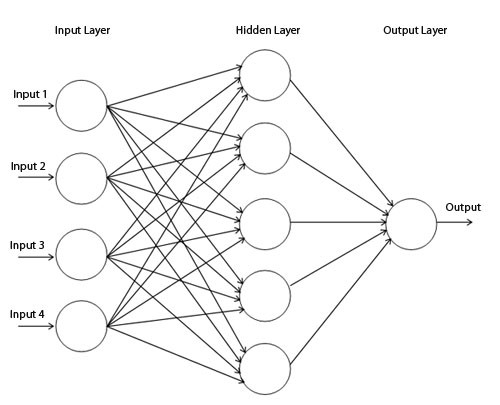
Diagrama de rede simples

Visualizamos o comportamento dessa rede, observando o que ela faz com diferentes pontos em seu campo. Uma rede de camada oculta separa os dados de uma curva mais complexa do que uma linha.



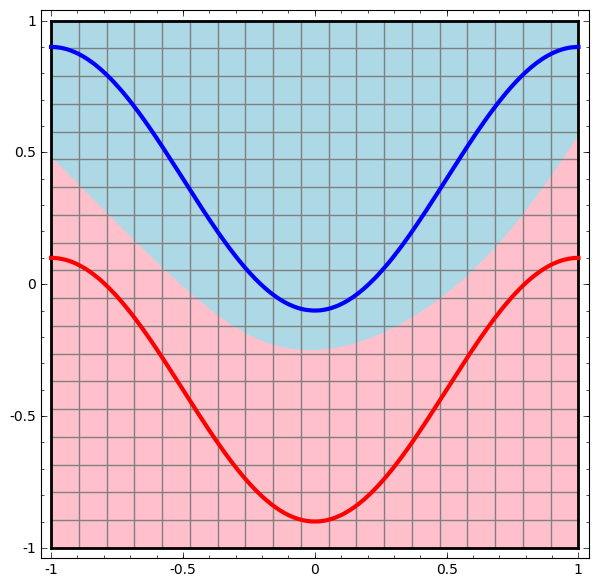
Com cada camada, a rede transforma os dados, criando uma nova visualização. Podemos ver os dados em cada uma dessas visualizações e como a rede com uma camada oculta os classifica. Quando o algoritmo atinge a apresentação final, a rede neural desenha uma linha através dos dados (ou em dimensões superiores - um hiperplano).

Na visualização anterior, os dados em uma visualização bruta são considerados. Você pode imaginar isso olhando para a camada de entrada. Agora, considere-o depois de convertido para a primeira camada. Você pode imaginar isso olhando para a camada oculta.
Cada medida corresponde à ativação de um neurônio na camada.



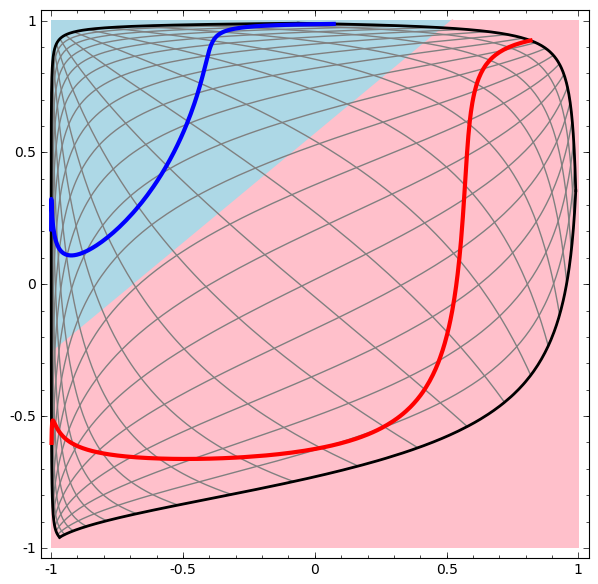
A camada oculta é treinada na visualização para que os dados sejam separáveis ​​linearmente.

Renderização de camada contínua

Na abordagem descrita na seção anterior, aprendemos a entender redes observando a apresentação correspondente a cada camada. Isso nos dá uma lista discreta de visualizações.

A parte não trivial é entender como passamos de um para o outro. Felizmente, os níveis de redes neurais têm propriedades que tornam isso possível.
Existem muitos tipos diferentes de camadas usadas em redes neurais.

Considere uma camada tanh para um exemplo específico. A camada tanh-tanh (Wx + b) consiste em:

1. A transformação linear da matriz "peso" W
2. Tradução usando o vetor b
3. Aplicação local de tanh.

Podemos representar isso como uma transformação contínua da seguinte maneira:



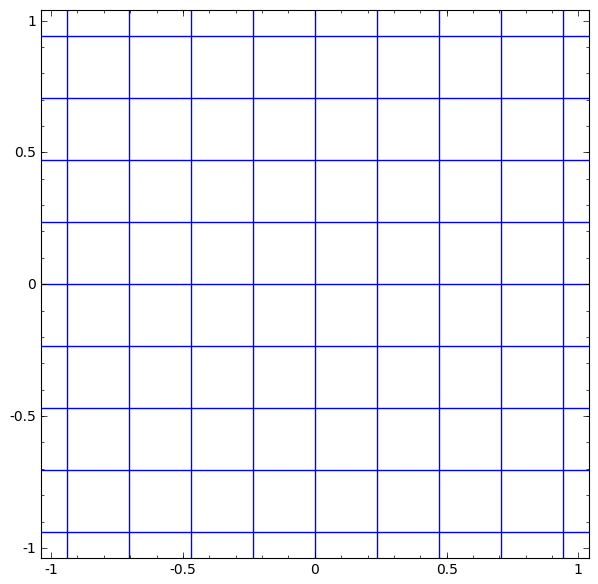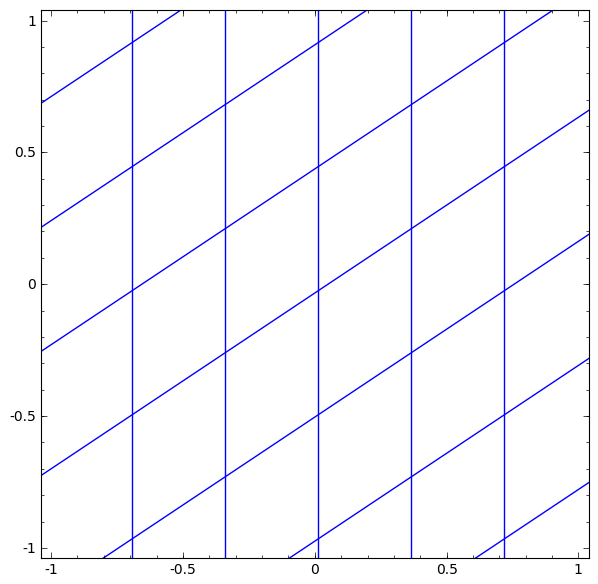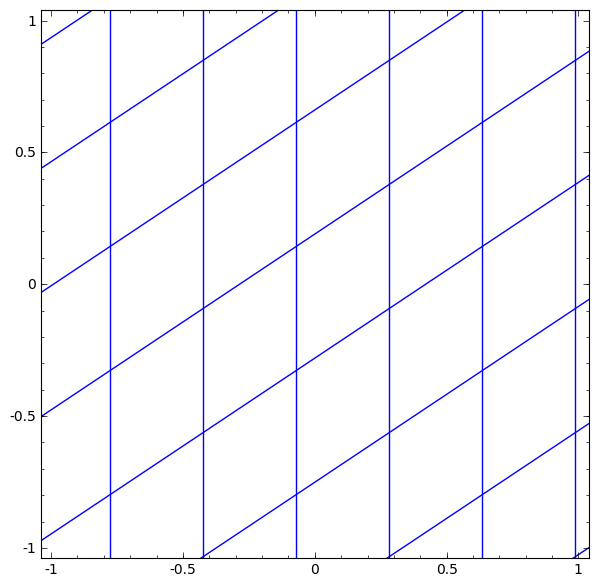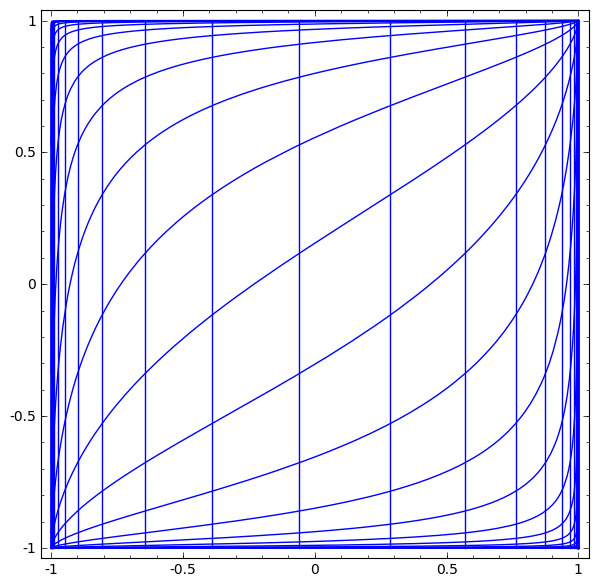
Este princípio de operação é muito semelhante a outras camadas padrão que consistem em uma transformação afim, seguida pela aplicação pontual de uma função de ativação monotônica.
Este método pode ser usado para entender redes mais complexas. Portanto, a rede a seguir classifica duas espirais levemente emaranhadas usando quatro camadas ocultas. Com o tempo, pode-se observar que a rede neural passa de uma visão bruta para um nível superior que a rede estudou para classificar dados. Enquanto as espirais são inicialmente emaranhadas, no final elas são linearmente separáveis.



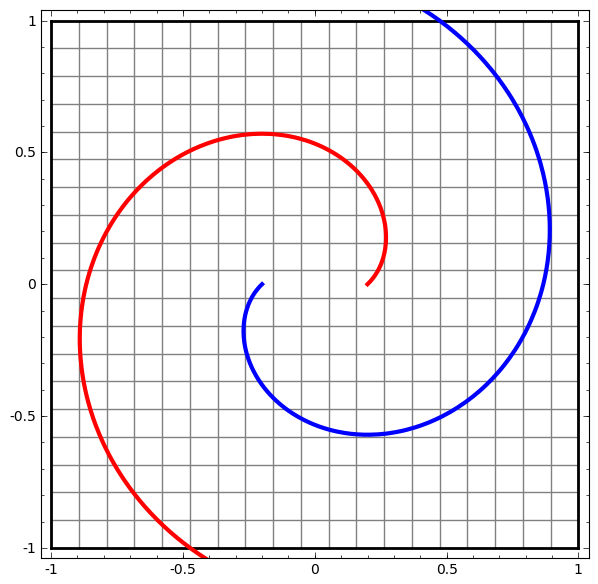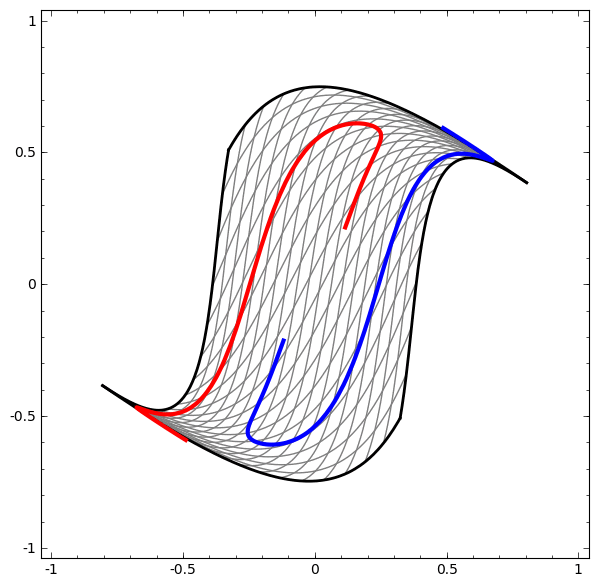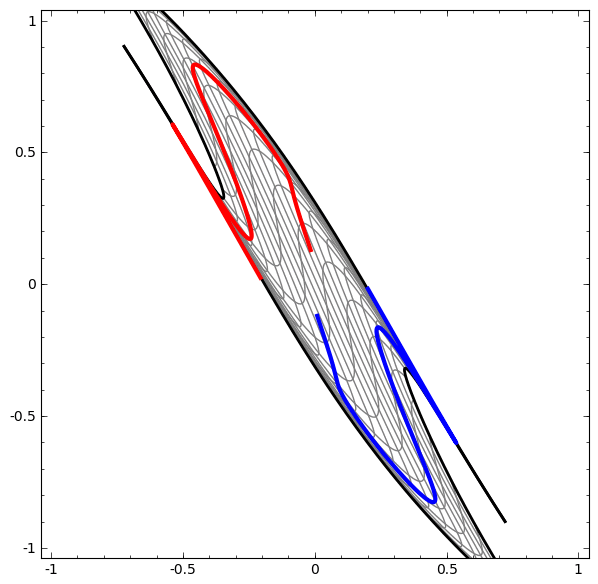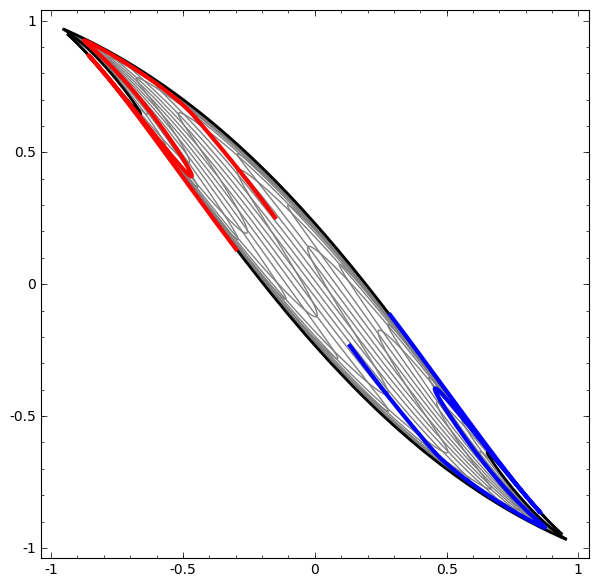
Por outro lado, a próxima rede, que também usa vários níveis, mas não pode classificar duas espirais, que são mais emaranhadas.



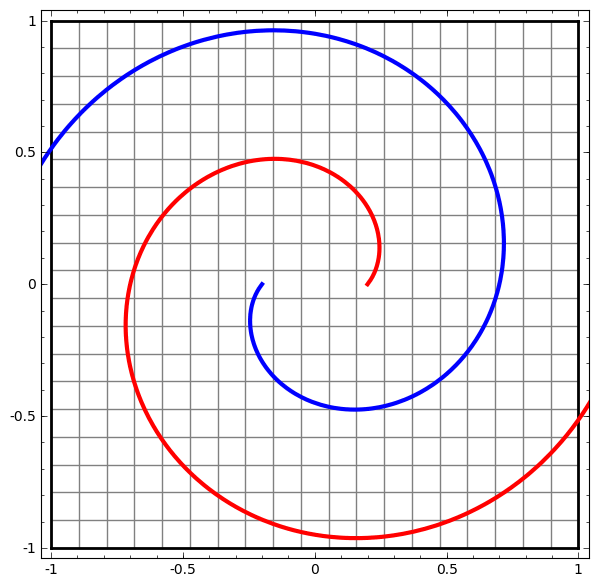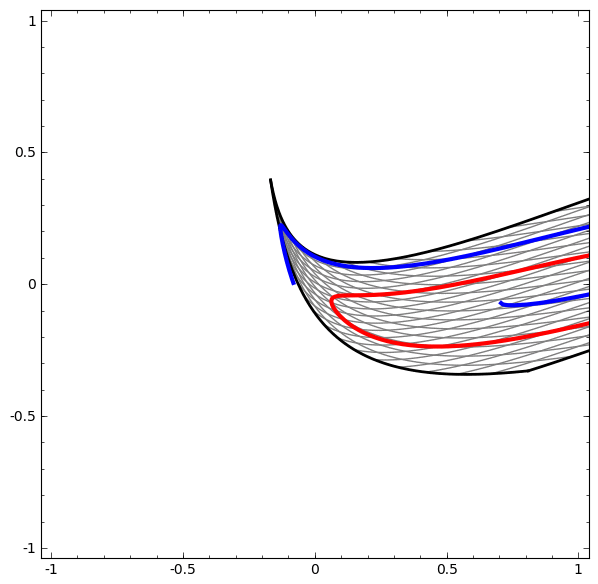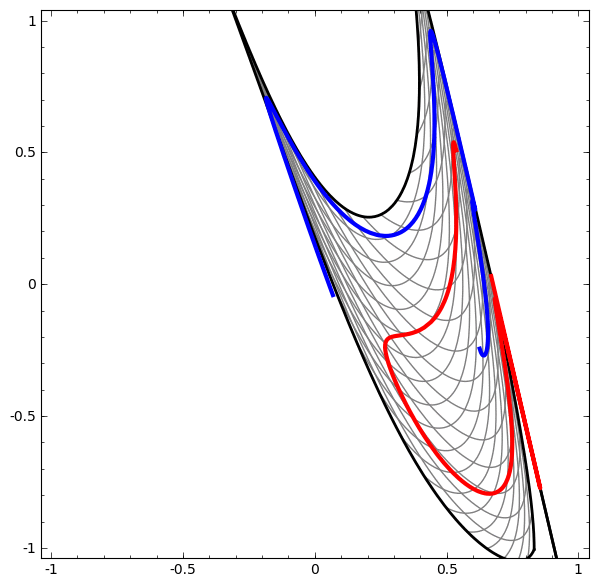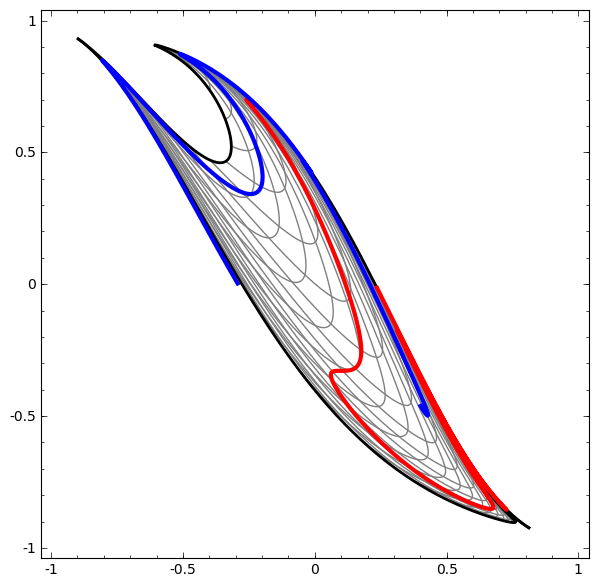
Deve-se notar que essas tarefas têm complexidade limitada, porque redes neurais de baixa dimensão são usadas. Se redes mais amplas fossem usadas, a solução de problemas seria simplificada.

Camadas de Tang

Cada camada estica e comprime o espaço, mas nunca corta, não quebra e não dobra. Intuitivamente, vemos que as propriedades topológicas são preservadas em cada camada.

Tais transformações que não afetam a topologia são chamadas homomorfismos (Wiki - Este é um mapeamento do sistema algébrico A que preserva as operações básicas e as relações básicas). Formalmente, são bijections que são funções contínuas em ambas as direções. Em um mapeamento bijetivo, cada elemento de um conjunto corresponde exatamente a um elemento de outro conjunto, e um mapeamento inverso que possui a mesma propriedade é definido.

O teorema

Camadas com N entradas e saídas N são homomorfismos se a matriz de pesos W não for degenerada. (Você precisa ter cuidado com o domínio e o alcance.)

Topologia e classificação

Considere um conjunto de dados bidimensional com duas classes A, B⊂R2:

A = {x | d (x, 0) <1/3}

B = {x | 2/3 <d (x, 0) <1}



A vermelho, B azul

Requisito: Uma rede neural não pode classificar esse conjunto de dados sem 3 ou mais camadas ocultas, independentemente da largura.

Como mencionado anteriormente, a classificação com uma função sigmóide ou camada softmax é equivalente a tentar encontrar o hiperplano (ou, nesse caso, a linha) que separa A e B na representação final. Com apenas duas camadas ocultas, a rede é topologicamente incapaz de compartilhar dados dessa maneira e está fadada ao fracasso nesse conjunto de dados.
Na próxima visualização, observamos uma visualização latente enquanto a rede está treinando junto com a linha de classificação.



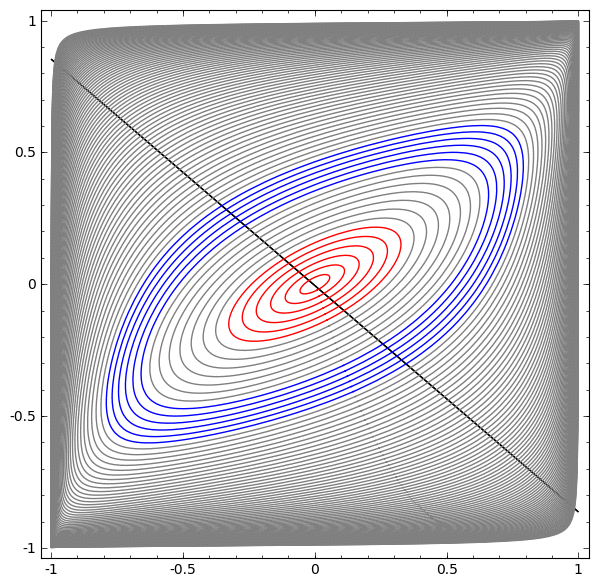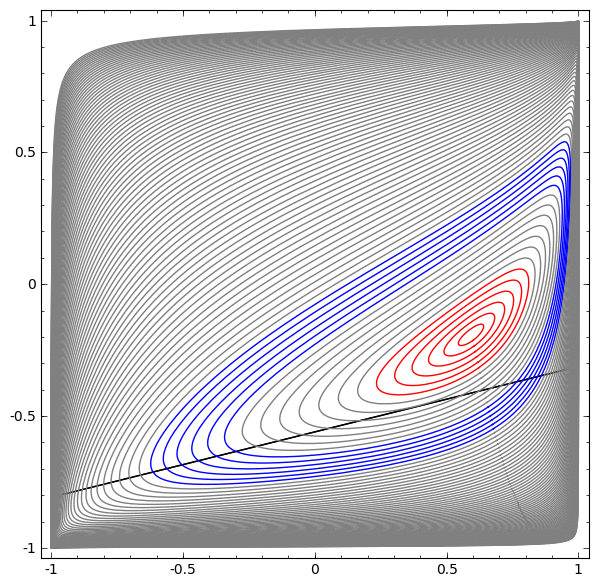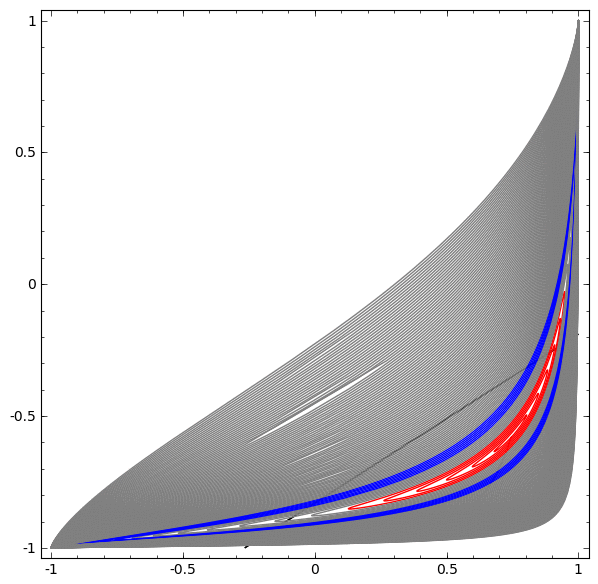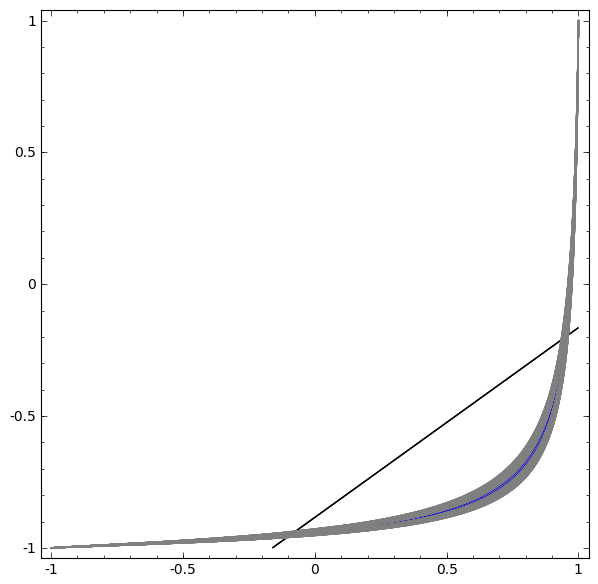
Para essa rede de treinamento, não basta atingir um resultado de cem por cento.
O algoritmo cai para um mínimo local não produtivo, mas é capaz de atingir ~ 80% de precisão na classificação.

Neste exemplo, havia apenas uma camada oculta, mas não funcionou.
Declaração. Cada camada é um homomorfismo ou a matriz de peso da camada tem um determinante 0.


Se adicionarmos um terceiro elemento oculto, o problema se tornará trivial. A rede neural reconhece a seguinte representação:



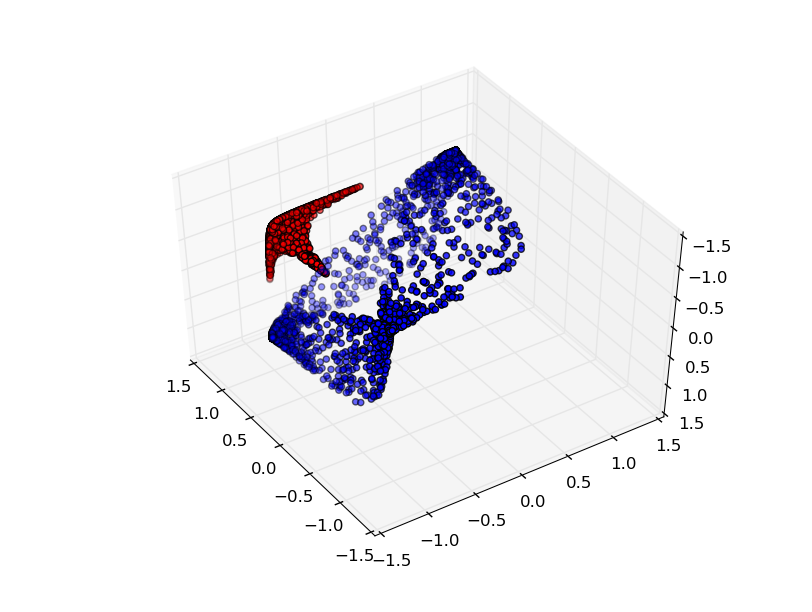
A visualização torna possível separar conjuntos de dados com um hiperplano.
Para entender melhor o que está acontecendo, vejamos um conjunto de dados ainda mais simples, unidimensional:



A = [- 1/3,1 / 3]
B = [- 1, −2 / 3] ∪ [2 / 3,1]
Sem usar uma camada de dois ou mais elementos ocultos, não podemos classificar esse conjunto de dados. Mas, se usarmos uma rede com dois elementos, aprenderemos como representar os dados como uma boa curva que nos permite separar classes usando uma linha:



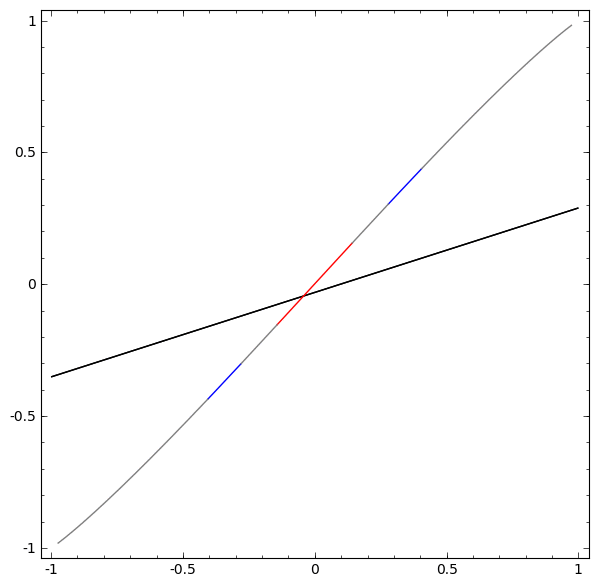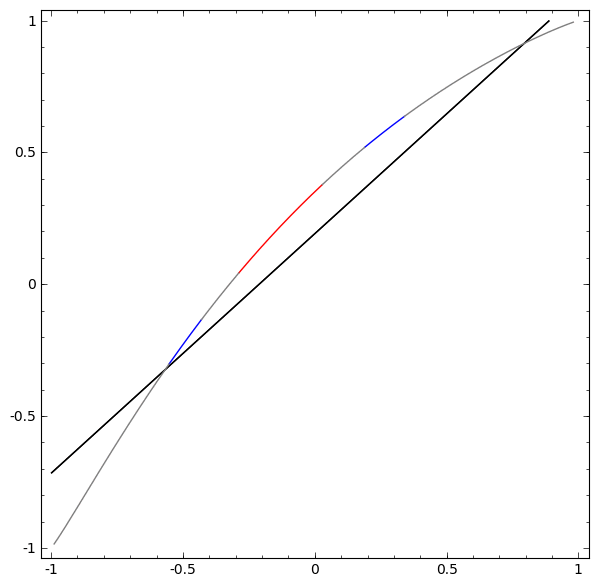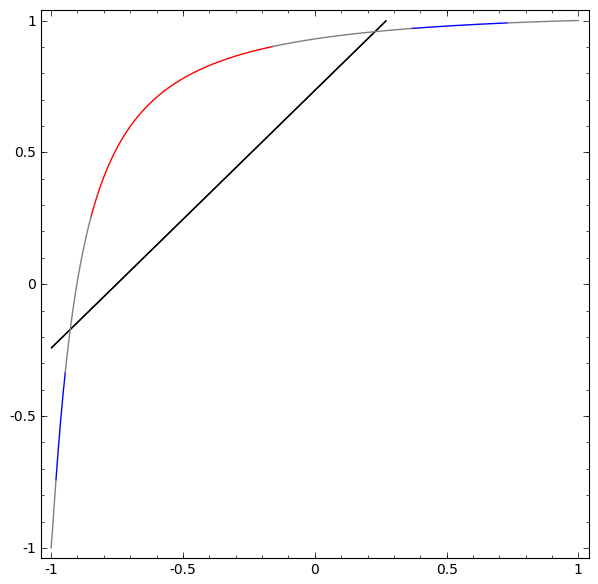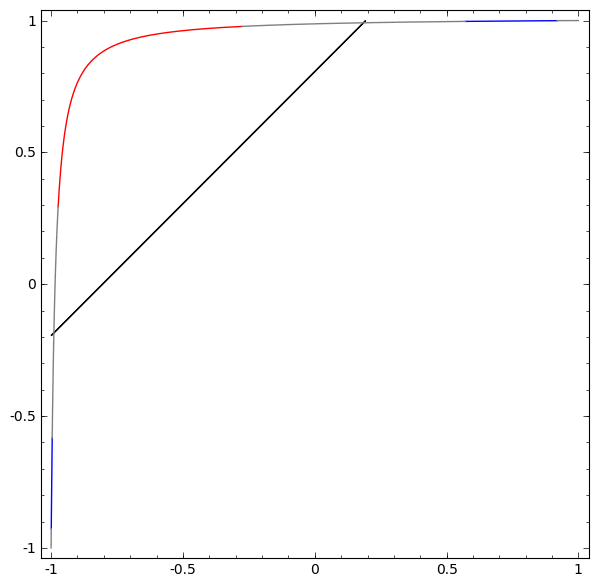
O que está havendo? Um elemento oculto aprende a disparar quando x> -1/2, e um aprende a disparar quando x> 1/2. Quando o primeiro é acionado, mas não o segundo, sabemos que estamos em A.

Conjectura de variedade

Isso se aplica a conjuntos de dados do mundo real, como conjuntos de imagens? Se você é sério sobre a hipótese da diversidade, acho que isso importa.

A hipótese multidimensional é que os dados naturais formam coletores de baixa dimensão no espaço da implantação. Existem razões teóricas [1] e experimentais [2] para acreditar que isso é verdade. Nesse caso, a tarefa do algoritmo de classificação é separar o pacote de variedades entrelaçadas.

Nos exemplos anteriores, uma classe cercava completamente a outra. No entanto, é improvável que a variedade de imagens de cães esteja completamente cercada por uma coleção de imagens de gatos. Mas existem outras situações topológicas mais plausíveis que ainda podem surgir, como veremos na próxima seção.

Conexões e homotopias

Outro conjunto de dados interessante são os dois tori A e B.



Como os conjuntos de dados anteriores que examinamos, esse conjunto de dados não pode ser dividido sem o uso de n + 1 dimensões, a quarta dimensão.

As conexões são estudadas na teoria dos nós, no campo da topologia. Às vezes, quando vemos uma conexão, não fica imediatamente claro se é incoerência (muitas coisas que se enroscam mas podem ser separadas por deformação contínua) ou não.



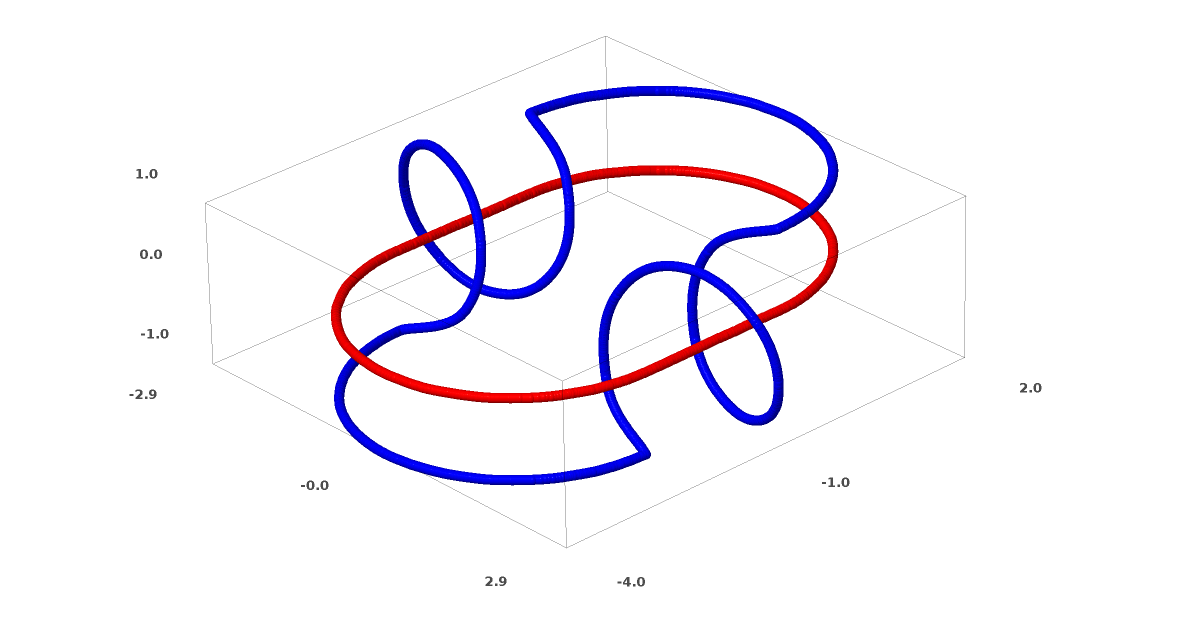
Incoerência relativamente simples.

Se uma rede neural usando camadas com apenas três unidades pode classificá-la, ela é incoerente. (Pergunta: Todas as incoerências podem ser classificadas na rede com apenas três incoerências, teoricamente?)

Do ponto de vista desse nó, a visualização contínua de representações criadas por uma rede neural é um procedimento para desvendar conexões. Em topologia, chamaremos essa isotopia do ambiente entre o link original e os separados.

Formalmente, a isotopia do espaço circundante entre as variedades A e B é uma função contínua F: [0,1] × X → Y, de modo que cada Ft é um homeomorfismo de X até seu intervalo, F0 é uma função de identidade e F1 mapeia A para B. T .e. Ft vai continuamente do mapa A para si mesmo, para o mapa A para B.

Teorema: existe uma isotopia do espaço circundante entre a entrada e a representação do nível da rede se: a) W não é degenerado, b) estamos prontos para transferir neurônios para a camada oculta ec) há mais de um elemento oculto.


Até agora, é improvável que os relacionamentos de que falamos apareçam em dados reais, mas há generalizações de um nível superior. É plausível que esses recursos possam existir em dados reais.

Conexões e nós são coletores unidimensionais, mas precisamos de 4 dimensões para que as redes possam desvendar todos eles. Da mesma forma, pode ser necessário um espaço dimensional ainda mais alto para expandir as variedades n-dimensionais. Todos os coletores n-dimensionais podem ser expandidos em 2n + 2 dimensões. [3]

Saída fácil

A maneira mais fácil é tentar separar os coletores e esticar as peças o mais emaranhadas possível. Embora isso não esteja próximo de uma solução genuína, essa solução pode atingir uma precisão de classificação relativamente alta e ser um mínimo local aceitável.



Esses mínimos locais são absolutamente inúteis em termos de tentativa de resolver problemas topológicos, mas os problemas topológicos podem fornecer uma boa motivação para o estudo desses problemas.

Por outro lado, se estamos interessados ​​apenas em obter bons resultados de classificação, a abordagem é aceitável. Se um pequeno pedaço de um coletor de dados for capturado em outro coletor, isso é um problema? É provável que seja possível obter bons resultados de classificação arbitrariamente, apesar desse problema.

Camadas aprimoradas para manipulação de manifolds?

É difícil imaginar que camadas padrão com transformações afins são realmente boas para manipular variedades.

Talvez faça sentido ter uma camada completamente diferente, que possamos usar em composição com as mais tradicionais?

O estudo de um campo vetorial com uma direção na qual queremos mudar o coletor é promissor:



E então deformamos o espaço com base no campo vetorial:



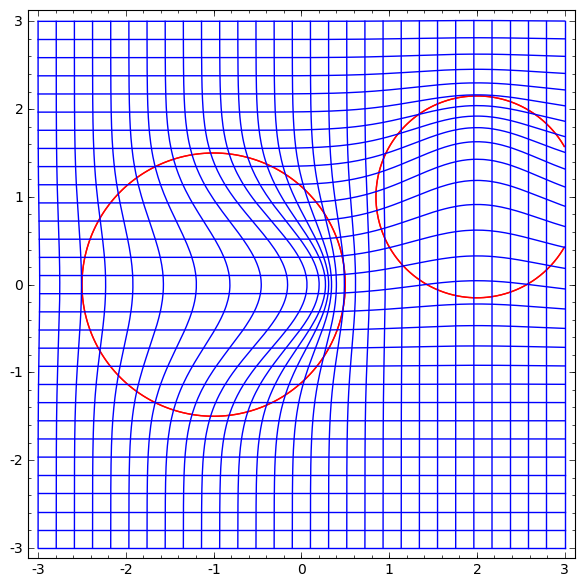
Pode-se estudar o campo vetorial em pontos fixos (basta pegar alguns pontos fixos do conjunto de dados de teste para usar como âncoras) e interpolar de alguma forma.


Onde v0 e v1 são vetores, e f0 (x) e f1 (x) são Gaussianos n-dimensionais.

K-Camadas dos vizinhos mais próximos

A separabilidade linear pode ser uma necessidade enorme e possivelmente irracional de redes neurais. É natural usar o método k-vizinhos mais próximos (k-NN). No entanto, o sucesso do k-NN depende muito da apresentação que classifica; portanto, é necessária uma boa apresentação antes que o k-NN possa funcionar bem.

O k-NN é diferenciável em relação à representação em que atua. Dessa forma, podemos treinar diretamente a rede para classificar o k-NN. Isso pode ser visto como uma espécie de camada “vizinho mais próximo” que atua como uma alternativa ao softmax.
Não queremos avisar com todo o nosso conjunto de treinamento para cada minipartideira, porque será um procedimento muito caro. A abordagem adaptada é classificar cada elemento do minilote com base nas classes dos outros elementos do minilote, atribuindo a cada unidade o peso dividido pela distância da meta de classificação.

Infelizmente, mesmo com arquiteturas complexas, o uso do k-NN reduz a probabilidade de erro - e o uso de arquiteturas mais simples degrada os resultados.

Conclusão

As propriedades topológicas dos dados, como relacionamentos, podem tornar impossível a divisão linear de classes usando redes de baixa dimensão, independentemente da profundidade. Mesmo nos casos em que é tecnicamente possível. Por exemplo, espirais, que podem ser muito difíceis de separar.

Para uma classificação precisa dos dados, as redes neurais precisam de amplas camadas. Além disso, as camadas tradicionais da rede neural são pouco adequadas para representar manipulações importantes com variedades; mesmo se definirmos os pesos manualmente, seria difícil representar de forma compacta as transformações que queremos.