Aprenda o OpenGL. Lição 5.6 - Mapeamento de paralaxe

Mapeamento de paralaxe

A técnica de texturização do Parallax Mapping é um pouco semelhante ao Mapeamento Normal , mas é baseada em um princípio diferente. A semelhança é que, como o Mapeamento Normal, essa técnica aumenta significativamente a complexidade visual e os detalhes da superfície com a textura aplicada ao mesmo tempo, criando uma ilusão plausível da presença de diferenças de altura na superfície. O Parallax Mapping funciona muito bem em conjunto com o Normal Mapping para criar resultados muito confiáveis: a técnica descrita transmite o efeito de alívio muito melhor que o Normal Mapping, e o Normal Mapping o complementa para uma simulação plausível da iluminação dinâmica. O mapeamento de paralaxe dificilmente pode ser considerado uma técnica diretamente relacionada aos métodos de simulação de iluminação, mas mesmo assim escolhi esta seção para considerá-lo, pois o método é um desenvolvimento lógico das idéias do mapeamento normal. Também observo que, para analisar este artigo, é necessário um bom entendimento do algoritmo de mapeamento normal, especialmente o conceito de espaço tangente ou espaço tangente .


O Parallax Mapping pertence à família de técnicas de mapeamento de deslocamento ou de texturas em relevo que compensam os vértices de uma geometria com base nos valores armazenados em mapas de textura especiais. Por exemplo, imagine um plano composto da ordem de mil vértices. Cada uma delas pode ser alterada de acordo com o valor lido na textura, que representa a altura do plano em um determinado ponto. Essa textura, contendo os valores de altura em cada texel, é chamada de mapa de altura . Um exemplo desse mapa, obtido com base nas características geométricas da superfície da alvenaria, é a seguinte imagem:


Amostrando deste mapa e deslocando cada vértice de acordo com o valor da altura, é possível obter uma superfície convexa a partir de um plano ideal que repita os parâmetros geométricos da superfície original. Portanto, pegando um plano com um número suficiente de vértices e aplicando um mapa de altura no exemplo, você pode obter o seguinte resultado:


A abordagem descrita é simples e fácil de implementar, mas requer uma alta densidade de vértices no objeto processado; caso contrário, o resultado da mudança será muito grosseiro. E se em cada superfície plana começarmos a liberar mil ou mais vértices, muito em breve não teremos tempo para renderizar tudo o que precisamos. Talvez exista um algoritmo que permita simular qualitativamente a qualidade do ingênuo algoritmo de mapeamento de deslocamento, mas sem exigir esses custos de geometria? Se você ficar em pé, sente-se, porque na imagem acima existem apenas seis vértices (dois triângulos)! O relevo da alvenaria é perfeitamente imitado graças ao uso do Parallax Mapping, uma técnica de texturização em relevo que não requer muitos vértices para transmitir fielmente o relevo da superfície, mas, como o Normal Mapping, que usa uma abordagem original para enganar os olhos do observador.

A ideia principal da implementação é distorcer as coordenadas de textura do fragmento atual com base na direção do olhar e nos dados do mapa de altura, de modo a criar a ilusão de que esse fragmento pertence a uma parte da superfície mais alta ou mais baixa do que realmente é. Para uma melhor compreensão do princípio, veja o diagrama do nosso exemplo com tijolos:

Aqui, a linha vermelha áspera representa os valores do mapa de altura, refletindo as características geométricas da superfície de alvenaria simulada. Vetor $$$\ color {orange} {\ bar {V}}$ representa a direção da superfície para o observador ( viewDir ). Se o avião estivesse realmente gravado, o observador veria um ponto na superfície $$$\ color {blue} B$ . No entanto, de fato, temos um plano ideal e o raio na direção da vista atravessa o plano em um ponto $$$\ color {green} A$ isso é óbvio. Tarefa de mapeamento de paralaxe para alterar as coordenadas de textura em um ponto $$$\ color {green} A$ para que se tornem idênticas às coordenadas correspondentes ao ponto $$$\ color {blue} B$ . Além disso, para o fragmento atual (corresponde ao ponto $$$\ color {green} A$ ) usamos as coordenadas obtidas do ponto $$$\ color {blue} B$ amostragem de textura é necessária para todos, o que cria a ilusão de que o observador vê um ponto $$$\ color {blue} B$ .

A principal dificuldade está em como calcular as coordenadas de textura de um ponto $$$\ color {blue} B$ estar no ponto $$$\ color {green} A$ . O Parallax Mapping oferece uma solução aproximada usando o simples dimensionamento do vetor de direção da superfície $$$\ color {orange} {\ bar {V}}$ para o observador pela altura do fragmento $$$\ color {green} A$ . I.e. apenas mude o comprimento $$$\ color {orange} {\ bar {V}}$ para que ele corresponda ao tamanho da amostra no mapa de altura $$$\ color {verde} {H (A)}$ correspondente ao fragmento $$$\ color {green} A$ . O diagrama abaixo mostra o resultado da escala - vetor $$$\ color {brown} {\ bar {P}}$ :


Em seguida, o vetor resultante $$$\ color {brown} {\ bar {P}}$ decompostos em componentes de acordo com o sistema de coordenadas do próprio plano, que são usados ​​como compensações para as coordenadas de textura originais. Além disso, como o vetor $$$\ color {brown} {\ bar {P}}$ é calculado usando o valor do mapa de altura, quanto mais o valor da altura corresponder ao fragmento atual, mais forte será o deslocamento para ele.

Essa técnica simples fornece bons resultados em alguns casos, mas ainda é uma estimativa muito aproximada da posição de um ponto $$$\ color {blue} B$ . Se o mapa de altura contiver áreas com valores bastante alterados, o resultado do deslocamento se tornará incorreto: provavelmente o vetor $$$\ color {brown} {\ bar {P}}$ mesmo perto não cairá na vizinhança do ponto $$$\ color {blue} B$ :

Com base no exposto, outra questão permanece: como determinar como projetar corretamente um vetor $$$\ color {brown} {\ bar {P}}$ para uma superfície arbitrariamente orientada para obter componentes para compensar as coordenadas da textura? Seria bom realizar cálculos em um determinado sistema de coordenadas, onde a expansão do vetor $$$\ color {brown} {\ bar {P}}$ nos componentes x e y sempre corresponderiam à base do sistema de coordenadas da textura. Se você elaborou cuidadosamente a lição sobre mapeamento normal , já adivinhou que estamos falando de cálculos no espaço tangente.

Transferindo o vetor da superfície para o observador $$$\ color {orange} {\ bar {V}}$ no espaço tangente, obtemos um vetor modificado $$$\ color {brown} {\ bar {P}}$ , cuja decomposição de componentes será sempre realizada de acordo com os vetores tangentes e bi-tangentes para uma determinada superfície. Como a tangente e a bi-tangente estão sempre alinhadas com os eixos do sistema de coordenadas de textura da superfície, então, independentemente da orientação da superfície, você pode usar com segurança os componentes xey do vetor $$$\ color {brown} {\ bar {P}}$ como deslocamentos para coordenadas de textura.

No entanto, a teoria é suficiente e, depois de arregaçar as mangas, passamos à implementação imediata.

Mapeamento de paralaxe

Para a implementação, usaremos um plano simples com tangentes e tangentes de polarização calculadas para ele - já podemos fazer isso na lição sobre mapeamento normal. Atribuímos vários planos aos planos de textura: difuso , normais e deslocamentos , cada um dos quais está disponível no link apropriado. Na lição, também usaremos o Mapeamento Normal, pois o Parallax Mapping cria a ilusão de uma topografia de superfície, que é facilmente quebrada se a iluminação não mudar de acordo com a topografia. Como os mapas normais geralmente são criados com base em mapas de elevação, seu uso combinado garante a conexão correta da iluminação, levando em consideração o terreno.

Você provavelmente já percebeu que o mapa de deslocamento mostrado no link acima é, de fato, o inverso do mapa mostrado no início da lição. A implementação do Parallax Mapping geralmente é realizada usando apenas esses mapas, que são inversos aos mapas de altura - mapas de profundidade . Isso acontece porque a imitação dos recessos no avião é um pouco mais fácil do que a imitação de elevação. De acordo com essa alteração, o esquema de trabalho do Parallax Mapping também muda:


Mais uma vez, vemos pontos familiares $$$\ color {green} A$ e $$$\ color {blue} B$ entretanto, desta vez o vetor $$$\ color {brown} {\ bar {P}}$ obtido subtraindo o vetor $$$\ color {orange} {\ bar {V}}$ de coordenadas de textura em um ponto $$$\ color {green} A$ . É possível obter profundidades em vez de alturas, subtraindo a amostra de profundidade da unidade ou invertendo as cores da textura em qualquer editor de imagens.

O mapeamento de paralaxe é implementado no sombreador de fragmentos, pois os dados de elevação são diferentes para cada fragmento dentro do triângulo. O código do fragment shader exigirá o cálculo do vetor do fragmento para o observador $$$\ color {orange} {\ bar {V}}$ , então você precisa transmitir a ele a posição do fragmento e do observador no espaço tangente. De acordo com os resultados da lição sobre mapeamento normal, ainda temos o sombreador de vértices em nossas mãos, que transfere todos esses vetores já reduzidos para o espaço tangente, vamos usá-lo:

#version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform mat4 projection; uniform mat4 view; uniform mat4 model; uniform vec3 lightPos; uniform vec3 viewPos; void main() { gl_Position = projection * view * model * vec4(aPos, 1.0); vs_out.FragPos = vec3(model * vec4(aPos, 1.0)); vs_out.TexCoords = aTexCoords; vec3 T = normalize(mat3(model) * aTangent); vec3 B = normalize(mat3(model) * aBitangent); vec3 N = normalize(mat3(model) * aNormal); mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vs_out.FragPos; } 

Das coisas importantes, apenas observarei que, especificamente para as necessidades do mapeamento de paralaxe, é necessário transferir aPos e a posição do observador do viewPos no espaço tangente para o shader de fragmento.

Dentro do shader, implementamos o algoritmo Parallax Mapping, que se parece com isso:

 #version 330 core out vec4 FragColor; in VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } fs_in; uniform sampler2D diffuseMap; uniform sampler2D normalMap; uniform sampler2D depthMap; uniform float height_scale; vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir); void main() { vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos); //       Parallax Mapping vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); //      //     vec3 diffuse = texture(diffuseMap, texCoords); vec3 normal = texture(normalMap, texCoords); normal = normalize(normal * 2.0 - 1.0); //  –     [...] } 

Anunciamos a função ParallaxMapping, que leva as coordenadas de textura do fragmento e o vetor do fragmento para o observador $$$\ color {orange} {\ bar {V}}$ no espaço tangente. O resultado da função são coordenadas de textura deslocadas, que já são usadas para amostras de uma textura difusa e mapa normal. Como resultado, a cor difusa do pixel e seu normal correspondem corretamente à “geometria” alterada do plano.

O que está oculto dentro da função ParallaxMapping?

  vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { float height = texture(depthMap, texCoords).r; vec2 p = viewDir.xy / viewDir.z * (height * height_scale); return texCoords - p; } 

Essa função relativamente simples é uma implementação literal do método, cujos principais pontos discutimos acima. As coordenadas de textura inicial do TexCoords são obtidas , com a ajuda da qual a altura (ou profundidade) é selecionada $$$\ color {verde} {H (A)}$ de depthMap para o fragmento atual. Para calcular o vetor $$$\ color {brown} {\ bar {P}}$ o vetor viewDir é obtido no espaço tangente e o par de seus componentes x e y é dividido pelo componente z , e o resultado é dimensionado pelo valor do deslocamento de leitura da altura . O uniforme height_scale também foi introduzido para fornecer controle adicional sobre a severidade do efeito Mapeamento de Parallax, uma vez que o efeito de deslocamento geralmente é muito forte. Para obter o resultado, subtraímos o vetor resultante $$$\ color {brown} {\ bar {P}}$ das coordenadas originais da textura.

Lidaremos com o momento de dividir viewDir.xy em viewDir.z . Como o vetor viewDir é normalizado, seu componente z fica no intervalo [0, 1]. Quando o vetor é quase paralelo à superfície do componente, z é próximo de zero e a operação de divisão retorna o vetor. $$$\ color {brown} {\ bar {P}}$ muito mais do que se o viewDir estiver próximo da perpendicular à superfície. Em outras palavras, escalamos o vetor $$$\ color {brown} {\ bar {P}}$ para aumentar quando você olha para a superfície em ângulo - isso permite obter um resultado mais realista nesses casos.

Alguns desenvolvedores preferem remover a escala dividindo por viewDir.z , porque, em certos casos, essa abordagem gera resultados incorretos quando vistos de um ângulo. Essa modificação da técnica é chamada de Parallax Mapping with Offset Limiting . A escolha de uma opção de abordagem, na maioria das vezes, continua sendo uma questão de preferência pessoal - por exemplo, sou mais fiel aos resultados do algoritmo Parallax Mapping usual.

As coordenadas de textura alteradas resultantes são usadas para selecionar no mapa difuso e no mapa normal, o que nos dá um bom efeito de distorção da superfície (o parâmetro height_scale aqui é escolhido próximo a 0,1):


Na imagem, você pode comparar os efeitos das técnicas de mapeamento normal e mapeamento de paralaxe. Como o Parallax Mapping simula irregularidades na superfície, são possíveis situações para esta técnica em que os tijolos se sobrepõem, dependendo da direção do olho.

Artefatos estranhos também são visíveis ao longo das bordas do plano texturizado. Eles aparecem devido ao fato de que as coordenadas de textura deslocadas pelo algoritmo Parallax Mapping podem ficar fora do intervalo da unidade e, dependendo do modo de agrupamento , causar resultados indesejados. Uma maneira simples de se livrar desses artefatos é simplesmente descartar todos os fragmentos para os quais as coordenadas de textura estão fora do intervalo da unidade:

 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0) discard; 

Como resultado, todos os fragmentos com coordenadas de textura deslocadas que caem fora do intervalo [0, 1] serão descartados e, visualmente, o resultado da ação Parallax Mapping se tornará aceitável. Obviamente, esse método de rejeição não é universal e pode não ser aplicável a algumas superfícies ou casos de texturização. Mas, no exemplo de um avião, ele funciona perfeitamente e ajuda a fortalecer o efeito de alterar o relevo do avião:


As fontes de amostra estão aqui .

Parece bom e o desempenho do método é excelente - bastava uma amostra adicional da textura! Mas a simplicidade do método tem desvantagens significativas: o efeito de alívio é facilmente destruído quando se olha para o plano em um ângulo (o que também é verdadeiro para o mapeamento normal) ou se há seções no mapa de altura com mudanças acentuadas nos valores:


A razão para a destruição da ilusão está no fato de que o algoritmo é uma aproximação muito aproximada do mapeamento de deslocamento real. No entanto, vários truques adicionais podem nos ajudar, o que nos permite obter resultados quase perfeitos, mesmo ao olhar em ângulo ou ao usar mapas de altura com mudanças bruscas. Por exemplo, podemos usar várias amostras de um mapa de altura para encontrar o ponto mais próximo do ponto $$$\ color {blue} B$ .

Mapeamento íngreme de paralaxe

A técnica Steep Parallax Mapping é um desenvolvimento lógico do clássico Parallax Mapping: a mesma abordagem é usada no algoritmo, mas em vez de uma única seleção, várias são tomadas - para uma melhor aproximação do vetor $$$\ color {brown} {\ bar {P}}$ usado para calcular o ponto $$$\ color {blue} B$ . Devido a essas amostras adicionais, o resultado do algoritmo é visualmente muito mais plausível, mesmo quando se olha para ângulos agudos da superfície.

A base da abordagem Steep PM é pegar uma certa faixa de profundidades e dividi-la em camadas de tamanho igual. Em seguida, iteramos pelas camadas enquanto deslocamos simultaneamente as coordenadas da textura original na direção do vetor $$$\ color {brown} {\ bar {P}}$ e fazer amostras do mapa de profundidade, parando no momento em que a profundidade da amostra é menor que a profundidade da camada atual. Confira o diagrama:


Como você pode ver, passamos pelas camadas de cima para baixo e, para cada camada, comparamos sua profundidade com o valor do mapa de profundidade. Se a profundidade da camada for menor que o valor do mapa de profundidade, isso significa que o vetor $$$\ color {brown} {\ bar {P}}$ correspondente a essa camada está acima da superfície. Esse processo é repetido até que a profundidade da camada seja maior que a seleção do mapa de profundidade: neste momento, o vetor $$$\ color {brown} {\ bar {P}}$ aponta para um ponto abaixo da topografia de superfície simulada.
O exemplo mostra que a seleção do mapa de profundidade na segunda camada ( $$$D (2) = 0,73$ ) ainda permanece "mais profundo" em relação à profundidade da segunda camada igual a 0,4, o que significa que o processo de pesquisa continua. Na próxima passagem, uma profundidade de camada de 0,6 finalmente está "acima" do valor da amostra do mapa de profundidade ( $$$D (3) = 0,37$ ) A partir daqui, concluímos que o vetor $$$\ color {brown} {\ bar {P}}$ obtido para a terceira camada é a posição mais confiável para a geometria distorcida da superfície. Você pode usar coordenadas de textura $$$T_3$ derivado do vetor $$$\ color {brown} {\ bar {P}}$ , para compensar as coordenadas de textura do fragmento atual. Obviamente, a precisão do método aumenta com o número de camadas.

Alterações na implementação afetarão apenas a função ParallaxMapping, pois ela já contém todas as variáveis ​​necessárias para o algoritmo funcionar:

 vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { //    const float numLayers = 10; //    float layerDepth = 1.0 / numLayers; //    float currentLayerDepth = 0.0; //         //     P vec2 P = viewDir.xy * height_scale; vec2 deltaTexCoords = P / numLayers; [...] } 

Primeiro, inicializamos: defina o número de camadas, calcule a profundidade de cada uma delas e, finalmente, encontre o tamanho do deslocamento das coordenadas da textura ao longo da direção do vetor $$$\ color {brown} {\ bar {P}}$ , que precisará ser deslocado em cada camada.

A seguir, é apresentada uma passagem pelas camadas, começando do topo, até encontrar uma seleção do mapa de profundidade que se encontra "acima" do valor da profundidade da camada atual:

 //   vec2 currentTexCoords = texCoords; float currentDepthMapValue = texture(depthMap, currentTexCoords).r; while(currentLayerDepth < currentDepthMapValue) { //      P currentTexCoords -= deltaTexCoords; //          currentDepthMapValue = texture(depthMap, currentTexCoords).r; //     currentLayerDepth += layerDepth; } return currentTexCoords; 

Nesse código, atravessamos todas as camadas de profundidade e alteramos as coordenadas originais da textura até que a seleção do mapa de profundidade seja menor que a profundidade da camada atual. O deslocamento é realizado subtraindo as coordenadas de textura originais do delta com base no vetor $$$\ color {brown} {\ bar {P}}$ . O resultado do algoritmo é um vetor de deslocamento de coordenadas de textura, definido com uma precisão muito maior que o mapeamento Parallax clássico.

Usando cerca de 10 amostras, o exemplo de alvenaria se torna muito mais realista, mesmo quando visto de um ângulo. Mas o melhor de tudo é que as vantagens do Steep PM são visíveis em superfícies com um mapa de profundidade, que apresenta mudanças acentuadas nos valores. Por exemplo, como neste brinquedo de madeira, já demonstrado anteriormente:


Você pode melhorar um pouco mais o algoritmo se analisar um pouco os recursos da técnica de mapeamento de paralaxe. Se você observar a superfície aproximadamente normal, não será necessário alterar fortemente as coordenadas da textura, enquanto, ao olhar para um ângulo, a alteração tenderá ao máximo (imagine mentalmente a direção da vista nos dois casos). Se você parametrizar o número de amostras, dependendo da direção do seu olhar, poderá economizar bastante quando não forem necessárias amostras extras:

 const float minLayers = 8.0; const float maxLayers = 32.0; float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir))); 

O resultado do produto escalar do vetor viewDir e do semi-eixo positivo Z é usado para determinar o número de camadas no intervalo [ minSamples , maxSamples ], ou seja, a direção do olhar determina o número necessário de iterações do efeito (no espaço tangente, o meio eixo positivo Z é direcionado normal à superfície). Se olharmos paralelos à superfície, o efeito usaria todas as 32 camadas.

O código fonte modificado está aqui . Também proponho baixar a textura de um brinquedo de madeira: mapa normal e difuso , mapa de profundidade .

Não sem uma abordagem e desvantagens. Como o número de amostras é o mesmo finito, a aparência de efeitos de aliasing é inevitável, o que faz com que as transições entre as camadas sejam impressionantes:


Você pode reduzir a gravidade do artefato aumentando o número de amostras usadas, mas consome rapidamente todo o desempenho disponível do processador de vídeo. Existem várias adições ao método, que retornam como resultado não o primeiro ponto que apareceu sob o relevo imaginário da superfície, mas o valor interpolado das duas camadas mais próximas, o que nos permite esclarecer melhor a posição do ponto $$$\ color {blue} B$ .

Desses métodos, dois são usados ​​com mais freqüência: Mapeamento de Parallax de Relevo e Mapeamento de Oclusão de Parallax , com o Relief PM fornecendo os resultados mais confiáveis, mas também é um pouco mais exigente no desempenho em comparação com o Mapeamento de Oclusão de Parallax. Como o Mapeamento de oclusão da Parallax ainda possui qualidade muito próxima do Relief PM e, ao mesmo tempo, funciona mais rapidamente, eles preferem usá-lo com mais frequência. A seguir, será considerada a implementação do Mapeamento de Oclusão de Parallax.

Mapeamento de oclusão de paralaxe

O método Parallax Oclusion Mapping funciona de acordo com os mesmos princípios básicos do Steep PM, mas, em vez de usar as coordenadas de textura da primeira camada, onde foi encontrada uma interseção com um relevo imaginário, o método usa interpolação linear entre duas camadas: a camada após e antes da interseção. O coeficiente de ponderação para interpolação linear é baseado na razão entre a profundidade de relevo atual e as profundidades de ambas as camadas em consideração. Dê uma olhada no diagrama para entender melhor como tudo funciona:


Como você pode ver, tudo é muito semelhante ao Steep PM, apenas uma etapa adicional de interpolar as coordenadas de textura das duas camadas de profundidade adjacentes ao ponto de interseção é adicionada. Obviamente, esse método é apenas uma aproximação, mas muito mais preciso que o Steep PM.

O código do Parallax Oclusion Mapping é um complemento ao código Steep PM e não é muito complicado:

 [...] // ,    Steep PM //       , // ..  " " vec2 prevTexCoords = currentTexCoords + deltaTexCoords; //         //      float afterDepth = currentDepthMapValue - currentLayerDepth; float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth; //    float weight = afterDepth / (afterDepth - beforeDepth); vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight); return finalTexCoords; 

No momento em que encontramos a camada após o ponto de interseção com o relevo imaginário, também determinamos as coordenadas de textura da camada antes do ponto de interseção. Em seguida, encontramos os deslocamentos da profundidade de relevo imaginária em relação às profundidades das duas camadas em consideração e usamos sua razão como coeficiente de peso de uma interpolação linear adicional das coordenadas de textura correspondentes às duas camadas consideradas. O resultado da interpolação é retornado pela função para uso futuro.

O mapeamento de oclusão de paralaxe fornece resultados surpreendentemente visualmente confiáveis, embora com pequenas falhas e artefatos de aliasing. Porém, para um comprometimento de velocidade e qualidade, eles são insignificantes e aparecem apenas com uma observação cuidadosa da superfície próxima à câmera ou em ângulos de visão muito nítidos.


Um código de exemplo está aqui .

O Parallax Mapping é realmente uma excelente técnica que permite aumentar drasticamente os detalhes visuais de sua cena, mas, é claro, tem suas desvantagens na forma de artefatos, que vale a pena lembrar ao implementar a técnica no projeto. Na maioria das vezes, o Parallax Mapping é usado em superfícies planas, como paredes ou pisos - onde não é tão fácil determinar o contorno do objeto como um todo, e o ângulo de visão da superfície geralmente fica próximo da perpendicular. Nesse caso, as falhas do Parallax Mapping são quase invisíveis, no contexto de um aumento nos detalhes da superfície.

Bônus do tradutor:

Mapeamento de paralaxe de alívio

Como o autor mencionou dois métodos para esclarecer o resultado do Steep PM, para fins de detalhamento, descreverei a segunda das abordagens.

Como o Parallax Oclusion Mapping, o resultado da execução do Steep PM é usado aqui, ou seja, conhecemos as profundidades de duas camadas entre as quais se encontra o ponto real de interseção do vetor $$$\ color {orange} {\ bar {V}}$ com relevo, bem como as coordenadas correspondentes da textura $$$T_2$ e $$$T_3$ . O refinamento da estimativa do ponto de interseção neste método é devido ao uso da pesquisa binária.

Etapas do algoritmo de refinamento:

• Execute o cálculo íngreme de PM e obtenha coordenadas de textura $$$T_2$ e $$$T_3$ - neste intervalo está o ponto de interseção do vetor $$$\ color {green} {\ bar {V}}$ com topografia de superfície. A interseção verdadeira é marcada com uma cruz vermelha.
• Divida em dois valores atuais para o deslocamento das coordenadas da textura e a altura da camada de profundidade.
• Mover coordenadas de textura do ponto $$$T_3$ na direção oposta ao vetor $$$\ color {green} {\ bar {V}}$ pela quantidade de deslocamento. Reduza a profundidade da camada pelo valor atual do tamanho da camada.
• Pesquisa diretamente binária. O número especificado de iterações é repetido:
• 1. Selecione no mapa de profundidade. Divida o deslocamento da textura atual e o tamanho da camada de profundidade em dois valores atuais.
  2. Se o tamanho da amostra for maior que a profundidade atual da camada, aumente a profundidade da camada pelo tamanho atual e altere as coordenadas da textura ao longo do vetor $$$\ color {green} {\ bar {V}}$ para o deslocamento atual.
  3. Se o tamanho da amostra for menor que a profundidade atual da camada, reduza a profundidade da camada pelo tamanho atual e altere as coordenadas da textura ao longo do vetor inverso $$$\ color {green} {\ bar {V}}$ para o deslocamento atual.
  
  
• As últimas coordenadas de textura obtidas são os resultados do Relief PM.

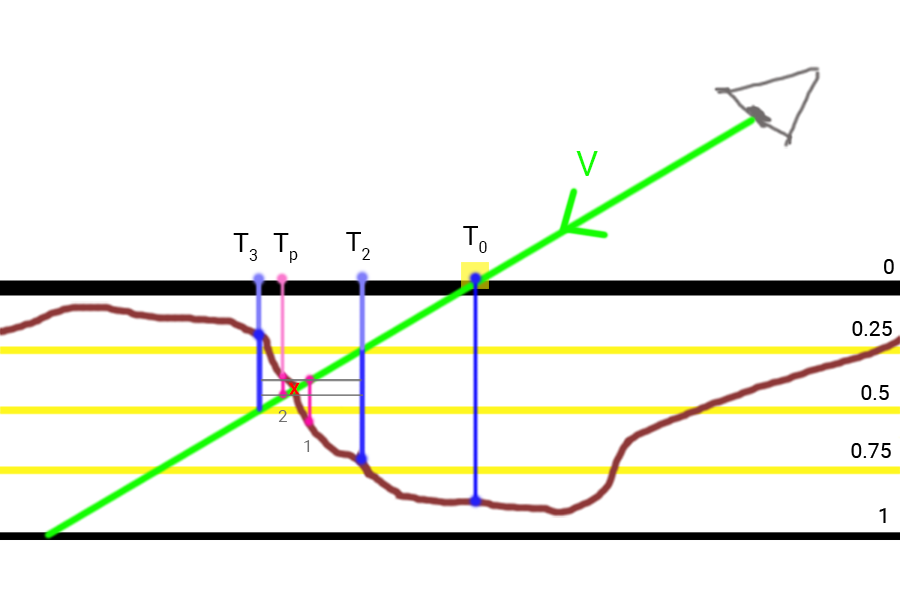
A imagem mostra que depois de encontrar os pontos $$$T_2$ e $$$T_3$ dividimos pela metade o tamanho da camada e o tamanho do deslocamento das coordenadas da textura, o que nos dá o primeiro ponto de iteração da pesquisa binária (1). Como o tamanho da amostra mostrou-se maior que a profundidade atual da camada, reduzimos pela metade os parâmetros novamente e avançamos $$$\ color {green} {\ bar {V}}$ ficando o ponto (2) com coordenadas de textura $$$T_p$ que será o resultado do Steep PM para duas iterações da pesquisa binária.

Código Shader:

 //  : inTexCoords -   , // inViewDir -      - //  : lastDepthValue –      //      vec2 reliefPM(vec2 inTexCoords, vec3 inViewDir, out float lastDepthValue) { // ====== // ,   Steep PM // ====== const float _minLayers = 2.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(dot(vec3(0., 0., 1.), inViewDir))); float deltaDepth = 1./_numLayers; // uDepthScale –     PM vec2 deltaTexcoord = uDepthScale * inViewDir.xy/(inViewDir.z * _numLayers); vec2 currentTexCoords = inTexCoords; float currentLayerDepth = 0.; float currentDepthValue = depthValue(currentTexCoords); while (currentDepthValue > currentLayerDepth) { currentLayerDepth += deltaDepth; currentTexCoords -= deltaTexcoord; currentDepthValue = depthValue(currentTexCoords); } // ====== //   Relief PM // ====== //         deltaTexcoord *= 0.5; deltaDepth *= 0.5; //      ,   Steep PM currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; //    … const int _reliefSteps = 5; int currentStep = _reliefSteps; while (currentStep > 0) { currentDepthValue = depthValue(currentTexCoords); deltaTexcoord *= 0.5; deltaDepth *= 0.5; //       , //       if (currentDepthValue > currentLayerDepth) { currentTexCoords -= deltaTexcoord; currentLayerDepth += deltaDepth; } //       else { currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; } currentStep--; } lastDepthValue = currentDepthValue; return currentTexCoords; } 

Auto-sombreamento

Também uma pequena adição sobre a adição de sombreamento de uma fonte de luz selecionada ao algoritmo de cálculo. Decidi acrescentar, porque tecnicamente o método de cálculo é idêntico aos considerados acima, mas o efeito ainda é interessante e acrescenta detalhes.

De fato, o mesmo PM íngreme é aplicado, mas a pesquisa não vai fundo na superfície simulada ao longo da linha de visão, mas a partir da superfície, ao longo do vetor até a fonte de luz$$$\color{green}{\bar{L}}$ .Esse vetor também é transferido para o espaço tangente e é usado para determinar a quantidade de deslocamento das coordenadas da textura. Na saída do método, um coeficiente de iluminação do material é obtido no intervalo [0, 1], usado para modular os componentes difusos e espelhados nos cálculos de iluminação.
Para definir sombreamento com arestas vivas, basta caminhar ao longo do vetor$$ˉ L até que um ponto fique abaixo da superfície. Assim que esse ponto é encontrado, obtemos o coeficiente de iluminação 0. Se atingimos a profundidade zero sem encontrar um ponto abaixo da superfície, obtemos o coeficiente de iluminação igual a 1.Para determinar o sombreamento com bordas suaves, é necessário verificar vários pontos no vetor$\color{green}{\bar{L}}$

$$ˉ L e localizado abaixo da superfície. O fator de sombreamento é igual à diferença entre a profundidade da camada atual e a profundidade do mapa de profundidade. Também é levada em consideração a remoção do próximo ponto do fragmento em questão na forma de um coeficiente de peso igual a (1,0 - stepIndex / numberOfSteps). Em cada etapa, um coeficiente parcial de iluminação é determinado como:$\color{green}{\bar{L}}$

$$

$$PSF_i=(layerHeight_i - heightFromtexture_i)*(1.0-\frac{i}{numSteps})$$

O resultado final é o fator de luz máximo de todos os parciais:

$$

$$SF=max(PSF_i)$$

O esquema do método:

O progresso do método para três iterações neste exemplo:

• Inicializamos o fator de luz total para zero.
• Dê um passo ao longo do vetor $$ˉ L , chegando ao ponto$\color{green}{\bar{L}}$$$$H_a$ . A profundidade do ponto é claramente menor que a seleção do mapa. $$H ( T G 1 ) - está localizado sob a superfície. Aqui fizemos a primeira verificação e, lembrando o número total de verificações, encontramos e salvamos o primeiro fator de luz parcial: (1.0 - 1.0 / 3.0).$H(T_{L1})$
• Dê um passo ao longo do vetor $$ˉ L , chegando ao ponto$\color{green}{\bar{L}}$$$$H_b$ . A profundidade do ponto é claramente menor que a seleção do mapa. $$H ( T G 2 ) - é, sob a superfície. A segunda verificação e o segundo coeficiente parcial: (1.0 - 2.0 / 3.0).$H(T_{L2})$
• Demos mais um passo ao longo do vetor e chegamos à profundidade mínima de 0. Pare o movimento.
• Definição do resultado: se nenhum ponto foi encontrado sob a superfície, retornamos um coeficiente igual a 1 (sem sombreamento). Caso contrário, o coeficiente resultante se tornará o máximo dos parciais calculados. Para uso em cálculos de iluminação, subtraímos esse valor da unidade.

Exemplo de código de sombreador:

 //  : inTexCoords -   , // inLightDir -       - //  : inLastDepth –    , //      PM //       //    float getParallaxSelfShadow(vec2 inTexCoords, vec3 inLightDir, float inLastDepth) { float shadowMultiplier = 0.; //      , //    float alignFactor = dot(vec3(0., 0., 1.), inLightDir); if (alignFactor > 0.) { //   :  ,  //  ,     const float _minLayers = 16.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(alignFactor)); float _dDepth = inLastDepth/_numLayers; vec2 _dtex = uDepthScale * inLightDir.xy/(inLightDir.z * _numLayers); //  ,    int numSamplesUnderSurface = 0; //       //     L float currentLayerDepth = inLastDepth - _dDepth; vec2 currentTexCoords = inTexCoords + _dtex; float currentDepthValue = depthValue(currentTexCoords); //    float stepIndex = 1.; // ,       … while (currentLayerDepth > 0.) { //     ,     //       if (currentDepthValue < currentLayerDepth) { numSamplesUnderSurface++; float currentShadowMultiplier = (currentLayerDepth - currentDepthValue)*(1. - stepIndex/_numLayers); shadowMultiplier = max(shadowMultiplier, currentShadowMultiplier); } stepIndex++; currentLayerDepth -= _dDepth; currentTexCoords += _dtex; currentDepthValue = depthValue(currentTexCoords); } //      ,   //      1 if (numSamplesUnderSurface < 1) shadowMultiplier = 1.; else shadowMultiplier = 1. - shadowMultiplier; } return shadowMultiplier; } 

O coeficiente resultante é usado para modular o resultado do modelo de iluminação Blinn-Fong usado nos exemplos:

 [...] //      vec3 fullColorADS = ambientTerm + attenuation * (diffuseTerm + specularTerm); //     -  fullColorADS *= pmShadowMultiplier; return fullColorADS; 

Comparação de todos os métodos em uma colagem, volume de 3 MB.

Também uma comparação de vídeo:

Materiais adicionais

• Mapeamento de oclusão de paralaxe no GLSL : uma ótima lição de mapeamento de paralaxe de sunandblackcat.com .
• Como funciona o mapeamento de deslocamento de paralaxe : um tutorial em vídeo que explica os detalhes do mapeamento de paralaxe por TheBennyBox .

PS : Temos um telegrama conf para coordenação de transferências. Se você tem um desejo sério de ajudar com a tradução, é bem-vindo!