👴 💛 🏂 Fórmula de Tupper e implementação do algoritmo em Python 🥙 💪 🤤

Em vez do prefácio

Há pouco tempo, na Internet, aprendi sobre uma cópia tão maravilhosa e surpreendente da biblioteca da Babilônia como a fórmula Tapper . Pelo contrário, é mais desigualdade de Tupper do que a fórmula. A peculiaridade dessa desigualdade é que ela cria sua própria imagem no gráfico. Basta olhar para este milagre!

imagem

(Fonte da Wikipedia)

O que você vê na imagem é a fórmula do mesmo Jeff Tupper. Provavelmente, metade dos leitores já foi ao tungstênio para obter o resultado dessa desigualdade ... Mas isso não é tão simples. Como você pode ver nesta imagem, a fórmula no gráfico pode ser vista em um segmento ao longo do eixo OY [k; k + 15]. Qual é esse número misterioso k? Onde conseguir? O fato é que essa desigualdade, de acordo com o conceito da biblioteca babilônica, pode exibir absolutamente qualquer imagem com uma resolução de 106x17! Cada imagem tem sua própria posição no gráfico e, portanto, possui um número único k. Assim, para cada número k, há uma única imagem no gráfico inteiro !

Para uma determinada imagem, o número k é o seguinte:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

É interessante olhar para as pessoas que irão rolar até essa coordenada para ver a fórmula

Ocorreu-me escrever um programa em Python3 que convertesse uma imagem em um número ke vice-versa e falasse sobre outra ótima maneira de codificar uma imagem em um número.

Teoria

(Adicionado) Como isso funciona?

Vamos dar uma olhada na própria fórmula:
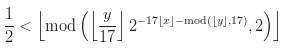
imagem

Vamos definir sua sintaxe:
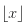
imagem

- número arredondado para baixo
mod (x, y) - restante da divisão de x por y

E então, ao que parece, tudo está claro.
Observe que x e y são arredondados para baixo. É esse arredondamento que nos dá uma imagem de pixel
imagem

Denote tudo o que é arredondado no lado direito da desigualdade por

a l p h a

$\ alpha$ .
Então

1 / 2 < [a l p h a] <=> 1 <= [a l p h a]

$1/2 <[\ alpha] <=> 1 <= [\ alpha]$

O que é óbvio, porque toda a expressão é arredondada para baixo.

Seja y = 17r + q, onde r é a parte inteira da divisão de y por 17 e r é o restante da divisão. Assim, podemos substituir na fórmula

[y / 17]

$[y / 17]$ em r e

m o d (y, 17)

$mod (y, 17)$ em q.

Nós temos

1 <= m o d (q * 2^{- 17 - r}, 2)

$1 <= mod (q * 2 ^ {- 17-r}, 2)$

Ou então

1 <= m o d (q / 2^{17 x + r}, 2)

$1 <= mod (q / 2 ^ {17x + r}, 2)$

mod (

a l p h a

$\ alpha$ , 2) recebe 2 valores - 0 ou 1. Portanto, essa desigualdade dirá se o número

q / 2^{17 x + r}

$q / 2 ^ {17x + r}$ mesmo ou não.

Observe que a imagem é visualizada no intervalo [N, N + 16], respectivamente

q = [y / 17]

$q = [y / 17]$ permanece constante em toda a altura da imagem, o que não pode ser dito sobre o número r (em toda a imagem varia de 0 a 16).

E agora a cereja no bolo. Número

[q / 2^{17 x + r}]

$[q / {2 ^ {17x + r}}]$ será ímpar se e somente se o número do bit (17x + r) na representação binária de q for igual a 1. E como o número q está constantemente mudando com sua altura e sua representação binária, obtemos sempre uma imagem única! É exatamente isso que a fórmula de Tapper funciona.

Agora vamos ver como calcular a altura em que queremos ver nossa imagem

O princípio do cálculo do número k

O próprio Tupper descreveu o cálculo do número k para qualquer imagem de 106x17 (isso é importante!) Da seguinte maneira:

Converter imagem em preto e branco
Leia cada pixel de baixo para cima, da esquerda para a direita e coloque-o no buffer. Se o pixel for preto - coloque 1, se branco - 0.
Converta binário em decimal e multiplique por 17
Lucro!

Para obter uma imagem do número k, fazemos tudo exatamente o oposto. Bem, vamos codificar!

Kodim

UPD: Nos comentários, as pessoas melhoraram um pouco o código, tornaram-no mais simples e mais transparente. Este artigo publicou dados de atualização. Se você quiser ver as versões antigas do código - vá para o repositório do github (até você confirmar, vincule no final do artigo) e no comentário

De k à imagem

UPD

A pedido dos comentaristas, foi adicionada uma nova maneira de calcular a imagem usando essa desigualdade ek! Agora não vamos fazer manipulações com o número, transferir para o sistema binário, mas afetar diretamente a própria função!

Usando o método do comutador para decodificar o número k

Obtemos o número k do usuário, ~~com os olhos fechados, o~~ dividimos por 17 e o traduzimos no sistema binário.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:]

Entendemos que alguns pixels iniciais podem ser brancos (iguais a 0), respectivamente, para o nosso número binário, os primeiros bits serão zeros e, ao converter um número em um sistema decimal, esses zeros iniciais serão perdidos. Portanto, verificamos o tamanho do número binário resultante, se for menor que 1802, e adicionamos zeros ao início.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary

Em seguida, declare uma lista bidimensional na qual armazenaremos informações sobre cada linha da imagem. Em seguida, anotamos todos os bits que lemos (não se esqueça do algoritmo pelo qual o número k é criado - de baixo para cima, da esquerda para a direita)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #

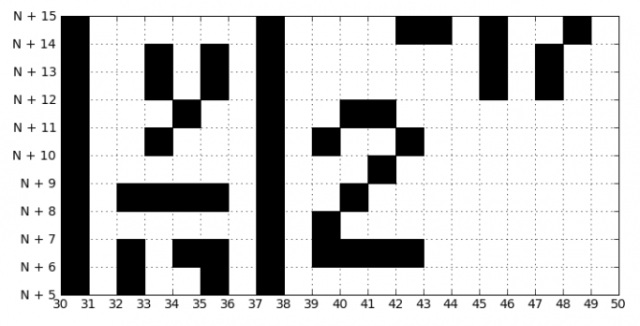
Vamos tentar inserir o número k, que eu indiquei no início do artigo, em nosso programa e obter o seguinte:

imagem

Como você pode ver, tudo deu certo para nós, e agora podemos decodificar qualquer k!

Usando desigualdade para gerar uma imagem de k

Primeiro, escreva a função em python:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2

Graças aos operadores // e <<, a implementação da função foi bastante simplificada. É garantido que os números x e y serão inteiros !

Novamente, criamos uma lista bidimensional, onde armazenamos os bits da imagem e escrevemos informações sobre cada linha usando loops.

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2))

E então, como no exemplo anterior, desenhamos uma imagem usando a biblioteca PIL.

A função completa é assim:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists

Imagem em k

Bem, agora aprenderemos a codificar qualquer imagem no número k.

Primeiro obtemos a própria imagem

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im

Verifique seu tamanho

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !")

Tornamos a imagem em preto e branco e começamos a ler pixel por pixel:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0'

Resta apenas converter para o sistema decimal e multiplicar por 17.

 k = int(byteset,2)*17 print(" :") print(k)

Bem, vamos testar!

Decidi codificar o logotipo habr. Aqui está a imagem de origem:

imagem

Iniciamos o programa e especificamos o nome da imagem:

imagem

Temos o seguinte k:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

Vamos dar uma olhada em nosso próprio programa.

Aqui está a imagem que recebemos:

imagem

Estava um pouco distorcido devido a uma tradução ligeiramente torta da imagem em preto e branco.

Sumário

Código fonte: Github

Fontes: artigo da Wiki

Fórmula de Tupper e implementação do algoritmo em Python