Em um artigo recente, “
Modulação em amplitude de um sinal arbitrário ”
, seu autor tentou confusamente apresentar sua compreensão da formação do espectro com modulação em amplitude. Mas a falta de ilustrações e um excesso de matemática envolvendo transformações integrais impediram a comunidade de entender os pensamentos do autor e apreciar o artigo; embora o tópico seja bastante simples - e tentaremos considerá-lo novamente, desta vez com fotos e Wolfram Mathematica.
Portanto, a idéia da modulação de amplitude é transmitir um sinal de baixa frequência - voz ou música - modulando um sinal de alta frequência (portadora), muitas vezes excedendo a faixa audível e ocupando uma estreita faixa de frequência no ar. A modulação em si é realizada simplesmente multiplicando o sinal pela operadora:

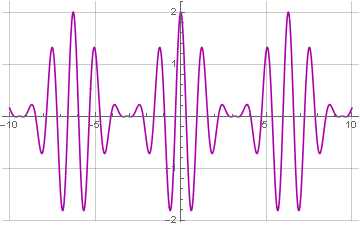
Aqui temos uma onda senoidal com uma frequência de 5:


E o próprio sinal - com uma frequência de 1:

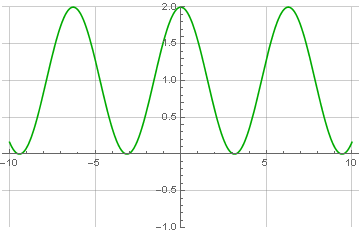
Você pode perceber que o sinal foi alterado e possui apenas valores positivos. Isso não é acidental e é um pré-requisito para a possibilidade de sua subsequente restauração correta. Como restaurá-lo? Muito fácil! É necessário mudar a fase do sinal modulado em 90 graus (a operação conhecida como
transformada de Hilbert ) e calcular a raiz da soma dos quadrados dos sinais modulados e convertidos:

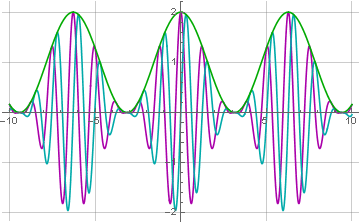
Em uma versão mais simples (mas aproximada), a transformação Hilbert pode ser substituída por um atraso de sinal em um quarto do período de frequência da operadora, e o sinal final pode ser adicionalmente filtrado por um filtro passa-baixo. Em uma versão ainda mais simples, você não pode contar as raízes e os quadrados, mas filtrar o sinal pelo valor absoluto (que geralmente é usado em receptores de rádio).
Agora vamos ver o que acontece com os espectros. Calculamos a transformada de Fourier da transportadora:


Como a função delta Dirac não é uma função no sentido clássico, seu gráfico não pode ser construído de maneira padrão; portanto, faremos isso manualmente, usando o estilo geralmente aceito:

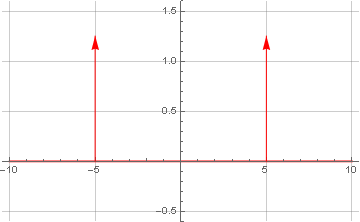
Espera-se que receba a mesma frequência da fórmula inicial. A presença de mais uma da mesma frequência, mas com um sinal de menos, não é acidental - esse fenômeno é chamado de
simetria hermitiana e é uma conseqüência do fato de que a função em questão é puramente real e na representação complexa tem um componente imaginário zero. A ausência de componentes imaginários no espectro após a transformação se deve ao fato de inicialmente nossas funções serem pares (simétricas em relação a zero).
Agora fazemos a transformada de Fourier para o próprio sinal:



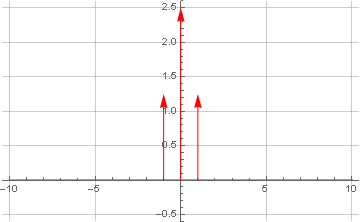
Aqui também obtivemos a função delta Dirac no centro de coordenadas - devido à presença de um componente constante no sinal, que não possui oscilações por definição - o que nos permite considerá-la como uma frequência zero.
O que acontecerá com o espectro se eles forem multiplicados? Vamos ver:



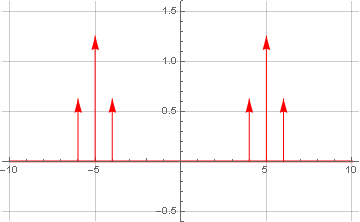
Teoricamente, sabemos que a multiplicação no domínio do tempo é equivalente a convolução no domínio da frequência (e vice-versa, amplamente utilizado na filtragem FIR). E como um dos sinais sujeitos à convolução consistia em apenas uma frequência (positiva e negativa), como resultado da convolução, obtivemos apenas uma transferência linear do sinal para cima na frequência (nas duas direções). E como a simetria permaneceu, o sinal ainda não possui um componente imaginário.
Agora, nós o trazemos para uma forma complexa (
analítica ), zerando a faixa de frequência negativa:

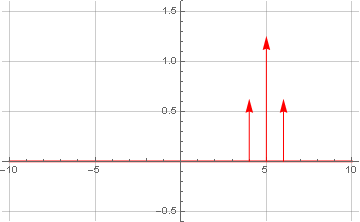
e faça a transformação inversa de Fourier:


Como a função agora é complexa, para construir seu gráfico, é necessário extrair separadamente os componentes reais e imaginários:

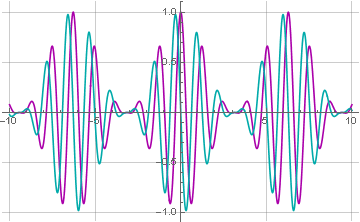
Agora nosso sinal tem um componente imaginário, que é o sinal original alterado em 90 graus. Isso será mais óbvio se representarmos a função resultante em uma forma trigonométrica:

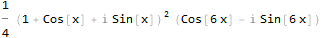
Ainda não é muito óbvio. Vamos tentar simplificar:

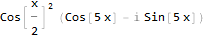
Agora parece mais a verdade - e como você pode ver, a função do nosso sinal original também foi simplificada. Vamos tentar devolvê-lo à sua forma original:
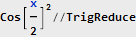

O fator 1/2 não apareceu por acaso - depois de zerar metade do espectro, reduzimos a potência do sinal. Bem, agora, tendo um sinal complexo modulado, podemos usar este módulo para calcular:

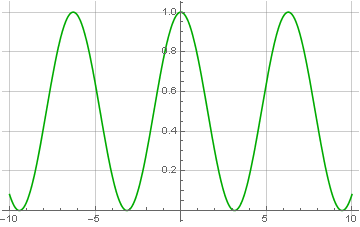
O módulo de um número complexo é calculado com precisão através da raiz da soma dos quadrados dos componentes imaginários e reais. E a partir disso, fica claro por que o sinal codificado deve consistir apenas em valores positivos - se incluir valores negativos, depois da restauração eles também se tornarão positivos, o que é chamado de supermodulação:

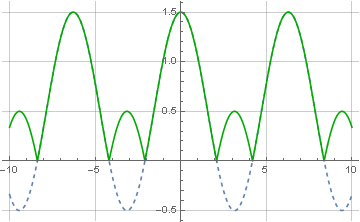
A recuperação do sinal também é possível com a ajuda de um oscilador local em quadratura - quando o sinal modulado é novamente multiplicado pela frequência da portadora, mas desta vez é complexo:





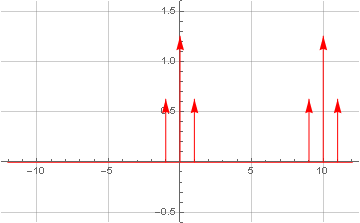
Devido ao fato de que a frequência complexa no domínio da frequência possui apenas um pulso sem duplicá-lo na faixa de frequência negativa, como resultado da convolução, obtemos uma transferência linear de espectro, na qual a parte negativa do espectro volta ao centro e a positiva se move ainda mais, e ele será filtrado apenas por um filtro passa-baixo.
Conclusão
Como você pode ver, não há nada complicado em considerar a modulação de amplitude através da transformada de Fourier; se considerarmos exclusivamente no nível escolar, basta lembrar que o produto da soma (portadora) (representando o sinal na forma de uma série trigonométrica) é equivalente à soma dos produtos (cada membro da série individualmente na frequência da portadora) - e, portanto, cada um desses produtos é decomposto em a soma de dois sinusoides de acordo com a fórmula já expressa pelo autor do artigo original.
Um leitor atento também pode perceber que, como a modulação resultou em um espectro simétrico em relação à frequência da portadora, isso significa que há redundância de dados e você pode deixar apenas uma banda lateral, reduzindo a faixa de frequência ocupada no ar. Essa tecnologia
existe , mas essa é uma história completamente diferente.