Saudações a todos e, especialmente, aos interessados em matemática discreta e teoria de grafos.
Antecedentes
Aconteceu que, motivado pelo interesse, eu estava desenvolvendo um serviço de construção de excursões. rotas. A tarefa era planejar as melhores rotas com base na cidade de interesse do usuário, nas categorias de estabelecimentos e no prazo. Bem, uma das subtarefas era calcular o tempo de viagem de uma instituição para outra. Como eu era jovem e estúpido, resolvi esse problema de frente, com o algoritmo de Dijkstra, mas, para ser justo, é importante notar que somente com ele foi possível iniciar a iteração de um nó para milhares de outros, o armazenamento em cache dessas distâncias não era uma opção, apenas mais de 10k em estabelecimentos Somente Moscou, e decisões como a distância de Manhattan em nossas cidades não funcionam de todo.
E, portanto, foi possível resolver o problema de desempenho no problema combinatório, mas a maior parte do tempo para processar a solicitação era gasta na procura de caminhos não armazenados em cache. O problema foi complicado pelo fato de o gráfico da estrada Osm em Moscou ser bastante grande (meio milhão de nós e 1,1 milhão de arcos).
Não falarei sobre todas as tentativas e que, de fato, o problema poderia ser resolvido aparando os arcos extras do gráfico, só lhe direi que em algum momento ocorreu-me e percebi que se você abordar o algoritmo de Dijkstra em termos da abordagem probabilística, então pode ser linear.
Dijkstra por tempo logarítmico
Todo mundo sabe, mas quem sabe, leu o algoritmo de Dijkstra usando uma fila com a complexidade logarítmica de inserção e exclusão pode levar à complexidade do formato O (n log (n) + m log (n)). Ao usar o heap de Fibonacci, a complexidade pode ser reduzida para O (n * log (n) + m), mas ainda não linear, mas eu gostaria.
No caso geral, o algoritmo de fila é descrito da seguinte maneira:
Vamos:
- V é o conjunto de vértices do gráfico
- E é o conjunto de arestas do gráfico
- w [i, j] é o peso da aresta do nó i ao nó j
- a - inicia o vértice da pesquisa
- fila q-vértice
- d [i] - distância ao i-ésimo nó
- d [a] = 0, para todos os outros d [i] = + inf
Enquanto q não estiver vazio:
- v é o vértice com o mínimo d [v] de q
- Para todos os vértices u para os quais existe uma transição para E do vértice v
- se d [u]> w [vu] + d [v]
- remova u de q com distância d [u]
- d [u] = w [vu] + d [v]
- adicione u a q com distância d [u]
- remover v de q
Se usarmos uma árvore vermelho-preta como uma fila, onde a inserção e a exclusão ocorrem no log (n), e a busca pelo elemento mínimo é semelhante no log (n), a complexidade do algoritmo é O (n log (n) + m log (n)) .
E aqui vale a pena notar uma característica importante: nada impede, em teoria, considerar o topo várias vezes. Se o vértice foi examinado e a distância a ele foi atualizada para um valor incorreto, maior que o valor real, desde que, mais cedo ou mais tarde, o sistema converja e a distância para u seja atualizada para o valor correto, é permitido fazer esses truques. Mas vale a pena notar - um vértice deve ser considerado mais de uma vez com baixa probabilidade.
Classificar tabela de hash
Para reduzir o tempo de execução do algoritmo Dijkstra para um linear, é proposta uma estrutura de dados, que é uma tabela de hash com números de nós (node_id) como valores. Observo que a necessidade da matriz d não desaparece, ainda é necessário obter a distância para o i-ésimo nó em tempo constante.
A figura abaixo mostra um exemplo da estrutura proposta.
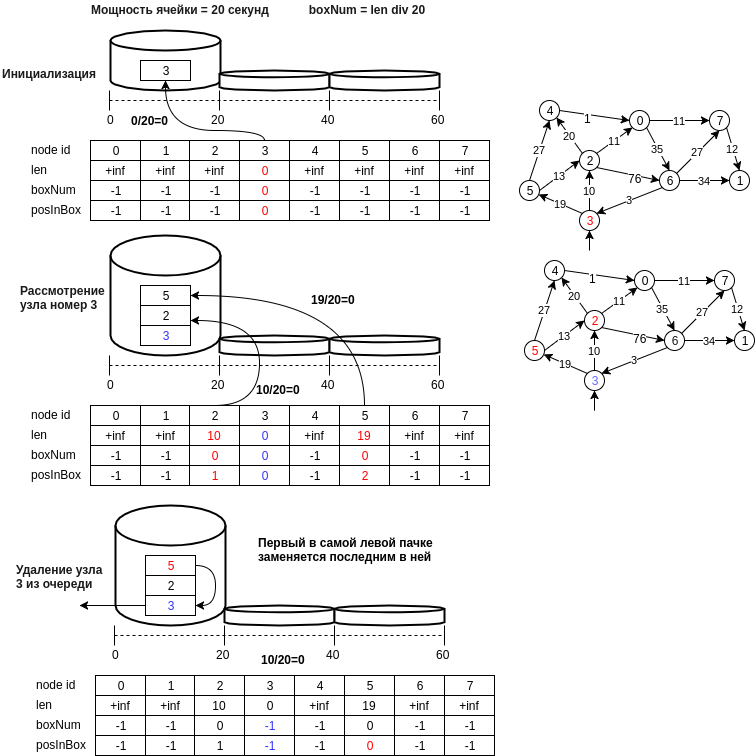
Vamos descrever em etapas a estrutura de dados proposta:
- o nó u é gravado na célula com um número igual a d [u] // bucket_size, em que bucket_size é a potência da célula (por exemplo, 20 metros, ou seja, a célula no número 0 conterá nós cuja distância estará no intervalo [0, 20) metros )
- o último nó da primeira célula não vazia, ou seja, a operação de extração do elemento mínimo será realizada em O (1). É necessário manter o estado atual do identificador do número da primeira célula não vazia (min_el).
- a operação de inserção é executada adicionando um novo número de nó ao final da célula e também executando O (1), porque o cálculo do número de células ocorre em um tempo constante.
- a operação de exclusão, como no caso de uma tabela de hash, é possível uma enumeração normal, e pode-se fazer uma suposição e dizer que, com um tamanho de célula pequeno, isso também é O (1). Se você não se importa com a memória (em princípio, e não é necessário muito, outra matriz por n), é possível criar uma matriz de posições na célula. Nesse caso, se o elemento for excluído no meio da célula, é necessário mover o último valor da célula para o local excluído.
- um ponto importante ao escolher o elemento mínimo: é mínimo apenas com alguma probabilidade, mas o algoritmo examinará a célula min_el até que ela fique vazia e, mais cedo ou mais tarde, o elemento mínimo real será considerado, e se atualizarmos acidentalmente o valor da distância até o nó acessível mínimo, os nós adjacentes ao mínimo podem estar novamente na fila e a distância até eles estará correta etc.
- Você também pode excluir células vazias até min_el, economizando memória. Nesse caso, a remoção do nó v da fila q deve ser feita somente após considerar todos os nós adjacentes.
- e você também pode alterar a potência da célula, os parâmetros para aumentar o tamanho da célula e o número de células quando precisar aumentar o tamanho da tabela de hash.
Resultados da medição
Verificações foram feitas no mapa osm de Moscou, descarregadas via osm2po no postgres e depois carregadas na memória. Os testes foram escritos em Java. Havia 3 versões do gráfico:
- gráfico de origem - 0,43 milhão de nós, 1,14 milhão de arcos
- versão compactada do gráfico com 173k nós e 750k arcos
- versão pedestre da versão compactada do gráfico, 450k arcos, 100k nós.
Abaixo está uma imagem com medidas em diferentes versões do gráfico:

Considere a dependência da probabilidade de visualizar novamente o vértice e o tamanho do gráfico:
| número de visualizações de nó | contar vértices | probabilidade de revisar novamente o nó |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0,9 |
| 431490 | 419594 | 2.8 |
Você pode perceber que a probabilidade não depende do tamanho do gráfico e é bastante específica para a solicitação, mas é pequena e seu alcance é configurado alterando a potência da célula. Ficaria muito grato por ajudar na construção de uma modificação probabilística do algoritmo com parâmetros que garantam um intervalo de confiança dentro do intervalo em que a probabilidade de visualização repetida não excederá uma certa porcentagem.
Também foram realizadas medidas qualitativas para confirmar praticamente a comparação da exatidão do resultado dos algoritmos com a nova estrutura de dados, que mostrou completa coincidência do menor comprimento do caminho, de 1000 nós aleatórios a 1000 outros nós aleatórios no gráfico. (e assim por diante 250 iterações) ao trabalhar com uma tabela de hash de classificação e uma árvore vermelho-preta.
O código fonte da estrutura de dados proposta está localizado no link
PS: Conheço o algoritmo Torup e o fato de ele resolver o mesmo problema em tempo linear, mas não consegui dominar esse trabalho fundamental em uma noite, apesar de entender a ideia em termos gerais. Pelo menos, pelo que entendi, outra abordagem é proposta lá, com base na construção de uma árvore de abrangência mínima.
PSS Dentro de uma semana, tentarei encontrar tempo e fazer uma comparação com o grupo Fibonacci e, um pouco mais tarde, adicionar o nabo do github com exemplos e códigos de teste.