Ao resolver os problemas de transmissão de dados através de linhas representadas por características de frequência, são aplicadas as transformadas de Fourier - a transferência de sinais do domínio do tempo para o domínio da frequência e vice-versa. O ambiente MATLAB possui um conjunto completo de funções para resolver esses problemas. Neste trabalho, é analisado um exemplo de cálculo no MATLAB da reação de um sinal transmitido através de uma linha cuja característica é medida em frequências que não coincidem com a frequência de transferência de dados. Espero que este exemplo facilite a compreensão dos recursos da tecnologia de conversão de sinal no ambiente MATLAB.
Condição da tarefa
É necessário determinar a alteração na forma do sinal digital binário que passa através do filtro e da linha de sinal. O sinal é definido pela amplitude e taxa de transmissão. O filtro de segunda ordem, normalizado para a frequência de transferência de dados, é definido por constantes de tempo. A função de transferência da linha de sinal é representada pela resposta de frequência medida em forma complexa.
O ambiente usado para calcular e exibir dados é o MATLAB R2015a.
As seguintes relações publicadas no site
www.StatEye.org para a versão do método StatEye 3.0 GUI [1, 2, 3] foram tomadas como exemplo dos dados iniciais.
Taxa de dados bps = 10,3125 Gbit / s. As constantes de tempo do filtro normalizado de segunda ordem são as mesmas, e recíproco é ¾ da frequência de transmissão de dados. A linha de sinal é representada por uma resposta de frequência. A característica foi medida no canal f = 0,006495: 0,0012475: 20 GHz. O número especificado de pontos de amostragem da transformação de Fourier: points = 2 ^ 13.
A Figura 1 mostra os resultados da transferência de dados, sequência e processamento de dados discutidos neste documento. A transição do domínio do tempo para o domínio da frequência e vice-versa é realizada usando o algoritmo Fast Fourier Transform (FFT).
Figura 1. Canal de dados. Sinal de entrada iSignal.Tx, sinal de saída do filtro iSignal.Filter_out, linha de sinal de saída iSignal.Rx. As características mostradas no diagrama são discutidas abaixo.Sequência de cálculo
Neste trabalho, os principais cálculos são realizados no domínio da frequência. Para isso, o sinal original do domínio do tempo foi transferido para o domínio da frequência usando a transformada de Fourier, multiplicando as características espectrais do sinal, o filtro e a linha de sinal, foi encontrado o sinal de saída do caminho, que é transferido do domínio da frequência para o domínio do tempo pela transformação inversa de Fourier.
A taxa de transferência de dados é duas vezes maior que a frequência na qual os dados são transmitidos. A frequência máxima da linha de sinal medida max (canal.f) = 20 GHz. Nessa frequência, os dados podem ser transmitidos a uma velocidade de 40 Gbit / s (como 2 * max (canal.f)).
A taxa máxima de transferência de dados, que não excede a taxa máxima de transmissão na linha de sinal de 40 Gbit / s e uma taxa de transmissão múltipla de bps = 10,3125 Gbit / s, é fmax = 30,9375 Gbit / s, a multiplicidade N = 3 (N = fmax / bps). Além disso, fmax é usado como frequência limitadora para calcular a resposta do sinal usando a transformada de Fourier.
Conversão do sinal de entrada no domínio da frequência
Discriminação de tempo para a construção do sinal de entrada (bit de dados) no domínio do tempo Ts = 1 / fmax; Ts = 3,232e-11 s. Normalizada em relação à duração do sinal, a escala de tempo consiste em 2 ^ 13 pontos (pontos), a escala inclui a seguinte matriz de pontos tempo = bps / Ts. * (1: pontos). Um sinal único discreto a uma taxa de transmissão de bps = 10,3125 Gbit / se quantização com um período Ts = 1 / fmax consiste em três pontos na faixa de 10 a 11 unidades de tempo normalizado. Um sinal de amplitude da unidade pode ser construído em qualquer outro lugar na linha do tempo, mas é melhor recuar das bordas para ver completamente o plano de fundo e o processo de transição do sinal de saída. Um sinal de pulso (bit de dados) construído usando os seguintes comandos do MATLAB é mostrado na Figura 2.
iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;
Figura 2. Sinal de pulso de entrada iSignal.Tx, bit de dados.A conversão do sinal iSignal.Tx no domínio da frequência é realizada pelas seguintes funções FFT.
iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);
A função de transformação de Fourier fft constrói um espectro simétrico do sinal nas regiões de frequências positivas e negativas, cuja frequência máxima está no centro do espectro (veja a Figura 3). A função fftshift restaura o espectro deslocando para o centro a frequência do sinal zero, como mostra a Figura 4.
A resolução da frequência do espectro é fs = fmax / pontos; As frequências de espectro variam de -fmax / 2 a fmax / 2-fs e são iguais a f = -fmax / 2: fs: fmax / 2-fs;
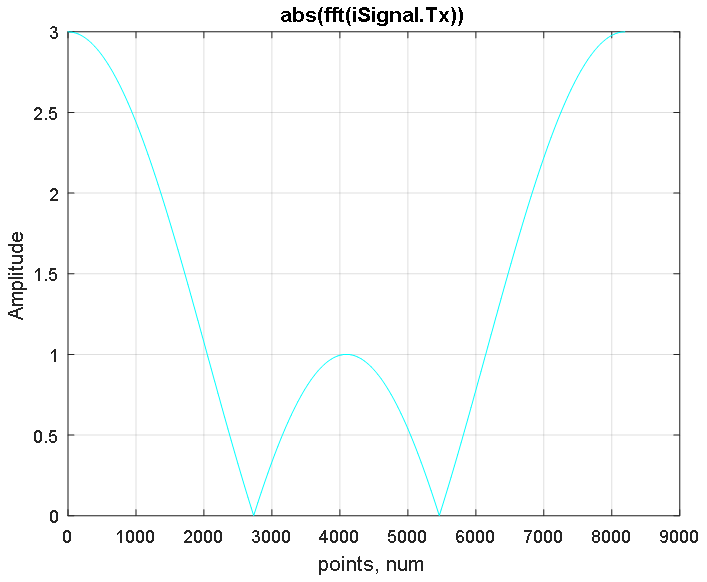Figura 3. Resposta em amplitude do espectro alterado do sinal iSignal.Tx obtido usando a FFT.
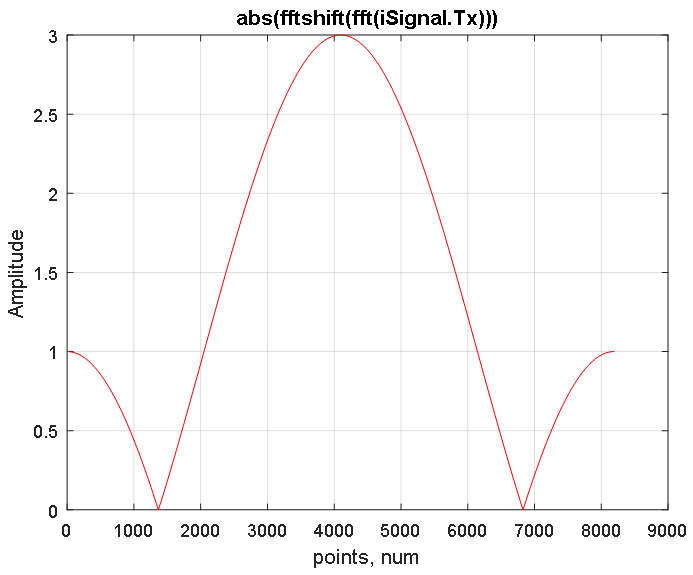Figura 4. Resposta em amplitude do espectro reconstruído do sinal iSignal.Tx mostrado na Figura 3. 2 ^ 13 amostras são apresentadas. A contagem média em 4097 corresponde à frequência zero. As frequências negativas estão localizadas no lado esquerdo (de 1 a 4096 pontos) e a região de frequências positivas no lado direito (de 4098 a 8192 pontos).Função de transferência do filtro passa-baixas normalizado
Neste exemplo, a função de transferência do filtro de segunda ordem tem a forma
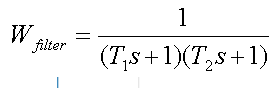
onde T1 e T2 são constantes de tempo do filtro. As frequências 1 / T1 são iguais e 1 / T2 são definidas em relação à frequência na qual os dados são transmitidos: 1 / T1 = 1 / T2 = 0,75 * bps (bps = 10,3125 Gbit / s).
Largura de banda de filtro normalizada
f_nrm =fmax/bps/points.*(-points/2:points/2-1).
Operador
s = f_nrm .* j;
A característica de fase de amplitude do filtro normalizado para frequências positivas e negativas normalizadas em relação à frequência de transmissão de sinal é mostrada na Figura 5. A característica de frequência de amplitude logarítmica do filtro é mostrada na Figura 6.
Figura 5. A característica da fase de amplitude de um filtro normalizado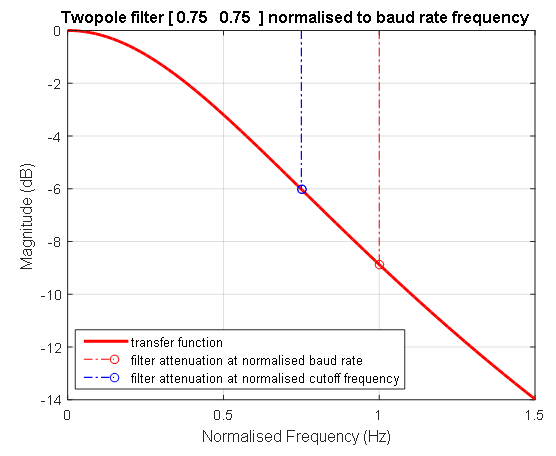
Figura 6. Resposta de frequência logarítmica em fase de amplitude de um filtro normalizado. A linha tracejada azul mostra a posição da frequência do filtro com um valor de 0,75 da frequência na qual os dados estão sendo transmitidos. Nesta frequência (1 / T1 = 1 / T2), o coeficiente de transmissão do filtro de segunda ordem é de -6 decibéis. A linha tracejada vermelha indica a frequência da unidade na qual os dados estão sendo transmitidos.Conversão dos resultados da medição da linha de sinal no tipo de função de transferência
A característica de fase de amplitude medida da linha de sinal inclui 1599 amostras na banda de até 20 GHz com um passo fixo de 12,475 MHz. Ele contém os seguintes valores de frequência: channel.f = 0.006495: 0.0012475: 20 GHz. Inicialmente, a linha de sinal era representada por uma característica de quatro terminais. Essa característica foi transformada e é usada no exemplo como uma função complexa unidimensional.
As frequências características da linha de sinal obtidas como resultado da medição não coincidem com as frequências do espectro do sinal de entrada que são múltiplos da frequência de transmissão de dados. Além disso, o espectro da linha de sinal contém apenas frequências positivas e não contém frequências na região zero. O espectro do sinal de entrada contém frequências positiva, zero e negativa.
Para converter as características da linha de sinal em uma função de transferência - uma característica cujas frequências coincidem com as frequências do espectro do sinal de entrada, são executados os seguintes passos.
1. O cálculo da amplitude das características da linha na frequência zero extrapolando-a. Para isso, a partir dos dez pontos da característica de amplitude mais próximos da frequência zero, são encontrados os coeficientes de um polinômio linear que se aproximam da característica de amplitude:
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);
O segundo coeficiente polinomial encontrado é igual à amplitude da característica na frequência zero:
channel.dc = a(2);
2. A resposta de fase na frequência zero é igual a zero.
channel.dcPhase = 0.00;
3. O recálculo das características do canal de amplitude.abs e do canal de fase.phase da linha de sinal com valores na frequência zero é realizado na frequência do espectro do sinal de entrada (f = -fmax / 2: fmax / pontos: fmax / 2-fmax / pontos) com extrapolação do área de zero e frequências negativas:
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);
A função de transferência obtida - a resposta de frequência em fase de amplitude do canal na região de baixa frequência é mostrada na Figura 7. As características de frequência de amplitude da linha de sinal medida e a função de transferência calculada em todas as faixas de frequência são mostradas na Figura 8. As mesmas características no espaço de fase são mostradas na Figura 9.
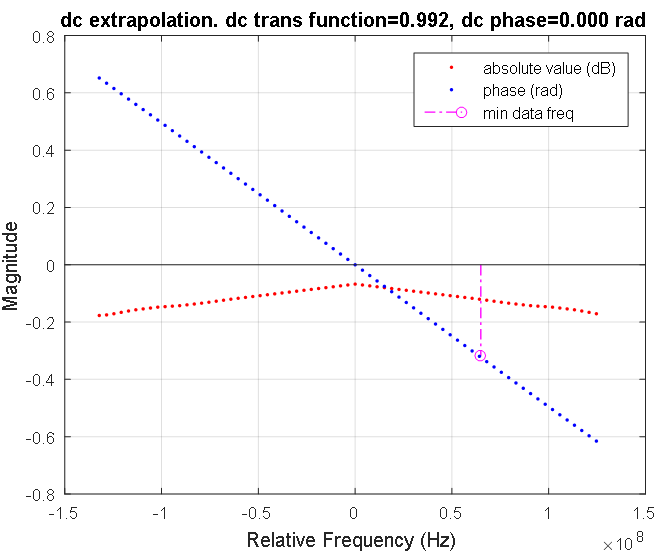Figura 7. A função de transferência da linha de sinal na região de baixa frequência. Pontos vermelhos e azuis indicam amplitude discreta e características de fase, respectivamente. A resposta de amplitude é mostrada em decibéis, a fase em radianos. A linha rosa marca a frequência mais baixa da característica medida da linha de sinal. O coeficiente de transmissão na frequência zero é 0,992.
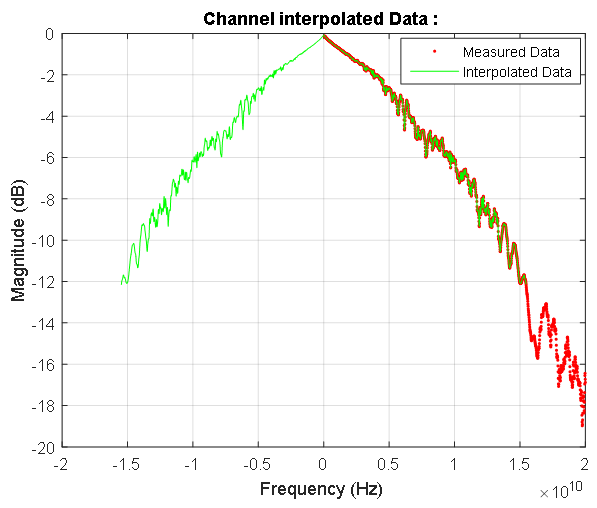Figura 8. Resposta em frequência da linha de sinal. Pontos azuis indicam os dados complexos da linha medida. A dependência simétrica calculada do ganho da linha de sinal nas frequências do espectro do sinal de entrada é destacada em vermelho. Na região de frequência zero, essa característica é mostrada na Figura 7.
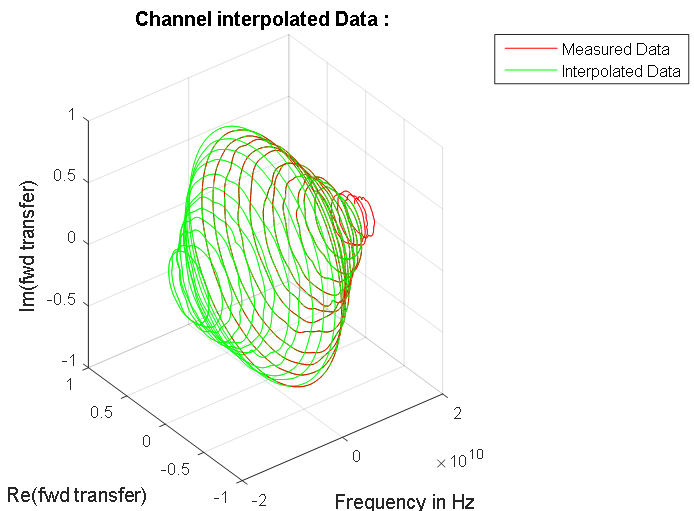Figura 9. Características de frequência da fase de amplitude da linha de dados medida e seu espectro normalizado.Cálculo da resposta do sinal
A resposta (resposta ao efeito de entrada) no domínio da frequência é obtida multiplicando o espectro do sinal pelo produto das funções de transferência dos elementos que relacionam a reação ao sinal de entrada. No nosso caso, o sinal passa pelo filtro e pela linha de sinal.
O ifft de transformação inversa de Fourier é usado para transferir o sinal do domínio da frequência para o domínio do tempo.
A saída do filtro no domínio de tempo iSignal.Filter_out é calculada como
TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));
O sinal de saída da linha iSignal.Rx é igual ao produto do espectro do sinal de entrada e das funções de transferência do filtro e da linha de sinal com a subsequente transferência do sinal recebido do domínio da frequência para o domínio do tempo.
TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));
A resposta do filtro ao pulso ideal de entrada e a resposta do canal são mostradas na Figura 10.
Figura 10. Saída do filtro (gráfico vermelho) e saída da linha de dados (gráfico verde). Sinal de entrada do filtro - um único pulso é mostrado na Figura 2. A entrada da linha de sinal é o sinal de saída do filtro.Aplicação. Código m usado MATLAB
Lista bibliográfica
1. IEEE802.3ap. Resultados da simulação NRZ de 10.3125Gbps usando "StatEye" e "Modelo de sinal para interferência" em componentes de canal em cascata. Shannon Sawyer e Charles Moore / Agilent Technologies. 24 janeiro de 2005
www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf2. O que é StatEye. Força-Tarefa IEEE 803.3ap. 16 de setembro de 2004
www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf3. Acordo Stat Eye / IBM. Steve Anderson. Xilinx, Inc.
www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf