Treinamento GAN em Sustentabilidade

A ideia da GAN foi publicada pela primeira vez por Jan Goodfellow Generative Adversarial Nets, Goodfellow et al. 2014 , após o qual as GANs são um dos melhores modelos generativos.

Como em qualquer outro modelo generativo, a tarefa da GAN é construir um modelo de dados e, mais especificamente, aprender a gerar amostras de uma distribuição o mais próximo possível da distribuição de dados (geralmente há um conjunto de dados de tamanho limitado no qual queremos modelar a distribuição de dados).

Os GANs têm um grande número de vantagens, mas têm uma desvantagem significativa: são muito difíceis de treinar.

Recentemente, vários trabalhos sobre sustentabilidade da GAN foram lançados:

• A otimização do GAN de descida de gradiente é localmente estável, Vaishnavh Nagarajan, J. Zico Kolter, 2017
• Os Numéricos de GANs, Lars Mescheder et al, 2017

Inspirado pelas idéias deles, fiz uma pequena pesquisa.

Tentei tornar o texto o mais simples possível e, se possível, usar apenas a matemática mais simples. Infelizmente, para justificar por que podemos considerar as propriedades dos campos vetoriais bidimensionais, precisamos cavar um pouco na direção do cálculo das variações. Mas se alguém não estiver familiarizado com esses termos, você poderá prosseguir com segurança imediatamente para a consideração de campos vetoriais bidimensionais para diferentes tipos de GAN.

Agora, tentaremos analisar os detalhes do procedimento de treinamento e entender o que está acontecendo lá.

GAN, o principal problema

Os GANs consistem em duas redes neurais: um discriminador e um gerador. Gerador - permite que você colete amostras de alguma distribuição (geralmente chamada de distribuição do gerador). O discriminador recebe amostras de entrada do conjunto de dados e gerador originais e aprende a prever de onde vem essa amostra (conjunto de dados ou gerador).

Esquema GAN:



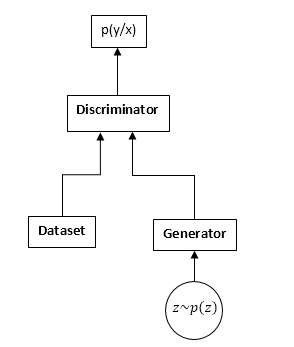
O processo de treinamento da GAN é o seguinte:

1. Nós coletamos n amostras do conjunto de dados e m amostras do gerador.
2. Fixamos os pesos do gerador e atualizamos os parâmetros discriminadores. Esta é uma tarefa de classificação comum. Só não precisamos treinar o discriminador até a convergência. E ainda mais frequentemente também interfere.
3. Fixamos os pesos do discriminador e atualizamos os pesos do gerador, para que o discriminador comece a pensar que nossas amostras são do conjunto de dados e não do gerador.
4. Repetimos 1-3, até que o discriminador e o gerador entrem em equilíbrio (isto é, nenhum dos outros pode "enganar" o outro).

Não examinaremos detalhadamente o processo de aprendizado da GAN. Na Internet, e no hubr em particular, existem muitos artigos explicando esse processo em detalhes.

Estaremos interessados ​​em algo completamente diferente. Ou seja, devido ao fato de estarmos competindo com duas redes neurais, a tarefa deixa de ser uma busca por um mínimo (máximo), mas transforma em casos particulares uma busca por um ponto de sela (ou seja, nas etapas 2 e 3, tentamos a mesma funcionalidade). maximizar por parâmetros discriminadores e minimizar por parâmetros do gerador), e nas etapas mais gerais 2 e 3 podemos otimizar funcionais completamente diferentes. Obviamente, o problema do minimax é um caso especial de otimização de diferentes funcionais - um funcional é tomado com sinais diferentes.

Vejamos isso nas fórmulas. Assumimos que pd (x) é a distribuição de onde o conjunto de dados é amostrado, pg (x) é a distribuição do gerador, D (x) é a saída do discriminador.

Ao treinar um discriminador, geralmente maximizamos essa funcionalidade:

$$

$$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$

Vetor de gradientes:

$$

$$v = \ \ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ theta D (x) \ dx \ + \ \ int {\ frac {p_g (x )} {1 \ - \ D (x)} \ nabla_ \ theta D (x) dx}}$$

Ao treinar o gerador, maximizamos:

$$

$$I \ = \ - \ int {p_g (x) log (1 \ - \ D (x)) dx}$$

O vetor de gradientes neste caso:

$$

$$u \ = \ \ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) log (1 \ - \ D (x)) dx}$$

No futuro, veremos que os funcionais podem ser substituídos respectivamente por:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Onde $$$f_1, f_2, f_3$ são selecionados de acordo com certas regras. Aliás, Ian Goodfellow usa em seu artigo original $$$f_1 e f_2$ como no treinamento de um discriminador regular, e $$$f_3$ escolhe para melhorar gradientes na fase inicial do treinamento:

$$

$$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ esquerda (x \ direita) = log \ esquerda (x \ direita)$$

À primeira vista, a tarefa pareceria muito semelhante à tarefa usual de aprender com descida de gradiente (subida). Por que, então, todos que se depararam com o treinamento da GAN concordaram que era tão difícil?

A resposta está na estrutura do campo vetorial, que usamos para atualizar os parâmetros das redes neurais. No caso do problema de classificação usual, usamos apenas o vetor gradiente, ou seja, o campo é potencial (a própria funcionalidade otimizada é o potencial desse campo vetorial). E os campos vetoriais em potencial têm algumas propriedades notáveis, uma das quais é a ausência de curvas fechadas. Ou seja, é impossível andar em círculos neste campo. Porém, ao treinar GAN, apesar do fato de que os campos vetoriais para o gerador e o discriminador são potencialmente separados (o mesmo é gradiente), o campo vetorial total não será potencial. E isso significa que nesse campo pode haver curvas fechadas, ou seja, podemos andar em círculos. E isso é muito, muito ruim.

Surge a pergunta: por que, mesmo assim, conseguimos treinar o GAN com bastante sucesso, talvez o campo ainda seja irrotacional (potencial)? E se sim, então por que é tão complicado?
Seguirei em frente, infelizmente o campo não é potencial, mas possui várias boas propriedades. Infelizmente, o campo também é muito sensível à parametrização de redes neurais (escolha de funções de ativação, uso de DropOut, BatchNormalization, etc.). Mas as primeiras coisas primeiro.

Campo GAN "Gradiente"

Consideraremos as funcionalidades de aprendizado da GAN da forma mais geral:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Precisamos otimizar ambas as funcionalidades ao mesmo tempo. Supondo que D (x) e pg (x) são funções absolutamente flexíveis, ou seja, podemos pegar qualquer número a qualquer momento, independentemente de outros pontos. Esse é um fato bem conhecido do cálculo das variações - você precisa alterar a função na direção da derivada variacional desse funcional (em geral, um análogo completo do aumento do gradiente).

Escrevemos a derivada variacional:

$$

$$\ frac {\ parcial J} {\ parcial D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ parcial I} {\ parcial p_g (x)} = f_3 (D (x))$$

Consideraremos apenas o primeiro funcional (para o discriminador), para o segundo tudo será o mesmo.

Mas, considerando que, de fato, podemos alterar a função apenas no conjunto de funções representáveis ​​pela nossa rede neural, escreveremos:

$$$$ exibição $$ ∆D (x) = \ frac {\ parcial D (x)} {\ parcial θ_j} Δθ_j $$ exibição $$

alterações nos parâmetros da rede, em geral, a descida normal do gradiente (aumento):

$$$$ display $$ ∆θj = \ frac {\ parcial J} {\ parcial θ_j} μ $$ display $$

µ é a taxa de aprendizado. Bem, a derivada em relação aos parâmetros de rede:

$$

$$\ frac {\ parcial J} {\ parcial \ theta_j} = \ int {\ frac {\ parcial J} {\ parcial D (y)} \ frac {\ parcial D (y)} {\ parcial \ theta_j} dy }$$

E agora estamos juntando tudo:

$$

$$∆D (x) = \ sum_ {j} {\ frac {\ parcial D (x)} {\ parcial \ theta_j} \ int {\ frac {\ parcial J} {\ parcial D (y)} \ frac { \ parcial D (y)} {\ parcial \ theta_j} aa} \ mu \ = \ mu \ int \ frac {\ parcial J} {\ parcial D (y)}} \ sum_ {j} {\ frac {\ parcial D (x)} {\ parcial \ theta_j} \ frac {\ parcial D (x)} {\ parcial \ theta_j} dy \ = \} \ mu \ int {\ frac {\ parcial J} {\ parcial D (y )} K_ \ theta (x, y) dy}$$

Onde: $$$K_ \ theta (x, y) \ = \ sum_ {j} {\ frac {\ parcial D (x)} {\ parcial \ theta_j} \ frac {\ parcial D (x)} {\ parcial \ theta_j} \ }$

Eu nunca vi esse recurso na literatura sobre aprendizado de máquina, por isso vou chamá-lo de núcleo paramétrico do sistema.

Bem, ou se formos a passos contínuos no tempo (das equações das diferenças às diferenciais), obtemos:

$$

$$\ frac {d} {dt} D (x) \ = \ \ int {\ frac {\ parcial J} {\ parcial D (y)} K_ \ theta (x, y) dy}$$

Esta equação mostra a relação interna do campo original (ponto a ponto para o discriminador) e a parametrização da rede neural. Obtemos uma equação completamente semelhante para o gerador.

Dado que K (x, y) (o núcleo paramétrico) é uma função definida positiva (bem, como pode ser representado como um produto escalar de gradientes nos pontos correspondentes), podemos concluir que quaisquer alterações nas funções treinadas (discriminador e gerador) pertencem ao espaço de Hilbert gerado pelo núcleo, ou seja, K (x, y). Gostaria de saber se é possível obter resultados significativos aqui. Mas ainda não olharemos nessa direção, mas olharemos na outra.

Como você pode ver, a estabilidade do GAN é determinada por dois componentes: as derivadas variacionais dos funcionais e a parametrização da rede neural. Nossa tarefa é ver como esse campo se comporta de maneira pontual, ou seja, se nossa rede pode representar absolutamente qualquer função. A tarefa se transforma em uma análise de um campo vetorial bidimensional. E isso, penso eu, está ao nosso alcance.

Sustentabilidade

Portanto, consideramos o seguinte campo vetorial:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ parcial J} {\ parcial D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ parcial I} {\ parcial p_g (x)}$$

Obviamente, essas equações podem ser consideradas por apenas um ponto x, levando em consideração a aparência de nossas derivadas variacionais:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

O primeiro requisito para esse sistema de equações é que o lado direito deve ir para 0 quando:
$$$p_d = p_g$

Caso contrário, tentaremos treinar o modelo, que obviamente não convergirá para a solução correta. I.e. D deve ser uma solução para a seguinte equação:

$$

$$f_1 ^ \ prime (D) \ + \ f_2 ^ \ prime (D) \ = \ 0$$

Denotamos essa solução como $$$D0$ .

Dado o fato de que pg (x) é a densidade de probabilidade do lado direito, podemos adicionar qualquer número sem violar as derivadas. Para fornecer 0 do lado direito no ponto desejado, subtraia o valor em t. $$$D0$ (isso deve ser feito se quisermos considerar pg em sentido horário - a transição de um campo parametrizado por densidades de probabilidade para campos livres).

Como resultado, obtemos o seguinte campo:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

A partir de agora, estudaremos os pontos de inatividade e a estabilidade dos campos desse tipo.
Podemos estudar dois tipos de estabilidade: local (na vizinhança do ponto de repouso) e global (usando o método da função Lyapunov).

Para estudar a estabilidade local, é necessário calcular a matriz de Jacobi do campo.
Para que o campo seja localmente "estável", é necessário que os autovalores tenham uma parte real negativa.

Diferentes tipos de GAN

1. Classic GAN

   
   
   No GAN clássico, usamos logloss regular:
   

   $$

   $$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$
   
   Para o treinamento do discriminador, é necessário maximizá-lo e, para o gerador, minimizá-lo. Nesse caso, o campo ficará assim:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + \ log (\ frac {1} {2})$$
   
   Vamos ver como os parâmetros (pg e D) evoluirão neste campo. Para fazer isso, use este script Python simples:
   
   
   Script

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Para ponto de partida $$$p_g = 0,9, D = 0,25$ ficará assim:
   
   
   
   O ponto de descanso desse campo será: pg = pd e D = 0,5
   
   Pode-se verificar facilmente que as partes reais dos autovalores da matriz de Jacobi são negativas, ou seja, o campo é localmente estável.
   Não vamos lidar com a prova da sustentabilidade global. Mas, se for muito interessante, você pode brincar com o script Python e garantir que o campo seja estável para quaisquer valores iniciais válidos.

2. Modificação por Jan Goodfellow

   
   Já discutimos acima que Ian Goodfellow no artigo original usou uma versão ligeiramente modificada do GAN. Para sua versão, as funções foram as seguintes:
   

   $$

   $$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ esquerda (x \ direita) = log \ esquerda (x \ direita)$$
   
   O campo ficará assim:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   O script python será o mesmo, apenas a função de campo é diferente:
   
   
   Script

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   E com os mesmos dados iniciais, a imagem fica assim:
   
   
   
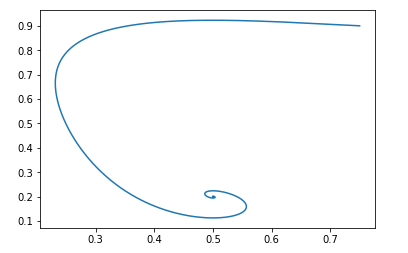
   E, novamente, é fácil verificar se o campo estará localmente estável.
   Ou seja, do ponto de vista da convergência, essa modificação não prejudica as propriedades do GAN, mas tem suas próprias vantagens em termos de treinamento de redes neurais.

3. Wasserstein gan

   
   Vejamos outra visão popular da GAN. A funcionalidade otimizada fica assim:
   

   $$

   $$J \ = \ \ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   Onde D pertence à classe das funções 1-Lipschitz em relação a x.
   Queremos maximizá-lo por D e minimizá-lo em pág.
   
   Obviamente, neste caso: $$$f_1 \ left (x \ right) = x, \ f_2 \ left (x \ right) = - x, \ f_3 \ left (x \ right) = x$
   
   E o campo ficará assim:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   Nesse campo, um círculo com um centro em um ponto é facilmente adivinhado. $$$p_g = p_d, D = 0$ .
   Ou seja, se formos nesse campo, sempre andaremos em círculos.
   
   Aqui está um exemplo de uma trajetória em tal campo:
   
   
   
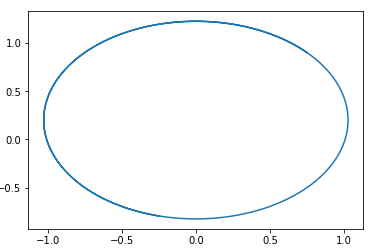
   A questão é: por que, então, acaba treinando esse tipo de GAN? A resposta é muito simples - essa análise não leva em conta o fato da propriedade 1-Lipschitz de D. Ou seja, não podemos assumir funções arbitrárias. A propósito, isso está de acordo com os resultados dos autores ... do artigo. Para evitar andar em círculo, eles recomendam treinar o discriminador para convergir: Wasserstein GAN

4. Novas opções de GAN

   
   Seleção de Recursos $$$f_1, f_2 e f_3$ Você pode criar diferentes opções de GAN. O principal requisito para essas funções é garantir a presença de um ponto de repouso "correto" e a estabilidade desse ponto (de preferência global, mas pelo menos local). Dou ao leitor a oportunidade de derivar as restrições sobre as funções f1, f2 e f3, necessárias para a estabilidade local. É fácil - basta considerar a equação quadrática para os autovalores da matriz de Jacobi.
   
   Vou dar um exemplo desse GAN:
   

   $$

   $$f_1 (x) \ = \ -0.5x ^ 2, \ f_2 (x) \ = \ x, \ f_3 (x) \ = \ -x$$
   
   Novamente, sugiro que o próprio leitor construa o campo desse GAN e prove sua estabilidade. (A propósito, este é um dos poucos campos para os quais a evidência de estabilidade global é fundamental - basta selecionar a função Lyapunov, a distância até o ponto de repouso). Basta levar em consideração que o ponto de descanso é D = 1.

Conclusão e pesquisas adicionais

Pode-se observar pela análise acima que todos os GANs clássicos (com exceção do GAN Wassertein, que possui métodos próprios para melhorar a estabilidade) possuem campos "bons". I.e. após esses campos, há um único ponto de repouso no qual a distribuição do gerador é igual à distribuição dos dados.

Por que, então, treinar GAN é uma tarefa tão difícil. A resposta é simples - parametrização de redes neurais. Com uma parametrização “ruim”, também podemos fazer caminhadas em círculos. Por exemplo, minhas experiências mostram que, por exemplo, o uso de BatchNormalization em qualquer uma das redes transforma imediatamente o campo em fechado. E a ativação do Relu funciona melhor.

Infelizmente, no momento não existe uma maneira única de verificar teoricamente quais elementos da rede neural como mudar o campo. Será uma perspectiva investigar as propriedades do kernel paramétrico do sistema - $$$K_ \ theta (x, y)$ .

Eu também queria falar sobre maneiras de regularizar os campos GAN e dar uma olhada nisso da perspectiva dos campos bidimensionais. Considere os algoritmos de aprendizado por reforço a partir dessa perspectiva. E muito mais Mas, infelizmente, o artigo acabou sendo muito grande de qualquer maneira, e mais sobre isso em outra ocasião.