Redes neurais profundas levaram a um avanço em muitas tarefas de reconhecimento de imagem, como visão por computador e reconhecimento de voz. A rede neural convolucional é um dos tipos populares de redes neurais.
Basicamente, uma rede neural convolucional pode ser considerada uma rede neural que utiliza muitas cópias idênticas do mesmo neurônio. Isso permite que a rede tenha um número limitado de parâmetros ao computar modelos grandes.
 Rede neural convolucional 2D
Rede neural convolucional 2DEssa técnica com várias cópias do mesmo neurônio tem uma analogia próxima com a abstração de funções em matemática e ciências da computação. Durante a programação, a função é escrita uma vez e depois reutilizada, sem a necessidade de escrever o mesmo código várias vezes em locais diferentes, o que acelera a execução do programa e reduz o número de erros. Da mesma forma, uma rede neural convolucional, depois de treinar um neurônio, o usa em muitos lugares, o que facilita o treinamento do modelo e minimiza os erros.
A estrutura das redes neurais convolucionais
Suponha que seja dada uma tarefa na qual é necessário prever a partir do áudio se existe a voz de uma pessoa no arquivo de áudio.
Na entrada, obtemos amostras de áudio em diferentes momentos. As amostras são distribuídas uniformemente.

A maneira mais fácil de classificá-los com uma rede neural é conectar todas as amostras a uma camada totalmente conectada. Nesse caso, cada entrada é conectada a cada neurônio.
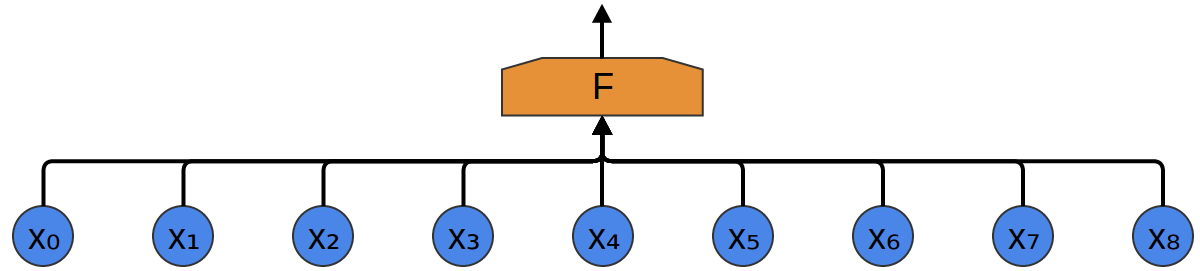
Uma abordagem mais complexa leva em conta alguma simetria nas propriedades que estão nos dados. Damos muita atenção às propriedades locais dos dados: qual é a frequência do som por um certo tempo? Aumentando ou diminuindo? E assim por diante
Levamos em conta as mesmas propriedades o tempo todo. É útil conhecer as frequências no início, meio e fim. Observe que essas são propriedades locais, pois você só precisa de uma pequena janela de sequência de áudio para defini-las.
Assim, é possível criar um grupo de neurônios A, que consideram pequenos segmentos de tempo em nossos dados. A analisa todos esses segmentos, calculando determinadas funções. Então, a saída dessa camada convolucional é alimentada em uma camada F. totalmente conectada.
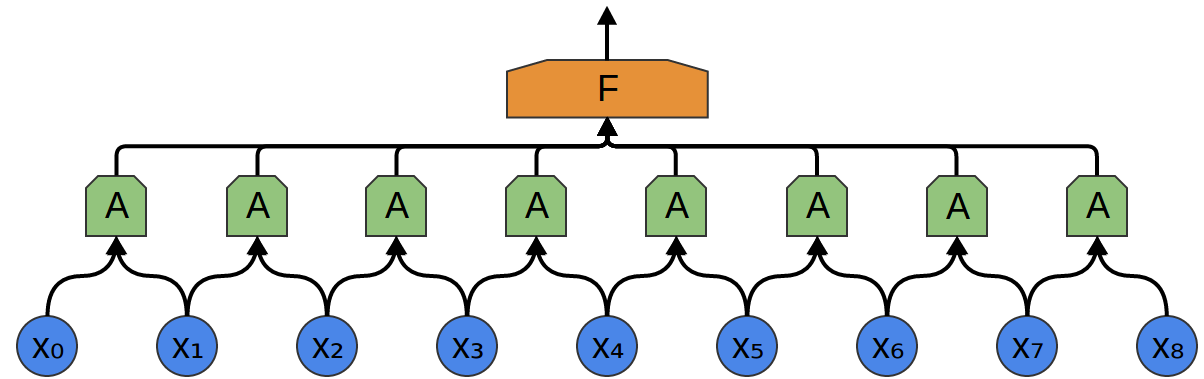
No exemplo acima, A processou apenas segmentos de dois pontos. Isso é raro na prática. Geralmente, a janela da camada de convolução é muito maior.
No exemplo a seguir, A recebe 3 segmentos na entrada. Isso também é improvável para tarefas do mundo real, mas, infelizmente, é difícil visualizar A conectando várias entradas.
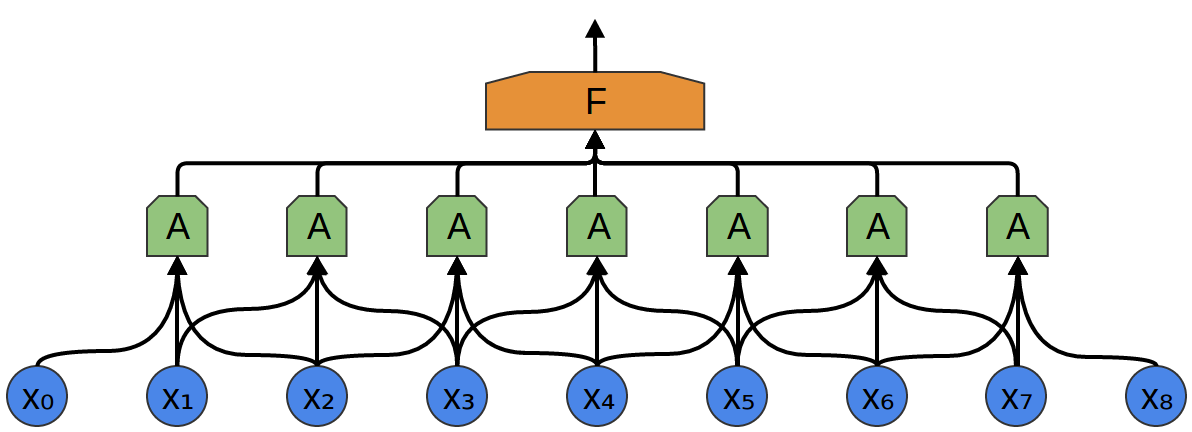
Uma boa propriedade das camadas convolucionais é que elas são compostas. Você pode alimentar a saída de uma camada convolucional para outra. Com cada camada, a rede descobre funções mais altas e abstratas.
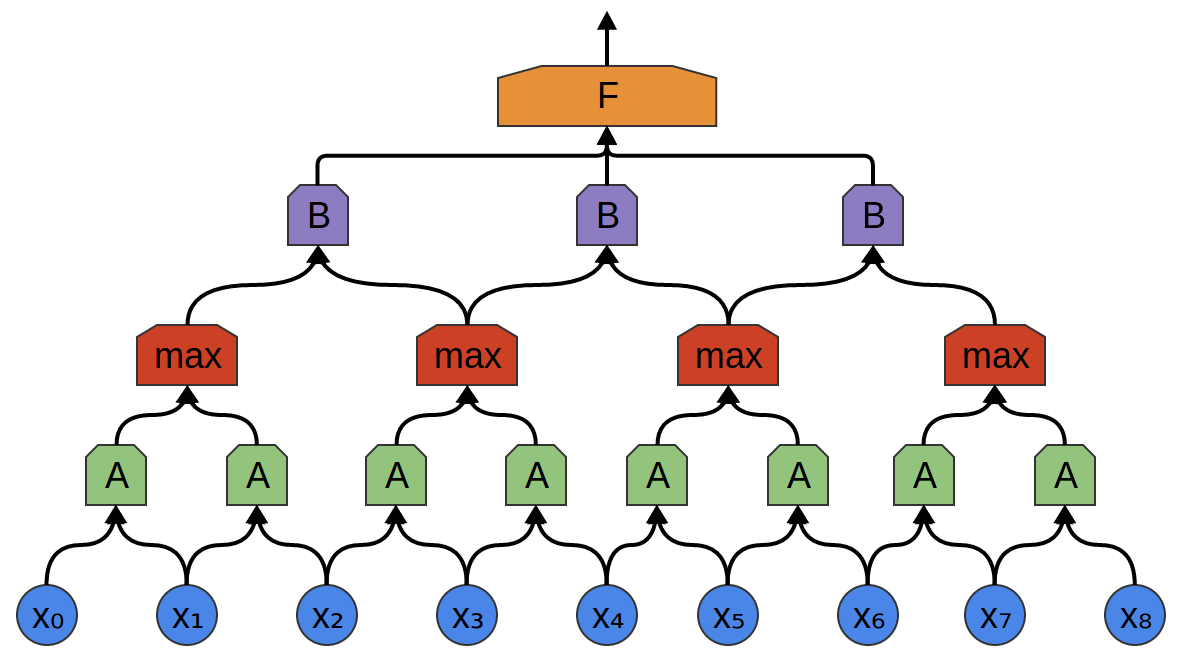
No exemplo a seguir, há um novo grupo de neurônios B. B é usado para criar outra camada convolucional colocada sobre a anterior.
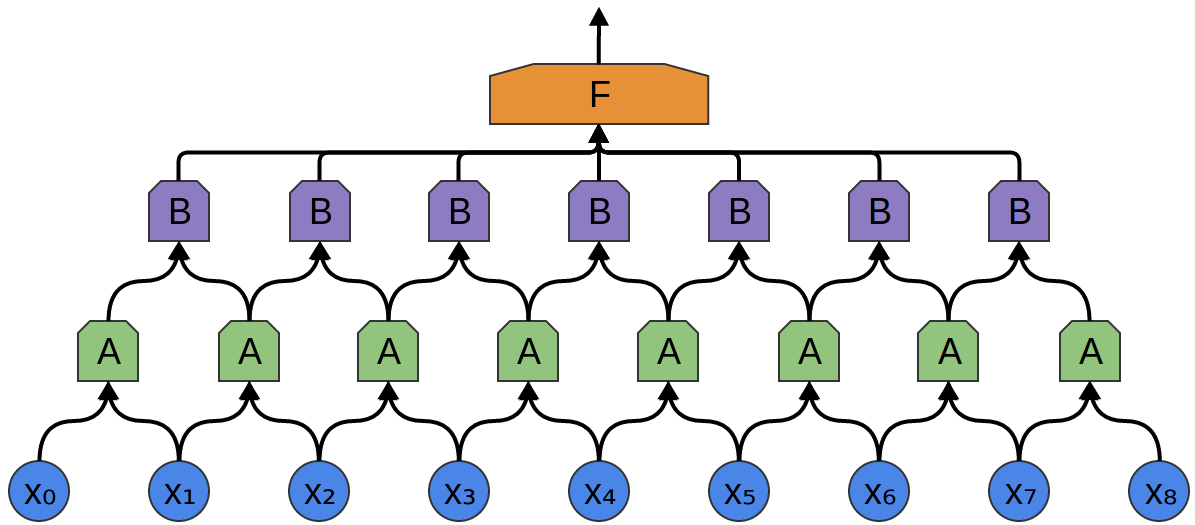
Camadas convolucionais são frequentemente interligadas por camadas combinadas. Em particular, existe um tipo de camada chamada max-pooling, que é extremamente popular.
Frequentemente, não nos importamos com o momento exato em que um sinal útil está presente nos dados. Se uma mudança na frequência do sinal ocorrer mais cedo ou mais tarde, isso importa?
O pool máximo absorve recursos máximos de pequenos blocos do nível anterior. A conclusão diz se o sinal da função desejada estava presente na camada anterior, mas não exatamente onde.
Camadas de pool máximo - essa é uma "diminuição". Ele permite que as camadas convolucionais posteriores trabalhem em grandes quantidades de dados, porque os pequenos patches após a camada de mesclagem correspondem ao patch muito maior à sua frente. Eles também nos tornam invariantes a algumas transformações de dados muito pequenas.
Nos exemplos anteriores, foram utilizadas camadas convolucionais unidimensionais. No entanto, as camadas convolucionais podem trabalhar com dados mais volumosos. De fato, as soluções mais famosas baseadas em redes neurais convolucionais usam redes neurais convolucionais bidimensionais para reconhecimento de padrões.
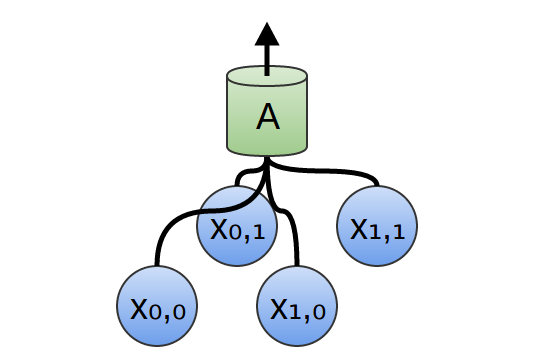
Em uma camada convolucional bidimensional, em vez de observar segmentos, A examinará os patches.
Para cada patch, A calculará a função. Por exemplo, ela pode aprender a detectar a presença de uma borda ou textura ou o contraste entre duas cores.
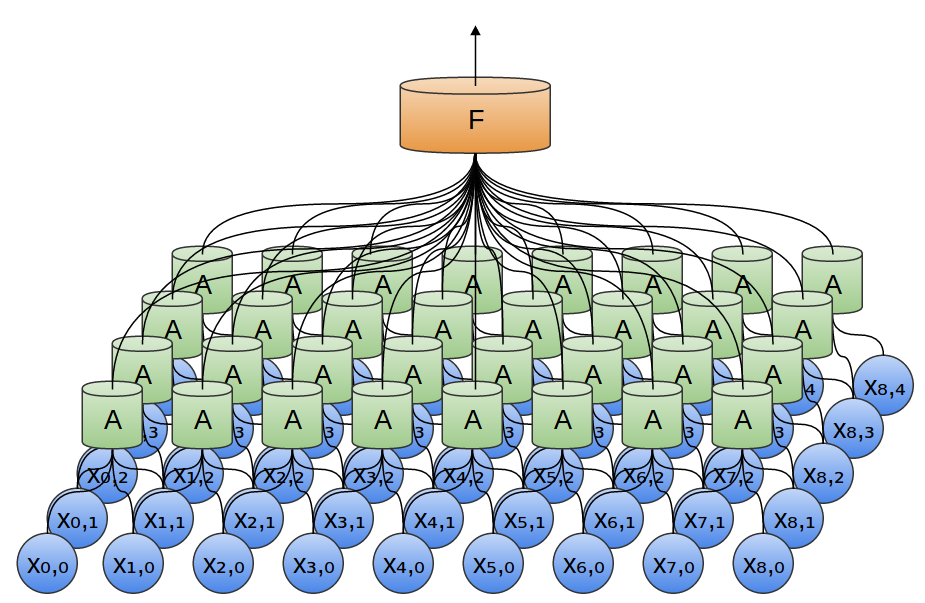
No exemplo anterior, a saída da camada convolucional foi alimentada em uma camada totalmente conectada. Porém, é possível compor duas camadas convolucionais, como foi o caso do caso unidimensional considerado.

Também podemos realizar o pool máximo em duas dimensões. Aqui tiramos o máximo de recursos de um pequeno patch.
Isso se resume ao fato de que, ao considerar toda a imagem, a posição exata da borda, até o pixel, não é importante. Basta saber onde está localizado em alguns pixels.
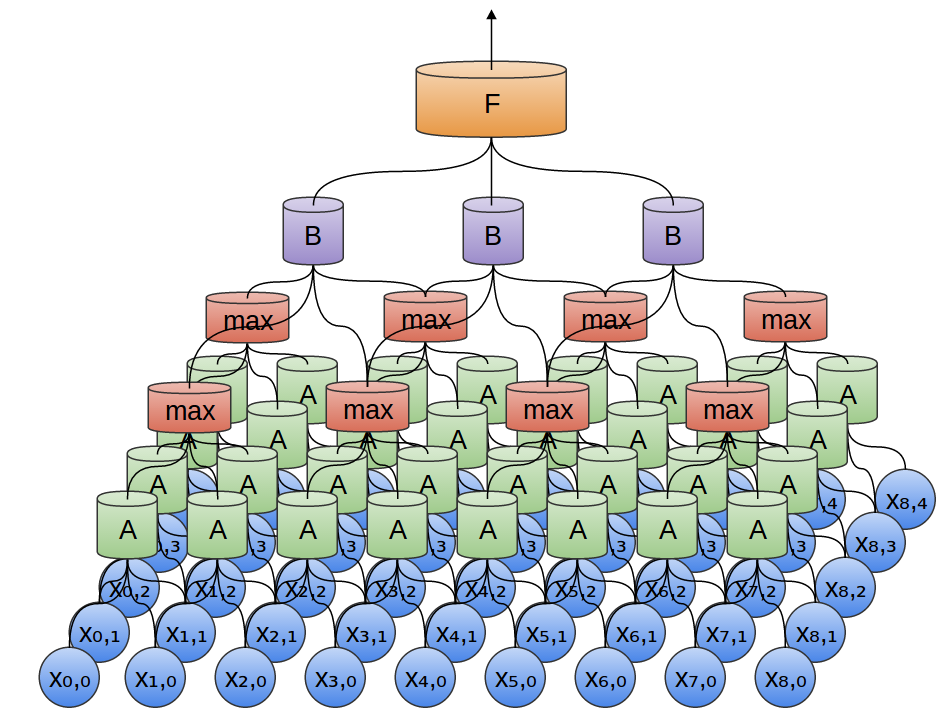
Além disso, às vezes, redes de convolução tridimensional são usadas para dados como vídeo ou dados em massa (por exemplo, digitalização 3D em medicina). No entanto, essas redes não são muito usadas e muito mais difíceis de visualizar.
Anteriormente, dissemos que A é um grupo de neurônios. Seremos mais precisos nisso: o que é A?
Nas camadas convolucionais tradicionais, A é um conjunto paralelo de neurônios, todos os neurônios recebem os mesmos sinais de entrada e calculam funções diferentes.
Por exemplo, em uma camada convolucional bidimensional, um neurônio pode detectar arestas horizontais, outro arestas verticais e uma terceira cor verde-vermelha.
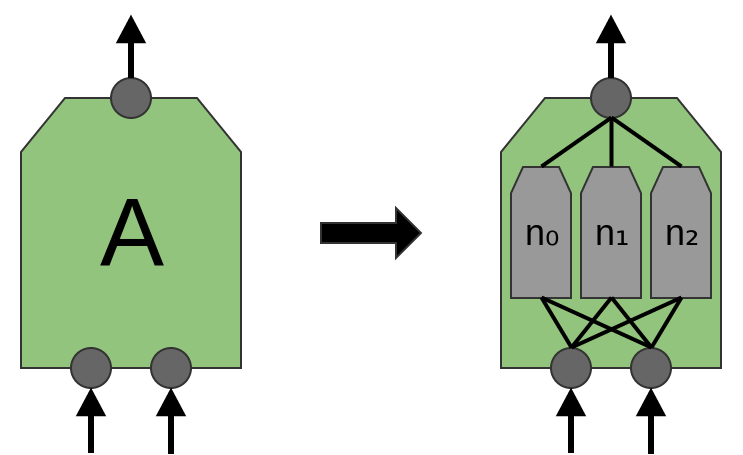
O artigo 'Rede em rede' (Lin et al. (2013)) propõe uma nova camada, “Mlpconv”. Nesse modelo, A possui vários níveis de neurônios, com a última camada derivando funções de nível superior para a região que está sendo tratada. No artigo, o modelo alcança resultados impressionantes, definindo um novo nível de tecnologia em vários conjuntos de dados de referência.
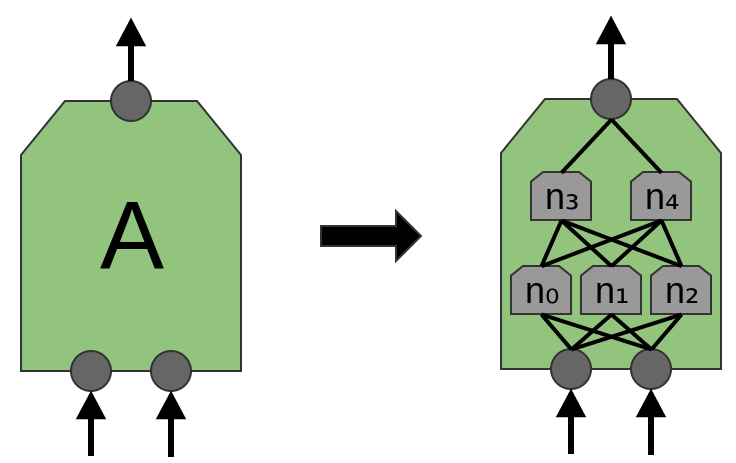
Para os fins desta publicação, focaremos nas camadas convolucionais padrão.
Resultados da Rede Neural Convolucional
Em 2012, Alex Krizhevsky, Ilya Sutskever e Geoff Hinton alcançaram uma melhoria significativa na qualidade do reconhecimento em comparação com as soluções conhecidas na época (Krizehvsky et al. (2012)).
O progresso foi o resultado da combinação de várias abordagens. Os processadores gráficos foram usados para treinar uma rede neural profunda (de acordo com os padrões de 2012). Um novo tipo de neurônio (ReLU) e uma nova técnica foram usadas para reduzir o problema chamado "super ajuste" (DropOut). Utilizamos um grande conjunto de dados com um grande número de categorias de imagens (ImageNet). E, claro, era uma rede neural convolucional.
A arquitetura mostrada abaixo era profunda. Possui 5 camadas convolucionais, 3 conjuntos alternados e três camadas totalmente conectadas.
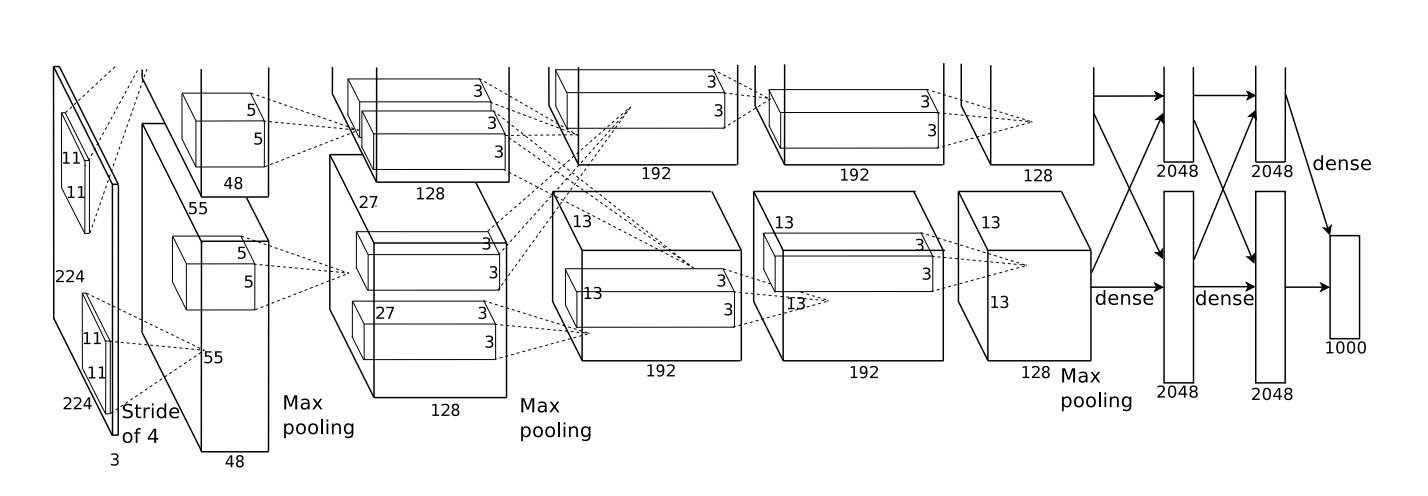
De Krizehvsky et al. (2012)
A rede foi treinada para classificar fotos em milhares de categorias diferentes.
O modelo de Krizhevsky et al. Foi capaz de dar a resposta correta em 63% dos casos. Além disso, a resposta correta das 5 melhores respostas, existem 85% das previsões!

Vamos ilustrar o que o primeiro nível da rede reconhece.
Lembre-se de que as camadas convolucionais foram divididas entre duas GPUs. As informações não vão e voltam através de cada camada. Acontece que toda vez que o modelo é iniciado, os dois lados se especializam.

Filtros obtidos pela primeira camada convolucional. A metade superior corresponde a uma camada em uma GPU e a metade inferior na outra. De Krizehvsky et al. (2012)
Os neurônios de um lado se concentram no preto e branco, aprendendo a detectar bordas de diferentes orientações e tamanhos. Os neurônios, por outro lado, são especializados em cores e texturas, detectam contrastes e padrões de cores. Lembre-se de que os neurônios são inicializados aleatoriamente. Nenhuma pessoa foi montá-los como detectores de fronteira ou dividi-los dessa maneira. Isso aconteceu durante o treinamento da rede de classificação de imagens.
Esses resultados notáveis (e outros resultados emocionantes ao longo do tempo) foram apenas o começo. Eles foram rapidamente seguidos por muitos outros trabalhos que testaram abordagens modificadas e melhoraram gradualmente os resultados ou os aplicaram em outras áreas.
As redes neurais convolucionais são uma ferramenta importante na visão computacional e no reconhecimento de padrões modernos.
Formalização de redes neurais convolucionais
Considere uma camada convolucional unidimensional com entradas {xn} e saídas {yn}:
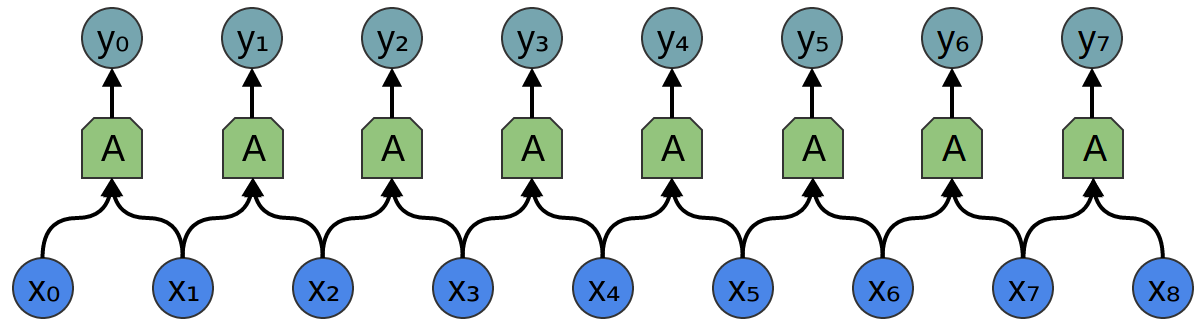
É relativamente fácil descrever os resultados em termos de entrada:
yn = A (x, x + 1, ...)
Por exemplo, no exemplo acima:
y0 = A (x0, x1)
y1 = A (x1, x2)
Da mesma forma, se considerarmos uma camada convolucional bidimensional com entradas {xn, m} e saídas {yn, m}:
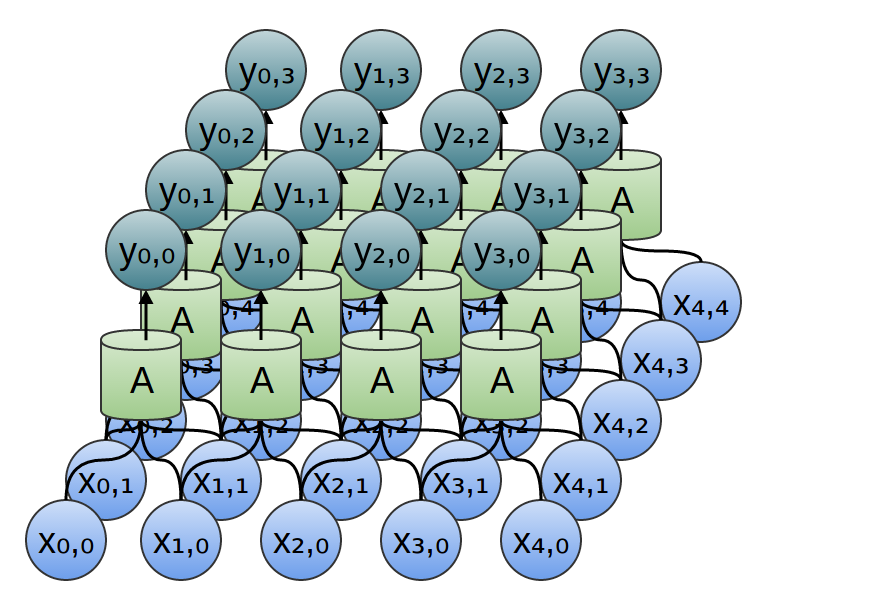
A rede pode ser representada por uma matriz bidimensional de valores.
Conclusão
A operação de convolução é uma ferramenta poderosa. Em matemática, a operação de convolução surge em diferentes contextos, desde o estudo de equações diferenciais parciais até a teoria das probabilidades. Em parte devido ao seu papel no PDE, a convolução é importante nas ciências físicas. A convolução também desempenha um papel importante em muitas áreas de aplicação, como gráficos de computador e processamento de sinais.