Por muitos anos eu assisto snooker como um esporte. Tem tudo: a beleza hipnotizante de um jogo intelectual, a elegância dos golpes de kiem e a tensão psicológica da competição. Mas há uma coisa que eu não gosto - o seu sistema de classificação .
Sua principal desvantagem é que ele leva em conta apenas o fato da conquista do torneio sem levar em conta a “complexidade” dos jogos. O modelo Elo é privado dessa desvantagem, que monitora a “força” dos jogadores e a atualiza dependendo dos resultados das partidas e da “força” do oponente. No entanto, ele não se encaixa perfeitamente: acredita-se que todos os jogos sejam realizados em condições iguais e, na sinuca, eles são jogados até um certo número de frames ganhos (festas). Para explicar esse fato, considerei outro modelo, que chamei de EloBeta .
Este artigo estuda a qualidade dos modelos Elo e EloBet com base nos resultados das partidas de sinuca. É importante observar que os principais objetivos são avaliar a "força" dos jogadores e criar uma classificação "justa", em vez de criar modelos preditivos para obter lucro.

A classificação atual do sinuca é baseada nas conquistas do jogador em torneios com seus diferentes "pesos". Era uma vez, apenas os Campeonatos do Mundo eram levados em consideração. Após o aparecimento de muitas outras competições, foi desenvolvida uma tabela de pontos que o jogador poderia ganhar quando atingisse uma determinada fase do torneio. Agora, a classificação tem a forma de uma quantia "móvel" de prêmio em dinheiro que o jogador ganhou durante os (aproximadamente) últimos dois anos civis.
Este sistema tem duas vantagens principais: é simples (ganhe muito dinheiro - suba no ranking) e previsível (se você quiser subir para um determinado lugar - ganhe uma certa quantia de dinheiro, todas as outras coisas sendo iguais). O problema é que, com esse método, a força (habilidade, forma) dos oponentes não é levada em consideração . O contra-argumento usual é: "Se um jogador chegou à fase final do torneio, ele é, por definição, o atual jogador forte" ("jogadores fracos não vencem torneios"). Parece bastante convincente. No entanto, na sinuca, como em qualquer esporte, o papel do caso deve ser levado em consideração: se um jogador é "mais fraco", isso não significa que ele / ela nunca poderá ganhar "mais forte" em uma partida contra um jogador. Isso acontece com menos frequência do que o cenário inverso. É aqui que o modelo Elo entra em cena.
A idéia do modelo Elo é que cada jogador esteja associado a uma classificação numérica. É introduzido um pressuposto de que o resultado de um jogo entre dois jogadores pode ser previsto com base na diferença em suas classificações: valores mais altos significam uma maior probabilidade de ganhar um jogador "forte" (com uma classificação mais alta). A classificação Elo é baseada na "força" atual , calculada com base nos resultados de partidas com outros jogadores. Isso evita uma falha importante no atual sistema de classificação oficial. Essa abordagem também permite que você atualize a classificação do jogador durante o torneio para responder numericamente ao seu bom desempenho.
Tendo experiência prática com a classificação Elo, parece-me que ele deve se mostrar bem na sinuca. No entanto, há um obstáculo: ele foi projetado para competições com um único tipo de partida . É claro que existem variações para levar em conta as vantagens do campo em casa no futebol e o primeiro passo no xadrez (ambos na forma de adicionar um número fixo de pontos de classificação ao jogador com vantagem). Na sinuca, as partidas são disputadas no formato "best of N": o jogador que vencer as primeiras vitórias n= fracN+12 quadros (festas). Também chamaremos esse formato "até n vitórias ".
Intuitivamente, vencer uma partida de até 10 vitórias (final de um torneio sério) deve ser mais difícil para um jogador "fraco" do que vencer uma partida de 4 vitórias (primeira rodada dos torneios atuais das Nações Unidas). Isso é levado em consideração no meu modelo EloBet .
A idéia de usar a classificação Elo no snooker não é de forma alguma nova. Por exemplo, existem os seguintes trabalhos:
- O Snooker Analyst usa um sistema de classificação "Elo like" (mais como um modelo de Bradley - Terry ). A idéia é atualizar a classificação com base na diferença entre o número "real" e "esperado" de quadros ganhos. Essa abordagem levanta questões. Obviamente, a maior diferença no número de quadros provavelmente demonstra a maior diferença na força, mas inicialmente o jogador não tem essa tarefa. Na sinuca, o objetivo é "apenas" vencer a partida, ou seja, Ganhe um certo número de frames antes do oponente.
- Esta discussão está no fórum com a implementação do modelo básico do Elo.
- Isso e esses são usos reais na sinuca amadora.
- Talvez haja outros trabalhos que eu perdi. Ficaria muito grato por qualquer informação sobre este tópico.
Revisão
Este artigo é destinado a usuários da língua R que estão interessados em estudar a classificação do Elo e para fãs de sinuca. Todas as experiências são escritas com a ideia de serem reproduzíveis. O código está oculto em spoilers, possui comentários e usa pacotes tidyverse , portanto, pode ser interessante para os usuários lerem por si só R. Supõe-se que todo o código apresentado seja executado sequencialmente. Um arquivo pode ser encontrado aqui .
O artigo está organizado da seguinte maneira:
- A seção Modelo descreve as abordagens do Elo e EloBet com implementação em R.
- A seção Experimento descreve os detalhes e a motivação do cálculo: quais dados e metodologia são usados (e por que) e quais resultados são obtidos.
- A seção Estudo de Classificação EloBet contém os resultados da aplicação do modelo EloBet a dados reais de sinuca. Ele estará mais interessado em amantes de sinuca.
Vamos precisar da seguinte inicialização.
Código de inicialização# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
Modelos
Ambos os modelos são baseados nas seguintes suposições:
- Existe um conjunto fixo de jogadores que devem ser classificados de "mais forte" (primeiro lugar) a "mais fraco" (último lugar).
- Classificação por associação de jogadores i com classificação numérica ri : Um número que representa a "força" do jogador (um valor mais alto significa um jogador mais forte).
- Quanto maior a diferença nas classificações antes da partida, menor a vitória do jogador "fraco" (com uma classificação mais baixa).
- As classificações são atualizadas após cada partida com base no resultado e nas classificações anteriores a ela.
- Uma vitória sobre um oponente "mais forte" deve ser acompanhada de um aumento maior na classificação do que uma vitória sobre um oponente "mais fraco". Com a derrota, o oposto é verdadeiro.
Elo
Código do modelo Elo #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
O Elo Model atualiza as classificações pelo seguinte procedimento:
Cálculo da probabilidade de um determinado jogador vencer a partida (antes de começar). A probabilidade de um jogador vencer (nós o chamaremos de "primeiro") com o identificador i e avaliado ri sobre outro jogador ("segundo") com identificador j e avaliado rj é igual a
Pr(ri,rj)= frac11+10(rj−ri)/400
Com essa abordagem, o cálculo da probabilidade obedece à terceira hipótese.
Normalizar a diferença para 400 é uma maneira matemática de dizer qual diferença é considerada "grande". Este número pode ser substituído por um parâmetro de modelo. xi No entanto, isso afeta apenas a disseminação de classificações futuras e geralmente é redundante. Um valor de 400 é bastante padrão.
Com uma abordagem geral, a probabilidade de vitória é igual a L(rj−ri) onde L(x) alguma função estritamente crescente com valores de 0 a 1. Usaremos a curva logística. Um estudo mais completo pode ser encontrado neste artigo .
Cálculo do resultado da partida S . No modelo base, é igual a 1 em caso de vitória do primeiro jogador (derrota do segundo), 0,5 em caso de empate e 0 em caso de derrota do primeiro jogador (vitória do segundo).
Atualização da classificação :
- delta=K cdot(S−Pr(ri,rj)) . Esse é o valor pelo qual as classificações serão alteradas. Ela usa um coeficiente K (o único parâmetro do modelo). Menos K (com probabilidades iguais) significa uma mudança menor nas classificações - o modelo é mais conservador, ou seja, são necessárias mais vitórias para "provar" uma mudança de força. Por outro lado, mais K significa mais credibilidade com resultados recentes do que as classificações atuais. A escolha de "ideal" K é uma maneira de criar um sistema de classificação "bom" .
- r(novo)i=ri+ delta , r(novo)j=rj− delta .
Observações :
- Como pode ser visto nas fórmulas de atualização, a soma das classificações de todos os jogadores considerados não muda com o tempo: a classificação aumenta devido a uma diminuição na classificação do oponente
- Jogadores sem partidas disputadas estão associados a uma classificação inicial de 0. Normalmente, valores de 1500 ou 1000 são usados, mas não vejo outra razão senão psicológica. Levando em conta a observação anterior, usar zero significa que a soma de todas as classificações é sempre zero, o que é bonito à sua maneira.
- É necessário jogar um certo número de partidas para que a classificação reflita a "força" do jogador. Isso apresenta um problema: jogadores recém-adicionados começam com uma classificação de 0, o que provavelmente não é o menor entre os jogadores atuais. Em outras palavras, os “novatos” são considerados “mais fortes” do que alguns outros jogadores. Você pode tentar combater isso com procedimentos externos de atualização de classificação ao entrar em um novo player.
Por que esse algoritmo faz sentido? Em caso de igualdade de classificação delta sempre é igual  . Suponha, por exemplo, que ri=0 e rj=400 . Isso significa que a probabilidade de ganhar o primeiro jogador é frac11+10 aproximadamente0,0909 , ou seja, ele / ela vencerá 1 jogo em 11.
. Suponha, por exemplo, que ri=0 e rj=400 . Isso significa que a probabilidade de ganhar o primeiro jogador é frac11+10 aproximadamente0,0909 , ou seja, ele / ela vencerá 1 jogo em 11.
- Em caso de vitória, ele / ela receberá um aumento de aproximadamente 0,909 cdotK , que é mais do que no caso da igualdade de classificações.
- Em caso de derrota, ele / ela receberá uma redução de aproximadamente 0,0909 cdotK , que é menor do que no caso de igualdade de classificações.
Isso mostra que o modelo Elo obedece à quinta suposição: a vitória sobre um oponente é "mais forte" é acompanhada por um aumento maior na classificação do que a vitória sobre um oponente é "mais fraca" e vice-versa.
Obviamente, o modelo Elo tem seus próprios recursos práticos (de alto nível). No entanto, o mais importante para o nosso estudo é o seguinte: pressupõe-se que todas as partidas sejam realizadas em pé de igualdade. Isso significa que a distância da partida não é levada em consideração: uma vitória em uma partida de até 4 vitórias é recompensada da mesma maneira que uma vitória em uma partida de até 10 vitórias. Aí vem o modelo de palco EloBeta.
EloBeta
Código do Modelo EloBet #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
No modelo Elo, a diferença nas classificações afeta diretamente a probabilidade de ganhar a partida inteira. A idéia principal do modelo EloBet é a influência direta da diferença nas classificações na probabilidade de ganhar em um quadro e no cálculo explícito da probabilidade de um jogador vencer n quadros antes do oponente .
A questão permanece: como calcular essa probabilidade? Acontece que este é um dos problemas mais antigos da história da teoria das probabilidades e tem seu próprio nome - o problema da divisão de apostas (Problema de pontos). Uma apresentação muito agradável pode ser encontrada neste artigo . Usando sua notação, a probabilidade desejada é:
P(n,n)= soma limites2n−1j=n2n−1 escolhajpj(1−p)2n−1−j
Aqui P(n,n) - probabilidade do primeiro jogador vencer a partida antes n vitórias; p - a probabilidade de sua vitória em um quadro (o oponente tem probabilidade  ) Com essa abordagem, supõe-se que os resultados do quadro na partida sejam independentes um do outro . Isso pode estar em dúvida, mas é uma suposição necessária para esse modelo.
) Com essa abordagem, supõe-se que os resultados do quadro na partida sejam independentes um do outro . Isso pode estar em dúvida, mas é uma suposição necessária para esse modelo.
Existe uma maneira mais rápida de calcular? Acontece que a resposta é sim. Após várias horas de conversão de fórmula, experimentos práticos e pesquisas na Internet, encontrei a seguinte propriedade em uma função beta incompleta regularizada Ix(a,b) . Substituindo m=k, n=2k−1 nesta propriedade e substituindo k em n acontece P(n,n)=Ip(n,n) .
Isso também é uma boa notícia para os usuários do R, pois Ip(n,n) pode ser calculado como pbeta(p, n, n) . Nota : o caso geral da probabilidade de vitória em n frames antes do adversário vencer m também pode ser calculado como Ip(n,m) e pbeta(p, n, m) respectivamente. Isso abre grandes oportunidades para atualizar a probabilidade de vitória durante a partida .
O procedimento de atualização de classificação na estrutura do modelo EloBet tem a seguinte forma (com classificações conhecidas ri e rj número de quadros necessários para ganhar n e o resultado da partida S , como no modelo Elo):
- Cálculo da probabilidade de vitória do primeiro jogador em um quadro : p=Pr(ri,rj)= frac11+10(rj−ri)/400 .
- Cálculo da probabilidade de vitória deste jogador na partida : PrBeta(ri,rj)=Ip(n,n) . Por exemplo, se p igual a 0,4, a probabilidade de vencer a partida antes de 4 vitórias cai para 0,29 e em "para 18 vitórias" - para 0,11.
- Atualização da classificação :
- delta=K cdot(S−PrBeta(ri,rj)) .
- r(novo)i=ri+ delta , r(novo)j=rj− delta .
Nota : porque a diferença nas classificações afeta diretamente a probabilidade de vitória em um quadro, e não em toda a partida, um valor do coeficiente ideal mais baixo deve ser esperado K : parte do valor delta vem de um efeito reforçador PrBeta(ri,rj) .
A idéia de calcular o resultado de uma partida com base na probabilidade de vitória em um quadro não é muito nova. Neste site de autoria da François Labelle , você pode encontrar um cálculo on-line da probabilidade de ganhar o "melhor N "Corresponder, juntamente com outras funções. Fiquei feliz em ver que nossos resultados de cálculo coincidem. No entanto, não encontrei nenhuma fonte para introduzir tal abordagem no procedimento de atualização para as classificações Elo. Como antes, ficarei muito grato por qualquer informação sobre este tópico.
Eu só consegui encontrar este artigo e a descrição do sistema Elo no servidor de gamão (FIBS). Há também um análogo em russo . Aqui, diferentes durações de correspondência são levadas em consideração multiplicando a diferença de classificações pela raiz quadrada da distância da correspondência. No entanto, parece não ter nenhuma justificativa teórica.
Um experimento
Um experimento tem vários objetivos. Com base nos resultados das partidas de sinuca:
- Determinar os melhores valores de coeficiente K para os dois modelos.
- Estudar a estabilidade dos modelos em termos da precisão da probabilidade preditiva.
- Estudar o efeito do uso de torneios de "convite" nas classificações.
- Crie um histórico de classificação justo para a temporada 2017/18 para todos os jogadores profissionais.
Dados
Código de geração de dados da experiência # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
Usaremos os dados do snooker do pacote comperank . A fonte original é snooker.org . Os resultados são obtidos das seguintes correspondências:
- A partida foi disputada na temporada 2016/17 ou 2017/18 .
- A partida faz parte de um torneio de sinuca "profissional" , ou seja:
- É do tipo "Invitational", "Qualifying" ou "Ranking". Também distinguiremos dois conjuntos de partidas: "todas as partidas" (de todos os dados do torneio) e "partidas oficiais" (excluindo torneios por convite). Há duas razões para isso:
- Nos torneios de convites, nem todos os jogadores têm a oportunidade de alterar sua classificação. Isso não é necessariamente ruim dentro da estrutura dos modelos Elo e EloBet, mas tem um "tom de injustiça".
- Há uma crença de que os jogadores “levam a sério” apenas para partidas oficiais de classificação. Nota : a maioria dos torneios por convite faz parte da Liga do Campeonato, que eu acho que é aceita pela maioria dos jogadores.
não muito a sério na forma de prática com a capacidade de ganhar dinheiro. A presença desses torneios pode afetar o ranking. Além da "Championship League", existem outros torneios de convites: "2016 China Championship", ambos "Champion of Champions", ambos "Masters", "2017 Hong Kong Masters", "2017 World Games", "2017 World Games", "2017 Romanian Masters".
- Descreve uma sinuca tradicional (não 6 vermelhos ou Power Snooker) entre jogadores individuais (não equipes).
- Ambos os sexos podem estar envolvidos (não apenas homens ou mulheres).
- Jogadores de todas as idades podem participar (não apenas idosos ou "menores de 21 anos").
- Este não é um "tiroteio" porque caso contrário, esses torneios são armazenados no banco de dados snooker.org.
- A partida realmente aconteceu : o resultado é o resultado de um jogo real envolvendo os dois jogadores.
- A partida é realizada entre dois profissionais . A lista de profissionais é retirada para a temporada 2017/18 (131 jogadores). Esta decisão parece ser a mais controversa, pois a remoção de partidas envolvendo "blinds" amadores e a derrota de profissionais amadores. Isso leva a uma vantagem injusta desses jogadores. Parece-me que tal decisão é necessária para reduzir a inflação de classificação que ocorrerá ao levar em consideração as correspondências com amadores. Outra abordagem é estudar profissionais e amadores juntos, mas isso parece irracional na estrutura deste estudo. A derrota de um amador profissional é considerada uma perda da oportunidade de aumentar a classificação.
O número final de partidas usadas é 4118 para "todas as partidas" e 3644 para "partidas oficiais" (62,9 e 55,6 por jogador, respectivamente).
Metodologia
Código da Função Experimental #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 . , . :
- K :
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 onde T — , |T| — , St — , Pt — ( ). , " " .
- K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
Resultados
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
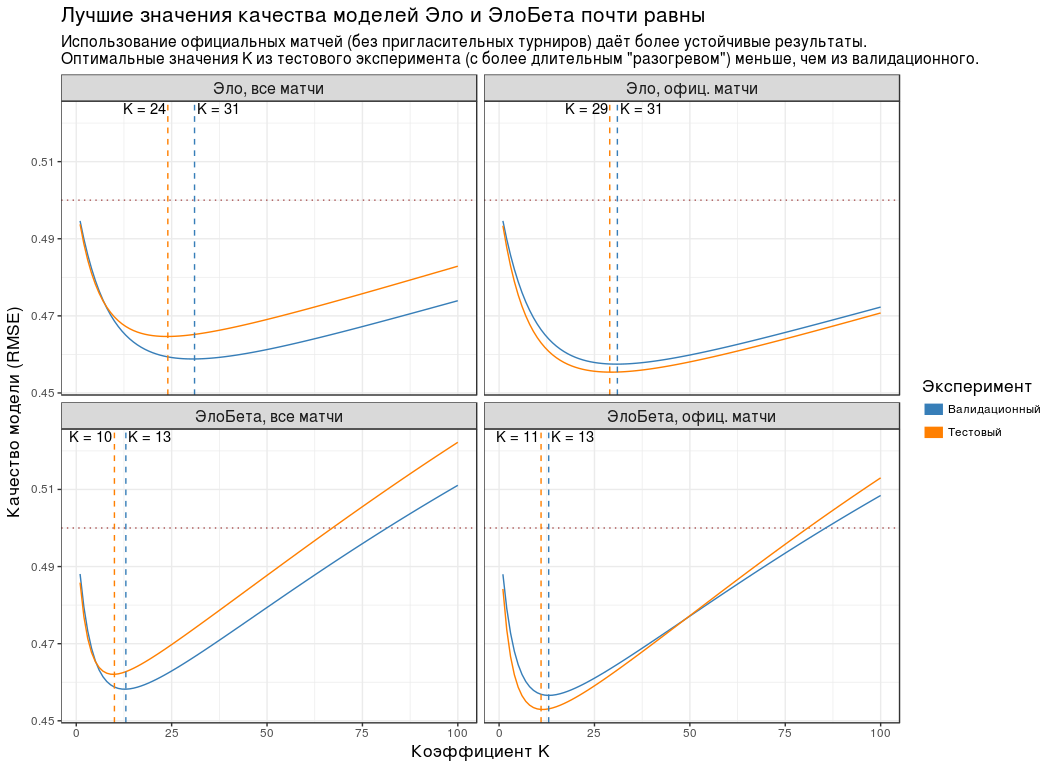
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | 29 | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
Porque , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , n , .
" " ( K=10 ) - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . classificação | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92.2 | 5 | 660 250 | 0 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82.8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 |
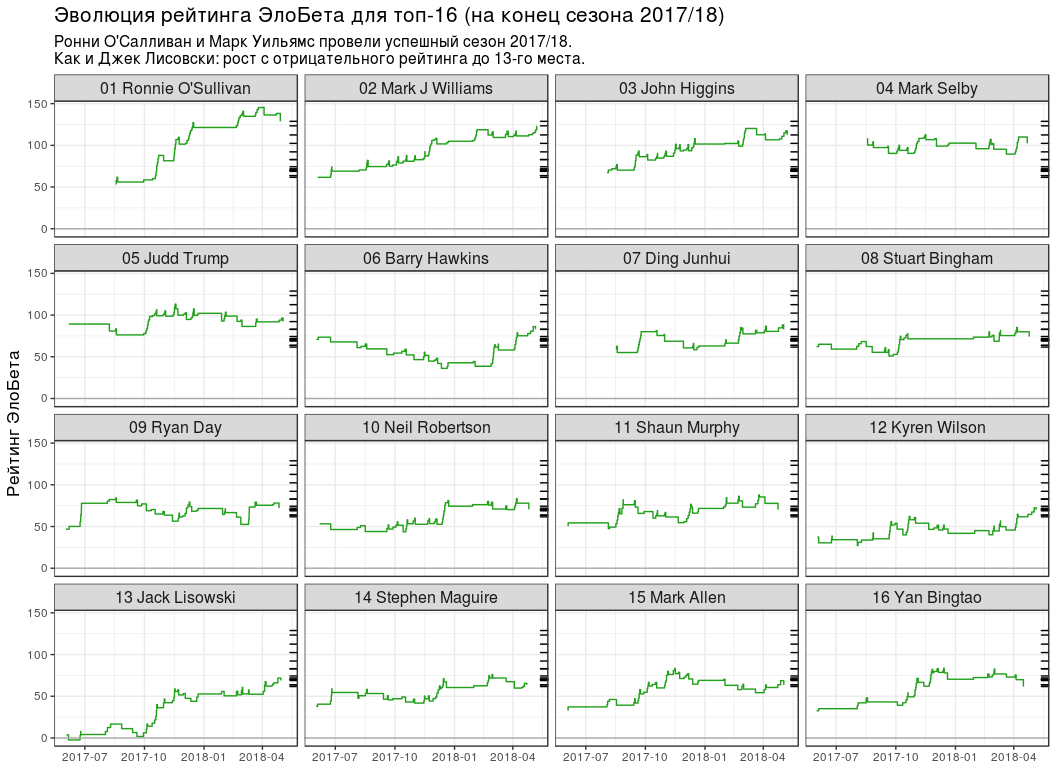
:
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
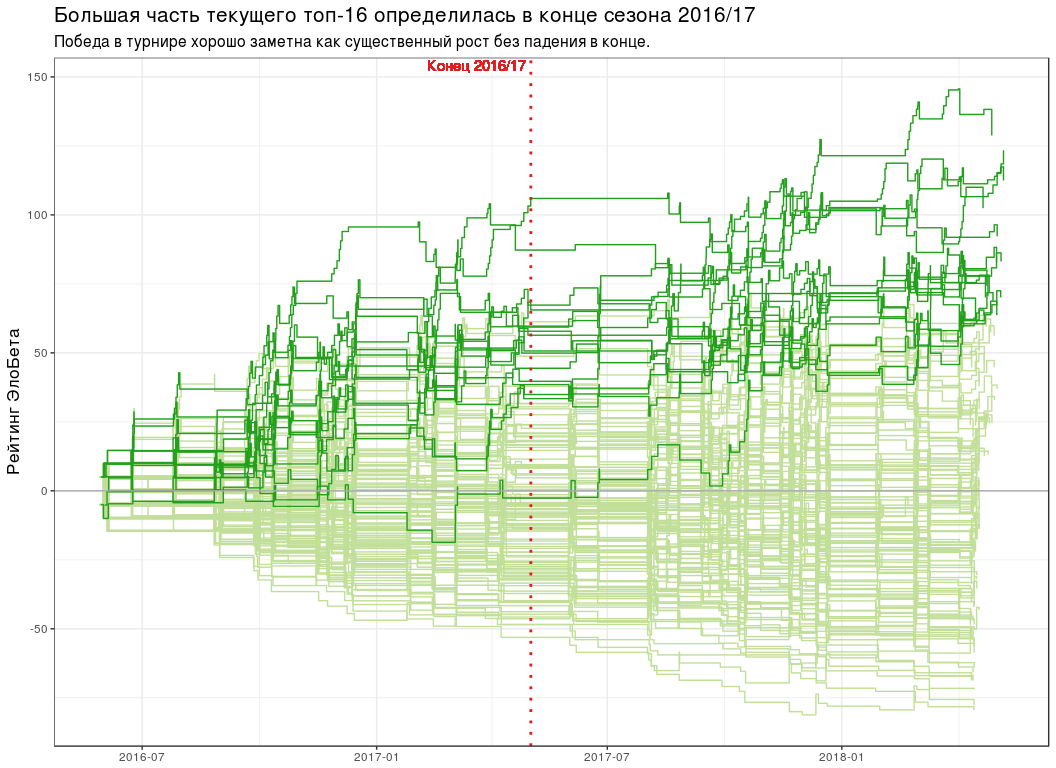
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
Conclusões
- " " R :
pbeta(p, n, m) . - — "best of N " ( n ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1