Continuo familiarizando os leitores de Habr com os capítulos de seu livro "Theory of Happiness", com o subtítulo "Fundamentos matemáticos das leis da maldade". Este livro científico ainda não foi publicado, informando de maneira muito informal sobre como a matemática permite que você olhe para a vida do mundo e das pessoas com um novo grau de conscientização. É para aqueles que estão interessados em ciência e para aqueles que estão interessados na vida. E como nossa vida é complexa e, em geral, imprevisível, a ênfase no livro está principalmente na teoria das probabilidades e nas estatísticas matemáticas. Aqui os teoremas não são provados e os fundamentos da ciência não são dados; isso não é de forma alguma um livro, mas o que é chamado de ciência recreativa. Mas é precisamente essa abordagem quase lúdica que nos permite desenvolver a intuição, animar as palestras para os alunos com exemplos vívidos e, finalmente, explicar aos não matemáticos e nossos filhos o que de tão interessante achamos em nossa ciência seca.
Falaremos sobre Fatum, terremotos, filas e processos maravilhosos: fluxo de Poisson, caminhada aleatória e um pouco sobre as cadeias de Markov.
Lei da zebra
Dizem que a vida é como uma zebra: uma listra branca ou preta ... E também acontece que outra é adicionada a um problema, e é tão difícil na vida, e então o gato começou a dar à luz! É grosso, está vazio! Um para um! Mas o mais triste é que, quando uma faixa brilhante entra bem e na vida, surgem maus pensamentos: oh, não seria uma bobagem, oh, não seria necessário pagar pela felicidade ... Uma sensação familiar? Nesta ocasião, uma das leis da merfologia é formulada - a segunda lei de Chisholm: "
Quando as coisas estão indo bem, algo deve acontecer em um futuro muito próximo ". Mas como Francis Chisholm, em seu
trabalho original, não fornece uma análise detalhada ou evidência dessa lei, tentaremos descobrir por nós mesmos se existe alguma regularidade por trás disso ou apenas nos parece. E se essas são as peculiaridades da matemática, é possível determinar a duração ou a frequência característica das listras no corpo de nossa zebra e de que depende?
Na vida, os eventos acontecem o tempo todo. Às vezes, eles não estão de modo algum conectados, outras vezes formam cadeias de relações de causa e efeito. Discussões sobre essas conexões, correntes e o caminho predeterminado da vida podem nos levar muito longe, e falaremos sobre elas mais tarde. Enquanto isso, vamos tentar, como sempre, obter a menor quantidade de dados de entrada para a análise de nossa lei. Considere uma sequência de eventos não relacionados entre si e veja o que você pode obter com isso.
Eventos que não estão relacionados de maneira alguma e ocorrem no tempo são descritos aleatoriamente usando o conhecido
fluxo de Poisson . Corresponde a muitos fenômenos aleatórios, desde terremotos até a aparência de clientes na loja. O fluxo de eventos de Poisson é caracterizado pela
intensidade ou
densidade do fluxo - um parâmetro que determina o número esperado de eventos por unidade de tempo. Por exemplo, ao medir o tempo em dias, o valor do parâmetro
haverá uma cadeia de eventos aleatórios, em média, ocorrendo uma vez por semana. Isso não significa que os eventos ocorrerão com uma
frequência de uma vez por semana. Uma sequência de eventos pode não ter nenhuma frequência alocada. É melhor imaginar um fluxo de Poisson com uma intensidade de uma vez por semana assim: 52 semanas em um ano, o que significa que cerca de 52 eventos devem ocorrer por ano (em média, ao longo de muitos anos). Se escolhermos 52 datas aleatoriamente distribuídas uniformemente em um ano, elas podem ser consideradas os momentos do surgimento de eventos de Poisson completamente independentes.
Um exemplo de construção de um fluxo de Poisson com uma intensidade de 1/7 (o tempo é medido em dias). Durante um intervalo de 365 dias, 52 eventos não relacionados entre si foram distribuídos aleatoriamente.Além disso, não há dúvida de periodicidade nesses eventos, quando eles desejam, então isso acontecerá. Mas mesmo nessa bagunça, as estatísticas podem nos mostrar certos padrões. Por exemplo, a distribuição da duração dos períodos entre os eventos mostrados na figura anterior não será uniforme.
A densidade da distribuição das durações de intervalos entre 52 eventos espalhados aleatoriamente ao longo do intervalo de 365 dias.A distribuição das durações das lacunas tende a ser
exponencial , é mostrada por uma linha sólida. Para esta distribuição, o máximo (modo) é zero e o valor médio é exatamente 7 dias. Além disso, o desvio padrão também será igual a 7 dias. A igualdade do desvio padrão e o valor médio é uma propriedade característica da distribuição exponencial. Como você pode ver, essas características não garantem que uma semana passará entre os eventos, em média - sim, mas com mais freqüência - menos, além disso, intervalos bastante longos podem ser observados. Por fim, a mediana mostra que metade de todos os intervalos terá uma duração não superior a 5 dias. Intensidade e frequência não são a mesma coisa, este é um ponto muito importante!
Para ser justo, suponha que eventos bons e ruins aconteçam igualmente prováveis, mas eventos brilhantes e significativos acontecem com muito menos frequência do que eventos pequenos e insignificantes. Que seja uma vida normal em que a coloração emocional dos eventos obedeça à distribuição normal (gaussiana). Aqui está a aparência de um ano de destino sintético, como uma série de vicissitudes aleatórias absolutamente independentes da vida:
Uma série de eventos de várias cores emocionais, formando um fluxo de Poisson com uma intensidade de 2/7 (2 eventos em 7 dias).Embora nenhuma banda seja observada, há algum ruído. Cada evento passa sem deixar rastro, sem deixar nada na memória ou no humor. Isso não acontece, vamos dar ao nosso herói modelo uma memória, para iniciantes, ideal. Cada evento pode ser enterrado para sempre em sua memória e em seu humor, respectivamente, melhorando ou piorando. Aqui está uma imagem que podemos obter observando o destino de nosso herói por dez anos.
Eventos que se fundem na memória formam a coloração emocional da "vida sintética".Bem, bem, já vemos algum tipo de alternância de humor, mas a imagem saiu não muito alegre. Nosso herói, após uma série de mudanças de humor, entrou em profunda depressão. Que pena. Vamos tentar mais alguns destinos. Todos eles experimentam uma série de faixas claras e escuras, mas por um longo tempo ficam atolados, quer no desejo sem esperança, quer na felicidade transcendente. Isso acontece, é claro, mas isso é claramente anormal.
Alguns exemplos de "destinos sintéticos" de pessoas com memórias perfeitas.Relaxe, cara!
Descrevemos o destino de nosso modelo como um processo notável, denominado
passeio aleatório unidimensional e possui várias propriedades incomuns, entre as quais há
auto-similaridade , ou seja, a ausência de qualquer escala de tempo característica. Além disso, tendo à sua disposição um tempo ilimitado, um passeio aleatório pode levá-lo ilimitadamente longe e, além disso, certamente o levará a qualquer distância predeterminada sobre o valor inicial! Assim, não importa quão bons sejam seus negócios, se estiverem sujeitos a divagações aleatórias, eles certamente deslizarão para zero e descerão, é apenas uma questão de tempo! Esta famosa e instrutiva lei da vida, recebeu o nome
maldição do jogador e sua essência pode ser expressa por uma simples máxima:
A melhor estratégia no jogo é possuir um cassino, caso contrário, você perderá.
Não vamos nos debruçar sobre esse resultado, que já é muito conhecido, mas ainda encontraremos essa propriedade de caminhada aleatória unidimensional.
A memória emocional perfeita parece não ser muito boa. Nossos heróis não esquecem nada e lembram-se cuidadosamente de tudo, até dos eventos mais antigos! Seu humor na velhice é afetado pela dor de um brinquedo quebrado na infância ou pela alegria de um beijo na juventude. Além disso, todos os beijos e brinquedos subsequentes são de igual importância para eles. É necessário salvar esses pobres companheiros. As emoções diminuem com o tempo, o sofrimento se torna monótono, a alegria também também. Esquecer, de várias maneiras, é como resfriar, difundir ou desacelerar um movimento em um fluido viscoso; portanto, é aconselhável simulá-lo dessa maneira. Os processos listados são chamados de
processos de relaxamento . Vamos dar aos nossos pobres companheiros a capacidade de relaxar!
O sistema relaxante retorna ao estado de equilíbrio e, quanto mais rápido, maior o desvio do equilíbrio. Essa propriedade pode ser modelada por progressão geométrica ou
lei exponencial . Introduzimos um novo parâmetro em nosso modelo - a taxa de esquecimento
. Pode ser expresso no tempo (nas leituras do nosso modelo), durante o qual o nível de emoção diminuirá bastante. Por exemplo, para
o traço emocional do evento diminuirá em uma ordem de magnitude em dois meses. E agora a vida se tornou um bom "listrado"!
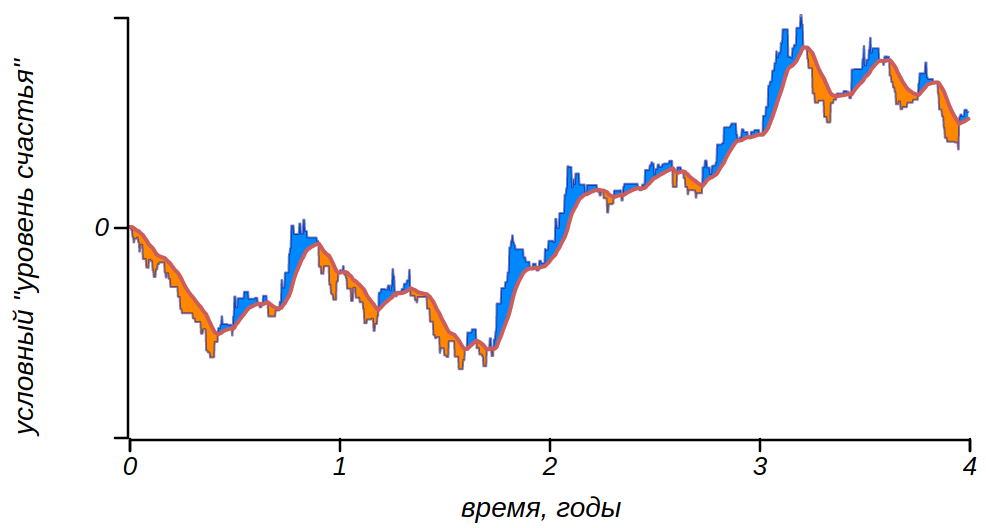
A limitação da memória leva ao fato de que uma série de eventos e seus traços na memória se fundem formam uma série de faixas emocionalmente coloridas.Mudando o "grau de esquecimento", podemos obter sujeitos experimentais mais ou menos emocionalmente equilibrados. Parece que encontramos uma fonte de zebra! Trata-se, em primeiro lugar, de passeios aleatórios, propensos a se espalhar em todas as direções e, em segundo lugar, curando o esquecimento, retornando o humor ao normal. O resultado é um clima sinuoso e ondulatório.
Vamos estudar as propriedades das faixas mundiais "sintéticas" que obtivemos. Construímos um histograma mostrando a distribuição de suas durações para uma vida longa (ou para muitas comuns) com parâmetros
.
A distribuição dos períodos de felicidade e sofrimento para um grande número de destinos sintéticos. A linha vertical marca o valor médio de 33.A primeira coisa que chama sua atenção - a distribuição máxima (moda) é próxima de zero, o que significa que na maioria das vezes os períodos de felicidade e infelicidade são muito curtos; no entanto, também existem períodos que duram mais de um ano. Em média, a duração dos períodos é de 33 dias, com um desvio padrão de 36 dias. Essa distribuição é próxima da exponencial (na verdade, é bem descrita por uma
distribuição gama mais geral com parâmetros que a aproximam da exponencial). Por sua vez, a distribuição exponencial dos comprimentos das bandas na vida significa que as mudanças de humor podem ser consideradas como um fluxo de Poisson, ou seja, como uma cadeia de eventos aleatórios independentes que não têm uma frequência alocada, mas acontecem com alguma intensidade conhecida. Por exemplo, no exemplo que examinamos, as faixas escuras e claras mudam com uma intensidade de uma vez a cada 33 dias, mas, ao mesmo tempo, períodos mais curtos são observados na vida: metade deles não dura mais que dez dias.
Na ausência de "memória" (por
), a distribuição deixa de diminuir exponencialmente e se torna exponencial.
A distribuição das durações dos meandros para uma caminhada aleatória tem a natureza de uma distribuição de energia.Os estatísticos dizem que essas distribuições têm uma
cauda pesada , o que torna muito grandes os desvios em relação ao valor médio, e os observamos na forma de “imersões” longas nesse outro humor. A distribuição obtida por nós possui uma propriedade incomum e estranha - nem o valor médio (valor médio), nem o desvio padrão, nem a mediana são definidos para ele. O fato é que todas essas características são calculadas com base na área sob a curva de densidade de distribuição e são infinitas. Nesse sentido, pode-se ouvir que o valor médio neste caso é infinito, mas não é assim. Veja o que acontece quando você tenta calcular o valor médio da duração do meandro de uma caminhada aleatória:
Tentando calcular o valor médio para uma sequência de períodos de períodos entre mudanças de humor na ausência de memória. Valores extremos emergentes da parte mais pesada da distribuição levam ao fato de que o valor da média não converge para nenhum valor.Grandes saltos originados da cauda pesada derrubam continuamente o valor médio e a sequência da média não converge para nenhum limite. O valor médio não é infinito, apenas a integral não converge para nenhum número e é impossível falar sobre qualquer valor específico. É a impossibilidade de calcular o valor médio da duração do meandro que reflete a propriedade de auto-similaridade dos passeios aleatórios, ou seja, a ausência de uma escala de tempo adequada.
Simulamos a adaptabilidade às turbulências cotidianas com a ajuda do relaxamento ou atenuação de explosões emocionais. Esse processo pode ser interpretado de outra maneira, como a adaptabilidade de uma pessoa às circunstâncias da vida. Ao processar sinais ou seqüências ruidosos, o método da média móvel é frequentemente usado para suavizar e selecionar um sinal útil, considerando a cada momento não o sinal em si, mas o valor médio do sinal durante um determinado período de tempo. Assim, é possível se livrar do ruído e ter uma idéia das tendências de longo prazo do sinal. Aplicando essa média à turbulência cotidiana, podemos simular a adaptabilidade humana. E durante as guerras, as pessoas se apaixonam e encontram motivos de alegria, assim como a vida de ricos ociosos não é sem nuvens. A norma está mudando, da qual o humor se desvia em uma direção ou outra. Considerando a diferença entre uma sequência de emoções e uma linha de fundo suave, obtemos a mesma imagem, listras, que o modelo anterior nos deu, com as mesmas características estatísticas. Isso não é surpreendente, porque conceitualmente eles praticamente não diferem, descrevendo um sistema com relaxamento.
Conectado por uma corrente
Nos modelos considerados, recebemos um fluxo de Poisson de mudanças de humor, gerando eventos com um fluxo de Poisson. Pode-se ver alguma manipulação nisso - o processo aleatório de Poisson acabou sendo “costurado” no modelo. Quão universal é o nosso resultado? É possível obtê-lo de alguma maneira diferente?
A experiência mundana é uma coisa mal formalizada e pode ser adaptada a várias ferramentas matemáticas, permitindo não apenas suposições simplificadoras, mas também especulação. Na ciência, essa abordagem é inaceitável, mas em nossa jornada pelos métodos da teoria dos processos aleatórios, podemos nos dar ao luxo de brincar com eles para conhecer melhor.
Observando a dinâmica do humor e da percepção do mundo, você pode ver que é da natureza humana “ficar” em um determinado humor. Se tudo estiver indo bem, as más notícias podem ser recebidas com otimismo. E, pelo contrário, o humor melancólico, uma vez engolido por uma pessoa, pode estragar até notícias alegres. Do ponto de vista matemático, isso significa que a probabilidade de permanecer no humor atual é maior do que a probabilidade de alterá-lo. Esse comportamento pode ser descrito usando um processo aleatório chamado de
cadeia de Markov . No caso geral, uma cadeia de Markov pode ser representada como um conjunto fixo de estados com transições entre elas, e as transições de estado para estado têm uma probabilidade diferente, mas conhecida. É conveniente representar essas cadeias na forma de gráficos ponderados; por exemplo, uma cadeia Markov simétrica elementar que descreve a dinâmica do humor pode ser representada desta maneira:
Cadeia de Markov com dois estados ("alegre" e "triste"). As setas indicam as transições e as probabilidades dessas transições. No nosso caso simétrico, a probabilidade de permanecer no estado de espírito existente excede a probabilidade de sua mudança, mas não depende do próprio estado de espírito.Nossa cadeia é capaz de gerar seqüências de estados e, é claro, bandas de zebras mundanas aparecerão nela.

O mais interessante é descobrir qual distribuição estará sujeita à duração dessas bandas. Para o nosso modelo mais do que simples, a resposta pode ser exata - essa é uma
distribuição geométrica que descreve a probabilidade de observar um determinado número de testes de um experimento aleatório antes de observar o primeiro "sucesso".
Um histograma para as durações de períodos do mesmo humor na sequência gerada pela cadeia simétrica de Markov e a função de probabilidade da distribuição geométrica com um parâmetro igual à probabilidade de transição entre estados. A sequência tem dez anos.Uma distribuição geométrica é um análogo discreto de uma distribuição exponencial, no sentido de que os valores arredondados de uma variável aleatória distribuída exponencialmente obedecem a ela. Existe uma relação entre o parâmetro de distribuição geométrica e a intensidade da distribuição exponencial correspondente.
Assim, obtemos novamente um fluxo de Poisson de mudanças de humor e, para a cadeia de Markov que descrevemos, sua intensidade é .
Se quebrarmos a simetria da cadeia, poderemos descrever um "otimista" ou "pessimista" que esteja mais disposto a "ficar" de um modo ou de outro. A distribuição das durações das tiras será diferente da geométrica, mas, ao mesmo tempo, a maioria das tiras será curta. e qualquer periodicidade destacada não será observada.Um histograma para as durações de períodos de humor constante na sequência gerada pela cadeia de Markov assimétrica. A sequência tem dez anos.As cadeias de Markov são uma ferramenta poderosa para analisar processos aleatórios nos quais reside um determinado algoritmo ou cenário. Eles nos dão uma visão peculiar dos processos que são considerados cíclicos. Por exemplo, a bem conhecida máxima: “a história da humanidade caminha em círculo” é frequentemente interpretada como o fato de que existem certos ciclos ou mesmo periodicidades na história. É preciso ouvir, por exemplo, que o início do século promete revoltas e guerras. Correndo o risco de entrar no meu próprio tópico, ousarei assumir que, de fato, faz sentido falar não sobre ciclos literais, mas sobre cenários mais ou menos estáveis - cadeias regulares que podem ser descritas por uma cadeia de Markov. Entre as cadeias de Markov, há uma classe de cadeias cíclicas que, de fato, são capazes de criar sequências repetidas.No entanto, não há uma periodicidade determinística verdadeira em seu comportamento. Ocorrendo aleatoriamente em diferentes períodos históricos e em diferentes contextos, esses ciclos são semelhantes entre si e podem criar uma sensação de “déjà vu” histórico. É útil estudá-los e descrevê-los, mas talvez você não deva esperar um plano estrito de calendário.Sobre isso, encerramos o tópico da zebra. Que conclusões podem ser tiradas de nossa pesquisa frívola? Uma série de faixas claras e escuras na vida não é uma ilusão, elas realmente são. Mas não há padrões particulares neles. Na maioria das vezes eles são curtos, mas também são prolongados. Tudo depende da facilidade de caráter e da capacidade de deixar ir o passado. Além disso, se os eventos da vida raramente acontecem, a vida se tornará uma série cinzenta de memórias desaparecendo no passado. Portanto, é do nosso interesse lembrar o que foi vivido e está ao nosso alcance garantir que a vida não se torne uma caminhada aleatória. Podemos fazer com que os bons eventos aumentem e aconteçam com mais frequência, mesmo que sejam insignificantes. Uma viagem de esqui, um sorriso sincero de quem passa, um ingresso para o show, uma xícara de chocolate quente em um dia frio,Tudo isso ajudará a criar uma tendência positiva e prolongar a linha brilhante da vida. É verdade que o valor médio seguirá a tendência, de modo que eventos tristes inevitáveis necessariamente mudarão o humor. Mas não culpe sua felicidade por isso. Isso não é uma retribuição para ele, e não o olho do mal. Essa propriedade de sistemas relaxantes é uma tendência a oscilações durante a ação externa estocástica.Sobre esperar um ônibus ou um terremoto
A diferença entre a frequência (período) e a intensidade do fluxo de eventos é importante o suficiente para entender ao ouvir notícias ou ler os resultados de pesquisas científicas. Por exemplo, hoje, os sismólogos, infelizmente, não podem prever um terremoto específico: tempo, lugar e força. Mas os métodos de previsão sísmica de longo prazo para algumas regiões foram desenvolvidos, mas seus resultados são formulados na linguagem da teoria das probabilidades, e o que fazer com elas nem sempre é óbvio.Por exemplo, para a Baía de Avachinsky, nas margens da qual Petropavlovsk-Kamchatsky está localizada em 2018, foi fornecida a seguinte previsão : “A probabilidade total de terremotos com magnitudes maiores que 7,7, que podem ter uma força de 7-9 pontos em Petropavlovsk-Kamchatsky, pode atingir 52,3 nos próximos cinco anos. %. " O que isso significa?
Tremendo amanhã? E quando? E onde Infelizmente, ainda não estamos em posição de responder a essas perguntas diretas. A interpretação exata dessa mensagem é a seguinte: a intensidade do fluxo sísmico é agora tal que, nos próximos 500 anos, ocorrerão aproximadamente 52 terremotos (assumindo que o fluxo permaneça inalterado). Além disso, em um mês a previsão pode mudar. A intensidade é semelhante, em certo sentido, à velocidade instantânea do movimento: para medir se você está se movendo a uma velocidade de 60 km / h, não é necessário dirigir uma hora inteira todos os 60 km. E, o mais importante, a previsão feita pelos cientistas não significa que decorrem dez anos entre os terremotos, como se pode supor, dividindo 500 anos em 52 eventos. Assim, se há dez anos não houver terremotos fortes, isso não significa que não acontecerá hoje ou amanhã. Isso acontecerá, é claro, mas quanto vai demorar para esperar,é desconhecido.Veja como o nível de atividade sísmica da região de Kamchatka muda em diferentes escalas de tempo (imagem retirada do site do Monitor de Atividade Sísmica da filial de Kamchatka do Levantamento Geofísico Unificado da Academia Russa de Ciências)O nível mais baixo de atividade é substituído por um aumento, a atividade "respira", mas não periodicamente, mas como o mesmo passeio aleatório com relaxamento.Mas os terremotos, no entanto, são fenômenos desagradáveis e não os deixam mais acontecer. Há coisas que você espera com muita impaciência, como um ônibus. Chegando ao ponto de ônibus, é claro que desejamos seguir instantaneamente a rota de ônibus ou bonde desejada, mas provavelmente isso falhará. Então, se houver um cronograma claro neste local, analisamos, depois o relógio e depois mergulhamos em um livro ou telefone. Porém, muitas vezes, no meio da rota, em vez da programação, o intervalo de tráfego é indicado, por exemplo, 15 minutos. Isso significa que já estamos longe da estação de ônibus com a qual os ônibus saem exatamente dentro do cronograma, e algum erro está se acumulando, tornando a chegada do ônibus aleatória. Bem, 15, então 15, vamos esperar. E aqui você deve ter em mente que, em média, você precisa esperar exatamente 15 minutos, independentemente de quando chegar.Agora, se os ônibus vieram decom uma frequência de 15 minutos, o tempo médio de espera seria metade do período - 7,5 minutos, mas com intensidade não funcionará! Na ausência de condições adicionais, o tráfego é modelado por um fluxo de Poisson, o que significa que o tempo de espera do ônibus obedecerá à lei exponencial com a mesma intensidade. E a expectativa matemática de uma quantidade distribuída exponencial com intensidade é igual a , . — , - . ,
, .
. , : , , : — . , 17 , , , , . , ,
efetivamente aumenta o tempo de espera observado.Curiosamente, a curva de Lorentz para a distribuição exponencial é a mesma para todas as intensidades. Assim, a afirmação é verdadeira para todos os processos de Poisson: metade do tempo total de observação ocorre em 20% dos casos quando este próximo evento é atrasado. O coeficiente de Gini para a distribuição exponencial é exatamente 1/2.Volta alienígena
Penso nas leis da maldade, na fila do aeroporto para o check-in de passageiros e bagagem. A fila é longa, as pessoas são diferentes e visíveis com todas as suas malas, crianças ou gaiolas. Ouço um grunhido por trás: “Como sempre, nossa vez é lenta. Olhe, olhe, aquele bigode em um boné estava em pé de igualdade conosco, e agora ali ... Essa é a lei da maldade! Minha vez é sempre lenta! Essa lei é chamada de observação de Ettore:"A próxima linha está sempre se movendo mais rápido."
Existe todo um campo da teoria do controle e da teoria dos processos aleatórios, que trata da dinâmica das filas. Isso é importante para o design de lojas e salas de espera, o gerenciamento ideal da sala de operações do banco, os portões da rodovia com pedágio e o gerenciamento de documentos. E o ponto de partida para modelar a fila é o mesmo fluxo de Poisson, pois requer um mínimo de suposições adicionais. Assim, os movimentos de quem está na fila assumirá a forma de uma linha escalonada em crescimento monótono, com os mesmos passos ocorrendo em intervalos aleatórios. A acumulação de dados dessa maneira é chamada de processo de Poisson .É assim que duas longas filas podem se mover:Movendo duas filas adjacentes enquanto Poisson processa com igual intensidade.Por sua vez, a diferença entre dois processos idênticos de Poisson, a saber, é observada por uma pessoa que está entediada na cauda, é uma espécie de caminhada aleatória. E se sim, então estamos prontos para tirar algumas conclusões. Primeiro: a distância entre as pessoas que estão simultaneamente nas mesmas filas aumentará ou diminuirá, e se formarão meandros característicos com uma duração em constante mudança. A segunda conclusão: devido à auto-similaridade de passeios aleatórios para rajadas curtas e longas, os meandros terão uma duração comparável ao tempo em que estão na fila, o que significa que serão perceptíveis e os meandros serão motivo de descontentamento. A terceira conclusão: não se sabe de antemão qual fila passará mais rápido, porque uma caminhada aleatória provavelmente passará para cima e para baixo. E, finalmente, a quarta conclusão: as filas se movem de forma independente, de vez em quando e se aproximam, em média, elas se movem da mesma maneira, e a diferença esperada entre elas tende a zero, mas a dispersão em torno da média aumenta com o tempo (no caso descrito por nós, o valor o atraso de uma fila em relação a outra está sujeito à
distribuição do Skellam ). Acontece, ou adivinhou com uma linha rápida ou não - não há coisas ruins do vilão do destino!
Mas as leis da maldade não seriam chamadas leis se não reivindicassem a universalidade. Se não tivermos sorte de estar na fila do atraso, passaremos mais tempo nela e teremos mais oportunidades de reclamar sobre o destino! E agora, atenção, boas notícias: em qualquer intervalo de tempo selecionado, aqueles que têm sorte de entrar na fila rápida mais do que pessoas infelizes, porque a fila rápida pode perder mais pessoas! Mas, infelizmente, isso não consolará quem está preso na fila.
O texto enviado ainda não foi publicado, o que significa que pode ser alterado. Espero que os comentários e observações dos leitores de Habr o ajudem a mudar para melhor.