Justificativa matemática pitagórica da escala musical

Um capítulo do livro de Alexander Voloshinov "Matemática e Arte" (Moscou: Iluminismo, 1992)

O venerável Pitágoras rejeitou a avaliação da música com base na evidência de sentimentos. Ele argumentou que as virtudes dela deveriam ser percebidas pela mente e, portanto, julgou a música não de ouvido, mas com base na harmonia matemática e achou suficiente limitar o estudo da música a uma oitava.

Plutarco

A rigor, estamos falando do sistema pitagórico. O que é gama e escala na música?

Gamma , ou escala , é uma sequência de sons (etapas) de algum sistema musical (traste), localizado a partir do som principal (tom principal), em ordem crescente ou decrescente. O nome "gama" vem da letra grega Gγ (gama), que na Idade Média denotava o tom extremo mais baixo da escala e depois a escala inteira.

A característica mais importante de um som musical é seu tom , que é um reflexo na consciência da frequência de oscilação de um corpo sonoro, como uma corda. Quanto maior a frequência de oscilação da corda, mais alto o som aparece para nós.

Cada som individual não forma um sistema musical e, se não for muito alto, não nos causa muita reação. No entanto, já a combinação de dois sons em outros casos acaba sendo agradável e harmoniosa e, em outros, pelo contrário, "corta" a orelha. Uma combinação acordada de dois sons é chamada consonância , uma combinação inconsistente é chamada dissonância . É claro que a consonância ou dissonância de dois tons é determinada pela distância da altitude entre esses tons ou o intervalo.

O intervalo entre dois tons é o número de série do tom do tom superior em relação ao mais baixo nesta escala, e o coeficiente de intervalo I _{21 de} dois tons é a razão entre a frequência do tom superior e a frequência do tom mais baixo ^* :

(6.1)

^* ( Na teoria da música, os conceitos de intervalo e coeficiente de intervalo não são estritamente distinguidos. Seguindo a tradição, geralmente nos referimos ao coeficiente de intervalo para brevidade como um intervalo. )

Vamos agora considerar um certo conjunto de sons pressionando, por exemplo, várias teclas no piano. Provavelmente, teremos um conjunto de sons incoerentes, como se costuma dizer, nem o armazém nem a preocupação. Em outros casos, os sons parecem se encaixar, se dão bem, mas a combinação deles parece irregular, inacabada. Eu gostaria de continuar esta sequência com uma certa nota, que neste sistema de sons parece ser a mais estável, básica e denominada tônica . Assim, os sons em um sistema musical são interconectados por certas dependências, algumas são instáveis e gravitam para outras - estáveis .

Mas não apenas o tônico e a combinação de sons estáveis ​​e instáveis ​​determinam a natureza do sistema musical. É fácil garantir que, pressionando oito teclas brancas seguidas da nota para (escala maior natural ) e da nota a ( menor natural ), essas escalas soem diferentes: a primeira - maior - soa alegre e leve, e a segunda - menor - triste e nublado ^* . Portanto, há outra característica do sistema de som - o humor: maior ou menor. Assim, chegamos a um dos conceitos mais complexos da teoria da música - o conceito de traste.

^* (A natureza do som do traste, é claro, não é definida de maneira tão grosseira e inequívoca. Essa questão é muito delicada, e falaremos sobre isso no final do capítulo. )

Um traste é uma interação de sons musicais agradáveis ​​à audição, determinados pela dependência de sons instáveis ​​em relação aos estáveis, e antes de tudo no principal tônico-som estável e com um certo caráter sonoro. A história da cultura musical conhece muitos modos característicos de diferentes povos e tempos diferentes. Os gregos antigos conheciam cerca de uma dúzia de trastes, e os trastes de alguns países do leste e da Índia são extremamente complexos, peculiares e incomuns para a audição européia. Os modos modernos mais comuns consistem em sete etapas principais, cada uma das quais pode aumentar ou diminuir, o que fornece mais cinco sons. Assim, o traste gama diatônico (7 etapas) se transforma em cromático (12 sons). O primeiro passo do traste é o tônico. As leis da estrutura do traste são uma ciência inteira, a pedra angular da musicologia, e muitos cientistas e compositores dedicaram a vida inteira ao estudo dessas leis.

Estaremos interessados ​​principalmente nas leis matemáticas que descrevem a estrutura do traste, isto é, o sistema musical. O sistema musical é a expressão matemática de um certo sistema de relações de afinação. Além do interesse puramente teórico, o sistema encontra aplicação na afinação de instrumentos musicais com um tom fixo de sons, como um piano ou órgão.

Concluindo, observamos que nossos experimentos com o pressionamento das teclas do piano podem terminar com o fenômeno mais raro e agradável, quando o sistema de som utilizado não apenas pertence a um fret, mas também tem significado. Uma série seqüencial artisticamente significativa de sons de diferentes alturas é chamada de melodia . É exatamente isso que gostamos de cantarolar, dependendo do nosso humor - alegre, triste, alegre ...

Após uma excursão tão curta à musicologia teórica, podemos voltar às margens do ensolarado Hellas durante o tempo dos sábios Pitágoras. Tentaremos restaurar o raciocínio de Pitágoras e seus alunos ao construir o sistema pitagórico, porque foi esse sistema que determinou por milênios, se não para sempre, todo o desenvolvimento da cultura musical, não apenas européia, mas também oriental. O próprio Pitágoras não deixou nenhuma obra escrita, e o legado dos pitagóricos parece ser uma pilha sem esperança de ruínas, isto é, uma coleção de fragmentos sobreviventes acidentalmente e citações posteriores. Sem dúvida, essas ruínas são lindas e ainda surpreendem a imaginação, como as ruínas do famoso Partenon, mas muitos desses fragmentos estão completamente perdidos e você geralmente pode adivinhar o todo. E ainda ...

O monocórdio - corda única - foi um dos primeiros instrumentos musicais dos antigos gregos. Era uma caixa comprida necessária para amplificar o som sobre o qual a corda foi puxada. De baixo, a corda foi puxada por um suporte móvel para dividi-la em duas partes que soavam separadamente. Em uma caixa de madeira sob a corda, havia uma escala de divisões, o que tornava possível determinar com precisão qual parte da corda soa. É claro que, como instrumento musical, o monocórdio nos parecerá muito primitivo, mas era um excelente instrumento físico e uma ferramenta de ensino na qual os antigos contempladores compreendiam a sabedoria da alfabetização musical.

Os antigos afirmavam que Pitágoras já conhecia as leis da vibração de uma corda de monocórdio e a construção de consoantes musicais (consonâncias); no entanto, encontramos um registro dessas leis do arquito pitagórico de Tarento (428-365 aC), que viveu um século e meio depois de Pitágoras . O arquiteto era, é claro, o representante mais proeminente da escola pitagórica, um amigo do filósofo Platão e professor do matemático Eudoxus (c. 408 - c. 355 aC), estadista e comandante. A versatilidade de Architus é incrível: ele resolveu o famoso problema de dobrar o cubo, foi merecidamente considerado o maior teórico da música pitagórica, o primeiro a otimizar a mecânica baseada na matemática e reduzir os movimentos dos mecanismos aos desenhos geométricos, trabalhar em um modelo de madeira de uma pomba voadora. Segundo Van der Waerden, Arch é o autor do VIII livro "The Beginnings" of Euclid, que estabelece a teoria aritmética das proporções. Como estadista, Archit era extremamente respeitado: ele foi eleito estrategista sete anos seguidos ^* , embora por lei os estrategistas tenham sido escolhidos apenas por um ano. Através de manobras diplomáticas hábeis, o Arquit resgatou Platão do cativeiro e, assim, salvou a vida do grande filósofo. "Arquitetos gloriosos, terras e mares e calculadora de areia ..." - escreveu Horace.

* ( Estrategista - nas antigas cidades-estados gregas, um líder militar dotado de poderes políticos e militares Shi-ki. )

As "Leis de Pitágoras-Arquita", nas quais toda a teoria da música pitagórica se baseava, podem ser formuladas da seguinte maneira:

1- O passo (frequência de oscilação f) da corda sonora é inversamente proporcional ao seu comprimento l:

(6.2)

aqui a é o coeficiente de proporcionalidade, dependendo das propriedades físicas da corda (espessura, material, etc.).

2. Duas cordas sonoras dão consonância somente quando seus comprimentos são referidos como números inteiros que compõem o número triangular 10 = 1 + 2 + 3 + 4, ou seja, 1: 2, 2: 3, 3: 4.

Esses intervalos são "consonâncias perfeitas", e seus coeficientes de intervalo receberam os nomes latinos ^* :

^* ( Os nomes dos intervalos na música são números latinos, que indicam o número de série da escala da escala que compõe o intervalo com o estágio inicial: oitava - oitava, quinta - quinta, quarta - quarta, etc. )

oitava

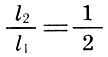
quint

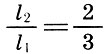
quart

Número triangular 10

Também foi observado que a fusão mais completa de tons é dada por uma oitava (2/1), seguida por um quint (3/2) e um quart (4/3), ou seja, quanto menor o número n em relação à forma 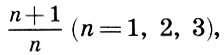quanto mais consoante o intervalo.

"A segunda lei de Pitágoras - Arquita" e agora parece surpreendente. O que podemos dizer sobre os pitagóricos, a quem ele simplesmente encantou! Aqui eles encontraram a confirmação de toda a sua filosofia: números inteiros, além disso, os números tetraktis governam tudo, até a música! Os pitagóricos não se demoraram e estenderam a lei das relações musicais sempre que possível, incluindo a estrutura do universo.

Portanto, se considerarmos o segmento l igual a 1/12 do comprimento da corda monocromática l ₁ como o preço da divisão da escala de monocordas, juntamente com toda a corda monocromática de comprimento l ₁ = 12l suas partes do comprimento l ₂ = 6l serão consoantes - o som é uma oitava maior (l ₂ / l ₁ = l / 2), l ₃ = 9l - soe um quinto mais alto (l ₃ / l ₁ = 2/3) e l ₄ = 8l - soe um quarto mais alto (l ₄ / l ₁ = 3/4 ) Essa consoante e seus números de definição 6, 8, 9, 12 foram chamados tetrad (quatro). Os pitagóricos acreditavam que o tetrad era "aquela escala segundo a qual as sirenes cantam". Ao afinar a lira antiga, que se tornou o símbolo da música, suas quatro cordas eram necessariamente afinadas de acordo com a regra do tetrad, e a afinação das cordas restantes dependia do traste para tocá-la.

Mas para o pensador antigo não bastava estabelecer os valores numéricos das quantidades estudadas. O olho e a mente pitagóricos estão acostumados não apenas a medir, mas também a medir, ou seja, a revelar as conexões internas entre os sujeitos estudados, ou seja, a estabelecer relações proporcionais. O arquiteto era um verdadeiro pitagórico e estabeleceu relações proporcionais entre a principal consonância perfeita - uma oitava, uma quinta e uma quarta. Esta decisão foi obtida pelos arquitetos em conexão com o desejo de dividir a oitava em intervalos harmoniosos. Provavelmente, o Arch baseia-se na suposição intuitivamente óbvia de que, junto com os tons f ₁ ef ₂ = 2f ₁ , dando a consoante principal - uma oitava, a consonância e sua média aritmética f ₃ = (f ₁ + f ₂ ) / 2 devem fornecer. Porém, o comprimento da corda l ₃ será expresso em termos dos comprimentos da corda l ₁ e l _{2 de} acordo com (6.2) da seguinte maneira:

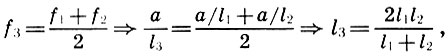
isto é, l3 é a média harmônica l1 e l2 (ver 5.1). O oposto também é fácil de detectar: ​​a média harmônica das frequências f ₁ ef ₂ vai para a média aritmética dos comprimentos l ₁ e l ₂ :

Lembrando que 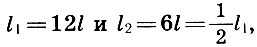Juntamente com os arquitetos, chegamos a uma conclusão importante:

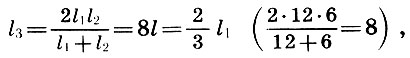
(6.3)


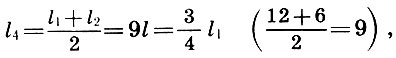
(6.4)

ou seja, o quinto é a média harmônica dos comprimentos das cordas do tom fundamental l ₁ e oitavas l ₂ , e o quart é a média aritmética de l ₁ e l ₂ .

Mas o produto da média aritmética e da média harmônica é igual ao produto dos números originais:

(6,5)

daí, dividindo ambas as partes por l ₁ ² , obtemos a segunda conclusão importante:

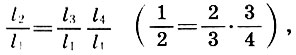
(6,6)

ou

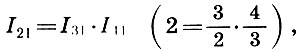
isto é, uma oitava é o produto de um quinto a um quarto.

Dividindo (6,5) por l ₁ l ₃ , o Archite obtém a terceira das principais proporções - geométrica:

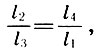
(6,7)

que foi chamado de "musical": uma oitava se refere a um quintal, tanto quanto um quarto, a um tom fundamental .

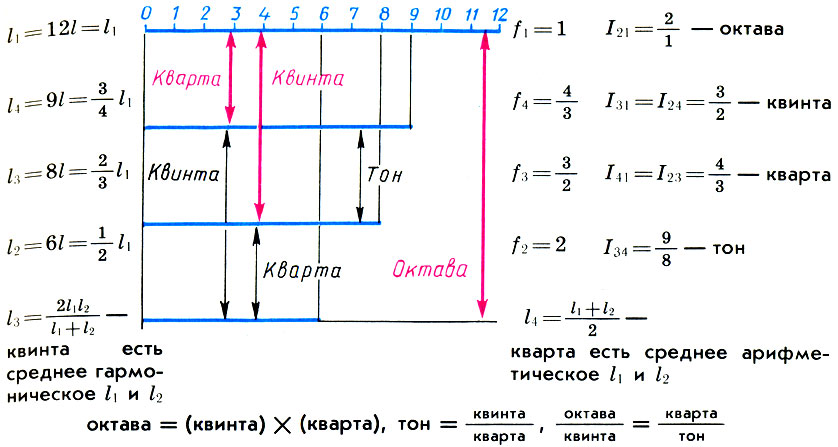
Divisão de uma corda de monocorda (l ₁ ) em partes que formam consonâncias perfeitas com ela: uma oitava (l ₂ ), uma quinta (l ₃ ) e um quarto (l ₄ ) e as relações entre elas. Os intervalos que uma cadeia inteira de monocordes forma com suas partes são mostrados por setas vermelhas

É fácil obter mais duas relações:

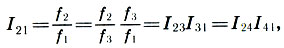
(6,8)

isto é, a oitava é dividida em dois intervalos consoantes desiguais - o quinto e o quarto . Um intervalo que estende esse intervalo a uma oitava é chamado de inversão . Assim, o quint é o inverso do quart e vice-versa.

Finalmente, encontramos o coeficiente de intervalo entre as cordas da quinto l ₃ e do quart l ₄ , que juntamente com seu intervalo é chamado tom (não confunda o intervalo e o som de uma determinada altura):

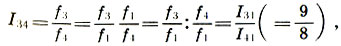
(6,9)

ou seja, o intervalo de tons é igual à proporção do quinto ao quarto .

Observe que, ao contrário da distância usual na linha reta r ₂₁ = x ₂ - x ₁ definida como a diferença entre as coordenadas do final e do início, o coeficiente de intervalo - a distância da altitude - é definido como a razão de seus tons constituintes 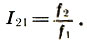Então, três tons f ₁ <f ₂ <f ₃ localizados em distâncias iguais r e formando uma progressão aritmética x ₁ , x ₂ = x ₁ + r, x ₃ = x ₁ + 2r. Portanto, os coeficientes de intervalo são adicionados e subtraídos “geometricamente”, e os próprios intervalos - “aritmeticamente”, como distâncias usuais, a saber:

a soma de dois intervalos é igual ao produto dos seus coeficientes de intervalo:

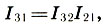
(6,10)

a diferença de dois intervalos é igual ao quociente de seus coeficientes de intervalo:

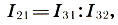
(6,11)

dividir o intervalo em n partes iguais significa extrair uma raiz do grau n do seu coeficiente de intervalo:

(6,12)

etc.

Para passar dos coeficientes de intervalo para os intervalos de distância, basta introduzir o intervalo logarítmico L = log _a I e a frequência logarítmica F = log _a f. Então, logaritmo de definição (6.1) e igualdades (6.10) - (6.12), obtemos a definição e as regras de ação usuais com distâncias:

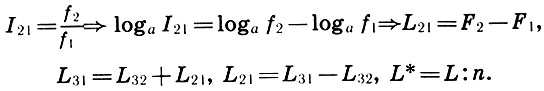
(6,13)

A solução do problema da divisão de oitavas levou a Archit imediatamente duas evidências de irracionalidade . De fato, se tentarmos dividir a oitava em dois intervalos iguais I, então, colocando (6.8) I ₂₃ = I ₃₁ = I, temos

Mas com essa proporção de comprimentos de cordas, uma clara dissonância é ouvida. Como a consonância é determinada pela razão de números inteiros da forma (n + 1): 2, a ideia sugere que o número não pode ser expresso pela razão de dois números inteiros, isto é, é irracional.

A segunda prova de irracionalidade menos musical, mas mais matemático. Para encontrar a raiz quadrada de um número que não é um quadrado completo, o Archit o decompõe em dois fatores desiguais (2 = 1 * 2), forma a média aritmética 3/2 e a média harmônica 4/3 desses fatores e compõe uma proporção musical a partir desses números ( 6.7):

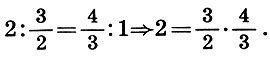
O produto dos termos médios dessa proporção é igual a um determinado número 2 e sua diferença menor que a diferença da aproximação zero 2 - 1 = 1. Portanto, pode ser considerado como valores aproximados .

(3/2 com excesso, 4/3 com deficiência).

Tendo realizado o mesmo procedimento nas primeiras aproximações, obtemos as segundas aproximações:

além disso

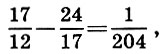
e depois as terceiras aproximações:

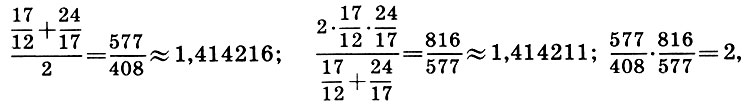
além disso

1.414216-1.414211 = 0.000005.

Como esse procedimento pode ser repetido indefinidamente, fica claro que o número irracional. Ao longo do caminho, estamos convencidos da validade da ideia pitagórica de que quanto maiores os números inteiros na relação, mais precisamente eles expressam o número irracional (ver p. 96). Finalmente, lembrando-se desse significado é igual a 1,414213 ..., vemos que o método "musical" do Archit converge muito rapidamente para o valor exato e já a terceira aproximação fornece cinco casas decimais corretas!

Mas voltando aos nossos intervalos. Assim, a oitava é dividida em duas consoantes desiguais do quinto e quarto, e o quinto - pelo quarto e pela dissonância. O intervalo de tom foi tomado como o intervalo entre os sons vizinhos (passos) de altura ao construir a escala de Pitágoras. Aqui está a chave para construir uma preocupação. Segundo o musicólogo soviético L. A. Mazel, o intervalo do quinto, dividido em quart e tom, é o principal elemento musical. 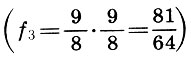Ao escolher o tom como o principal modo de formação, os teóricos antigos apenas precisam deixar de lado o som principal então outro tom e o intervalo restante entre o segundo tom e o quart tone 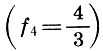chamar meio-tom 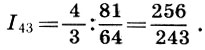Esse nome é bastante justificado, pois dividir o intervalo de tom pela metade de acordo com a fórmula (6.12) fornece 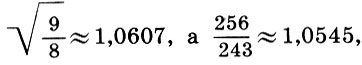ou seja, um semitom é quase igual a meio tom ^* . Assim foi obtida a base de toda a música grega antiga - tetracord - uma escala de quatro cordas dentro de um quarto.

^* (O intervalo de tom (semitom) na teoria musical é aceito como a unidade de medida aritmética dos intervalos, e os intervalos de tom e semitom, em contraste com seus coeficientes de intervalo, são chamados grandes e pequenos segundos. )

É claro que existem apenas três possibilidades para a posição do semitom no tetracord, que determinou a natureza e o nome do tetracord:

Dorian: meio -tom - tom - tom;

Frígio: tom - semitom - tom;

Lídio: tom - tom - semitom .

Os nomes dos tetrachords indicam as respectivas regiões da Grécia e da Ásia Menor, cada uma das quais cantou em sua própria harmonia.

É claro que quatro cordas dentro de um quarto não eram suficientes para conduzir a melodia, então os cordões do tetraconexão. Já descobrimos que uma oitava consiste em dois quartos e um tom; , , . , , «». «» — . :

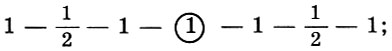
1 , 1/2 — , . . , , , (2 — , 3 — , - - - - - - c - o ), — ^* .

^* ( «» , (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) , — . )

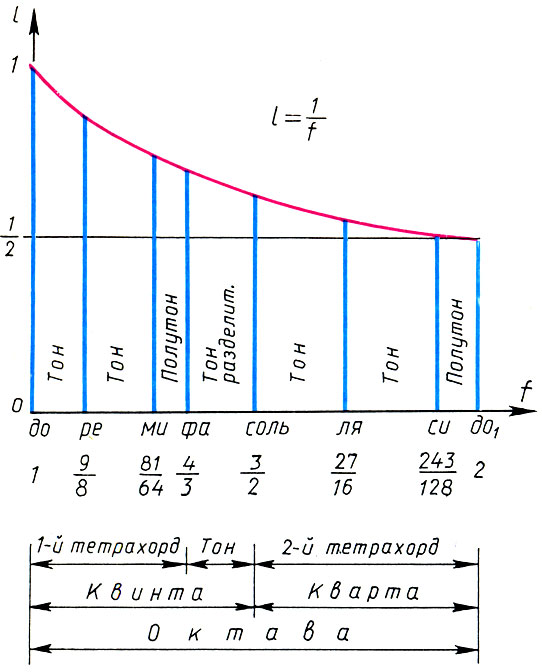Sistema de Pitágoras da gama lídia e suas características matemáticas

, , , , , . . . f ₁ = 1, o : f ₁ = 1, f ₂ = ⁹ / ₈ , f ₃ = ⁹ / ₈ * ⁹ / ₈ = ⁸¹ / ₆₄ , f ₄ = ⁴ / ₃ . : f ₅ = ³ / ₂f _l = ³ / ₂ , F ₆ = ³ / ₂ f ₂ = ^{27 de} / ₁₆ , F ₇ = ³ / ₂ f ₃ = ₂₄₃ / ₁₂₈ , f ₈ = ³ / ₂ f ₄ = 2. Por fim, temos por coeficientes de intervalo

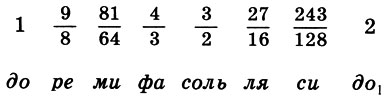(6.14)

Este é o cânon de Pitágoras. Segundo a lenda, o cânon de Pitágoras encontrou aplicação prática pela primeira vez na afinação da lira do lendário Orfeu.

. «» , . . , -(-), — - (-). 6 , (- — — ) . , . , , . , , . 1 , , , , — , . .

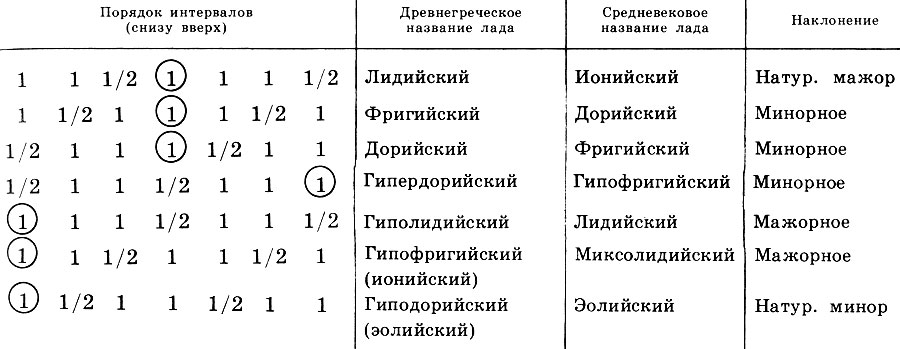Tabela 1. A sequência dos intervalos de tom (1) e semitom (1/2) em trastes antigos (de baixo para cima), nomes gregos e medievais antigos de trastes e sua inclinação

Se lembrarmos que agora apenas dois trastes dominam - maior e menor, podemos apenas imaginar o quão sofisticada era a antiga consciência musical. Os gregos enchiam cada lado de um certo conteúdo ético e estético, seu “ethos”, estabelecendo uma conexão clara entre imagens musicais e estados da alma. Funções mágicas e até médicas foram atribuídas à música, mas uma importância especial foi atribuída à música como meio de educação.

Dança menada. Alívio

, «» , . , , ,- (. 551-479 . . .), : « , — ». , , , . , , , , . , , , . , . , , . , , «» , , , , .

Aristóteles na política julga as preocupações, talvez ainda mais rigorosas que Platão, reconhecendo apenas o modo dórico como um modo capaz de treinar a psique. No entanto, Aristóteles faz uma classificação "ética" detalhada dos modos, distinguindo modos que causam equilíbrio mental (Doriano), pelo contrário, violam-no (modo hipofrigiano - "mesa"), excitam a vontade e o desejo de ação (modo hipodoriano da tragédia grega), causar um estado de êxtase e êxtase (frígio, hipólido).

Encontramos uma bela descrição do "ethos" dos trastes gregos no livro do escritor romano antigo Apuleius (c. 124 -?) "Florids": "Costumava haver um flautista chamado Antigenides. Todo som no jogo desse músico era doce, todos os trastes eram familiares para ele, e ele podia recriar para você, de acordo com sua escolha, a simplicidade do traste Eólio, a riqueza dos Jônicos, a tristeza dos Lidianos, a alegria dos Lígios, a alegria dos Frígios e a militância de Doria. ”

No entanto, pare! Existe uma contradição aqui? O humor dórico é chamado beligerante, mas na verdade é, de fato, nosso menor! Como o humor dórico era considerado verdadeiramente grego, verifica-se que o personagem principal da música grega é triste, menor. Para os gregos, o humor dórico é uma expressão de vivacidade, alegria e até militância. É assim que o destacado estudioso contemporâneo da antiguidade, o último filósofo da “era da prata” russa, Professor A. F. Losev (1893-1988) ^* explica: “A arte grega é uma afirmação de vida invariável”. Restrições nobres e até tristeza não deixam o grego, mesmo quando ele está se divertindo, quando está alegremente construindo sua vida, quando está em guerra e morrendo. Os trastes "alegres", de uma maneira ou de outra, gravitam em direção a esse luto bonito, nobre, vigoroso, importante e ao mesmo tempo majestosamente triste - Dorian. O clima dórico é o estilo escultórico da música grega ... Portanto, toda a escultura grega é muito atenciosa, triste e nobre. ”

^* ( O destino de Aleksei Fedorovich Losev é feliz e trágico. Ele está feliz porque, até o último dia de sua vida de 95 anos, Losev manteve uma incrível capacidade de trabalho e conseguiu concluir o trabalho principal - os oito volumes “História da estética antiga”. Trágico, porque os outros oito volumes de suas obras são escritos. meio século antes (1927 - 1930), eles foram anatematizados, e o próprio autor, sendo reprimido ilegalmente, continuou sua pesquisa filosófica sobre a construção do Canal do Mar Báltico-Branco, de onde escreveu: “Estou acorrentado quando minha alma está fervendo forças eternas e inesgotáveis. "Uma dessas obras de Losev," A música como tema da lógica ", poderia servir como uma luz norteadora para este livro. No entanto, o destino de A.F. Losev é feliz, porque os manuscritos não queimam. Hoje, a grande herança filosófica de A F. Losev recupera seu renascimento. )

Mas e o caminho da Lídia? Afinal, este é exatamente o nosso curso principal, enquanto Apuleio chama isso de triste, e Platão - funeral! Bem, ao avaliar o traste lídio, Aristóteles não concordou com Platão, encontrando infantilidade e charme ingênuos no traste lídio e atribuindo-o a trasgos que causam equilíbrio mental. Com o tempo, o modo lídio perdeu seu caráter deplorável, e os teóricos da antiguidade começaram a falar mais frequentemente sobre a "doce melodia lídia" ou a "diversa melodia lídia".

Assim, vemos que a questão do "ethos" dos trastes não é resolvida sem ambiguidade e é amplamente determinada pela tradição de aplicar esse ou aquele traste. E em nosso tempo, o ouvinte, criado, por exemplo, em uma música indiana sutil e peculiar, não distingue entre maior e menor, sem mencionar seu “ethos”. É claro que o clima principal é distinguido por tons mais claros e alegres, e há razões objetivas para isso, que discutiremos no capítulo 10. Mas a realização dessas possibilidades depende de uma série de outros fatores (ritmo, ritmo, padrão melódico etc.) e, portanto, existem muitos trabalhos alegres e enérgicos em pequenas e tristes, meditando em grandes. Lembremos pelo menos a "Sonata Patética", no menor Beethoven, esse monólogo apaixonado e ardente do Herói, pedindo uma batalha feroz e até a morte. Muitos artistas escolheram muitos epítetos para esta sonata (embora, talvez, o melhor deles - patético - pertença ao próprio Beethoven), mas não pode ser chamado apenas de triste - menor. Pelo contrário, Nocturne No. 2 Op. O nono maior major de Chopin é permeado por um clima de devaneio suave. Essas são lembranças tristes e nebulosas do autor, mas de modo algum uma peça alegre e importante. Em conclusão, vamos tentar dizer algumas palavras sobre o "ethos dos intervalos", porque o presente capítulo é dedicado à análise de intervalos musicais. Vamos tentar, porque essa questão é ainda mais controversa e pouco desenvolvida do que o "ethos dos trastes". E ainda ...

Até o momento, não dissemos nada sobre a “consonância mais perfeita” - prima (uníssono) (l ₂ / l ₁ = 1, ou seja, duas cordas produzem um som da mesma altura), porque, do ponto de vista da matemática, esse intervalo não é de interesse. No entanto, na orquestra, esse intervalo mais simples desempenha um papel enorme, fornecendo esse volume e brilho ao som.

A próxima consonância perfeita é a oitava. Ao mesmo tempo, a oitava também dá a impressão de um som tridimensional e, com um som seqüencial, uma sensação de espaço e amplitude. Uma excelente ilustração disso é a "Canção da pátria", do compositor I. O. Dunaevsky (1900-1955). Em seu coro ("De Moscou até os arredores ..."), uma oitava ascendente (l ₁ / l ₂ = 2) soa duas vezes, pintando as vastas extensões de nossa Pátria. Aqui, depois de duas oitavas, existe um quinto ascendente. Uma quinta (l ₁ / l ₂ = 3/2) também soa larga, mas mais texturizada e dinâmica do que uma oitava.

As melodias de muitas canções e hinos revolucionários começam com um intervalo de um quartzo ascendente (l ₁ / l ₂ = 4/3), por exemplo, Internacional, Hino da União Soviética, Marselha. Aqui, o intervalo de um quarto soa resolutamente e ativamente, como uma chamada à ação.

Há um "ethos" especial no intervalo de um segundo: com som simultâneo, é dissonante e desagradável, mas com som sucessivo o anterior transborda para o próximo, formando o fluxo natural da melodia de um som para outro. Em uma melodia, os intervalos entre dois sons de referência são frequentemente preenchidos em segundos intervalos consecutivos. Por exemplo, a música “Um vidoeiro apareceu no campo” começa com um quinto intervalo cheio de segundos consecutivos, o que dá a impressão de um fluxo calmo e imponente da melodia, como imagens imponentes e calmas da natureza russa.

E o mais desagradável e dissonante é o intervalo triton ou semi-oitava (l ₁ / l ₂ = ) Por sua inconsistência, esse intervalo "levou" o arquita a "prova musical" de irracionalidade .

Agradecemos à Biblioteca de Matemática por digitalizar o livro.