Richard Hamming: Capítulo 10. Teoria da Codificação - I

"O objetivo deste curso é prepará-lo para o seu futuro técnico."

Oi Habr. Lembre-se do incrível artigo “Você e seu trabalho” (+219, 2442 favoritos, 394k leituras)?

Portanto, Hamming (sim, sim, códigos de Hamming com auto-verificação e auto-correção) tem um livro inteiro escrito com base em suas palestras. Estamos traduzindo, porque o homem está falando de negócios.

Este livro não é apenas sobre TI, é um livro sobre o estilo de pensamento de pessoas incrivelmente legais. “Isso não é apenas uma carga de pensamento positivo; descreve condições que aumentam as chances de fazer um ótimo trabalho. ”

Já traduzimos 28 (de 30) capítulos. E estamos trabalhando em uma edição em papel.

Teoria da codificação - I

Tendo considerado os computadores e o princípio de seu trabalho, consideraremos agora a questão da informação: como os computadores representam a informação que queremos processar. O significado de qualquer caractere pode depender de como ele é processado, a máquina não possui significado específico para o bit usado. Ao discutir a história do software, capítulo 4, consideramos uma linguagem de programação sintética, na qual o código da instrução break coincidiu com o código de outras instruções. Esta situação é típica para a maioria dos idiomas, o significado da instrução é determinado pelo programa correspondente.

Para simplificar o problema de apresentar informações, consideramos o problema de transmitir informações de um ponto a outro. Esta questão está relacionada à questão da informação sobre conservação. Os problemas de transmissão de informações no tempo e no espaço são idênticos. A Figura 10.1 mostra um modelo padrão para transmissão de informações.



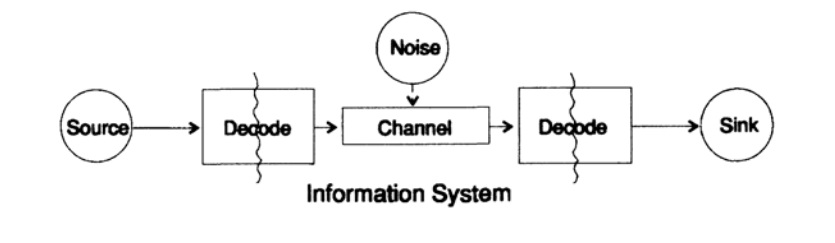Figura 10.1

À esquerda na figura 10.1 está a fonte de informação. Ao considerar o modelo, não nos importamos com a natureza da fonte. Pode ser um conjunto de símbolos do alfabeto, números, fórmulas matemáticas, notas musicais, símbolos com os quais podemos representar movimentos de dança - a natureza da fonte e o significado dos símbolos armazenados nela não fazem parte do modelo de transmissão. Consideramos apenas a fonte de informação; com essa restrição, obtemos uma teoria geral poderosa que pode ser estendida a muitas áreas. É uma abstração de muitos aplicativos.

Quando Shannon criou a teoria da informação no final da década de 1940, acreditava-se que deveria ser chamada de teoria da comunicação, mas ele insistiu no termo informação. Este termo tornou-se uma causa constante de interesse crescente e desapontamento constante na teoria. Os investigadores queriam construir "teorias da informação" inteiras, que degeneraram em uma teoria de um conjunto de caracteres. Voltando ao modelo de transmissão, temos uma fonte de dados que precisa ser codificada para transmissão.

O codificador consiste em duas partes, a primeira parte é chamada de codificador de origem, o nome exato depende do tipo de fonte. Fontes de diferentes tipos de dados correspondem a diferentes tipos de codificadores.

A segunda parte do processo de codificação é chamada de codificação de canal e depende do tipo de canal para transmissão de dados. Assim, a segunda parte do processo de codificação é consistente com o tipo de canal de transmissão. Assim, ao usar interfaces padrão, os dados da fonte são inicialmente codificados de acordo com os requisitos da interface e, em seguida, de acordo com os requisitos do canal de dados usado.

De acordo com o modelo, na Fig. 10.1, o canal de dados é exposto a "ruído aleatório adicional". Todo o ruído no sistema é combinado neste momento. Supõe-se que o codificador aceite todos os caracteres sem distorção e o decodificador desempenhe sua função sem erros. Isso é idealização, mas, para muitos propósitos práticos, é próximo da realidade.

A fase de decodificação também consiste em dois estágios: canal - padrão, padrão - receptor de dados. No final da transferência de dados é transmitida ao consumidor. E, novamente, não estamos considerando como o consumidor interpreta esses dados.

Como observado anteriormente, um sistema de transmissão de dados, por exemplo, mensagens telefônicas, rádio, programas de TV, apresenta dados na forma de um conjunto de números nos registros de um computador. Repito novamente, a transmissão no espaço não é diferente da transmissão no tempo ou do armazenamento de informações. Você possui informações que serão necessárias depois de um tempo e, em seguida, deverão ser codificadas e armazenadas na fonte de armazenamento de dados. Se necessário, as informações são decodificadas. Se o sistema de codificação e decodificação for o mesmo, transmitimos dados através do canal de transmissão sem alterações.

A diferença fundamental entre a teoria apresentada e a teoria usual em física é a suposição de que não há ruído na fonte e no receptor. De fato, ocorrem erros em qualquer equipamento. Na mecânica quântica, o ruído ocorre em qualquer estágio, de acordo com o princípio da incerteza, e não como uma condição inicial; de qualquer forma, o conceito de ruído na teoria da informação não é equivalente a um conceito semelhante na mecânica quântica.
Por definição, consideraremos ainda a forma binária de representação de dados no sistema. Outras formas são processadas de maneira semelhante, por simplicidade, não as consideraremos.

Começamos nossa consideração de sistemas com caracteres codificados de comprimento variável, como no código Morse clássico de pontos e traços, no qual os caracteres que ocorrem com frequência são curtos e os raros são longos. Essa abordagem permite obter alta eficiência de código, mas é importante notar que o código Morse é ternário, não binário, pois contém um espaço entre pontos e traços. Se todos os caracteres no código tiverem o mesmo comprimento, esse código será chamado de código de bloco.

A primeira propriedade necessária óbvia do código é a capacidade de decodificar exclusivamente a mensagem na ausência de ruído, pelo menos essa parece ser a propriedade desejada, embora em algumas situações esse requisito possa ser negligenciado. Os dados do canal de transmissão do receptor se parecem com um fluxo de caracteres de zeros e uns.

Vamos chamar dois caracteres adjacentes de extensão dupla, três caracteres adjacentes de extensão tripla e, no caso geral, se encaminharmos N caracteres, o receptor verá acréscimos ao código base de N caracteres. O receptor, sem saber o valor de N, deve dividir o fluxo em blocos de transmissão. Ou, em outras palavras, o receptor deve poder decompor o fluxo exclusivamente para restaurar a mensagem original.

Considere um alfabeto com um pequeno número de caracteres, geralmente os alfabetos são muito maiores. Alfabetos de idiomas começam de 16 a 36 caracteres, incluindo caracteres maiúsculos e minúsculos, sinais numéricos e pontuação. Por exemplo, na tabela ASCII 128 = 2 ^ 7 caracteres.
Considere um código especial que consiste em 4 caracteres s1, s2, s3, s4

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

Como o receptor deve interpretar a próxima expressão recebida

0011 ?

Como s1s1s4 ou como s2s4 ?

Você não pode dar uma resposta inequívoca a esta pergunta; esse código definitivamente não é decodificado; portanto, é insatisfatório. Código, por outro lado

s1 = 0; s2 = 10; s3 = 110; s4 = 111

decodifica a mensagem de uma maneira única. Pegue uma string arbitrária e considere como o receptor a decodificará. Você precisa construir uma árvore de decodificação De acordo com o formulário da Figura 10.II. String

1101000010011011100010100110 ...

pode ser dividido em blocos de caracteres

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110, ...

de acordo com a seguinte regra para construir uma árvore de decodificação:

Se você estiver no topo da árvore, leia o próximo caractere. Quando você alcança uma folha de uma árvore, converte a sequência em um caractere e volta ao início.

A razão para a existência de uma árvore é que nenhum caractere é um prefixo do outro, então você sempre sabe quando precisa retornar ao início da árvore de decodificação.

É necessário prestar atenção ao seguinte. Em primeiro lugar, a decodificação é um processo estritamente de fluxo, no qual cada bit é examinado apenas uma vez. Em segundo lugar, os protocolos geralmente incluem caracteres que são um marcador do final do processo de decodificação e são necessários para indicar o final de uma mensagem.

Falha ao usar um caractere à direita é um erro comum no design do código. Obviamente, você pode fornecer um modo de decodificação constante; nesse caso, o caractere à direita não é necessário.



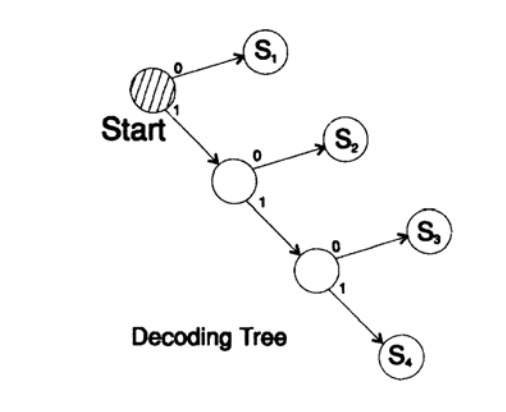Figura 10.II

A próxima pergunta é códigos para decodificação de fluxo (instantânea). Considere o código obtido do anterior exibindo caracteres

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Suponha que obtemos a sequência 011111 ... 111 . A única maneira de decodificar o texto da mensagem é agrupar bits do final de 3 em um grupo e selecionar grupos com um zero à frente de um, depois do qual você pode decodificar. Esse código é decodificado de uma maneira única, mas não instantaneamente! Para decodificação, você deve aguardar o final da transferência! Na prática, essa abordagem elimina a taxa de decodificação (teorema de Macmillan), portanto, é necessário procurar métodos de decodificação instantânea.

Considere duas maneiras de codificar o mesmo caractere, Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

A árvore de decodificação deste método é mostrada na Figura 10.III.



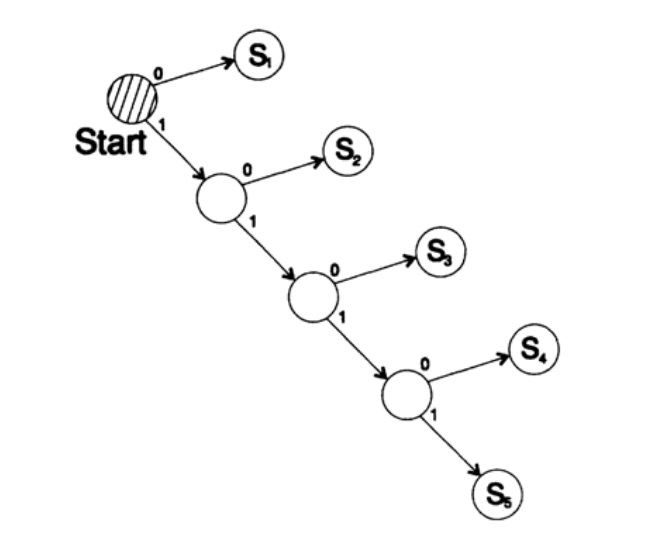Figura 10.III

Segunda via

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111 ,

A árvore de decodificação desse cuidado é mostrada na Figura 10.IV.

A maneira mais óbvia de medir a qualidade do código é o tamanho médio de um conjunto de mensagens. Para isso, é necessário calcular o comprimento do código de cada caractere multiplicado pela probabilidade correspondente de ocorrência de pi. Assim, o comprimento de todo o código é obtido. A fórmula para o comprimento médio L do código para um alfabeto de q caracteres é a seguinte



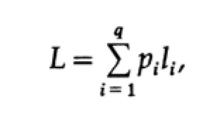
onde pi é a probabilidade de ocorrência do símbolo si, li é o comprimento correspondente do símbolo codificado. Para um código eficiente, o valor de L deve ser o menor possível. Se P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 e p5 = 1/16, então para o código # 1 obtemos o valor do comprimento do código



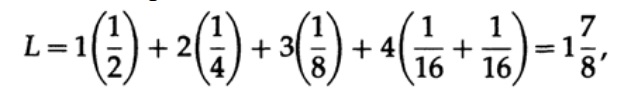
E para o código # 2



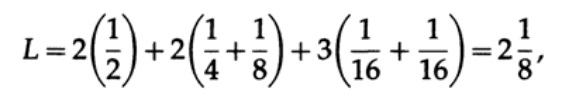
Os valores obtidos indicam a preferência do primeiro código.
Se todas as palavras do alfabeto tiverem a mesma probabilidade de ocorrência, o segundo código será mais preferível. Por exemplo, com pi = 1/5, comprimento do código # 1



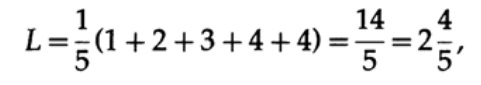
e comprimento do código # 2



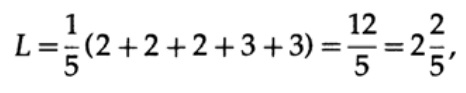
este resultado mostra uma preferência por 2 códigos. Assim, ao desenvolver um código “bom”, é necessário considerar a probabilidade de ocorrência de caracteres.



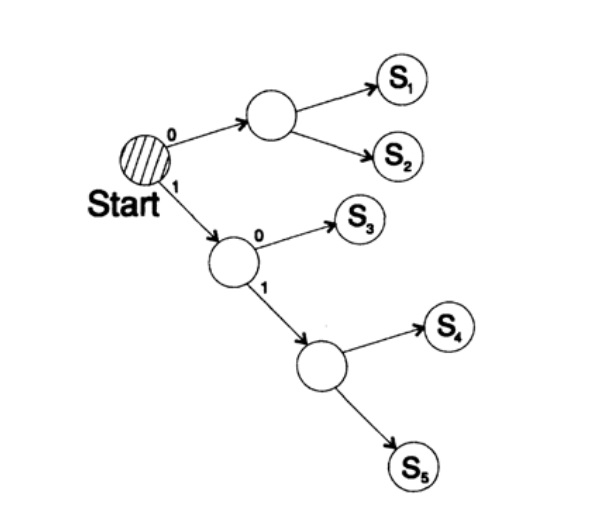Figura 10.IV



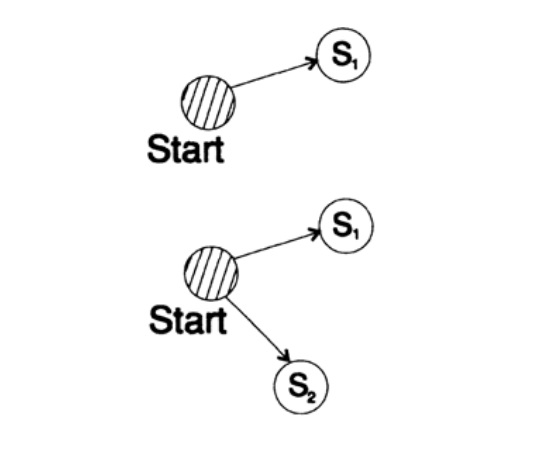Figura 10.V

Considere a desigualdade de Kraft, que determina o valor limite do comprimento do código do símbolo li. Na base 2, a desigualdade é representada como



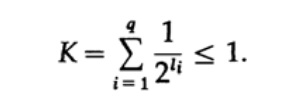
Essa desigualdade sugere que o alfabeto não pode ter muitos caracteres curtos, caso contrário, a soma será bastante grande.

Para provar a desigualdade de Kraft para qualquer código decodificado rápido e único, construímos uma árvore de decodificação e aplicamos o método de indução matemática. Se uma árvore tem uma ou duas folhas, como mostra a Figura 10.V, a desigualdade é sem dúvida verdadeira. Além disso, se a árvore tiver mais de duas folhas, dividimos a árvore de m longo em duas subárvores. De acordo com o princípio da indução, assumimos que a desigualdade é verdadeira para cada ramo de altura m -1 ou menos. De acordo com o princípio da indução, aplicando desigualdade a cada ramo. Indique os comprimentos dos códigos das ramificações K 'e K' '. Ao combinar dois ramos de uma árvore, o comprimento de cada um aumenta em 1; portanto, o comprimento do código consiste nas somas K '/ 2 e K' '/ 2,



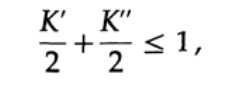
o teorema é provado.

Considere a prova do teorema de Macmillan. Aplicamos a desigualdade de Kraft aos códigos de decodificação sem fio. A prova é baseada no fato de que, para qualquer número K> 1, a enésima potência do número é obviamente mais do que uma função linear de n, onde n é um número bastante grande. Elevamos a desigualdade de Kraft ao enésimo poder e apresentamos a expressão como uma soma



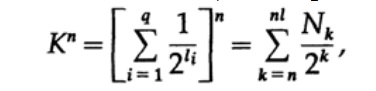
onde Nk é o número de caracteres de comprimento k, a soma começa com o comprimento mínimo da enésima representação do caractere e termina com o comprimento máximo nl, onde l é o comprimento máximo do caractere codificado. Da exigência de decodificação exclusiva, segue-se isso. O valor é apresentado como



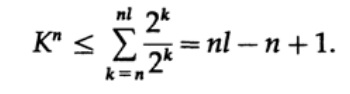
Se K> 1, é necessário estabelecer n grande o suficiente para que a desigualdade se torne falsa. Portanto, k <= 1; O teorema de Macmillan está provado.

Considere alguns exemplos da aplicação da desigualdade de Kraft. Pode existir um código decodificado exclusivo com comprimentos 1, 3, 3, 3? Sim desde



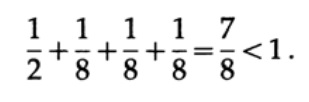
E quanto aos comprimentos 1, 2, 2, 3? Calcular de acordo com a fórmula



Desigualdade violada! Existem muitos caracteres curtos neste código.

Os códigos de vírgula são códigos que consistem em caracteres 1, terminando com um caractere 0, com exceção do último caractere que consiste em todos. Um dos casos especiais é o código.

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5 = 11111.

Para este código, obtemos a expressão para a desigualdade de Kraft



Nesse caso, alcançamos a igualdade. É fácil ver que, para códigos de pontos, a desigualdade de Kraft degenera em igualdade.

Ao criar um código, você precisa prestar atenção à quantidade de Kraft. Se o valor Kraft começar a exceder 1, esse é um sinal sobre a necessidade de incluir um caractere de tamanho diferente para reduzir o tamanho médio do código.

Deve-se notar que a desigualdade da Kraft não significa que esse código seja decodificável exclusivamente, mas que existe um código com caracteres de tamanho igual que é decodificado exclusivamente. Para criar um código decodificado exclusivo, você pode atribuir o comprimento correspondente em bits li com um número binário. Por exemplo, para os comprimentos 2, 2, 3, 3, 4, 4, 4, 4, obtemos a desigualdade de Kraft



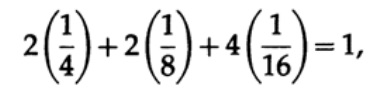
Portanto, pode existir um código de fluxo decodificado exclusivo.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

Quero prestar atenção ao que realmente acontece quando trocamos idéias. Por exemplo, neste momento, quero transferir a ideia da minha cabeça para a sua. Pronuncio algumas palavras através das quais, como acredito, você pode entender (entender) essa ideia.

Mas quando um pouco mais tarde você quiser transmitir essa idéia ao seu amigo, quase certamente proferirá palavras completamente diferentes. De fato, o significado ou significado não está incluído em nenhuma palavra específica. Usei algumas palavras e você pode usar palavras completamente diferentes para transmitir a mesma ideia. Assim, palavras diferentes podem transmitir a mesma informação. Porém, assim que você disser ao seu interlocutor que não entende a mensagem, em geral o interlocutor selecionará um conjunto diferente de palavras, a segunda ou até a terceira, para transmitir o significado. Portanto, as informações não são incluídas em um conjunto de palavras específicas. Assim que você recebe essas ou aquelas palavras, trabalha muito ao traduzir as palavras na ideia que o interlocutor deseja transmitir a você.

Aprendemos a selecionar palavras para se adaptar ao interlocutor. Em certo sentido, escolhemos palavras que correspondem aos nossos pensamentos e ao nível de ruído no canal, embora essa comparação não reflita com precisão o modelo que eu uso para representar o ruído no processo de decodificação. Nas grandes organizações, um problema sério é a incapacidade do interlocutor de ouvir o que outra pessoa disse. Em cargos seniores, os funcionários ouvem o que "querem ouvir". Em alguns casos, você precisa se lembrar disso quando subir a carreira. A apresentação de informações de forma formal é um reflexo parcial dos processos de nossas vidas e encontrou ampla aplicação muito além dos limites das regras formais em aplicativos de computador.

Para continuar ...

Quem quiser ajudar na tradução, layout e publicação do livro - escreva em um e-mail pessoal ou envie um e-mail para magisterludi2016@yandex.ru

A propósito, também lançamos a tradução de outro livro interessante - “A Máquina dos Sonhos: a história da revolução dos computadores” )