Redes Neurais Capsulares

Em 2017, Jeffrey Hinton (um dos fundadores da abordagem de erro de propagação traseira) publicou um artigo descrevendo redes neurais capsulares e propondo um algoritmo para roteamento dinâmico entre cápsulas para ensinar a arquitetura proposta.

As redes neurais convolucionais clássicas têm desvantagens. A representação interna de dados de redes neurais convolucionais não leva em consideração hierarquias espaciais entre objetos simples e complexos. Portanto, se os olhos, nariz e lábios de uma rede neural convolucional são exibidos aleatoriamente na imagem, esse é um sinal claro da presença de um rosto. E a rotação do objeto afeta a qualidade do reconhecimento, enquanto o cérebro humano resolve facilmente esse problema.


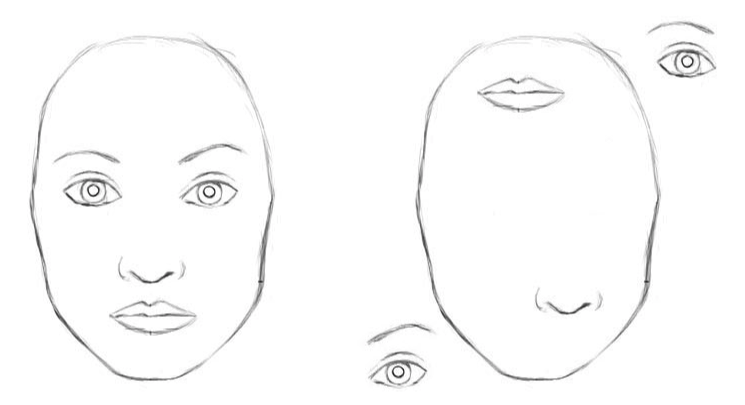
Para uma rede neural convolucional, 2 imagens são semelhantes [2]


Milhares de exemplos serão necessários para treinar o reconhecimento de objetos de vários ângulos da CNN.


As redes de cápsulas reduzem o erro de reconhecimento de um objeto de outro ângulo em 45%.

Cápsulas de prescrição

As cápsulas encapsulam informações sobre o estado da função, encontrado em forma vetorial. Cápsulas codificam a probabilidade de detectar um objeto como o comprimento do vetor de saída. O estado da função detectada é codificado como a direção na qual o vetor aponta ("parâmetros de criação da instância"). Portanto, quando a função detectada se move pela imagem ou o estado da imagem muda, a probabilidade permanece inalterada (o comprimento do vetor não muda), mas a orientação muda.

Imagine que uma cápsula detecta um rosto em uma imagem e produz um vetor 3D de 0,99. Em seguida, mova o rosto na imagem. O vetor girará em seu espaço, representando um estado variável, mas seu comprimento permanecerá fixo porque a cápsula está confiante de que detectou um rosto.



Diferenças entre cápsulas e neurônios. [2]

Um neurônio artificial pode ser descrito em três etapas:

1. ponderação escalar dos escalares de entrada
2. soma dos escalares de entrada ponderados
3. transformação escalar não linear.

A cápsula possui as formas vetoriais das três etapas acima, além da nova fase da transformação afim da entrada:

1. multiplicação matricial de vetores de entrada
2. ponderação escalar de vetores de entrada
3. soma dos vetores de entrada ponderados
4. não linearidade do vetor.

Outra inovação introduzida no CapsNet é uma nova função de ativação não linear que pega um vetor e depois “distribui” seu comprimento não mais que 1, mas não muda de direção.



O lado direito da equação (retângulo azul) dimensiona o vetor de entrada para que o vetor tenha um comprimento de bloco e o lado esquerdo (retângulo vermelho) executa uma escala adicional.

O design da cápsula é baseado na construção de um neurônio artificial, mas o estende a uma forma vetorial para fornecer recursos representativos mais poderosos. Os pesos da matriz também são introduzidos para codificar relacionamentos hierárquicos entre recursos de diferentes camadas. A equivalência da atividade neural é alcançada em relação às mudanças nos dados de entrada e invariância nas probabilidades de detectar sinais.

Roteamento dinâmico entre cápsulas

O algoritmo de roteamento dinâmico [1].

A primeira linha diz que esse procedimento utiliza cápsulas no nível inferior le suas saídas u_hat, bem como o número de iterações de roteamento r. A última linha diz que o algoritmo produzirá a saída de uma cápsula de nível superior v_j.

A segunda linha contém um novo coeficiente b_ij, que não vimos antes. Esse coeficiente é um valor temporário que será atualizado iterativamente e, após a conclusão do procedimento, seu valor será armazenado em c_ij. No início do treinamento, o valor de b_ij é inicializado em zero.

A linha 3 diz que as etapas 4-7 serão repetidas r vezes.
A etapa na linha 4 calcula o valor do vetor c_i, que é todos os pesos de roteamento para a cápsula inferior i.

Depois que os pesos c_ij forem calculados para as cápsulas do nível mais baixo, vá para a linha 5, onde examinamos as cápsulas de um nível mais alto. Esta etapa calcula uma combinação linear de vetores de entrada ponderados usando os coeficientes de roteamento c_ij definidos na etapa anterior.

Em seguida, na linha 6, os vetores da última etapa passam por uma transformação não linear, que garante a direção do vetor, mas seu comprimento não deve exceder 1. Essa etapa cria o vetor de saída v_j para todos os níveis mais altos da cápsula. [2]
A idéia básica é que a similaridade entre entrada e saída seja medida como o produto escalar entre a entrada e a saída da cápsula e, em seguida, o coeficiente de roteamento seja alterado. A melhor prática é usar três iterações de roteamento.

Conclusão

As redes neurais capsulares são uma arquitetura promissora de redes neurais que aprimora o reconhecimento de imagens com diferentes ângulos e estrutura hierárquica. As redes neurais capsulares são treinadas usando roteamento dinâmico entre cápsulas. As redes de cápsulas reduzem o erro de reconhecimento de um objeto de um ângulo diferente em 45% em comparação à CNN.