O que aconteceu com o paradoxo de Fermi

O paradoxo de Fermi é que a probabilidade de uma civilização extraterrestre é geralmente estimada bastante alta e não há nada para ver sinais de sua existência. Recentemente, uma pré - impressão de Sanders e co-autores de “Dissolver o paradoxo de Fermi” apareceu no arxiv, que eles já interpretaram como cancelando esse paradoxo (verdadeiro), tagarelice inativa na ausência de dados (bastante verdadeiro, mas verdadeiro para o paradoxo de Fermi em geral, e não apenas para este artigo) e como evidência da inexistência de alienígenas e / ou baixo L (mentira). Neste artigo, tentaremos descobrir o que realmente contém a pré-impressão.

Qual é o problema?

Primeiro de tudo, a própria equação de Drake. É apresentado no KDPV; o último fator é uma piada, e o resto deve ser entendido da seguinte forma: no universo observável (ou em nossa galáxia ou em qualquer outro volume de espaço) $$ estrelas. Toda estrela com probabilidade $$ tem planetas. É provável que cada um desses planetas $$ localizado na zona Goldilocks, possui uma composição química adequada, etc. Em todo planeta que é potencialmente capaz de sustentar a vida com probabilidade $$ (por unidade de tempo) surge uma vida que é provável $$ atinge razoabilidade e probabilidade $$ entra em contato. E finalmente, qualquer espécie inteligente que surgir existe $$ anos desde o nascimento até a extinção. Se você multiplicar tudo isso, obtém o número de espécies inteligentes nessa área.

O tempo entre a origem da mente e o surgimento de uma civilização perceptível a distâncias interestelares é negligenciado. No caso da Terra, por exemplo, bilhões de anos passaram da aparência do planeta à aparência da vida e da aparência da vida à aparência da espécie Homo sapiens . O progresso tecnológico é incomparavelmente mais rápido - o surgimento do Homo sapiens da mensagem de Arecibo separa menos de dez milhões de anos. A colonização interestelar ainda não começou, mas este também é o pior caso de alguns milhões de anos. Comparado com os estágios pré-tecnológicos - dentro da margem de erro.

O que, para dizer com mais tato, é bastante alto . Da ordem de magnitude para o número de estrelas e a probabilidade de ter planetas com até 200 ordens de magnitude (duzentas ordens de magnitude, as estimativas diferem em $$ vezes) para a probabilidade de abiogênese. Esse trabalho ingrato é avaliar probabilidades a partir de uma única observação. No entanto, os cientistas publicaram várias estimativas $$ e na maioria das vezes chegou à conclusão de que $$ e até $$ . De fato, qual é o paradoxo de Fermi: de acordo com nossas melhores estimativas, deve haver outras raças inteligentes na galáxia e não havia evidências confiáveis ​​de sua existência.

O problema, obviamente, não está na galáxia: se as estimativas diferem da realidade observada, pior ainda para as estimativas. Qualquer um dos parâmetros está superestimado ( e Deus nos abençoe, se for L ), ou de alguma forma pensamos incorretamente. Sandberg e colaboradores estão apenas defendendo a versão mais recente.

E como contar corretamente?

Parece multiplicar alguns números reais - não o binômio de Newton. O problema é que, em tal situação, a multiplicação de números se baseia na suposição de que eles são precisamente conhecidos por nós. Como vimos acima, essa suposição está muito longe da realidade.

Considere um exemplo simplificado: deixe a equação de Drake ter nove parâmetros e todos os nove serem uniformemente distribuídos no intervalo $$ . A melhor estimativa de pontos para cada um desses parâmetros é 0,1 e seu produto fornece uma probabilidade de uma civilização por bilhão de estrelas. Na galáxia de $$ algo em torno de 100 civilizações deve aparecer nas estrelas e a probabilidade de isso nunca acontecer - $$ . Tais probabilidades são geralmente ilustradas com frases como "se todo átomo em <algo muito grande como o sistema solar> por <algum tempo muito longo como sua idade>". O que, nesse caso, parece bastante apropriado, mas, na verdade, é impossível não rejeitar uma hipótese tão nula. O paradoxo de Fermi se eleva a toda sua altura.

Se não usarmos estimativas pontuais, e para cada parâmetro tomarmos um valor aleatório do intervalo correspondente, a galáxia estará vazia em 21,45% das simulações. O fato de algo ter acontecido com uma probabilidade de pouco mais de um quinto não é de forma alguma um paradoxo. É um pouco menos provável que um par de reis vença todas as outras mãos em uma mesa de 9 jogadores , e com os par de reis eu pessoalmente faço all-in na primeira oportunidade.

A mesma lógica pode ser aplicada a estimativas reais dos parâmetros da equação de Drake. Se você coletá-los da literatura e executar a simulação, obtém a seguinte imagem:



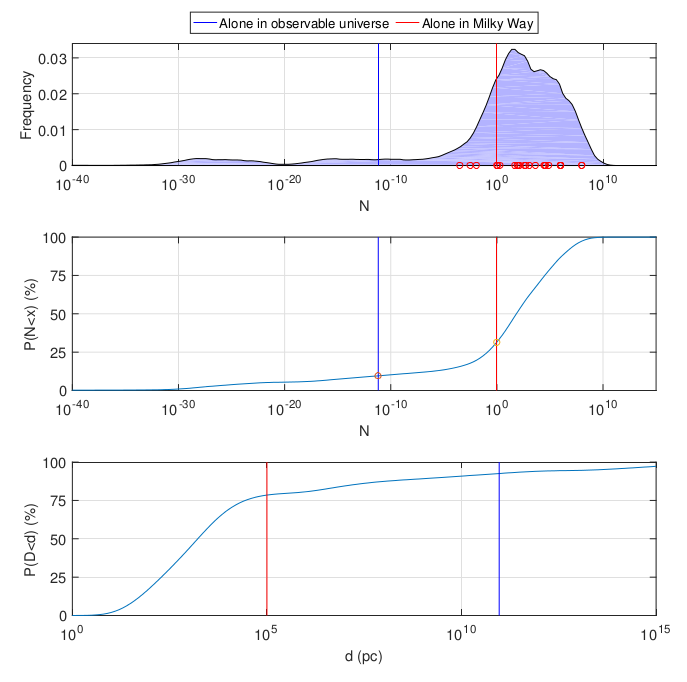
De cima para baixo: a função densidade de probabilidade para o número de civilizações em nossa galáxia, a densidade cumulativa de distribuição para ela, a densidade cumulativa de distribuição da distância até a civilização observável mais próxima em parsecs. Tudo está em uma escala logarítmica. As linhas vermelhas e azuis indicam a probabilidade de sermos a única civilização em nossa galáxia e no universo observável. Círculos no gráfico superior - classificações literárias normalizadas $$ .

No geral, o resultado é bastante otimista: a maior densidade de probabilidade recai na multiplicidade de civilizações (média 53 milhões, mediana 100). Mas, para os propósitos do paradoxo de Fermi, os números são aproximadamente os mesmos de um exemplo simplificado: com uma probabilidade de vinte por cento ou algo assim, a Via Láctea contém apenas uma civilização (a nossa). A propósito, uma consequência bastante contra-intuitiva: a probabilidade de que a Via Láctea, sem contar a Terra , contenha exatamente uma civilização (exceto a nossa) é praticamente a mesma.

Em vez de obter estimativas de parâmetros diretamente da literatura, as distribuições podem ser construídas e calculadas analiticamente. Uma gama de estimativas é feita em uma ordem de magnitude e cada parâmetro é considerado log-normal ou log-distribuído uniformemente no intervalo correspondente. O resultado muda um pouco para a esquerda, mas o significado é o mesmo:



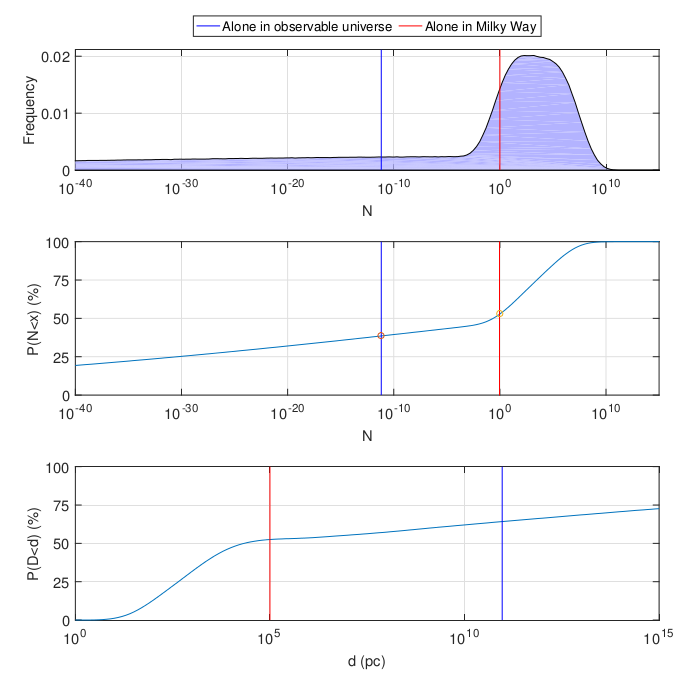
O que tudo isso significa? A resposta correta para a pergunta "existe vida no universo ou não existe" ainda "não sei". Como as estatísticas bayesianas agradavelmente elegantes custam pouco na ausência de dados experimentais. A resposta à pergunta “Quanto devemos nos surpreender com o que foi observado mudou $$ " Costumava ser "muito forte, então ou a vida é uma coisa muito rara, ou todos nós morreremos em uma guerra nuclear ou algo assim ", e agora se tornou "bem, em princípio, não é muito provável, mas nada de extraordinário". A probabilidade de uma guerra nuclear e / ou encontro com um dinossauro nos alienígenas de Nevsky caiu apenas no sentido bayesiano: temos um pouco menos de certeza de que isso acontecerá. Se esses eventos realmente acontecem ou não, depende dos fatores do mundo real (aproximadamente Putin, Trump e Zorblaks, o Comedor Galáctico), e não da matemática usada para discuti-los.