Auto codificadores e forte inteligência artificial

A teoria dos codificadores automáticos e dos modelos de geração foi recentemente desenvolvida com seriedade, mas alguns trabalhos são dedicados a como usá-los em problemas de reconhecimento. Ao mesmo tempo, a propriedade dos auto-codificadores para obter um modelo de dados paramétricos ocultos e as conseqüências matemáticas disso permitem associá-los aos métodos de tomada de decisão bayesiana.

O artigo propõe um aparelho matemático original "um conjunto de codificadores automáticos com um espaço latente comum", que permite extrair conceitos abstratos dos dados de entrada e demonstra a capacidade de "aprendizado único". Além disso, ele pode ser usado para superar muitos dos problemas fundamentais dos algoritmos modernos de aprendizado de máquina baseados em redes multicamadas e na abordagem de "aprendizado profundo".

Antecedentes

As redes neurais artificiais, treinadas usando o mecanismo de propagação reversa de erros, quase substituíram outras abordagens em muitos problemas de reconhecimento e estimativa de parâmetros. Mas eles têm várias desvantagens que, ao que parece, não podem ser eliminadas sem uma revisão séria da abordagem:

1. extrema instabilidade na entrada de dados não encontrados na amostra de treinamento (inclusive no caso de ataques adversos)
   
   
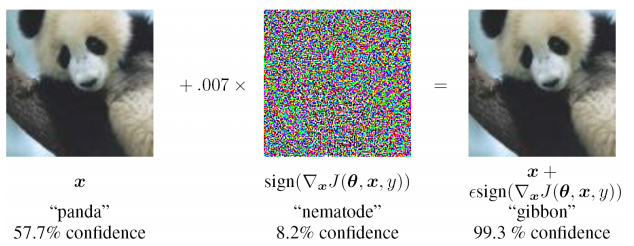
2. é difícil avaliar a origem do problema e treinar novamente localmente em um dos níveis (você só precisa suplementar a amostra e treinar novamente), ou seja, problema da caixa preta
3. não é fornecida a possibilidade de diferentes interpretações da mesma informação de entrada, a natureza estatística dos dados observados é ignorada
   
   

Estando envolvido na solução de problemas aplicados e contando com uma série de trabalhos existentes, proponho uma abordagem notavelmente diferente das existentes, elimine várias deficiências e é aplicável à solução de problemas aplicados em várias áreas do aprendizado de máquina.

Codificador automático para estimar a densidade de distribuição

Na teoria da tomada de decisão, um lugar muito importante é ocupado pela densidade de distribuição (ou função de distribuição) de variáveis ​​aleatórias. É necessário ter estimativas das funções de distribuição para calcular o risco posterior.

Acontece que os codificadores automáticos são muito naturais para avaliar as funções de distribuição. Isso pode ser explicado da seguinte forma: o conjunto de dados de treinamento é determinado pela densidade de sua distribuição. Quanto maior a densidade de exemplos de treinamento em torno de um ponto local no espaço de entrada, melhor o codificador automático reconstrói o vetor de entrada nesse local no espaço. Além disso, dentro do autoencodificador há um vetor de representação latente dos dados de entrada (geralmente de baixa dimensão) e, se os dados são projetados no espaço latente em uma área que não era usada anteriormente no treinamento, não havia nada semelhante na amostra de treinamento.

Há vários trabalhos fechados e um tanto isolados:

1. Alain, G. e Bengio, Y. O que os auto-codificadores regularizados aprendem com a distribuição de geração de dados. 2013.
2. Kamyshanska, H. 2013. Na pontuação do autoencoder
3. Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservação de codificadores automáticos desatados

O primeiro justifica que o resultado da reconstrução de Denoising dos auto-codificadores está relacionado à função de densidade de probabilidade dos dados de entrada, mas várias restrições são impostas aos auto-codificadores. O segundo contém requisitos suficientes para o codificador automático - os pesos do codificador e decodificador devem ser "conectados", ou seja, a matriz de peso da camada do codificador é a matriz transposta do decodificador. No último trabalho, as condições necessárias e suficientes para o fato de o codificador automático estar associado a uma densidade de probabilidade são mais completamente investigadas.

Esses trabalhos substanciam estritamente a base teórica para a relação dos auto-codificadores com a densidade de distribuição dos dados de treinamento. Em problemas aplicados, uma análise tão séria muitas vezes não é necessária; portanto, uma abordagem ligeiramente diferente será dada abaixo que nos permitirá estimar a função de densidade de probabilidade dos dados de entrada devido a um autoencoder previamente treinado.

Exemplo MNIST

Em trabalhos ainda anteriores, foi proposta a idéia empírica de que, para o problema de classificação, é possível treinar auto-codificadores pelo número de aulas (ensinando cada uma delas apenas na subamostra correspondente). E escolha como resposta a classe e o codificador automático que oferecem a discrepância mínima entre a imagem de entrada e a reconstruída. Não foi difícil verificar o MNIST: treinar 10 codificadores automáticos (para cada dígito), calcular a precisão e comparar com um modelo multicamada semelhante do classificador.

Scripts para treinamento e teste no git (train_ae.py, calc_codes.py, calc_acc.py)

Arquitetura e número de pesos:



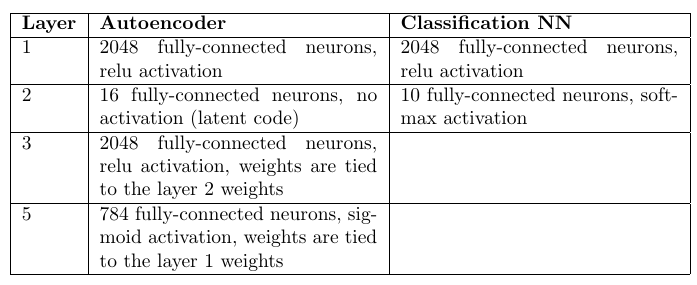
Codificadores automáticos: 98,6%
Classificador de perceptron multicamadas: 98,4%

Um leitor atento perceberá que havia 10 vezes mais pesos nos codificadores automáticos (pelo número). No entanto, um aumento de 10 vezes no número de pesos na camada oculta em um perceptron de multicamadas apenas piora as estatísticas.

Obviamente, as redes de convolução fornecem uma precisão muito maior, mas a tarefa era apenas comparar abordagens, todas as outras coisas sendo iguais.

Como resultado, pode-se notar que a abordagem com codificadores automáticos é bastante competitiva com redes totalmente conectadas. E embora demore muito mais tempo para otimizar pesos, ele tem uma vantagem importante: a capacidade de detectar anomalias nos dados de entrada. Se nenhum dos codificadores automáticos conseguiu reconstruir com precisão a imagem de entrada, podemos afirmar que foi inserida uma imagem anômala que não ocorreu na amostra de treinamento. A rigor, você pode reconstruir uma imagem não a partir da amostra de entrada, mas o que fazer nessa situação será mostrado posteriormente.

Considere um único codificador automático

É possível, de uma maneira ligeiramente diferente da dos trabalhos acima, realizar uma análise qualitativa da relação entre a densidade de probabilidade dos dados de entrada p (x) e a resposta do autoencoder.

Codificador automático - uso seqüencial da função de codificador $$$z = g (x)$ e decodificador $$$x ^ * = f (z)$ onde $$$x$ É o vetor de entrada e $$$z$ - desempenho latente. Em algum subconjunto de entrada (geralmente próximo ao treinamento) $$$x ^ * = x + n = f (g (x))$ onde $$$n$ discrepância. Aceitamos a discrepância pelo ruído de Gausovsky (seus parâmetros podem ser estimados após o treinamento do autoencoder). Como resultado, são feitas várias suposições bastante fortes:

1) discrepância - ruído gaussiano
2) o codificador automático já está “treinado” e funcionando

Mas, mais importante, quase nenhuma restrição será imposta ao próprio codificador automático.

Além disso, uma estimativa qualitativa da densidade de probabilidade p (x) pode ser obtida, com base nas quais várias conclusões que são muito importantes no futuro podem ser feitas.

Pontuação P (x) para um único codificador automático

Densidade de distribuição para $$$x \ em X$ e $$$z \ em Z$ relacionados da seguinte forma:

$$

$$p (x) = \ int_ {z} p (x | z) p (z) dz \; \; \; (1)$$

Precisamos obter a conexão p (x) ep (z). Para alguns codificadores automáticos, p (z) é definido no estágio de treinamento; para outros, é ainda mais fácil obter p (z) devido à menor dimensão Z.

A distribuição de densidade do n residual é conhecida, o que significa:

$$

$$p (n) = const \ times exp (- \ frac {(xf (z)) ^ T (xf (z))} {2 \ sigma ^ 2}) = p (x | z) \; \; ( 2)$$

$$$(x-f (z)) ^ T (x-f (z))$ É a distância entre x e sua projeção x *. Em algum momento z *, essa distância atingirá o mínimo. Neste ponto, as derivadas parciais do argumento do expoente na fórmula (2) em relação a $$$z_i$ (Eixo Z) será zero:

$$

$$0 = \ frac {\ parcial f (z ^ *)} {\ parcial z_i} ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ frac {\ parcial f (z ^ * )} {\ z_i parcial}$$

Aqui $$$\ frac {\ parcial f (z ^ *)} {\ parcial z_i} ^ T (x-f (z ^ *))$ escalar então:

$$

$$0 = \ frac {\ parcial f (z ^ *)} {\ parcial z_i} ^ T (x-f (z ^ *)) \; \; \; (3)$$

A escolha do ponto z *, onde a distância $$$(x-f (z)) ^ T (x-f (z))$ mínimo devido ao processo de otimização do codificador automático. Durante o treinamento, é o resíduo quadrático que é minimizado (como regra): $$$\ min \ limits _ {\ theta, \ forall x \ in X train} L2_ {norm} ({x-f_ \ theta (g_ \ theta (x))})$ onde $$$\ theta$ - o peso do codificador. I.e. após o treinamento, g (x) tende a z *.

Nós também podemos expandir $$$f (z)$ em uma série de Taylor (até o primeiro termo) em torno de z *:

$$

$$f (z) = f (z ^ *) + \ nabla f (z ^ *) (z-z ^ *) + o ((z-z ^ *))$$

Então, agora a equação (2) se torna:

$$

$$p (x | z) \ approx const \ times exp (- \ frac {((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *)) ^ T ((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) =$$

$$

$$= const \ times exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) exp (- \ frac {(\ nabla f (z ^ *) (zz ^ *)) ^ T (\ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) \ vezes$$

$$

$$\ times exp (- \ frac {(\ nabla f (z ^ *)) ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ nabla f (z ^ *)) (zz ^ *)} {2 \ sigma ^ 2})$$

Observe que o último fator é 1 devido à expressão (3). O primeiro fator pode ser removido pelo sinal da integral (não contém z) em (1). E também suponha que p (z) seja uma função suficientemente suave e não mude muito na vizinhança de z *, ou seja, substitua p (z) -> p (z *).

Depois de todas as suposições, a integral (1) tem a estimativa:

$$

$$p (x) = const \ times p (z ^ *) exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) \ int_ {z} exp (- (zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)) dz, \; \; \; z ^ * = g (x)$$

onde $$$W (x) = \ frac {\ nabla f (z ^ *)} {\ sigma}, z ^ * = g (x)$
A última integral é a integral de Euler-Poisson n-dimensional:

$$

$$\ int_ {z} exp (- \ frac {(zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)} {2}) dz = \ sqrt {\ frac {1} {det ( W (x) ^ TW (x) / 2 \ pi)}}$$

Como resultado, obtivemos a estimativa final p (x):

$$

$$p (x) = const \ times exp (- \ frac {(xf (z ^ * *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) p (z ^ *) \ sqrt {\ frac {1} {det (W (x) ^ TW (x) / 2 \ pi)}}, z ^ * = g (x) \; \; \; (4)$$

Toda essa matemática foi necessária para mostrar que p (x) depende de três fatores:

• A distância entre o vetor de entrada e sua reconstrução, quanto pior for restaurada, menor p (x)
• Densidades de probabilidade p (z *) em z * = g (x)
• Normalização da função p (z) no ponto z *, calculado para o autoencoder a partir de derivadas parciais da função f

E a partir da constante de normalização, que posteriormente será responsável pela probabilidade a priori de escolher um codificador automático para descrever os dados de entrada.

Apesar de todas as suposições, o resultado foi muito significativo e útil do ponto de vista dos cálculos.

Classificação de parâmetros ou procedimento de classificação

Agora você pode descrever com mais precisão o procedimento de classificação usando um conjunto de codificadores automáticos:

1. Treinamento de codificadores automáticos independentes para cada classe na saída correspondente
2. Cálculo da matriz W para cada autoencoder
3. Pontuação P (z) para cada codificador automático

E para cada vetor de entrada você pode avaliar agora $$$p (x | classe)$ pelo número de classes. E essa será a função de probabilidade necessária para a tomada de decisões dentro da estrutura da regra bayesiana para a tomada de decisões.

Da mesma forma, parâmetros desconhecidos também podem ser estimados dividindo o espaço do parâmetro em valores discretos, treinando seu próprio codificador automático para cada valor. E então, com base na melhor pontuação bayesiana, escolha o valor que fornece a função de máxima probabilidade.

Aqui vale a pena notar que, formalmente, o problema de estimar p (z) não é mais simples do que estimar p (x). Mas, na prática, não é assim. O espaço Z geralmente possui uma dimensão muito menor ou a distribuição geralmente é definida ao otimizar os pesos do codificador automático.

A ideia de combinar o espaço latente dos auto-codificadores

Há uma curiosa interpretação proposta por Alexei Redozubov e descrita nos seguintes artigos:

1. Uma arquitetura de rede neural artificial baseada em transformações de contexto em minicolunas corticais. Vasily Morzhakov, Alexey Redozubov
2. Memória holográfica: Um novo modelo de processamento de informações por microcircuitos neurais. Alexey Springer Redozubov
3. Redes não neurais. Morzhakov V.

As informações podem ter uma interpretação completamente diferente em diferentes contextos. O modelo de um "conjunto de codificadores automáticos" ecoa essa idéia proposta. Qualquer codificador automático é um modelo latente de dados de entrada no mesmo contexto (uma classe ou outros parâmetros fixos), ou seja, o vetor latente é uma interpretação e cada codificador automático é um contexto. Após o recebimento das informações de entrada, elas são consideradas em cada contexto (por cada codificador automático) e é selecionado o contexto que provavelmente leva em consideração os modelos existentes em cada codificador automático.

O próximo passo razoável é permitir a interseção de interpretações em diferentes contextos. I.e. durante o treinamento, geralmente sabemos que a interpretação permanece a mesma, mas a forma de apresentação (contexto) muda. Por exemplo, a orientação de um objeto muda, mas o objeto permanece o mesmo. O vetor da descrição do objeto deve ser preservado e a orientação ao contexto é alterada.

Então, se dermos uma olhada na fórmula (4), o fator p (z) será estimado para todo o conjunto de auto-codificadores, e não para cada um separadamente. A interpretação (vetor latente) terá uma distribuição comum. Para um pequeno número de codificadores automáticos, isso pode não ter um papel significativo, mas em uma tarefa real esse número pode ser enorme. Por exemplo, se você definir um contexto para cada orientação possível de um objeto 3D, pode haver centenas de milhares deles. Agora, cada exemplo apresentado para treinamento em qualquer contexto formará uma distribuição p (z).

Intercambiabilidade de interpretação e contexto

No problema aplicado, surge imediatamente a pergunta: o que atribuir por interpretação e o que por contexto? Contexto e interpretação podem ser facilmente trocados e ninguém exclui a possibilidade do funcionamento paralelo simultâneo de um par de "conjuntos de autoencodificadores".

Para maior clareza, você pode oferecer este exemplo:

A imagem de entrada contém os rostos das pessoas.

1. orientação contextual. Então, para reconstruir a imagem de entrada, não temos “interpretação” suficiente - um código que identifica uma pessoa, que conterá uma descrição do rosto, penteado e iluminação. Durante o treinamento, precisaremos apresentar a mesma face de lados diferentes, “congelando” o código latente e alterando a orientação.
2. contexto - tipo de rosto, iluminação, penteado. Então, para a reconstrução da imagem de entrada, não temos a orientação da face. Durante o treinamento, será necessário mostrar rostos diferentes em diferentes condições de iluminação, mas com a mesma orientação.

A decisão bayesiana ideal no primeiro caso será tomada em relação à orientação da face e no segundo - seu tipo. Presumivelmente, a primeira opção fornecerá melhor precisão na orientação e a segunda avaliará com mais precisão de quem era a face.

Aprendendo um conjunto de codificadores automáticos com espaço latente compartilhado

No treinamento, precisamos saber como uma entidade em termos de significado se parece em diferentes contextos. Por exemplo, se falamos sobre a imagem dos números e a orientação ao contexto, esquematicamente esse treinamento cruzado se parece com o seguinte:



O codificador de um codificador automático é usado e, em seguida, o código latente é decodificado pelo decodificador de outro codificador automático. A função de perda de aprendizado permanece padrão. É interessante que, se o codificador automático for selecionado simétrico (ou seja, os pesos do codificador e do decodificador estiverem conectados), em cada iteração todos os pesos dos dois codificadores automáticos serão otimizados.

O mais conveniente para esse treinamento complicado foi o PyTorch, que permite criar esquemas bastante complexos para a propagação de erros, inclusive dinâmicos.

As etapas de aprendizado padrão de cada codificador automático alternam com a iteração do treinamento cruzado. Como resultado, todos os codificadores automáticos têm um espaço latente comum ou "interpretação" em diferentes contextos.

É muito importante que, como resultado dessa análise, possamos dividir as informações de entrada em "contexto" e "interpretação".

Exemplo de treinamento

Considere um exemplo bastante simples baseado no MNIST, que ajudará a demonstrar o princípio de treinar auto-codificadores com um espaço latente comum. Como resultado, este exemplo demonstrará a formação do conceito abstrato de “cubo” usando o mecanismo descrito no artigo.

Os números do MNIST são plotados na borda do cubo e ele gira em torno de um de seus eixos:



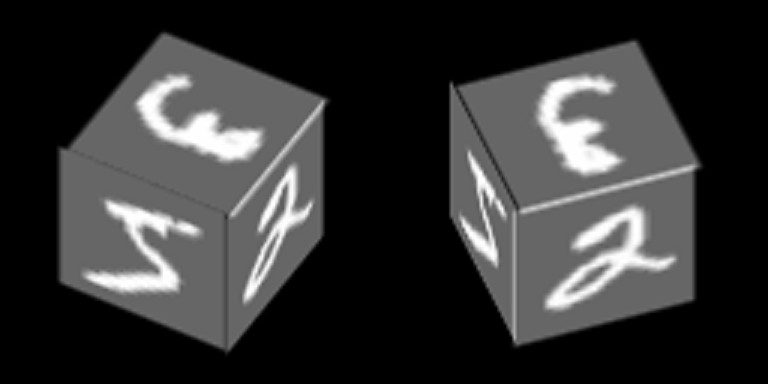
Vamos treinar codificadores automáticos para restaurar faces, orientação de contexto - face.

Aqui está um exemplo do número "zero" em 100 contextos, os primeiros 34 dos quais correspondem a diferentes ângulos de rotação da face lateral e os 76 restantes - ângulos de rotação diferentes da face superior.



Assumimos que para cada uma dessas 100 imagens as “interpretações” devem ser as mesmas e são as combinações aleatórias usadas para o treinamento cruzado.

Após o treinamento com o método descrito acima, foi possível conseguir que o código latente de um dos auto-codificadores possa ser decodificado por outros auto-codificadores, obtendo uma conversão contextual realmente significativa.

Por exemplo, esta imagem mostra como o resultado da codificação do codificador automático no número 10 é decodificado por outros codificadores automáticos para um dos dígitos:



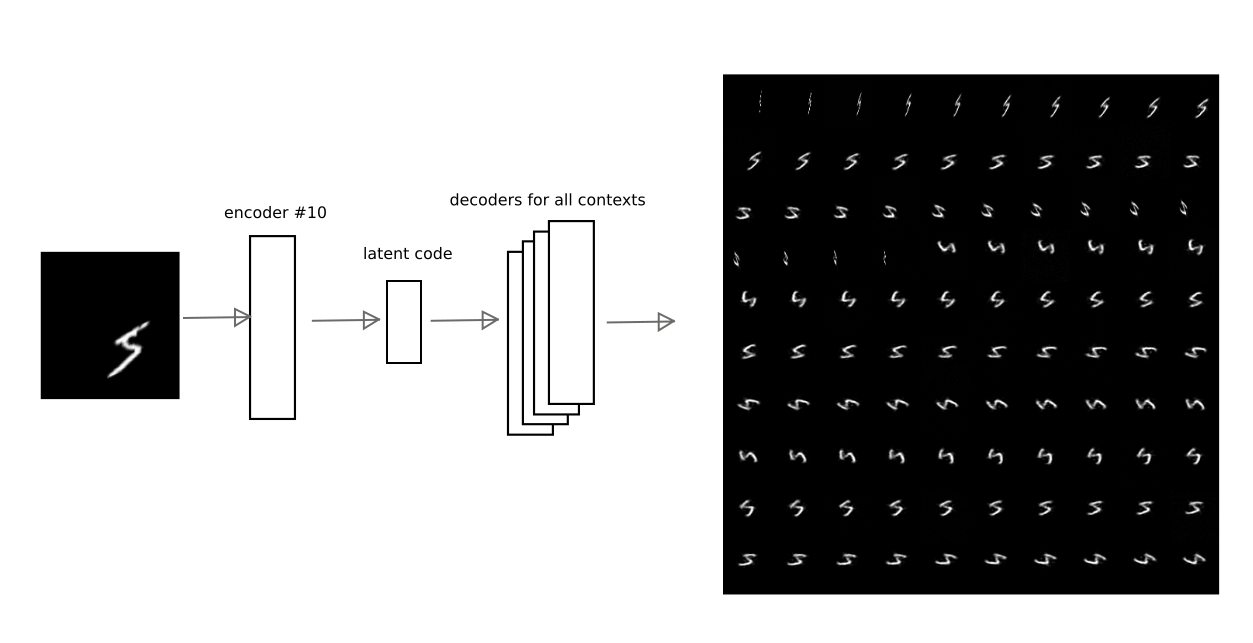
Assim, tendo o código de "interpretação", isto é, vetor latente do codificador automático, você pode restaurar a imagem original em qualquer um dos contextos treinados (ou seja, o decodificador de qualquer codificador automático).

Máscara de vetor de entrada

Na fórmula (4), a dispersão do resíduo $$$\ sigma$ , que é escolhido por uma constante para qualquer um dos componentes do vetor de entrada. No entanto, se alguns componentes não tiverem relação estatística com o modelo latente, a variação provavelmente será significativamente maior para esses componentes. A dispersão está em todo lugar no denominador, o que significa que quanto maior a discrepância, menor a contribuição do erro do componente. Você pode se relacionar com isso como uma máscara de alguma parte do vetor de entrada.

Neste exemplo, com faces rotativas, a máscara é óbvia - a projeção da face em um contexto específico.



Na abordagem simplificada deste exemplo, que usa apenas o resíduo entre a imagem de entrada e a reconstrução, você só precisa multiplicar o resíduo pela máscara para cada um dos contextos.

No caso geral, é necessário avaliar mais rigorosamente os parâmetros de distribuição, sem precisar inserir manualmente a máscara.

Separação da interpretação do contexto

Separando a interpretação do contexto, você pode obter conceitos abstratos. No exemplo treinado, é interessante demonstrar 2 efeitos:

1) aprendizado único, ou seja, treinamento com um número extremamente pequeno de exemplos (no limite de um).

Se analisarmos apenas a interpretação, ignorando o contexto, torna-se possível reconhecer uma nova imagem em diferentes orientações de face, quando uma nova imagem foi mostrada em apenas uma das orientações.

É importante notar que uma nova imagem deve ser apresentada. Por uma questão de correção, também estabelecemos o objetivo de lembrar não uma imagem, mas aprender a compartilhar 2 novas imagens que não foram encontradas anteriormente na base de treinamento do MNIST. Por exemplo, como:



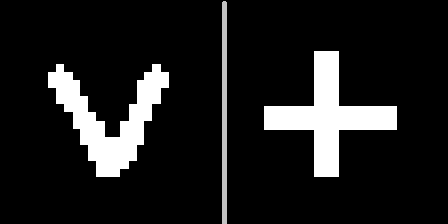A ideia é a seguinte: mostre esses sinais em um dos contextos geométricos (por exemplo, sob o número 10), selecione um hiperplano que seja equidistante das interpretações desses sinais e, em seguida, certifique-se de que, com esse hiperplano, possamos reconhecer que tipo de sinal nos é apresentado quando o rosto é girado (outros contextos).

É importante observar aqui que os codificadores automáticos não serão treinados com novos sinais. Devido à variedade de números que existem no MNIST, é possível prever como um novo personagem que não foi visto antes ficará em diferentes contextos.

Portanto, o sinal V cuidará da codificação no contexto do número 10 e da decodificação nos demais:



pode-se ver que a previsão não é perfeita, mas visualmente reconhecível.

Denotamos essa demonstração como "experimento 1" e descrevemos o resultado abaixo.

2) e com o cubo, é interessante demonstrar o que acontecerá se você ignorar o conteúdo do vetor latente, e apenas o grau de plausibilidade de cada codificador automático é transmitido.

Vamos ver como é a probabilidade de cada um dos contextos para dois cubos com texturas completamente diferentes (números 5 e 9) para 100 contextos que podem ser exibidos como um mapa:



pode-se ver que os mapas são bastante semelhantes, apesar da textura diferente nas laterais do cubo.

I.e.o próprio vetor, contendo a probabilidade de modelos de autoencodificadores (contextos), permite formular um novo conceito abstrato relacionado à forma tridimensional de um cubo. Esse vetor também pode ser descrito no próximo nível por um codificador automático que aprende o modelo do cubo.

No segundo experimento, será necessário criar um segundo nível de processamento de informações para treinar o codificador automático de um modelo de cubo abstrato. E então, usando a projeção traseira para restaurar a imagem original para diferentes implementações do modelo deste cubo. Simplificando, faça o cubo girar.

O resultado do "experimento número 1"

O conjunto de codificadores automáticos treinados pelo MNIST se aplica a duas novas imagens apresentadas no contexto nº 10. Acontece 2 pontos no espaço latente correspondentes aos sinais de V e +. Definimos um plano equidistante de ambos os pontos, que usaremos para tomar uma decisão. Se o ponto estiver em um lado do avião - o sinal V, por outro - o sinal de mais.

Agora, obtemos os códigos das imagens convertidas e, para cada uma delas, calculamos a distância do avião, preservando o sinal.

Como resultado, é possível distinguir que tipo de sinal foi apresentado para todos os 100 contextos.

Distribuição da distância no gráfico:



visualização do resultado usando símbolos individuais como exemplo:



I.e.códigos latentes de sinais V em contextos completamente diferentes estão muito mais próximos no espaço latente que códigos V e sinais de adição no mesmo contexto. Por esse motivo, em 100 dos 100 casos, é possível distinguir com sucesso sinais em várias orientações das faces do cubo, apesar de apenas uma amostra de cada sinal ter sido apresentada.

Foi possível demonstrar o clássico "one-shot learning", que é impossível na arquitetura original das redes neurais artificiais. O princípio básico pelo qual essa abordagem funciona é muito semelhante ao "aprendizado por transferência" demonstrado, por exemplo, neste artigo .

Link para git (train_ae_shared.py, test_AB.py)

O resultado do "experimento número 2"

Separar interpretações do contexto também permite aprender com um conjunto limitado de exemplos. É possível demonstrar apenas uma das possíveis interpretações em vários contextos (fixando um "vetor latente"). Um modelo de cubo abstrato pode ser obtido apenas mostrando um dígito em todas as faces.

O experimento está estruturado da seguinte forma:

1. Está sendo preparada uma base de treinamento: cubos com um grau de rotação de 0 a 90 graus. Nas faces dos cubos está o número 5.
2. O vetor de probabilidade dos contextos, separado da interpretação (código latente), é passado para o próximo nível, onde o codificador automático responsável pelo modelo de cubo é treinado
3. : , «», , , , , .

A amostra de treinamento consistiu em 5421 imagens com a imagem do número 5 nas laterais, por exemplo:


cubos com rotação de 0 a 90 graus

Sabemos antecipadamente que o cubo tem apenas um grau de liberdade de rotação; portanto, o codificador automático no segundo nível tem apenas um componente no código latente. Após o treinamento, você pode variar esse componente de 0 a 1 (a função sigmóide foi selecionada para ativar a camada latente) e ver qual vetor de probabilidade de contexto é reproduzido durante a decodificação:



esse vetor é transferido para o nível 1, no qual 100 contextos de orientação das faces, máximos locais e « imaginado ”qualquer código latente do sinal nas faces do cubo. “Imagine” o número 3 nas faces, alterando o vetor latente no codificador automático responsável pelo conceito abstrato de um cubo e obtenha a seguinte imagem de um cubo:



Ou o código do sinal V, que não foi encontrado no conjunto de treinamento:



a qualidade é pior, mas o sinal é reconhecível.

Assim, no segundo nível de processamento de imagem, obtivemos um codificador automático que modela a variedade do conceito abstrato de “cubo”. Na prática, em problemas de reconhecimento, o princípio de retroprojeção mostrado no experimento é extremamente importante, porque permite eliminar as ambiguidades da interpretação devido à formação de conceitos abstratos de nível superior.

Link para o git (second_level.py, second_level_test.py)

Outros exemplos em que a separação de contexto funciona

No meu artigo anterior, ao reconhecer os números dos carros, um método semelhante foi usado sem explicação. A posição, orientação e escala dos números na imagem foram separadas do conteúdo; o próximo nível percebeu esses dados para construir o modelo de “número do carro”. Independentemente de quais números, sua configuração geométrica mútua é importante, para que possamos dizer com segurança que este é um número de carro (a propósito, também um conceito abstrato).

Por analogia, podemos dar vários outros exemplos da visão computacional: a forma 3D de um objeto ou seus contornos são separáveis ​​de sua textura e fundo; a enumeração dos componentes isoladamente da configuração espacial mútua também freqüentemente permite a formação de um novo conceito abstrato.

, : — ( ) ( ); ( , ,«- -»).

No momento, é difícil formular como a IA forte difere da fraca. Provavelmente, essa lista deve incluir tudo o que está faltando nas abordagens e algoritmos existentes para que os computadores funcionem com a mesma eficiência que uma pessoa, por exemplo:

• Tomar decisões, usar estratégias, resolver em face da incerteza. É alta incerteza que requer a escolha do melhor modelo formulado durante o treinamento
• Reflexão de modelos do mundo físico e social circundante, incluindo autoconsciência e consciência alheia
• Os mecanismos do pensamento abstrato, permitindo formular conceitos que podem ser usados ​​em uma ampla variedade de dados de entrada posteriormente
• Capacidade de "decifrar" seus próprios pensamentos

Além disso, claramente não há mecanismos de memória desenvolvidos suficientes integrados ao processo de aprendizagem, mecanismos de promoção / punição.

O artigo demonstra a abordagem do problema de reconhecimento e estimativa de parâmetros, que se baseia na seleção do melhor modelo que descreve os dados de entrada. Supõe-se que este seja o mecanismo para escolher a melhor interpretação e contexto. Devido à separação da interpretação e do contexto na saída do módulo (um conjunto de auto-codificadores), pode-se formular conceitos abstratos ou generalizar a experiência isoladamente do contexto, reduzindo assim a amostra de treinamento. Conjuntos de contextos podem refletir as leituras dos sensores da máquina (orientação, posição, velocidade etc.), devido às quais o aprendizado natural sem um professor se torna possível.

Além disso, embora o aprendizado profundo seja usado no treinamento de auto-codificadores, os processos que ocorrem nos auto-codificadores são facilmente analisados ​​em cada nível de processamento de informações, porque é possível determinar em qual modelo (ou em que contexto) a melhor interpretação foi encontrada. E o significado dos feedbacks entre os níveis que precisam ser introduzidos em sistemas complexos é aumentar ou diminuir a probabilidade de escolher um contexto específico.

Resultado

É proposto um aparato matemático, com base no qual se pode escolher um ou outro modelo que descreva os dados de entrada, guiados pela regra de decisão bayesiana. Os modelos são obtidos usando auto-codificadores com um espaço latente comum. Uma ideia é proposta segundo a qual o código latente do codificador automático é uma interpretação e o modelo latente, isto é, o próprio codificador automático é o contexto.

É demonstrado que o conjunto de auto-codificadores não é inferior em precisão às redes neurais artificiais totalmente conectadas usando o exemplo de MNIST.

O efeito de separar a interpretação do contexto é mostrado: minimização do conjunto de dados necessário (no limite de “aprendizado único”) para reconhecimento de imagens recém-apresentadas devido ao pré-treinamento em outros dados.

O efeito de separar o contexto da interpretação é mostrado: a possibilidade de formar conceitos abstratos do próximo nível usando o cubo de abstração geométrica como exemplo.

Referências

1) Alain, G. e Bengio, Y. O que os auto-codificadores regularizados aprendem com a distribuição geradora de dados. 2013.
2) Kamyshanska, H. 2013. Na pontuação do autoencoder
3) Daniel Jiwoong Im, Mohamed Ishmael Belghazi e Roland Memisevic. 2016. Conservação de codificadores automáticos desatados
4) Uma arquitetura de rede neural artificial baseada em transformações de contexto em minicolunas corticais. Vasily Morzhakov, Alexey Redozubov
5) Memória holográfica: um novo modelo de processamento de informações por microcircuitos neurais. Alexey Springer Redozubov
6) Não são redes neurais. Morzhakov V.
7) en.wikipedia.org/wiki/Gaussian_integral
8) Exemplos Adversários: Ataques e Defesas para Aprendizado Profundo
9) Aprendizado de imitação de uma só vez

PS: este artigo é uma pré-impressão eletrônica em idioma russo, publicada para discutir os resultados, procurar erros. Qualquer crítica construtiva é bem-vinda!