
As propriedades dos números primos raramente permitem trabalhar com eles de forma diferente da forma de uma matriz pré-calculada - e de preferência o mais volumosa possível. O formato de armazenamento natural na forma de números inteiros com capacidade de um ou outro dígito sofre ao mesmo tempo algumas desvantagens que se tornam significativas com o crescimento do volume de dados.
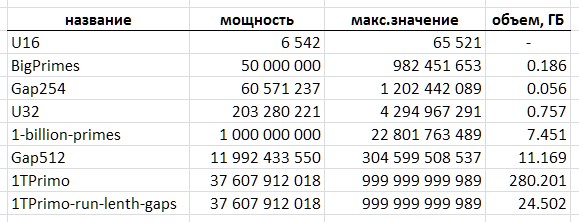
Portanto, o formato de números inteiros não assinados de 16 bits com o tamanho de uma tabela é de cerca de 13 kilobytes, contém apenas 6542 primos: seguidos pelo número 65531 são os valores de profundidade de bits mais alta. Tal mesa é adequada apenas como um brinquedo.
O formato inteiro de 32 bits mais popular na programação parece muito mais sólido - permite armazenar cerca de 203 milhões de formatos simples. Mas essa tabela já ocupa cerca de 775 megabytes.
O formato de 64 bits tem ainda mais perspectivas. No entanto, com um poder teórico da ordem de 1e + 19 valores, a tabela teria um tamanho de 64 exabytes.
Não se acredita realmente que nossa humanidade progressiva jamais calcule, no futuro previsível, uma tabela de números primos desse volume. E o ponto aqui não é tanto em volumes, mas também no tempo de contagem dos algoritmos disponíveis. Digamos, se a tabela de todas as simples de 32 bits ainda puder ser calculada independentemente em algumas horas (Fig. 1), então, para a tabela, pelo menos uma ordem de magnitude maior, levará vários dias. Mas esses volumes hoje - este é apenas o nível inicial.
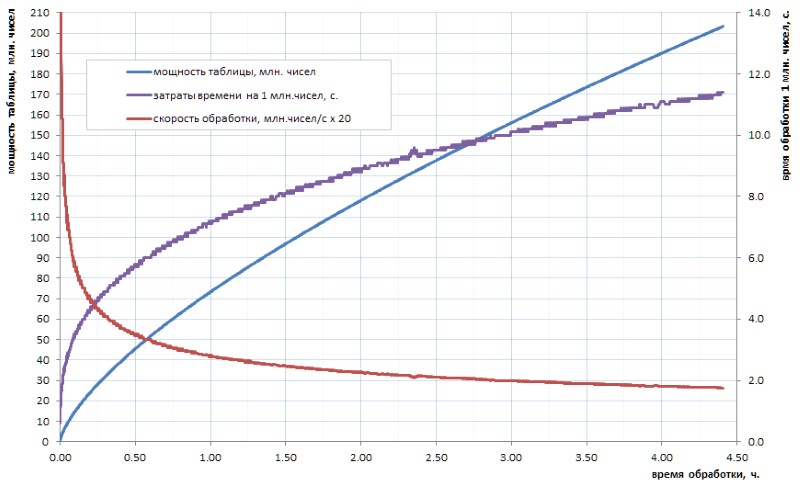
Como pode ser visto no diagrama, o tempo de cálculo específico após o empurrão inicial passa suavemente para o crescimento assintótico. Ele é bastante lento. mas isso é crescimento, o que significa que a mineração de todos os dados ao longo do tempo será cada vez mais difícil. Se você quiser fazer alguma inovação significativa, terá que paralelizar o trabalho entre os núcleos (e ele se assemelha bem) e pendurá-lo nos supercomputadores. Com a perspectiva de simplificar os primeiros 10 bilhões em uma semana e 100 bilhões - apenas em um ano. Certamente, existem algoritmos mais rápidos para calcular simples do que o fracasso trivial usado em minha lição de casa, mas, em essência, isso não muda a questão: depois de duas ou três ordens de magnitude, a situação se torna semelhante.
Portanto, seria bom uma vez ter realizado o trabalho de contagem, armazenar o resultado em uma forma de tabela pronta e usá-lo conforme necessário.
Devido à obviedade da ideia, a rede encontra muitos links para listas prontas de números primos já calculadas por alguém. Infelizmente, na maioria dos casos, eles são adequados apenas para artesanato de estudantes: um deles, por exemplo, vagueia de um local para outro e inclui 50 milhões de trabalhos simples. Esse valor só pode surpreender os não iniciados: já foi mencionado acima que em um computador doméstico em poucas horas você pode calcular independentemente a tabela de todos os simples de 32 bits e é quatro vezes maior. Provavelmente cerca de 15 a 20 anos atrás, essa lista foi de fato uma conquista heróica para a comunidade leiga. Hoje, na era dos dispositivos com vários núcleos, multi-gigahertz e multi-gigabytes, isso não é mais impressionante.
Tive a sorte de me familiarizar com o acesso a uma tabela muito mais representativa de tabelas simples, que usarei mais como ilustração e sacrifício para minhas experiências de campo. Para fins de conspiração, vou chamá-la de 1TPrimo . Ele contém todos os números primos menores que um trilhão.
Usando o 1TPrimo como exemplo, é fácil ver com quais volumes você precisa lidar. Com uma capacidade de cerca de 37,6 bilhões de valores no formato inteiro de 64 bits, esta lista tem 280 gigabytes. A propósito - a parte que pode caber em 32 dígitos representa apenas 0,5% do número de números representados nela. Isso deixa absolutamente claro que qualquer trabalho sério com números primos inevitavelmente tende a totalizar profundidades de 64 bits (ou mais).
Assim, a tendência sombria é óbvia: uma tabela de números primos, de alguma forma séria, inevitavelmente tem um volume titânico. E devemos de alguma forma combater isso.
A primeira coisa que vem à mente quando se olha para uma tabela (Fig. 2) é que ela consiste em valores consecutivos quase idênticos que diferem apenas em uma ou duas das últimas casas decimais:
Simplesmente, das considerações abstratas mais gerais: se o arquivo tiver muitos dados duplicados, ele deverá ser compactado pelo arquivador. De fato, a compactação da tabela 1TPrimo com o popular utilitário 7-zip nas configurações padrão deu uma taxa de compactação bastante alta: 8,5. É verdade que o tempo de processamento - com o tamanho enorme da tabela de origem - em um servidor de 8 núcleos, com uma carga média de todos os núcleos de 80 a 90%, foi de 14 horas e 12 minutos. Os algoritmos de compressão universal são projetados para algumas idéias abstratas e generalizadas sobre dados. Em alguns casos especiais, algoritmos de compactação especializados criados com os recursos conhecidos do conjunto de dados recebidos podem demonstrar indicadores muito mais eficazes, aos quais esse trabalho é dedicado. E quão eficaz será claro abaixo.
Os valores numéricos próximos dos números primos vizinhos pedem uma decisão de não armazenar esses valores eles mesmos, mas os intervalos (diferenças) entre eles. Nesse caso, economias significativas podem ser obtidas devido ao fato de a profundidade de bits dos intervalos ser muito menor que a profundidade de bits dos dados iniciais (Fig. 3).
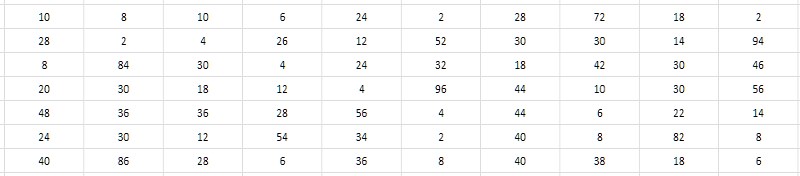
E parece que isso não depende da profundidade de bits dos simples que geram o intervalo. Uma pesquisa exaustiva mostra que os valores típicos de intervalos para números primos obtidos de vários lugares na tabela 1TPrimo estão dentro de unidades, dezenas, às vezes centenas, e - como a primeira sentença de trabalho - eles provavelmente poderiam caber no intervalo de 8 bits números inteiros não assinados, ou seja, bytes. Seria muito conveniente e, em comparação com o formato de 64 bits, isso imediatamente levaria a uma compressão de dados de 8 vezes - apenas em algum lugar no nível demonstrado pelo arquivador de 7 zip. Além disso, a simplicidade dos algoritmos de compactação e descompactação deve, em princípio, ter um grande impacto na velocidade da compactação e do acesso aos dados em comparação com o 7-zip. Parece tentador.
É absolutamente claro que os dados convertidos de seus valores absolutos para os intervalos relativos entre eles são adequados apenas para restaurar uma série de valores que seguem uma linha desde o início da tabela principal. Mas se adicionarmos uma estrutura mínima de índice de bloco a essa tabela de intervalos, então, com custos indiretos adicionais insignificantes, isso nos permitirá restaurar - mas já bloquear por bloco - o elemento da tabela por seu número e o elemento mais próximo por um valor definido arbitrariamente, e essas operações, juntamente com a operação principal amostras de sequência - em geral, esgota a maior parte das consultas possíveis para esses dados. O processamento estatístico, é claro, se tornará mais complicado, mas continuará sendo bastante transparente, como não há truque específico para recuperá-lo "em tempo real" dos intervalos disponíveis ao acessar o bloco de dados necessário.
Mas infelizmente. Um experimento numérico simples com dados do 1TPrimo mostra que já no final da terceira dezenas de milhões (isso é menos de um centésimo de um por cento do volume do 1TPrimo) - e depois em qualquer outro lugar - os intervalos entre os primos adjacentes ficam regularmente fora do intervalo de 0..255.
No entanto, um experimento numérico um pouco complicado revela que o crescimento do intervalo máximo entre os primos vizinhos com o crescimento da própria tabela é muito, muito lento - o que significa que a ideia ainda é boa de alguma forma.
O segundo olhar mais atento à tabela de intervalos sugere que é possível armazenar não a diferença em si, mas a metade. Como todos os números primos maiores que 2 são obviamente ímpares, respectivamente, suas diferenças são obviamente pares. Consequentemente, as diferenças podem ser reduzidas em 2 sem perda de valor; e para completar, pode-se também subtrair um do quociente obtido, a fim de usar utilmente o valor zero que não foi reivindicado de outra forma (Fig. 4). Essa redução de intervalos será denominada a seguir monolítica, em contraste com a forma inicial frouxa e porosa, na qual todos os valores ímpares e zero acabaram não sendo reclamados.
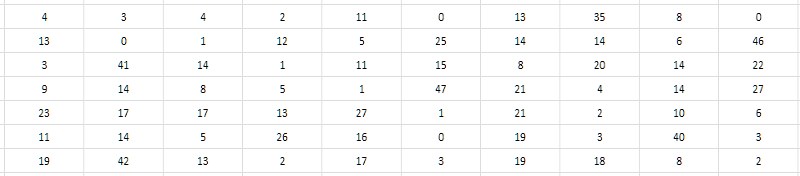
Deve-se notar que, como o intervalo entre os dois primeiros simples (2 e 3) não se enquadra nesse esquema, 2 deverá ser excluído da tabela de intervalos e manter esse fato em mente o tempo todo.
Essa técnica simples permite codificar intervalos de 2 a 512 no intervalo de valores de 0 a 255. Mais uma vez, surge a esperança de que o método da diferença nos permita agrupar uma sequência de primos muito mais poderosa. E com razão: uma série de 37,6 bilhões de valores apresentados na lista 1TPrimo revelou apenas 6 (seis!) Intervalos que não estão na faixa 2..512.
Mas essas foram boas notícias; o ruim é que esses seis intervalos estão espalhados pela lista bastante livremente, e o primeiro deles já ocorre no final do primeiro terço da lista, transformando os dois terços restantes em lastro inadequados para esse método de compressão (Fig. 5):
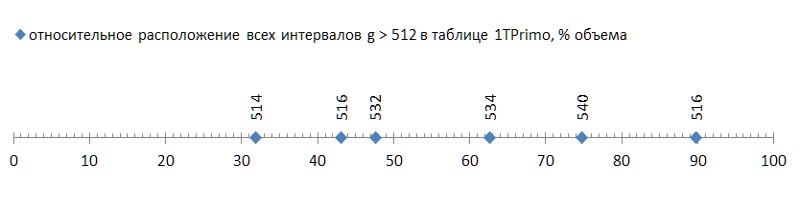
Tal descarga (algumas infelizes seis peças por quase quarenta bilhões! - e para você ...) mesmo com uma mosca na pomada para comparar - para mostrar a honra do alcatrão. Mas, infelizmente, este é um padrão, não um acidente. Se traçarmos a primeira aparência de intervalos entre primos, dependendo do tamanho dos dados, fica claro que esse fenômeno reside na genética dos primos, embora progrida extremamente lentamente (Fig. 6 *).
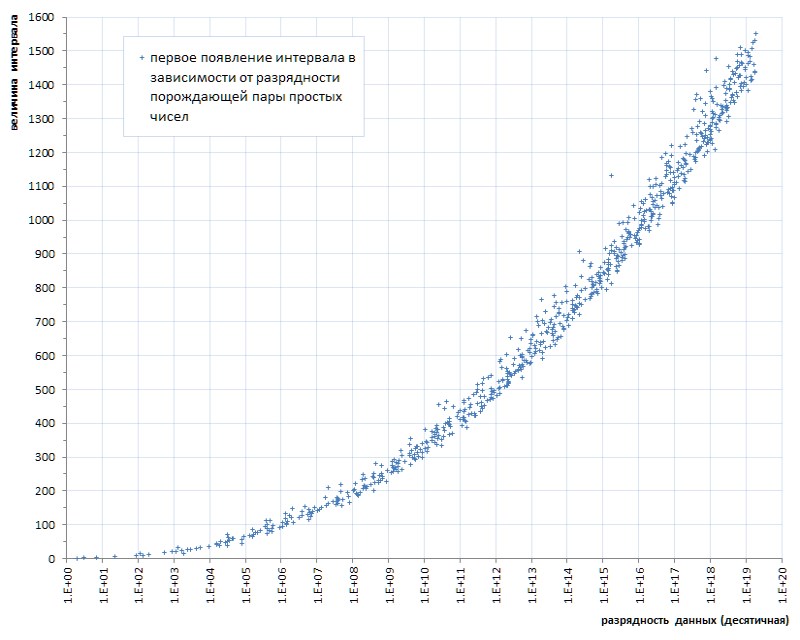
* Programação compilada de acordo com o site temático de Thomas R. Nisley ,
que são várias ordens de magnitude superiores ao poder da lista 1TPrimo
Mas mesmo esse progresso muito lento indica sem ambiguidade: é possível limitar-se a uma certa profundidade de intervalo de bits predeterminada apenas a um certo poder predeterminado da lista. Ou seja, não é adequado como solução universal.
No entanto, o fato de o método proposto de compactação de uma sequência de números primos permitir a implementação de uma tabela compacta simples com uma capacidade de quase 12 bilhões de valores já é um resultado. Essa tabela ocupa um volume de 11,1 gigabytes - contra 89,4 gigabytes em um formato trivial de 64 bits. Certamente, para várias aplicações, essa solução pode ser suficiente.
E o que é interessante: o procedimento para converter uma tabela 1TPrimo de 64 bits para o formato de intervalos de 8 bits com uma estrutura de bloco, usando apenas um núcleo do processador (para paralelização, você teria que recorrer a uma complicação significativa do programa, e não valia a pena) e não mais do que 5 % da carga do processador (na maioria das vezes gasta em operações de arquivo) levou apenas 19 minutos. Contra, lembro-me, 14 horas em oito núcleos, com 80-90% da carga gasta pelo arquivador de 7 zip.
Obviamente, apenas o primeiro terço da tabela foi submetido a essa tradução, na qual o intervalo de intervalos não excede 512. Portanto, se levarmos as 14 horas completas para o mesmo terço, 19 minutos devem ser comparados com quase 5 horas do arquivador de 7 zip. Com uma quantidade comparável de compactação (8 e 8,5), a diferença é de cerca de 15 vezes. Considerando que a maior parte do tempo de trabalho do programa de transmissão era ocupada por operações de arquivos, a diferença seria ainda mais acentuada em um sistema de disco mais rápido. E intelectualmente, o tempo de operação do 7-zip em oito núcleos ainda deve ser contado em um thread e, em seguida, a comparação se tornará realmente adequada.
A seleção desse banco de dados difere muito pouco da seleção da tabela de dados descompactados e é quase inteiramente determinada pelo tempo das operações do arquivo. Os números específicos dependem fortemente do hardware específico; no meu servidor, em média, o acesso a um bloco de dados arbitrário levou 37,8 μs, enquanto a leitura sequencial de blocos - 4,2 μs por bloco, para a descompactação completa do bloco - menos de 1 μs. Ou seja, não faz sentido comparar a descompressão de dados com o trabalho de um arquivador padrão. E esta é uma grande vantagem.
E, finalmente, as observações oferecem mais uma terceira solução que remove quaisquer restrições ao poder dos dados: intervalos de codificação com valores de comprimento variável. Essa técnica tem sido amplamente utilizada em aplicativos relacionados à compactação. Seu significado é que, se for encontrado na entrada que alguns valores são frequentemente encontrados, alguns são menos comuns e alguns são muito raros, então podemos codificar o primeiro com códigos curtos, o segundo com códigos mais autênticos e o terceiro - muito longo (talvez até muito longo, porque não importa: mesmo assim, esses dados são muito raros). Como resultado, o comprimento total dos códigos recebidos pode ser muito menor que os dados de entrada.
Já observando o gráfico da aparência dos intervalos na Fig. 7, podemos supor que, se os intervalos forem 2, 4, 6, etc. aparecer antes dos intervalos, digamos, 100, 102, 104 etc., o primeiro deve continuar ocorrendo com muito mais frequência do que o segundo. E vice-versa - se os intervalos 514 aparecerem apenas a partir de 11,99 bilhões, 516 - a partir de 16,2 bilhões e 518 - geralmente a partir de 87,7 bilhões, então eles serão muito raros. Ou seja, a priori, podemos assumir a relação inversa entre o tamanho do intervalo e sua frequência em uma sequência de números primos. E isso significa - você pode construir uma estrutura simples que implemente códigos de comprimento variável para eles.
Obviamente, as estatísticas sobre a frequência dos intervalos devem se tornar determinantes para a escolha de um método de codificação específico. Felizmente, em contraste com os dados arbitrários, a frequência dos intervalos entre os primos - que por si só são uma sequência estritamente determinada, de uma vez por todas - é também uma característica estritamente determinada, de uma vez por todas definida.
A Figura 7 mostra a resposta em frequência dos intervalos para toda a lista 1TPrimo:
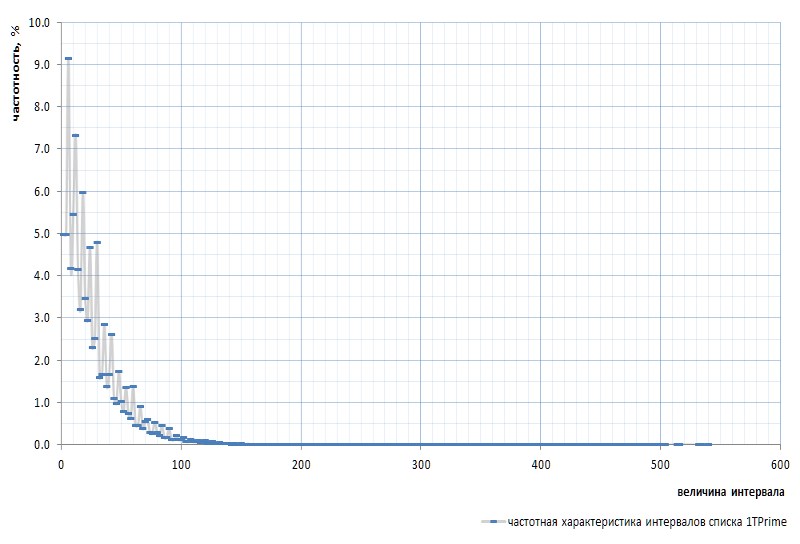
Aqui é necessário mencionar novamente que o intervalo entre os primeiros primos 2 e 3 é excluído do gráfico: esse intervalo é 1 e ocorre exatamente uma vez na sequência de primos, independentemente do poder da lista. Esse intervalo é tão peculiar que é mais fácil remover 2 da lista de simples do que se afastar constantemente das reservas. O sim é declarado que o número 2 é virtual prime : não é visível nas listas, mas está lá. Como aquele esquilo.
À primeira vista, o gráfico de frequência confirma completamente a suposição a priori dada por alguns parágrafos acima. Mostra claramente a heterogeneidade estatística dos intervalos e a alta frequência de valores pequenos em comparação com os grandes. No entanto, na segunda visão mais convexa, o gráfico acaba sendo muito mais interessante (Fig. 8):
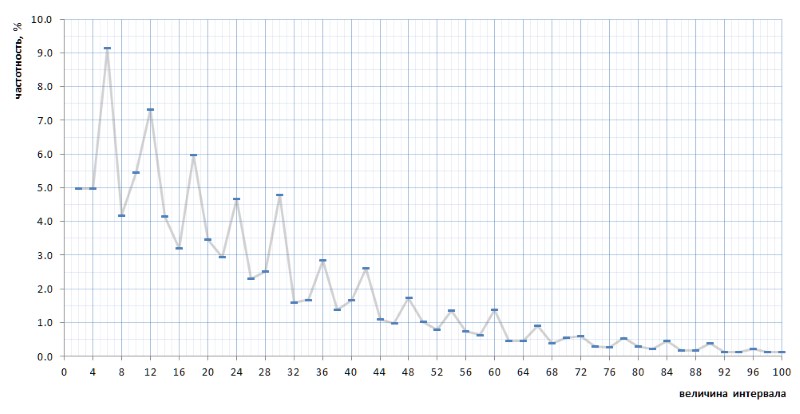
Inesperadamente, verifica-se que os intervalos mais freqüentes não são 2 e 4, como parecia ser de considerações gerais, mas 6, 12 e 18, seguidos por 10 - e somente então 2 e 4 com frequência quase igual (diferença em 7 dígitos após o ponto decimal). Além disso, a multiplicidade de valores de pico do número 6 é rastreada em todo o gráfico.
Ainda mais interessante, essa natureza inadvertidamente revelada do gráfico é universal - e, com todos os detalhes, com todas as suas torções - durante toda a sequência de intervalos simples representados pela lista 1TPrimo, é provável que seja universal para qualquer sequência de intervalos simples (é claro, uma afirmação tão ousada precisa de provas, que com grande prazer transfiro para os ombros dos especialistas em teoria dos números). A Figura 10 mostra uma comparação das estatísticas do intervalo completo (linha escarlate) com amostras de intervalo limitadas coletadas em vários locais arbitrários na lista 1TPrimo (linhas de outras cores):
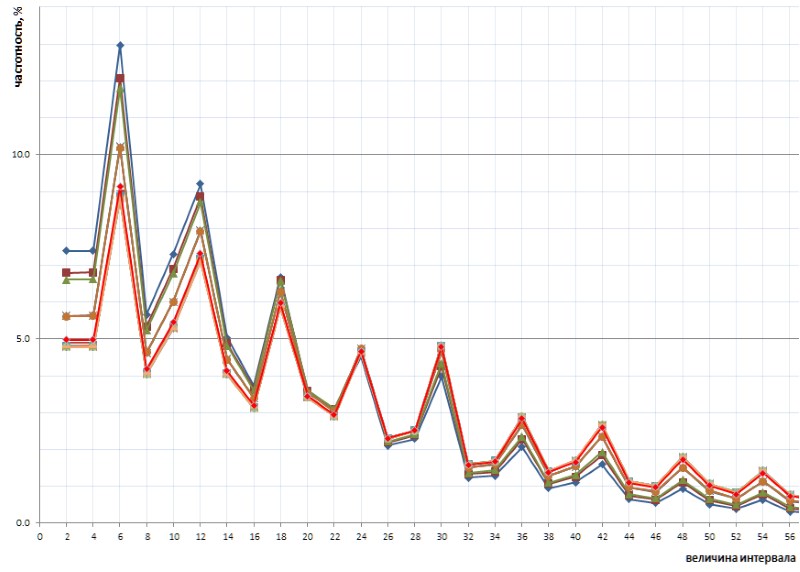
Pode-se ver neste gráfico que todas essas amostras se repetem exatamente, com apenas uma pequena diferença nas partes esquerda e direita da figura: elas parecem ser levemente giradas no sentido anti-horário em torno do ponto de intervalo com um valor de 24. Essa rotação é provavelmente devida ao fato de que quanto maior a esquerda partes dos gráficos são construídas em amostras com profundidades de bits mais baixas. Nessas amostras, ainda não existem, ou grandes intervalos são raros, que se tornam frequentes em amostras com profundidades de bits mais altas. Consequentemente, sua ausência é a favor da frequência de intervalos com valores mais baixos. Em amostras com profundidades de bits mais altas, muitos novos intervalos com grandes valores aparecem; portanto, a frequência de intervalos menores diminui ligeiramente. Muito provavelmente, o ponto de pivô, com um aumento no poder da lista, mudará para valores maiores. Em algum lugar, próximo a ele, está o ponto de equilíbrio do gráfico, onde a soma de todos os valores à direita é aproximadamente igual à soma de todos os valores à esquerda.
Essa natureza interessante da frequência dos intervalos sugere abandonar a estrutura trivial dos códigos de comprimento variável. Normalmente, essa estrutura consiste em um pacote de bits de vários comprimentos e finalidades. Por exemplo, primeiro vem um certo número de bits de prefixo definido para um valor específico, por exemplo, 0. Há um bit de parada atrás deles, que deve indicar a conclusão do prefixo e, portanto, deve diferir do prefixo: 1 nesse caso. O prefixo pode não ter nenhum comprimento, ou seja, repetidamente, a amostragem pode começar imediatamente com um bit de parada, determinando assim a menor seqüência. O bit de parada é geralmente seguido por um sufixo, cujo comprimento é determinado de alguma maneira predeterminada pelo comprimento do prefixo. , , — . , - . - (, , - ) , .
, .
E aqui mais uma coisa importante deve ser declarada. À primeira vista, a ciclicidade observada implica a divisão dos intervalos em triplos: {2,4, 6 } , {8,10, 12 } , {14,16, 18 } e assim por diante (os valores com a frequência máxima em cada tripla são marcados em negrito) . No entanto, de fato, o ciclo aqui é um pouco diferente.
Não citarei toda a linha de raciocínio, que, de fato, não existe: foi um palpite intuitivo, complementado por um método de enumeração abrupta de opções, cálculos e amostras que levou vários dias intermitentemente. A ciclicidade revelada como resultado consiste em seis intervalos {2,4, 6 ,8,10, 12 } , {14,16, 18 ,20,22, 24 } , {26,28, 30 ,32,34, 36 } e assim por diante (os intervalos de frequência máxima são novamente destacados em negrito).
Em poucas palavras, o algoritmo de empacotamento proposto é o seguinte.
Dividir os intervalos em seis de números pares nos permite representar qualquer intervalo g na forma g = i * 12 + t , onde i é o índice dos seis aos quais esse intervalo pertence ( i = {0,1,2,3, ...} ) e t é uma cauda que representa um dos valores de uma rigidamente definida, delimitada e idêntica para qualquer seis do conjunto {2,4,6,8,10,12} . A resposta em frequência do índice destacado acima é quase exatamente inversamente proporcional ao seu valor, portanto, é lógico converter o índice seis em uma estrutura trivial de um código de tamanho variável, um exemplo do que é dado acima. As características de frequência do pinça permitem dividi-lo em dois grupos que podem ser codificados com cadeias de bits de diferentes comprimentos: os valores 6 e 12, que são mais frequentemente encontrados, são codificados com um bit, os valores 2, 4, 8 e 10, encontrados com muito menos frequência, são codificados com dois bits. Obviamente, é necessário mais um bit para distinguir entre essas duas opções.
Uma matriz contendo pacotes de bits é complementada por campos fixos que especificam os valores iniciais dos dados apresentados no bloco e outras quantidades necessárias para restaurar uma sequência ou simples arbitrária de valores simples a partir dos intervalos armazenados no bloco.
Além dessa estrutura de índice de bloco, o uso de códigos de comprimento variável é complicado pelos custos adicionais em comparação com intervalos de bits fixos.
Ao usar intervalos de tamanho fixo, determinar o bloco no qual procurar um número primo por seu número de série é uma tarefa bastante simples, porque o número de intervalos por bloco é conhecido antecipadamente. Mas a busca de uma solução simples para o valor mais próximo não tem uma solução direta. Como alternativa, você pode usar alguma fórmula empírica que permita encontrar o número aproximado do bloco com o intervalo necessário, após o qual será necessário procurar o bloco desejado por meio de uma pesquisa exaustiva.
Para uma tabela com códigos de comprimento variável, a mesma abordagem é necessária para as duas tarefas: tanto para buscar um valor por número quanto para procurar por valor. Como o comprimento dos códigos varia, nunca se sabe de antemão quantas diferenças estão armazenadas em um bloco específico e em qual bloco o valor desejado está. Foi determinado experimentalmente que, com um tamanho de bloco de 512 bytes (que inclui alguns bytes de cabeçalho), a capacidade do bloco pode subir de 10 a 12% do valor médio. Blocos menores dão uma dispersão relativa ainda maior. Ao mesmo tempo, o valor médio da capacidade do bloco tende a diminuir lentamente à medida que a tabela cresce. A seleção de fórmulas empíricas para determinação imprecisa do bloco inicial para procurar o valor desejado, tanto por número quanto por valor, é uma tarefa não trivial. Como alternativa, você pode usar a indexação mais complexa e sofisticada.
Isso, de fato, é tudo.
Abaixo, as sutilezas de compressão de uma tabela primária usando códigos de comprimento variável e as estruturas associadas a ela são descritas de maneira mais formal e detalhada, e é fornecido o código para as funções de intervalo de empacotamento e descompactação em C.
O resultado.
A quantidade de dados convertidos da Tabela 1TPrimo em códigos de comprimento variável, complementados por uma estrutura de índice de bloco, também descrita abaixo, totalizou 26.309.295.104 bytes (24,5 GB), ou seja, a taxa de compactação atinge 11,4. Obviamente, com o aumento da profundidade de bits, a taxa de compressão aumentará.
O tempo de transmissão de 280 GB da tabela 1TPrimo no novo formato foi de 1 hora. Este é o resultado esperado após experimentos com intervalos de compactação em números inteiros de byte. Nos dois casos, a conversão da tabela de origem consiste principalmente em operações de arquivo e quase não carrega o processador (no segundo caso, a carga ainda é maior devido à maior complexidade computacional do algoritmo). O tempo de acesso aos dados também não é muito diferente dos intervalos de byte único, mas o tempo para descompactar um bloco completo do mesmo tamanho levou 1,5 μs, devido à maior complexidade do algoritmo para extrair códigos de tamanho variável.
A tabela (Fig. 10) resume as características volumétricas das tabelas de números primos mencionadas neste texto.
Descrição do algoritmo de compressão
Termos e Notação
P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 são números primos de acordo com seus números de série. Mais uma vez (e pela última vez) enfatizo que
P0=2 é um número primo virtual; por uma questão de uniformidade formal, esse número é fisicamente excluído da lista de números primos.
G (gap) - o intervalo entre dois primos consecutivos Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...} .
D (dense) - reduzido a um intervalo de forma monolítica: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} . Os seis intervalos na forma monolítica se parecem com {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} etc.
Q (quotient) - índice dos seis reduzido para uma forma monolítica, Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}
R (remainder) - o restante dos seis monolíticos R = D mod 6. R sempre tem um valor no intervalo {0,1,2,3,4,5} .
Os valores Q e R obtidos pelo método acima a partir de qualquer intervalo arbitrário G , devido às suas características de frequência estáveis, estão sujeitos a compressão e armazenamento na forma de pacotes de bits de comprimento variável, descritos abaixo. As cadeias de bits que codificam os valores Q e R em um pacote são criadas de diferentes maneiras: para codificar o índice Q , a cadeia de bits do prefixo H , fluxo F e o bit auxiliar S , e o grupo de bits do infixo X e do bit auxiliar A é usado para codificar o restante R
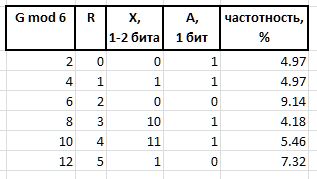
A (arbiter) - um bit que determina o tamanho do infixo X : 0 - infixo de um bit, 1 - dois bits.
X (infix) - X (infix) 1 ou 2 bits, juntamente com o bit árbitro R forma tabular (a tabela também mostra a frequência dos seis primeiros com esses infixos para referência):
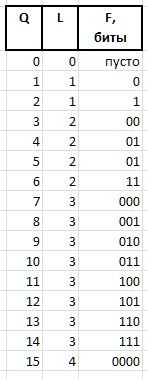
F (fluxion) é uma fluxion, uma derivada do índice Q comprimento variável L={0,1,2...} , projetada para distinguir entre a semântica das strings de bits (), 0, 00, 000, ou 1, 01, 001 , etc. d.
Uma cadeia de bits de unidades de comprimento L é expressa como 2^L - 1 (o sinal ^ significa exponenciação). Na notação C, o mesmo valor pode ser obtido pela expressão 1<<L - 1 . Então o valor da fluxia de comprimento L pode ser obtido de Q expressão
F = Q - (1 << L - 1),
e restaurar Q da fluxia por expressão
Q = (1 << L - 1) + F.
Como exemplo, para as quantidades Q = {0..15} , as seguintes cadeias de bits fluxia serão obtidas:
Os últimos dois campos de bits necessários para compactar / restaurar valores são:
H (header) - prefixo, uma sequência de bits definida como 0.
S (stop) - bit de parada definido como 1, finalizando o prefixo.
De fato, esses bits são processados primeiro em cadeias de bits, permitindo determinar durante a descompactação ou definir durante o empacotamento o tamanho do fluxo e o início dos campos de árbitro e fluxo - imediatamente após o bit de parada.
W (width) - a largura do código inteiro em bits.
A estrutura completa do pacote de bits é mostrada na Fig. 11:
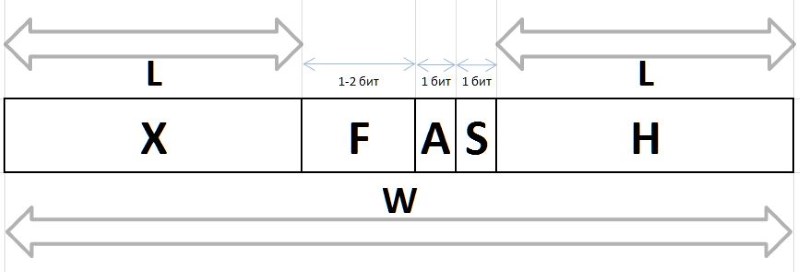
Os valores de Q e R recuperados dessas cadeias nos permitem restaurar o valor inicial do intervalo:
D = Q * 6 + R,
G = (D + 1) * 2,
e a sequência de intervalos restaurados permite restaurar os números primos originais de um determinado valor base do bloco (bloco inicial de intervalos), adicionando a ele todos os intervalos de um determinado bloco sequencialmente.
Para trabalhar com cadeias de bits, é usada uma variável inteira de 32 bits, na qual os bits menos significativos são processados e, após usá-los, os bits são deslocados para a esquerda ao empacotar ou para a direita ao descompactar.
Estrutura de bloco
Além das cadeias de bits, um bloco contém informações necessárias para buscar ou adicionar bits, além de determinar o conteúdo de um bloco.
// // typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // : , #define HEADSIZE (8+8+2+2+2) // , #define BODYSIZE (BLOCKSIZE-HEADSIZE) // . // typedef struct { HUGE base; // , HUGE card; // WORD count; // WORD delta; // base+delta = WORD offset; // BYTE body[BODYSIZE]; // } crunch_block; // , put() get() crunch_block block; // . // NB: len/val rev/rel // , , // . static struct tail_t { BYTE len; // S A BYTE val; // , A - S BYTE rev; // BYTE rel; // } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; // BOOL put(int gap) { // 1. int Q, R, L; // (), (), int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } // L val = Q - (1 << L) + 1; // val <<= tails[R].len; val += tails[R].val; // val <<= L; // L += L + tails[R].len; // // 2. val L buffer put_index if (block.offset + L > BODYSIZE * 8) // ! return FALSE; Q = (block.offset / 8); // , R = block.offset % 8; // block.offset += L; // block.count++; // block.delta += gap; if (R > 0) // { val <<= R; val |= block.body[Q]; L += R; } // L = L / 8 + ((L % 8) > 0 ? 1 : 0); // while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } // int get_index; // // int get() { if (get_index >= BODYSIZE * 8) return 0; // int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; // 4 if (val == 0) return -1; // ! int Q, R, L, F, M, len; // , , , , L = 0; while (!(val & 1)) { val >>= 1; L++; } // - if ((val & 3) == 1) // R = (val >> 2) & 1; // else R = ((val >> 2) & 3) + 2; // len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); // F = val & M; // Q = F + M; // return 2 * (1 + (6 * Q + tails[R].rev)); // }
Aprimoramentos
Se alimentarmos a base de intervalos obtida para o mesmo arquivador de 7 zip, em uma hora e meia de trabalho intensivo em um servidor de 8 núcleos, ele poderá compactar o arquivo de entrada em quase 5%. Ou seja, no banco de dados de intervalos de comprimento variável do ponto de vista do arquivador, ainda existe alguma redundância. Portanto, há motivos para especular um pouco (no bom sentido da palavra) sobre o tópico de reduzir ainda mais a redundância de dados.
O determinismo fundamental da sequência de intervalos entre os números primos torna possível fazer cálculos exatos da eficiência da codificação por um método ou por outro. Em particular, pequenos esboços (e um tanto caóticos) permitiram tirar uma conclusão fundamental sobre as vantagens da codificação de seis sobre triplos e sobre as vantagens do método proposto sobre códigos triviais de comprimento variável (Fig. 12):
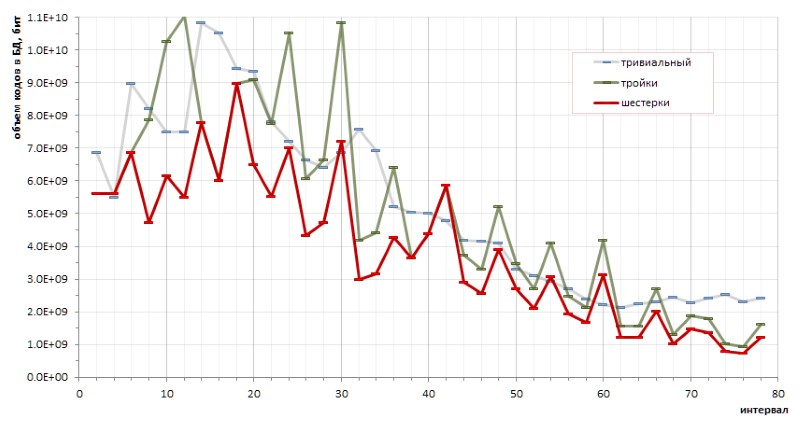
No entanto, os altos irritantes do gráfico vermelho indicam de forma transparente que pode haver outros métodos de codificação que tornariam o gráfico ainda mais suave.
Outra direção sugere verificar a frequência de intervalos consecutivos. De considerações gerais: como os intervalos 6, 12 e 18 são os mais comuns em uma população de números primos, é provável que sejam encontrados com mais frequência em pares (dupletos), triplos (trigêmeos) e combinações semelhantes de intervalos. Se a repetibilidade de dupletos (e talvez até trigêmeos ... bem, de repente!) Acaba sendo estatisticamente significativa na massa total de intervalos, faz sentido traduzi-los em algum código separado.
O experimento em grande escala revela uma certa predominância de dupletos individuais sobre outros. No entanto, se a liderança absoluta for esperada para o par (6,6) - 1,37% de todos os dupletos - os outros vencedores desta classificação serão muito menos óbvios:
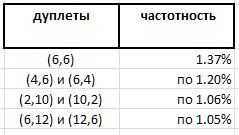
E, como o dupleto (6,6) simétrico, e todos os outros dupletos observados são assimétricos e são encontrados no ranking por duplas espelhadas com a mesma frequência, parece que o registro recorde do dupleto (6,6) nesta série deve ser dividido pela metade entre duplos indistinguíveis (6,6) e (6,6) , o que leva 0,68% até o limite da lista de prêmios. E isso confirma mais uma vez a observação de que nenhuma hipótese verdadeira sobre números primos pode acontecer sem surpresas.
As estatísticas dos trigêmeos também demonstram a liderança de tais triplos intervalos, que não se encaixam perfeitamente na suposição especulativa procedente da maior frequência dos intervalos 6, 12, 18. Em ordem decrescente de popularidade, os líderes de frequência entre os trigêmeos são os seguintes:

etc.
Receio, no entanto, que os resultados de minhas especulações sejam menos interessantes para os programadores do que para os matemáticos, talvez por causa das correções inesperadas feitas pela prática em suposições intuitivas. É improvável que seja possível extrair qualquer dividendo substancial da porcentagem mencionada de frequência em favor de um aumento adicional na taxa de compactação, enquanto a complexidade do algoritmo ameaça crescer muito significativamente.
Limitações
Já foi observado acima que o aumento no valor máximo dos intervalos em conexão com a capacidade dos números primos é muito, muito lento. Em particular, pode ser visto na Fig. 6 que o intervalo entre quaisquer primos que podem ser representados no formato de um número inteiro não assinado de 64 bits será obviamente menor que 1600.
A implementação descrita permite empacotar e descompactar corretamente os valores de intervalo de 18 bits (na verdade, o primeiro erro de empacotamento ocorre com um intervalo de entrada de 442358). Não tenho imaginação suficiente para supor que o banco de dados de intervalos primos possa crescer para esses valores: de improviso, é algo em torno de números inteiros de 100 bits e para calcular com mais precisão a preguiça. Em um caso de incêndio, expandir o intervalo de intervalos às vezes não será difícil.
Obrigado por ler neste lugar :)