Este artigo discute o uso da biblioteca geométrica de funções WebGeometry na construção de modelos de poliedros complexos. A biblioteca está escrita em Javascript.
Um link para o GitHub com um exemplo que fornece um exemplo simples de uso da biblioteca. Comentários e críticas são bem-vindos.
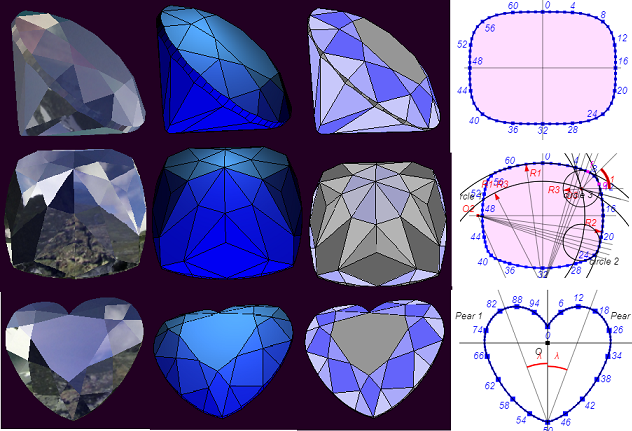
A biblioteca ThreeJS é usada para exibir modelos pré-calculados usando funções da biblioteca WebGeometry. A tela HTML5 é usada para exibir elementos individuais do modelo plano e exibir informações de suporte.
A tecnologia WebGL e as bibliotecas criadas com base nisso, como ThreeJS e BadylonJS, são usadas na Internet para implementar uma variedade de finalidades relacionadas aos gráficos 3D. Mas, basicamente, eles são usados para exibir modelos tridimensionais prontos em um navegador (criado anteriormente, por exemplo, nos programas
3ds Max ou
Blender ). Se formos confrontados com a tarefa de criar um modelo paramétrico, ou seja, um modelo para o qual, no processo de exibição de um objeto finalizado no navegador, podemos alterar seus elementos individuais definindo os parâmetros de modelo apropriados (por exemplo, aumentar o ângulo de uma determinada face), precisamos ter um conjunto de funções geométricas que permitirão criar um modelo para que, no futuro, haja a possibilidade de variar interativamente a forma dos elementos individuais do modelo ou de todo o modelo. Para resolver esse problema, precisamos de um conjunto de funções na linguagem Javascript que implementem os métodos usados na geometria analítica. A biblioteca deve ter funções para criar linhas, planos e círculos, encontrar pontos (ou linhas) de sua interseção, criar planos inclinados e muito mais. As bibliotecas ThreeJS e BadylonJS possuem alguns desses recursos, mas o número de ações executadas com elas não permitirá que você conclua todas as tarefas que surgem ao construir um modelo paramétrico. Existem várias bibliotecas Javascript puramente matemáticas. Destes,
glMatrix e
Sylvester são os mais amplamente utilizados. A biblioteca
glMatrix destina-se principalmente ao trabalho com vetores, matrizes e quaternions, mas não há funções para trabalhar com linhas e planos. A biblioteca
Sylvester tem essas funções, mas elas estão presentes em uma quantidade bastante limitada. No entanto, existem vários livros que descrevem a implementação de métodos de geometria analítica em C / C ++. Os programas C / C ++ correspondentes podem ser usados como protótipos para criar uma biblioteca matemática em Javascript. Portanto, quando decidi criar modelos paramétricos tridimensionais de cortes de diamante para exibi-los em um navegador, a biblioteca ThreeJS foi escolhida por mim apenas para exibir modelos já calculados - não foi usada para calcular a forma dos modelos. Para o cálculo do próprio formulário, foi criada a biblioteca WebGeometry. Essa biblioteca foi baseada nas funções geométricas usadas anteriormente em C / C ++, que eu traduzi para a linguagem Javascript. Vamos considerar os estágios da construção de um modelo de pirâmide (corte de diamante do tipo Pirâmide).
No
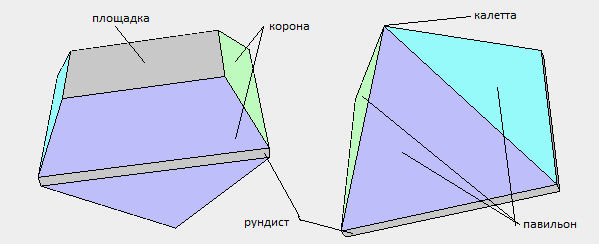
primeiro estágio, precisamos desenhar a vista pretendida do modelo e depois numerar seus vértices. A figura abaixo mostra a numeração dos vértices e os nomes dos elementos de corte incluídos no modelo de corte em pirâmide.

Depois disso, é necessário formar faces a partir dos vértices numerados. Por exemplo, para a face do site e as faces da coroa, escreva a seguinte sequência de vértices (o primeiro vértice duplicado da face indica que a face terminou):
0, 3, 2, 1, 0;
As faces devem estar no sentido anti-horário. O arquivo pyramid_index.js contém o código-fonte para percorrer todas as faces da pirâmide e comentários detalhados. O resultado do rastreamento é gravado na matriz index_cut.
No
segundo estágio, podemos colorir as faces do modelo. Esta etapa é opcional se não precisarmos de uma coloração. Suponha que desejamos colorir um modelo de pirâmide da seguinte maneira:
Para esse propósito, o arquivo pyramid_colors.js é criado no qual a função facet_colors () está localizada, que grava as cores de todas as faces na matriz de cores.
No
terceiro estágio , depois que todos os vértices são numerados e as seqüências transversais de todos os vértices das faces são registradas, é necessário definir os parâmetros do modelo e calcular as coordenadas de todos os seus vértices. Obviamente, supõe-se que já delineamos o algoritmo de construção para nós mesmos e descobrimos como todas as faces do modelo serão localizadas no espaço. Para a pirâmide, escolheremos os seguintes parâmetros, que determinarão os tamanhos de suas partes individuais e de todo o modelo como um todo:
var DEGREE = 0.01745329251994;
A escolha dos parâmetros é determinada pelo desenvolvedor do modelo. Por exemplo, em vez de definir dois parâmetros para dois cantos da coroa, você pode definir um único parâmetro para dois ângulos de uma só vez - então esses ângulos serão sempre os mesmos. Você pode inserir um parâmetro que determina o tamanho do site. Nesse caso, é necessário não definir a altura da coroa ou não a inclinação de suas faces. Outra opção para escolher parâmetros é tornar alguns parâmetros computáveis. Nesse caso, ao alterar alguns parâmetros, outros podem alterar seu valor inicial. Por exemplo, se assumirmos que, para a pirâmide, definimos um parâmetro para definir o ângulo de inclinação das faces coronais, outro parâmetro para a altura da coroa e outro parâmetro que definirá o tamanho da área, ao alterar o ângulo das faces, seremos obrigados a alterar o tamanho da área ou altura da coroa. Por outro lado, se você alterar o parâmetro que define o tamanho do bloco, o valor do parâmetro que define a altura ou a inclinação das faces coronais será alterado automaticamente. A opção associada à aplicação dos parâmetros calculados neste programa, bem como na construção dos outros modelos de corte apresentados no local, não é utilizada.
No
quarto estágio , as coordenadas dos vértices do modelo são calculadas. Os dados iniciais para o cálculo são os valores dos parâmetros do modelo e como imaginamos sua aparência. O arquivo pyramid_verts.js contém o texto de origem (com comentários detalhados) da função de cálculo de vértice do modelo, chamada VerticesCalculation. É com esse cálculo que as funções da biblioteca WebGeometry são usadas nessa função. Os resultados do cálculo das coordenadas dos vértices são inseridos na matriz de vértices. Observe que no programa para encontrar as coordenadas dos vértices, sequências de números separadas são usadas para os vértices que compõem a coroa (quatro vértices), os vértices que compõem a cintura (quatro vértices) e os vértices que compõem o pavilhão (no modelo de pirâmide, apenas o vértice é incluído no pavilhão). Essa escolha de numeração adicional de vértices é usada para facilitar a orientação do programador entre os vértices cortados, uma vez que o número de vértices frequentemente excede 100.
No
quinto estágio, após a conclusão do cálculo das coordenadas dos vértices, é necessário construir programaticamente o poliedro (poliedro) do modelo. Os dados iniciais para sua construção são matrizes criadas anteriormente de index_cut, cores e vértices. Um modelo de poliedro pode ser representado simplesmente como um conjunto de faces que vincula um poliedro no espaço. A função CreatePolyhedron está no arquivo polyhedron.js. Como resultado do trabalho dessa função, é criada uma matriz de polígonos (polígonos), na qual o modelo tridimensional consiste. Cada polígono é descrito pela seguinte função (de fato, é uma função construtora chamada pelo novo operador ao criar um novo polígono):
function Polygon() { this.IndexFacet = [];
Como o WebGL e a biblioteca ThreeJS criada em sua base trabalham com primitivas triangulares, ela é triangulada para cada face do modelo. Supõe-se que todas as faces do modelo são polígonos convexos. Por fim, a função CreatePolyhedron executa todas as etapas necessárias para criar estruturas de dados que descrevem completamente todas as faces do poliedro de forma que possam ser passadas para as funções da biblioteca ThreeJS para exibir o modelo na tela.
No
sexto estágio , o modelo é exibido na tela usando as funções ThreeJS. De maneira padrão, a cena, o renderizador e a câmera são criados. Para examinar o modelo de corte de todos os lados, o programa Pyramid usa o elemento orbitControls. Ao criar outros modelos de corte, para inspecionar cortes de todos os lados, eu não usei orbitControls, mas introduzi a capacidade de girar o próprio modelo. Em seguida, criamos as malhas do modelo. Você pode fazer duas coisas.
No primeiro método, consideramos o modelo de corte como um conjunto de malhas de face separadas. Nesse caso, cada face é um objeto 3D separado. Com essa representação do modelo, o processo de seleção de uma face individual usando o elemento Three.JS, que tem o nome raycaster, é bastante simples. Além disso, esse método pode ser complementado pela criação de malhas de segmentos nas margens de cada face.
Na segunda maneira, consideramos o modelo de corte como um único objeto, representado por apenas uma malha que inclui imediatamente todas as faces do modelo. Este método é conveniente para usar ao exibir um modelo usando shaders. Esse método não é usado no modelo de corte Pyramid, mas é usado para criar modelos de corte Octagon, Brilliant e outros que podem ser vistos no meu site.
No
sétimo estágio , são criados botões e funções anexados a eles que permitem alterar o valor dos parâmetros que determinam a forma e o tamanho do modelo. Quando um botão é pressionado, é chamada uma função que aumenta ou diminui o valor do parâmetro correspondente. Isso significa que é necessário recalcular o valor das coordenadas dos vértices do modelo. Após a recontagem, a correção do modelo recém-construído é verificada. Por exemplo, é determinado se alguns valores estão fora da tolerância. No caso dos modelos de corte com diamante, geralmente se trata de verificar se o corte convexo permanece após a sua reconstrução. A verificação da protuberância é a seguinte. Através de cada face, é desenhado um plano no qual essa face se encontra e, em seguida, é determinada a posição de cada vértice do modelo em relação a esse plano. Todos os vértices devem estar localizados no mesmo lado deste plano. Se o modelo for considerado incorreto, o parâmetro retornará ao seu valor original e o modelo será reconstruído novamente. Para modelos de corte com cinta não convexa (apenas esse elemento de alguns cortes, como Coração, pode ser não convexo), a convexidade é verificada separadamente para a coroa e separadamente para o pavilhão. O rundist, no entanto, é excluído da verificação. Para modelos simples, você pode restringir-se a uma simples verificação de parâmetro. Por exemplo, se estamos construindo um modelo de casa, o teto não deve ter mais do que uma certa altura de antecedência. Portanto, simplesmente definindo a restrição desse parâmetro em magnitude, obtemos o resultado desejado. Depois que os botões de parâmetro são adicionados, é muito desejável exibir visualmente o valor de cada parâmetro quando ele muda depois de clicar no botão. Para isso, é criada uma tela bidimensional em HTML5 e, ao lado do botão correspondente, o valor do parâmetro é exibido nela.
Assim, examinamos todas as etapas da construção de um modelo usando o exemplo da pirâmide. Para a pirâmide (assim como para todos os outros modelos do site), criei outro programa Pyramid_text.html. O exemplo deste programa mostra como você pode exibir texto tridimensional para numerar os vértices de um modelo. Se alguém quiser saber como modelos complexos são criados, considere criar modelos
(consulte GitHub) na seguinte sequência:
Octógono . Um modelo que demonstra a criação de planos de várias maneiras e trabalhando com esses planos. Ao construir um modelo, também são utilizados métodos usados ao trabalhar com vetores e linhas no espaço.
Brilhante . Este é o corte de diamante clássico e mais comum. Alguns elementos da construção de um modelo tridimensional desse corte são usados no futuro ao criar facetas MoonMarquise, MoonPear e Heart. Como é calculada a cinta desse corte, que tem a forma de uma superelipse, é mostrada separadamente no programa BrilliantGirdlt.html. Neste programa, a linha da cintura é construída em uma tela bidimensional (tela).
MoonMarquise . O corte marquise, como o Brilliant, é um dos cortes clássicos em diamante. Diferentemente de uma faceta simples desse tipo (Marquise), as chamadas "facetas da lua" são adicionadas à faceta MoonMarquise do pavilhão. O cortador MoonMarquise é formado por dois arcos de elipses. Uma construção detalhada dessa cinta sobre tela é mostrada no programa MarquiseGirdle.html. O texto deste programa tem comentários detalhados sobre a construção. Observamos um ponto em relação ao cálculo da linha da cintura - ela usa a propriedade de uma tangente a uma elipse. É considerado, por exemplo, no livro "Curso de Geometria Analítica" (o autor deste livro é N.I. Muskhelishvili).
MoonPear A garra cortada MoonPear é formada pelos arcos de três elipses. Sua construção é baseada na construção da cinta de corte Marquise, mas é mais complexa. Para ver a linha da cinta Marquise e como dividir a gundista em segmentos, execute o programa PearGirdle.html.
Coração O corte em “coração” é um dos cortes clássicos, mas possui, em contraste com a maioria dos tipos de corte, um formato de cintura não convexa. O rudista de corte cardíaco é composto por duas cintas de corte de pêra inclinadas uma em relação à outra. Na tela, você pode ver a linha da cintura executando o programa HeartGirdle.html. Construir um corte no coração é um grande desafio.
Cruz de Malta . O cortador do corte “Cruz de Malta” é feito na forma de um “travesseiro” (almofada). Recortes com esse cinto se espalharam recentemente. A linha deste cinto é composta por oito arcos conjugados - quatro arcos principais que limitam o travesseiro em quatro lados e quatro arcos de tamanho menor, emparelhando os arcos principais do travesseiro nos cantos do cinto. Executando os programas CushionGirdle_1.html e CushionGirdle_2.html, é possível ver a forma da linha da cinta, o trabalho de todos os parâmetros que definem sua forma e a divisão da cinta em segmentos.
Estrela pentagonal . O cortador de estrela pentagonal é formado por uma linha com o nome do epitrochoide. O epitrocóide é uma curva relacionada ao ciclóide. No programa Wavy_Pentagon_Girdle.html, alterando os valores dos parâmetros, você pode alterar a "ondulação" da cintura e até mudar o pentágono para um polígono com um número diferente de saliências ("pétalas"). No entanto, deve-se lembrar que o próprio modelo deste corte é construído para o valor do parâmetro "Número de pétalas" igual a 5.
Como mencionado anteriormente, para todos os modelos acima, são criados programas exibindo o número de vértices de corte. Nesses programas, é feita uma alternância entre a exibição de todos os vértices do modelo e a indicação dos números de vértices da coroa, cinta e pavilhão separadamente. Suponha que no modelo de corte maltês você queira criar um plano passando pelos vértices com os números 84, 88 e 145. Em vez de usar esses números para identificar os pontos pelos quais o avião passa ao criar um plano usando a função CreatePlaneThreePoints, uma gravação usando um numeração de picos para o cinto e o pavilhão:
var plane = new Plane3D(); plane.CreatePlaneThreePoints(girdle[68], girdle[72], crown[1]);
Note-se que os programas que exibem números de vértices do modelo funcionam muito lentamente (pelo menos no meu computador). Pode levar alguns segundos até que a saída dos números dos vértices do modelo seja concluída.
Para resumir tudo isso, na minha opinião, a escolha de poliedros (modelos de corte) para demonstrar a operação de funções geométricas é uma das melhores opções. Tendo examinado o trabalho dos exemplos acima, podemos prosseguir com a criação de objetos geométricos relacionados a campos de atividade completamente diferentes dos da modelagem do corte de diamante.