Solução numérica de modelos matemáticos de objetos dados por sistemas de equações diferenciais

Introdução:

Na modelagem matemática de vários dispositivos técnicos, são utilizados sistemas de equações diferenciais não lineares. Tais modelos são usados ​​não apenas em tecnologia, mas também em economia, química, biologia, medicina e administração.

O estudo do funcionamento de tais dispositivos requer a solução desses sistemas de equações. Como a maior parte dessas equações é não linear e não estacionária, muitas vezes é impossível obter sua solução analítica.

É necessário usar métodos numéricos, o mais famoso dos quais é o método Runge - Kutta [1]. Quanto ao Python, em publicações sobre métodos numéricos, por exemplo [2,3], há muito poucos dados sobre o uso de Runge - Kutta, e não há dados sobre sua modificação no método Runge - Kutta - Felberg.

Atualmente, graças à sua interface simples, a função odeint do módulo scipy.integrate tem a maior distribuição no Python. A segunda ode de função deste módulo implementa vários métodos, incluindo o mencionado método Runge-Kutta-Felberg de cinco níveis, mas, devido à sua universalidade, possui desempenho limitado.

O objetivo desta publicação é uma análise comparativa dos meios listados para resolver numericamente sistemas de equações diferenciais com um autor modificado sob Python usando o método Runge-Kutta-Felberg. A publicação também fornece soluções para problemas de valor-limite para sistemas de equações diferenciais (SDEs).

Breves dados teóricos e reais sobre os métodos e softwares considerados para a solução numérica do CDS

Problema de Cauchy

Para uma equação diferencial de enésima ordem, o problema de Cauchy consiste em encontrar uma função que satisfaça a igualdade:



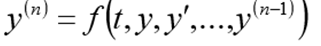
e condições iniciais



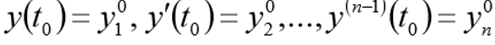
Antes de resolver este problema, deve ser reescrito na forma do seguinte CDS

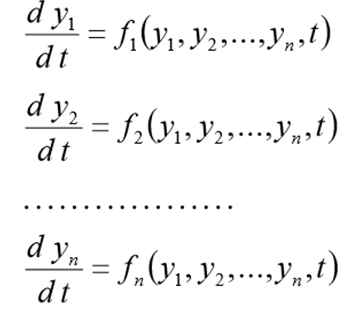
(1)

com condições iniciais



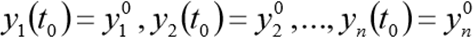Módulo Scipy.integrate

O módulo possui duas funções ode () e odeint (), projetadas para resolver sistemas de equações diferenciais ordinárias (ODEs) de primeira ordem com condições iniciais em um ponto (problema de Cauchy). A função ode () é mais universal e a função odeint () (integrador de ODE) possui uma interface mais simples e resolve a maioria dos problemas.

Função Odeint ()

A função odeint () possui três argumentos obrigatórios e muitas opções. Ele tem o seguinte formato odeint (func, y0, t [, args = (), ...]) O argumento func é o nome do Python da função de duas variáveis, a primeira das quais é a lista y = [y1, y2, ..., yn ] e o segundo é o nome da variável independente.

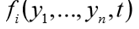
A função Func deve retornar uma lista de n valores de função para um dado valor do argumento independente t. De fato, a função func (y, t) implementa o cálculo do lado direito do sistema (1).

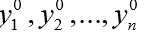
O segundo argumento y0 de odeint () é uma matriz (ou lista) de valores iniciais em t = t0.

O terceiro argumento é uma matriz de pontos no tempo em que você deseja obter uma solução para o problema. Nesse caso, o primeiro elemento dessa matriz é considerado como t0.

A função odeint () retorna uma matriz de tamanho len (t) x len (y0). A função odeint () possui muitas opções que controlam sua operação. As opções rtol (erro relativo) e atol (erro absoluto) determinam o erro de cálculo ei para cada valor de yi de acordo com a fórmula



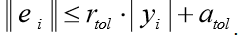
Eles podem ser vetores ou escalares. Por padrão



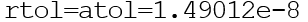Função Ode ()

A segunda função do módulo scipy.integrate, projetada para resolver equações e sistemas diferenciais, é denominada ode (). Ele cria um objeto ODE (digite scipy.integrate._ode.ode). Tendo um link para esse objeto, deve-se usar seus métodos para resolver equações diferenciais. Da mesma forma que a função odeint (), a função ode (func) envolve reduzir o problema a um sistema de equações diferenciais da forma (1) e usar sua função do lado direito.

A única diferença é que a função do lado direito func (t, y) aceita uma variável independente como o primeiro argumento e a lista de valores das funções desejadas como o segundo. Por exemplo, a seguinte sequência de instruções cria uma ODE que representa uma tarefa Cauchy.

Método Runge - Kutta

Ao construir algoritmos numéricos, assumimos que existe uma solução para esse problema diferencial, ele é único e possui as propriedades de suavidade necessárias.

Na solução numérica do problema de Cauchy

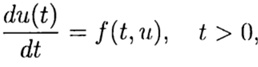
2)

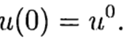
(3)

de acordo com a solução conhecida no ponto t = 0, é necessário encontrar uma solução da equação (3) para outro t. Na solução numérica do problema (2), (3), usaremos uma grade uniforme, por simplicidade, na variável t com uma etapa t> 0.

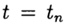
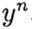
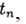
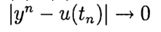
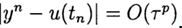
Uma solução aproximada para o problema (2), (3) no ponto denotar . O método converge em um ponto se às . O método possui uma ordem de precisão enésima, se , p> 0 para . O esquema de diferenças mais simples para uma solução aproximada do problema (2), (3) é

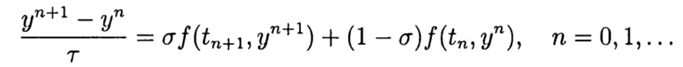
4)

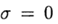
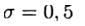
At temos um método explícito e, nesse caso, o esquema de diferenças aproxima a equação (2) com a primeira ordem. Design simétrico em (4) tem uma segunda ordem de aproximação. Esse esquema pertence à classe dos implícitos - para determinar a solução aproximada em uma nova camada, é necessário resolver o problema não linear.

É conveniente construir esquemas explícitos de aproximação de segunda e alta ordem com base no método preditor-corretor. No estágio do preditor (previsão), um esquema explícito é usado.

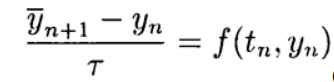
(5)

e no estágio corretor (refinamento), um diagrama



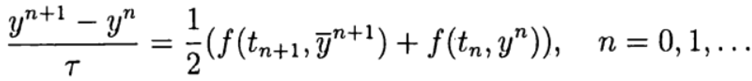
Nos métodos Runge - Kutta de uma etapa, as idéias do preditor-corretor são realizadas de maneira mais completa. Este método é escrito em forma geral:

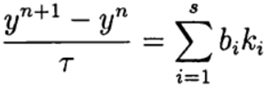
(6)

onde



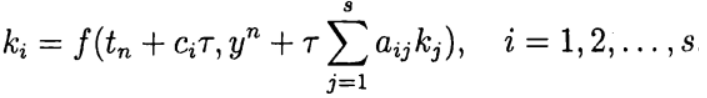
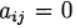
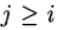
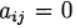
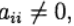
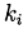
A fórmula (6) é baseada nos cálculos de s da função f e é chamada de estágio s. Se às nós temos o método Runge - Kutta explícito. Se para j> 1 e então determinado implicitamente a partir da equação:

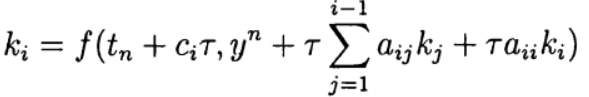
(7)

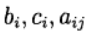
Esse método de Runge-Kutta é mencionado como diagonalmente implícito. Parâmetros determine uma variante do método Runge - Kutta. A seguinte representação do método é usada (tabela Butcher)



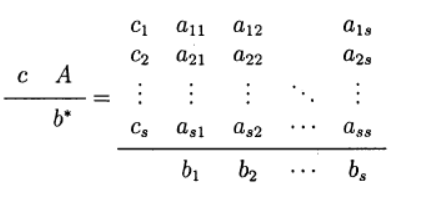
Um dos mais comuns é o método Runge - Kutta explícito de quarta ordem.

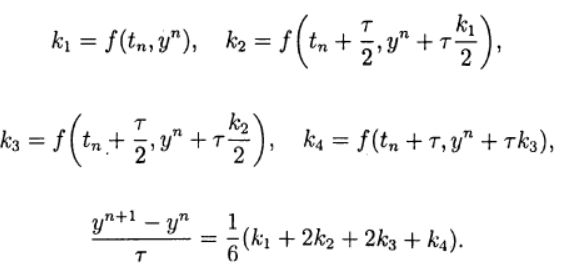
(8)

Método Runge - Kutta - Felberg

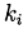
Dou o valor dos coeficientes calculados método

(9)

Em vista de (9), a solução geral tem a forma:

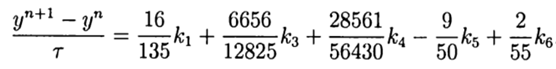
(10)

Esta solução fornece a quinta ordem de precisão, resta adaptá-la ao Python.

Experiência computacional para determinar o erro absoluto da solução numérica de uma equação diferencial não linear 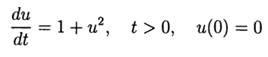usando as duas funções def odein (), def oden () do módulo scipy.integrate e os métodos Runge - Kutta e Runge - Kutta - Felberg adaptados ao Python

Temos:









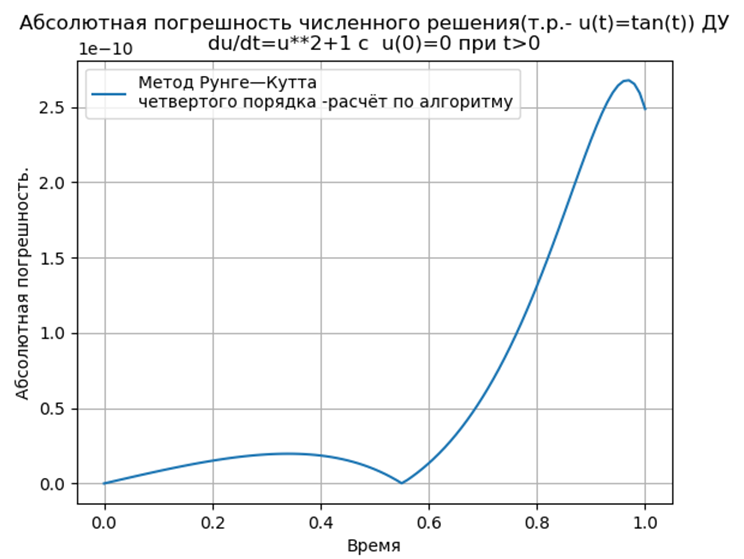
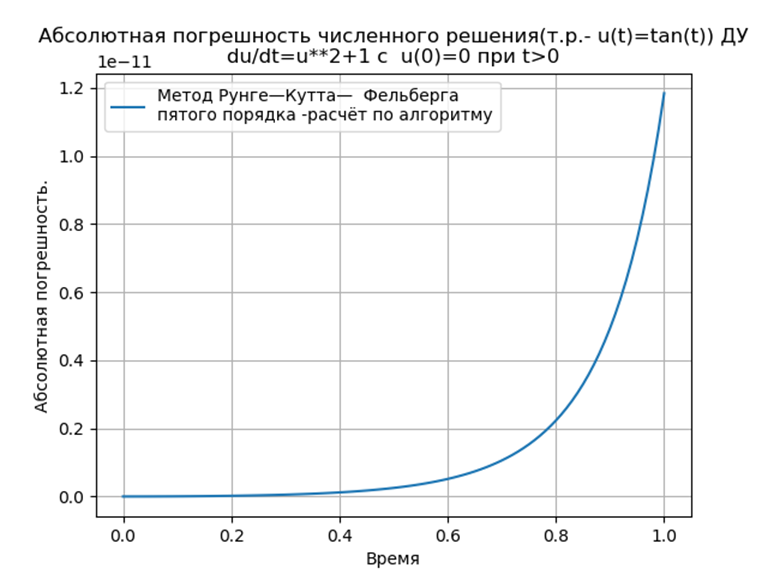
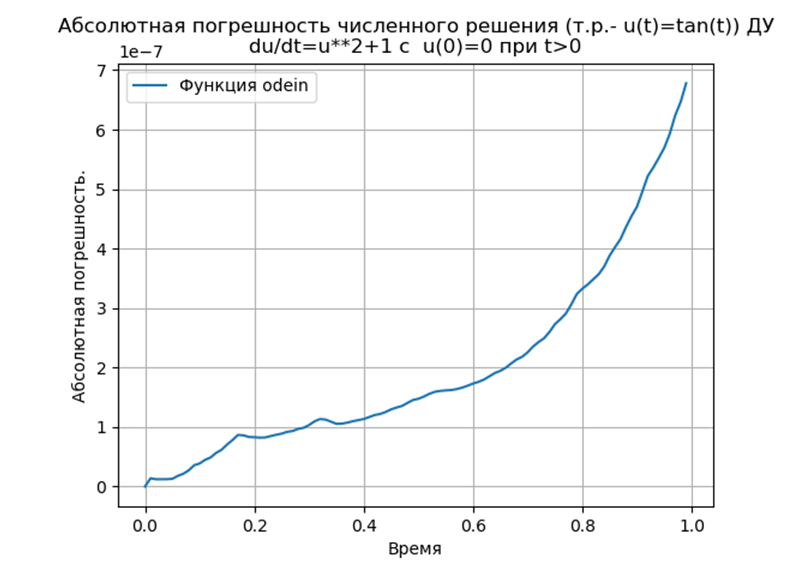
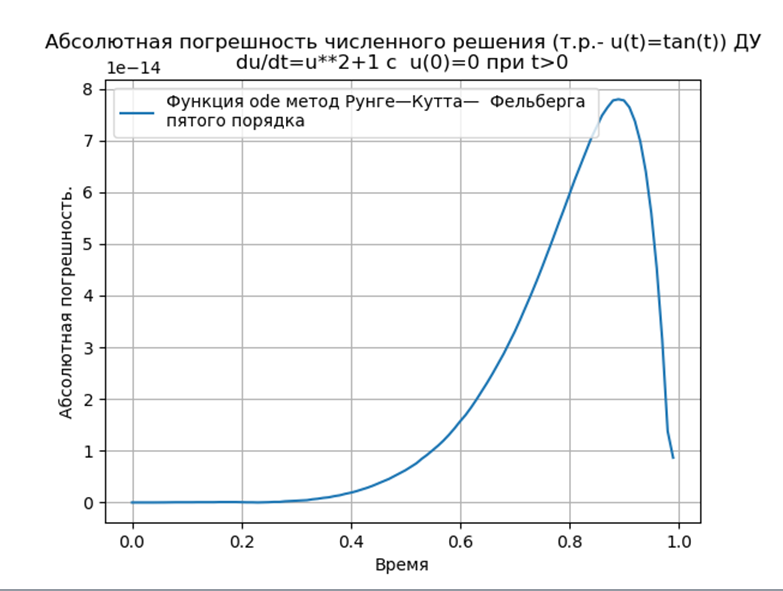Conclusão:

Os métodos Runge - Kutta e Runge - Kutta - Felberg adaptados ao Python têm um absoluto mais baixo que uma solução usando a função odeint, mas mais que uma solução usando a função edu. É necessário realizar um estudo de desempenho.

Um experimento numérico comparando a velocidade da solução numérica de SDEs usando a função ode com o atributo dopri5 (método Runge - Kutta da 5ª ordem) e usando o método Runge - Kutta - Felberg adaptado ao Python

Uma análise comparativa é realizada usando o problema do modelo dado em [2] como exemplo. Para não repetir a fonte, apresentarei a formulação e solução do problema do modelo de [2].

Vamos resolver o problema de Cauchy, que descreve o movimento de um corpo lançado com uma velocidade inicial v0 em um ângulo α em relação ao horizonte, pressupondo que a resistência do ar seja proporcional ao quadrado da velocidade. Na forma vetorial, a equação do movimento tem a forma



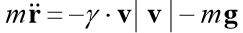
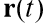
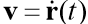
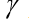
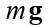
onde É o raio do vetor do corpo em movimento, É o vetor de velocidade do corpo, - coeficiente de arrasto, vetor forças do peso corporal da massa m, g - aceleração da gravidade.



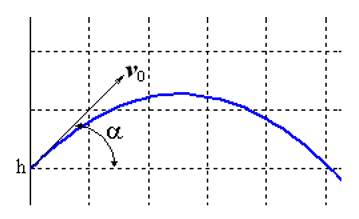
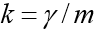
A peculiaridade dessa tarefa é que o movimento termina em um ponto anteriormente desconhecido no tempo em que o corpo cai no chão. Se designado , então, na forma de coordenadas, temos um sistema de equações:



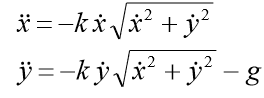
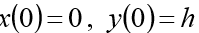
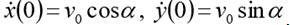
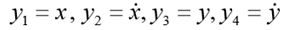
As condições iniciais devem ser adicionadas ao sistema: (h altura inicial) . Coloque . Em seguida, o sistema ODE de primeira ordem correspondente assume a forma:



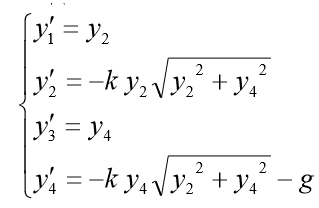
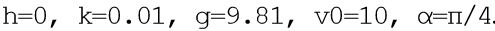
Para o problema do modelo, colocamos . Omitindo uma descrição bastante extensa do programa, darei apenas uma lista dos comentários aos quais, penso eu, o princípio de sua operação será claro. O programa adicionou uma contagem regressiva para análise comparativa.



Temos:

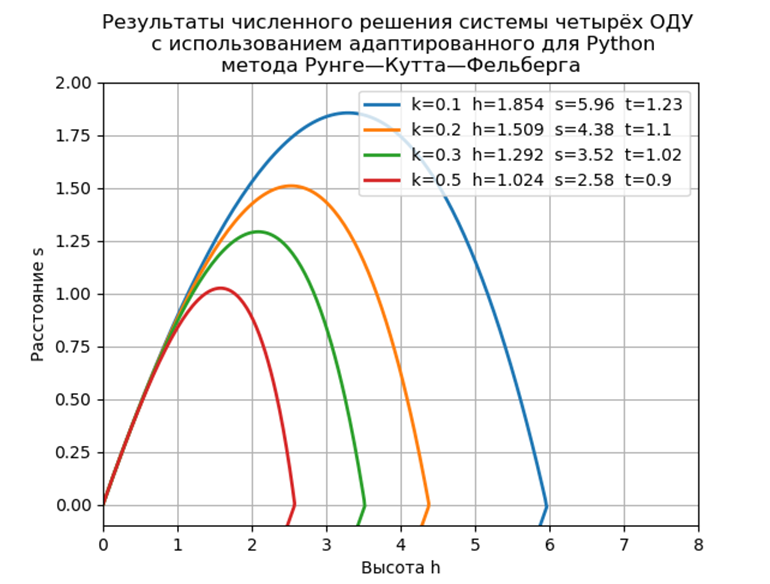
Tempo de voo = 1,2316 Distância = 5,9829 Altura = 1,8542
Tempo de voo = 1.1016 Distância = 4.3830 Altura = 1.5088
Tempo de voo = 1.0197 Distância = 3.5265 Altura = 1.2912
Tempo de voo = 0.9068 Distância = 2.5842 Altura = 1.0240
Tempo para o problema do modelo: 0,445787



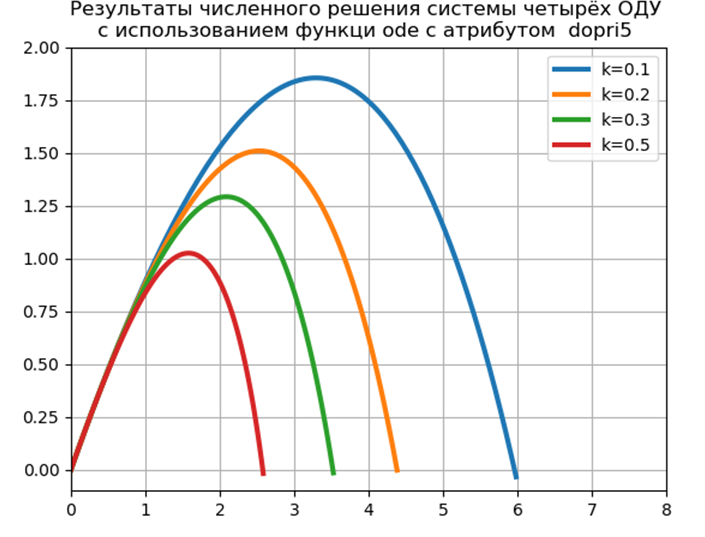
Para implementar uma solução numérica do CDS usando ferramentas Python sem usar módulos especiais, propus e investiguei a seguinte função:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

A função de incremento (f, t, y, tau) fornece a quinta ordem do método de solução numérica. Outros recursos do programa podem ser encontrados na seguinte listagem:


Temos:

Tempo para o problema do modelo: 0,259927



Conclusão

A implementação de software proposta para o problema do modelo sem o uso de módulos especiais tem desempenho quase duas vezes mais rápido do que com a função ode, mas não devemos esquecer que o ode possui uma precisão mais alta da solução numérica e a possibilidade de escolher um método de solução.

Resolvendo um problema de valor limite com condições de limite separadas por encadeamento

Damos um exemplo de um problema específico de valor-limite com condições de limite separadas por thread:

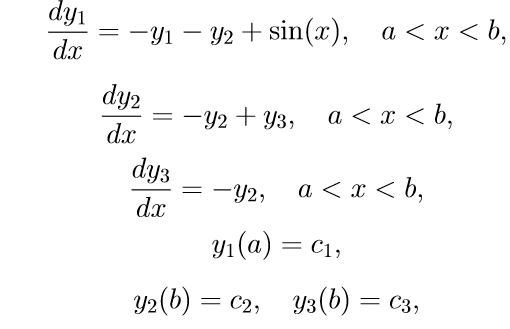
(11)

Para resolver o problema (11), usamos o seguinte algoritmo:

1. Resolvemos as três primeiras equações não homogêneas do sistema (11) com as condições iniciais

Introduzimos a notação para resolver o problema de Cauchy:


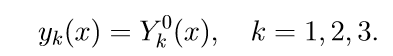
2. Resolvemos as três primeiras equações homogêneas do sistema (11) com as condições iniciais

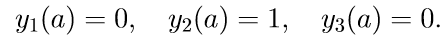
Introduzimos a notação para resolver o problema de Cauchy:


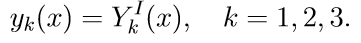
3. Resolvemos as três primeiras equações homogêneas do sistema (11) com as condições iniciais



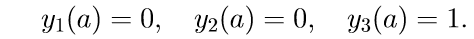
Introduzimos a notação para resolver o problema de Cauchy:



4. A solução geral do problema do valor-limite (11) usando as soluções dos problemas de Cauchy é escrita como uma combinação linear de soluções:

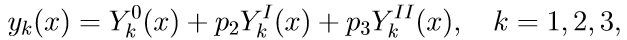
onde p2, p3 são alguns parâmetros desconhecidos.

5. Para determinar os parâmetros p2, p3, usamos as condições de contorno das duas últimas equações (11), ou seja, as condições para x = b. Substituindo, obtemos um sistema de equações lineares em relação ao desconhecido p2, p3:
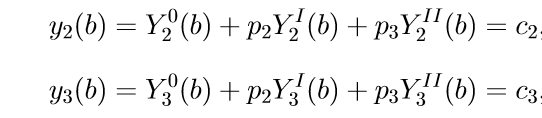
(12)
Resolvendo (12), obtemos as relações para p2, p3.

Usando o algoritmo acima, usando o método Runge - Kutta - Felberg, obtemos o seguinte programa:


Temos:

y0 [0] = 0,0
y1 [0] = 1,0
y2 [0] = 0,7156448588231397
y3 [0] = 1,324566562303714
y0 [N-1] = 0,9900000000000007
y1 [N-1] = 0,1747719838716767
y2 [N-1] = 0,8
y3 [N-1] = 0,5000000000000001
Tempo para o problema do modelo: 0,070878

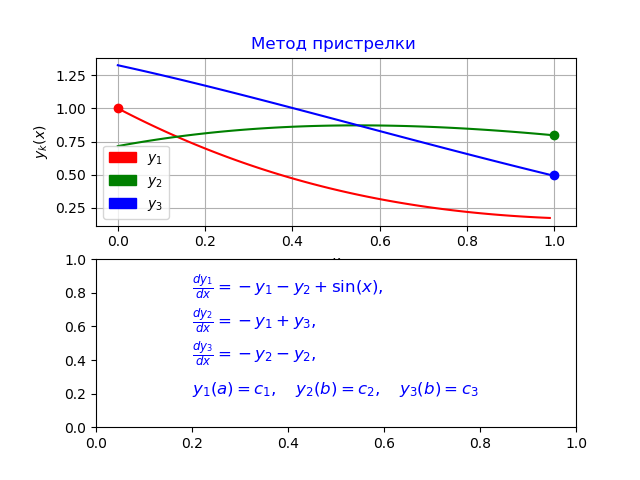
Conclusão

O programa desenvolvido por mim difere do erro dado em [3], que confirma a análise comparativa da função odeint fornecida no início do artigo com o método Runge - Kutta - Felberg implementado em Python.

Referências:

1. Solução numérica de modelos matemáticos de objetos definidos por sistemas compostos de equações diferenciais.

2. Introdução ao Python científico.

3. N.M. Polyakova, E.V. Shiryaeva Python 3. Criando uma interface gráfica do usuário (usando o exemplo de solução do problema de valor-limite para equações diferenciais ordinárias lineares pelo método de disparo). Rostov do Don 2017.