Manipulador "Manual"

Certa vez, durante o meu segundo ano na universidade, recebi a tarefa: cozinhar algo "mais ou menos" para confirmar a alta patente de "futuro engenheiro de robótica". Nesta nota pathos, entrei nas profundezas da consciência em busca de idéias. Após uma curta viagem, surgiu uma idéia sobre o dispositivo, cuja teoria da criação eu quero compartilhar com o público.

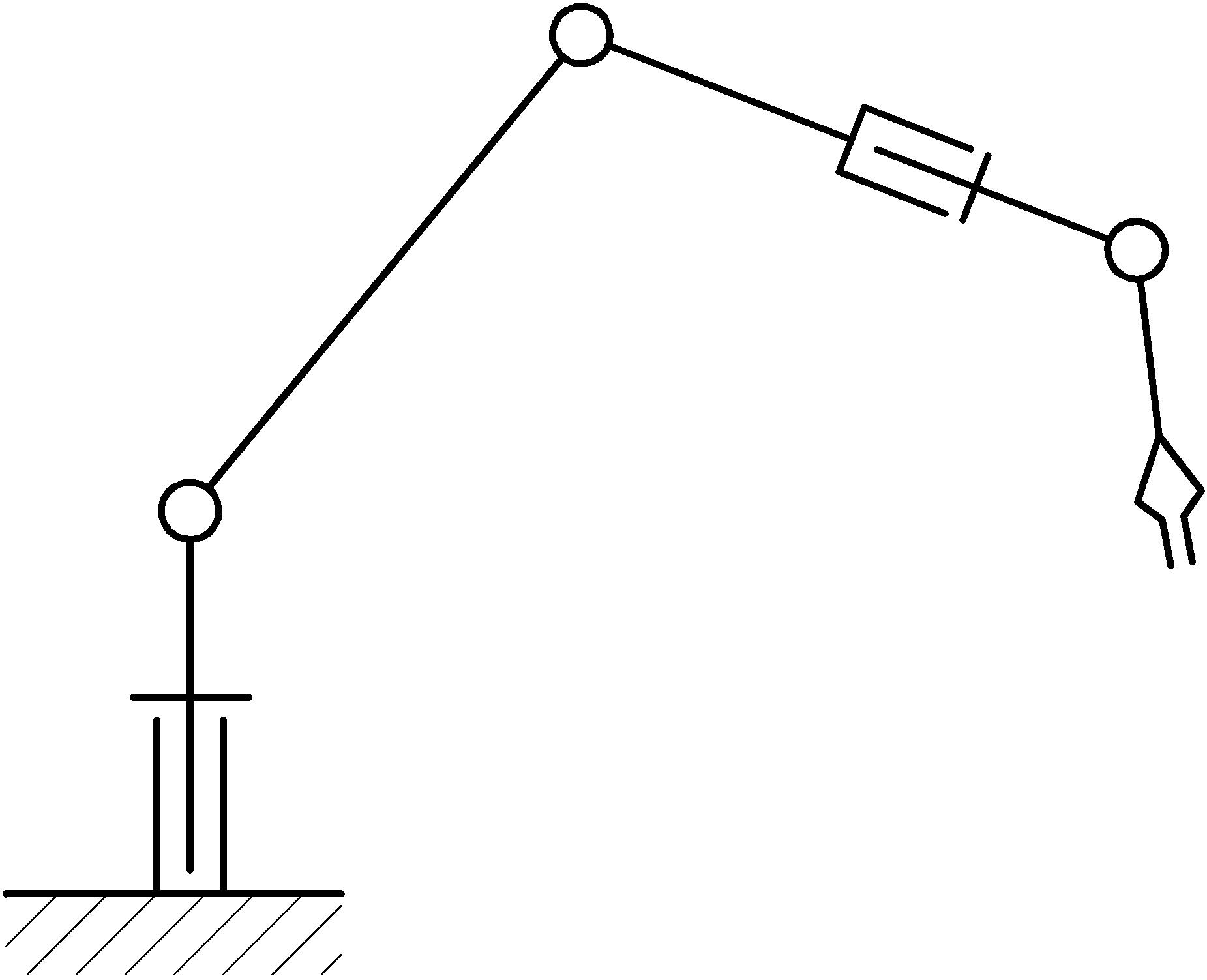
A essência do desenvolvimento é essa. Considere o habitual, digamos, manipulador de 5 eixos (o diagrama estrutural cinemático é mostrado na figura abaixo). Suas capacidades ao se mover no espaço são amplas: é capaz de fazer movimentos em 5 coordenadas e, ao mesmo tempo, ou seja, 3 coordenadas ao longo dos três eixos XYZ e rotação em torno de dois deles. Nesse caso, o elemento de trabalho do manipulador é capaz de ocupar qualquer posição no espaço de trabalho e, ao mesmo tempo, manter a orientação necessária do corpo de trabalho (sem contar a rotação do elemento de trabalho em torno de seu próprio eixo).



Este projeto refere-se a manipuladores de um tipo antropomórfico e, portanto, é capaz, aproximadamente, é claro, de reproduzir o movimento de uma mão humana. Discutindo sobre esta tese, surgiu a ideia de que seria interessante fazer o manipulador copiar remotamente os movimentos da minha mão em tempo real. Para que eu apenas coloque um sensor na minha mão que leia os movimentos da mão (linear e angular), e essa coisa mecânica os repetirá depois de mim. Como o manipulador pode executar as funções de mover e orientar o corpo de trabalho, com a ajuda da mão uma pessoa pode mover e orientar a palma da mão, portanto, esses dois processos são semelhantes e podem ser representados como um processo comum - captura do movimento da mão pelo manipulador em tempo real.


Isso completa a declaração do problema. Agora vamos analisar a tarefa (o idioma não é chamado de "tarefa técnica"). É necessário desenvolver dois dispositivos estruturalmente independentes: o próprio manipulador e o dispositivo de rastreamento de movimento, montado no braço. Isso será seguido pelo processo demorado de criar descrições matemáticas, compilar um algoritmo e escrever um software. Dividimos o projeto em três partes:

1. O desenvolvimento do manipulador
2. Desenvolvimento de um dispositivo para rastrear o movimento do braço
3. Tudo o resto

Brevemente sobre cada uma das etapas:

1. Tudo aqui é trivial ... No CAD, projetamos a estrutura, realizamos desenhos de peças e fabricamos e montamos. Depois calculamos a cinemática e escrevemos nosso próprio software, que ocultará as chamadas de baixo nível para as unidades.
2. Nesta fase, determinamos o tipo de sensores, projetamos um diagrama de circuito, fabricamos uma placa de circuito impresso, desenvolvemos um algoritmo para determinar a posição no espaço, escrevemos software.
3. Na verdade, por quais eram as etapas anteriores - fazer o manipulador obedecer ao proprietário. Aqui desenvolvo um algoritmo para converter coordenadas no campo de trabalho do manipulador.

1. O desenvolvimento do manipulador

Neste projeto, como mencionado acima, usamos um manipulador com 5 graus de liberdade. Esse número de graus de liberdade é suficiente, porque eles incluem três deslocamentos lineares e dois rotacionais. Os dois últimos são necessários para a orientação do corpo de trabalho, pois a direção do PO no espaço pode ser especificada na forma de um vetor, e o vetor pode ser definitivamente restaurado a partir de dois ângulos de rotação (sem levar em consideração o comprimento). Nesse caso, precisamos de cinco coordenadas generalizadas, iguais ao número de eixos.

Os elos do manipulador são conectados por pares cinemáticos rotacionais da quinta classe. O design do manipulador é padrão para o seu tipo (o esquema cinemático é apresentado no início do artigo). Possui um leito fixo, com o qual o sistema básico de coordenadas está conectado, um suporte rotativo, ao qual os elos móveis restantes estão conectados, conectados em uma corrente. Um corpo de trabalho é anexado ao elo final (flange), neste caso, sua imitação na forma de um ponteiro em forma de seta (veja a imagem abaixo).




O modelo 3D foi construído em CAD "Compass 3D". Material das peças - madeira compensada de 4 mm e PLA para peças de plástico. Peças de madeira compensada foram cortadas em uma máquina a laser, peças de plástico foram impressas em uma impressora 3D. Os servos digitais Dynamixel AX-12 são usados ​​como unidades de eixo. A aparência do manipulador se assemelha a um inseto vil, do qual ele recebeu o apelido "Komar".

A descrição matemática da cinemática

Nesta fase, é necessário calcular a cinemática direta e inversa do manipulador. A tarefa direta é determinar a posição dos links em relação a algum sistema básico de coordenadas usando os valores conhecidos das coordenadas generalizadas (neste caso, os ângulos de rotação dos links). A tarefa inversa a ela é denominada cinemática inversa ou inversa, consiste em determinar os parâmetros das coordenadas generalizadas para atingir a posição e orientação desejadas do corpo de trabalho do manipulador.

Vamos começar calculando a cinemática inversa. Vamos descrever o esquema geométrico do manipulador, a partir do qual as relações geométricas de interesse para nós serão claras.



A posição requerida é representada por um vetor de raio $$$\ vec {r}$ . Vale a pena explicar por que o vetor $$$\ vec {r}$ atraído para o ponto do flange e não para o ponto final da RO. Como a orientação do corpo de trabalho é conhecida por nós com antecedência (eu mesmo a determino de acordo com alguns requisitos), é necessário que o ponto do flange esteja no lugar certo, indicado como vetor $$$\ vec {r}$ . Esse vetor é obtido subtraindo o vetor raio $$$\ vec {R}$ atraídos para o ponto final da PO, seu vetor de orientação $$$\ vec {v_0}$ , em relação ao BSK, ou seja:

$$

$$\ vec {r} = \ vec {R} - \ vec {v_0}$$

Considere a transição do ponto do flange para a posição desejada. É realizada pela rotação dos elos aeb (eu os descrevi na forma de vetores) nas dobradiças A , B e C. A origem do sistema de coordenadas base (BSC) é colocada no ponto da dobradiça B. O eixo de rotação da dobradiça A é direcionado ao longo do eixo Z , os eixos B e C são direcionados perpendicularmente a Z.

Quando todas as formalidades forem cumpridas, vamos direto ao ponto. Para resolver o problema da cinemática inversa, usei uma abordagem geométrica devido à simplicidade do design do manipulador. Pela geometria, pode-se ver que o vetor $$$\ vec {r}$ igual à soma dos vetores de link $$$\ vec {a}$ e $$$\ vec {b}$ . Ângulos $$$\ theta$ , $$$\ gamma_1$ , $$$\ gamma_2$ - os ângulos de rotação dos elos A , B e C, respectivamente.
Considere um triângulo delimitado por vetores $$$\ vec {r}$ , $$$\ vec {a}$ e $$$\ vec {b}$ . A partir deste triângulo, pelo teorema do cosseno, encontramos os ângulos $$$\ alpha$ e $$$\ beta$ . Seja o comprimento dos vetores igual a:

$$

$$| \ vec {r} | = r \ quad | \ vec {a} | = a \ quad | \ vec {b} | = b$$

Escrevemos o teorema do cosseno em relação aos ângulos desejados:

$$

Expresse os ângulos $$$\ alpha$ e $$$\ beta$ :

$$

$$\ alpha = \ arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ar} \ right) \ quad \ beta = \ arccos \ left (\ frac {a ^ 2 + b ^ 2 -r ^ 2} {2ab} \ right)$$

Pode ser visto no diagrama geométrico que:

$$

$$\ theta = \ arctan = \ left (\ frac {r_y} {r_x} \ right) \ quad \ omega = \ arcsin = \ left (\ frac {r_z} {r} \ right)$$

Então:

$$

$$\ gamma_1 = \ omega + \ alpha \ quad \ gamma_2 = 180 ^ \ circ- \ beta$$

Finalmente, a transição de uma coordenada linear para os ângulos de rotação dos elos é realizada pelas fórmulas:

$$

$$\ theta = arctan \ left (\ frac {r_y} {r_x} \ right) \\ \ gamma_1 = arcsin \ left (\ frac {r_z} {r} \ right) + arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ab} \ right) \\ \ gamma_2 = 180 ^ \ circ-arccos \ left (\ frac {a ^ 2 + b ^ 2-r ^ 2} {2ar} \ right)$$

Agora que você moveu o ponto do flange para a posição desejada, é necessário orientar adequadamente o corpo de trabalho. Para fazer isso, você precisa conhecer as coordenadas do vetor $$$\ vec {v}$ em relação ao ponto de flange, ou seja, coordenadas com base no sistema local de coordenadas (LSC) - $$${E '}$ , cujo início está localizado no ponto de flange do manipulador.

$$

$$E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

Vetor $$$\ vec {x} '$ dirigido pelo link b , vetor $$$\ vec {y} '$ - ao longo do eixo do giro f1 .
Para encontrar uma base $$$E '$ definimos a matriz de transição do BSK (com base $$$E_0$ ) e LSK. Essa matriz é obtida por uma combinação de rotações nas dobradiças A , B e C :

$$

$$E '= CE_0$$

onde

$$

$$C = R_CR_BR_A$$

Porque matriz $$$E_0$ é único, então:

$$

$$E '= C = R_CR_BR_A$$

Matrix $$$C$ é calculado multiplicando as matrizes de rotação em torno do eixo por um ângulo .
Definimos uma função que calcula essa matriz:

$$

$$f = axisAngle2rotMat (eixo, ângulo)$$

O eixo é tomado na forma de um vetor como uma coluna da matriz obtida por rotações anteriores, e os ângulos já estão calculados acima.

$$

$$C_A = axisAngle2rotMat (E_0 ^ {\ langle3 \ rangle}, \ theta) \\ C_ {BA} = R_BC_A = axisAngle2rotMat (C_A ^ {\ langle2 \ rangle}, \ gamma_1) C_A \\ C_ {CBA} = R_CC_ { BA} = axisAngle2rotMat (C_ {BA} ^ {\ langle2 \ rangle}, \ gamma_1) C_ {BA}$$

Como resultado, obtemos:

$$

$$C = C_ {CBA} \ quad E '= C$$

Deixe o vetor do corpo de trabalho em BSK $$$\ vec {v_0}$ . Então a igualdade é verdadeira:

$$

$$\ vec {v_0} = E '\ vec {v}$$

A partir daqui, expressamos $$$\ vec {v}$ - vetor do corpo de trabalho na base $$$E '$ , ou seja, em relação ao ponto do flange:

$$

$$\ vec {v} = E '^ T \ vec {v_0}$$

Agora, conhecendo o vetor PO, podemos calcular os ângulos de rotação dos eixos orientadores f1 e f2


Para mover o pedido para uma determinada posição, é necessário fazer uma rotação nos cantos $$$\ varphi_1$ e $$$\ varphi_2$ . A figura mostra que

$$

$$\ varphi_1 = arctan \ left (\ frac {v_y} {v_z} \ right) \ quad \ varphi_2 = arcsin \ left (\ frac {\ sqrt {v_y ^ 2 + v_z ^ 2}} {V} \ right)$$

onde $$$V = | \ vec {v} | = \ sqrt {v_x ^ 2 + v_y ^ 2 + v_z ^ 2}$ - o comprimento do corpo de trabalho,
$$$v_x, v_y, v_z$ - coordenadas vetoriais $$$\ vec {v}$ .

O software do manipulador é dividido em dois níveis, superior e inferior. O nível superior é escrito no Matlab na forma de uma biblioteca e vários métodos de comando, o inferior - no microcontrolador Atmega328. A tarefa do nível superior é formular os comandos enviados ao microcontrolador. Sua tarefa é reunir a equipe e, de acordo com ela, instalar as unidades na posição correta. Dessa forma, o sistema de controle mostrou-se confiável (até o momento ...) e conveniente de usar.


A formulação do comando e o envio a partir do nível superior é o seguinte: o usuário na janela de comando Matlab chama uma função da biblioteca (por exemplo, a função de simplesmente mover-se para um ponto), indica os argumentos necessários (geralmente essas são as coordenadas e a orientação do OP). Após as considerações matemáticas descritas acima, registradas na biblioteca, são calculados os ângulos de rotação dos eixos e, se necessário, a velocidade de rotação. Após um protocolo simples, montamos o comando e o enviamos para o microcontrolador de nível inferior via porta COM serial.

Algumas palavras sobre a biblioteca escrita. Tem as seguintes funções à sua disposição:

1. funções de conexão serial
2. funções móveis

• até certo ponto, com uma velocidade constante de todas as unidades
• até um ponto, com uma parada final de todos os inversores (a velocidade do inversor é selecionada proporcionalmente ao seu próprio e maior ângulo de rotação. Assim, no final da aproximação ao ponto, todos os inversores param de se mover)
• até certo ponto, com um movimento suave de cada acionamento (nesse caso, o gráfico de velocidade se parece com um trapézio com áreas de aceleração, velocidade constante e frenagem)
  
  
  Graph

  

  
  
  
  
• até um ponto, de acordo com os ângulos de rotação especificados manualmente dos eixos e a velocidade de rotação

É claro que a lista de funções pode ser expandida, mas essa funcionalidade foi suficiente para resolver diretamente o problema para o qual o manipulador foi projetado.

O vídeo demonstra a operação do manipulador.

2. Desenvolvimento de um dispositivo para rastrear o movimento do braço

Vá para o próximo passo. Aqui você precisará criar um dispositivo especial que possa rastrear em tempo real a posição na palma da sua mão. Além disso, esse processo é chamado de "captura de movimento". Para implementar o plano, decidi usar o sistema de navegação inercial com amarração (SINS) baseado em três sensores: um giroscópio, acelerômetro e magnetômetro. Um monte desses sensores é chamado IMU - um sensor (na tradução, esse é o mesmo SINS).

Primeiro, projetei uma placa de circuito impresso com a funcionalidade necessária, na qual coloquei esses três sensores. Como controlador de processamento, escolhi (ou melhor, peguei o que era) o microcontrolador Atmega2560. Sensores usados ​​comuns e baratos no mercado chinês. Estes são sensores emparelhados giroscópio de três eixos e acelerômetro MPU6050 e magnetômetro HMC5883l.



O algoritmo para calcular a posição no espaço é bastante simples: primeiro, determinamos a orientação na forma de uma base para o sistema de coordenadas locais (LSC), que é conectado aos sensores e, finalmente, à palma da mão.



A orientação é determinada em relação ao sistema de coordenadas inicial (NSC), que é essencialmente a posição inicial do dispositivo no momento da inicialização. As bases do NSC e LSC consistem em vetores de colunas de seus orth:

$$

$$E_0 = \ left [\ vec {X} \ \ vec {Y} \ \ vec {Z} \ right] = \ left [\ begin {array} {cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \\ E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

Eles estão relacionados pela razão:

$$

$$E '= CE_0$$

Onde $$$C$ É uma matriz de transição, é também uma matriz de rotação no espaço. Consideramos a base do NSC como a matriz de identidade. Portanto,

$$

$$E '= C$$

.
Depois, o vetor de aceleração $$$\ vec {A}$ , que é conhecido em relação ao LSC, deve ser determinado no NSC. Isso é feito multiplicando o vetor da coluna de aceleração pela base LSC:

$$

$$\ vec {A} = E '\ vec {A}'$$

Em seguida, integramos o vetor de aceleração obtido duas vezes ao longo do tempo e obtemos a distância, ou seja, coordenadas:

$$

$$\ vec {r} = \ iint \ vec {A} dt$$

As primeiras tentativas de implementar esse algoritmo foram muito ingênuas ... A ingenuidade foi que eu considerei possível apenas do giroscópio, usando integração discreta, obter uma matriz de rotação em torno do eixo. O eixo, neste caso, pode ser considerado como um pseudovetor de velocidade angular, cujos componentes (projeção no eixo) são a saída do sensor giroscópio. E o ângulo, por sua vez, é obtido através da integração do módulo vetorial. O entusiasmo inicial e o entusiasmo desapareceram quando vi um tamanho monstruoso, o chamado “desvio zero”, causado pelo erro acumulado devido ao erro de integração discreta e ao ruído intrínseco do sensor. Mesmo assim, pensei que, de acordo com o acelerômetro, que em repouso mostra o vetor, o inverso do vetor de aceleração da gravidade (doravante denominado vetor de gravidade), é possível fazer a correção da matriz, mas aqui há incerteza associada ao fato de que a correção é possível somente até a rotação do ângulo em torno do eixo Z. A correção será concluída se for possível restaurar a matriz de rotação de uma maneira alternativa, ou seja, sem usar dados de giroscópio.


Então é necessário usar outro fator pelo qual será possível fazer um ajuste completo da situação. Esse fator é o campo magnético da Terra, que, juntamente com a gravidade em um único ponto do planeta, não muda com o tempo (é claro, a curto prazo). É medido usando o sensor HMC5883l acima mencionado. Nesse caso, temos dois vetores, que são suficientes para determinar a posição no espaço em relação a eles.

Agora surge uma pergunta lógica - "como fazer isso?" Após tentativas frustradas de responder a essa pergunta, subi na Internet pessoalmente, onde encontrei as informações necessárias. A tarefa de determinar a orientação no espaço de acordo com três medidas (velocidade angular, vetor de gravidade e vetor de campo magnético) também surge no design de aeronaves amadoras (por exemplo, helicópteros), de modo que esse problema foi resolvido repetidamente por vários métodos. Um método popular é o chamado filtro Majwick (Sebastian OH Madgwick). Depois de ler o artigo original e não entender o inglês, virei-me para uma tradução maravilhosa (obrigado ao autor pelo trabalho realizado). Enquanto me aprofundava no estudo do artigo, tive cada vez mais a ideia de tentar escrever meu próprio algoritmo de filtro de determinação de posição, já que, naquele momento, meu nível de conhecimento nessa área havia aumentado significativamente. Por uma questão de interesse, "invente uma bicicleta"! E eu o "inventei". Abaixo eu dou o meu raciocínio.

O algoritmo usa as leituras dos três sensores. Deixe-me lembrá-lo de que a tarefa do algoritmo é calcular a orientação do objeto e compensar a deriva zero do giroscópio, dado o par dado do acelerômetro e magnetômetro. Como uma ferramenta matemática que descreve a posição, um quaternion é usado, porque é conveniente em termos de construção e otimização do algoritmo e requer menos operações matemáticas para calculá-lo, diferentemente das matrizes. O quaternion de rotação no espaço é o seguinte:

$$

$$q = \ left [q_1 \ q_2 \ q_3 \ q_4 \ right]$$

Conhecendo o eixo de rotação descrito pelo vetor normalizado $$$\ vec {v} = \ left [v_x \ v_y \ v_z \ right]$ e ângulo $$$\ varphi$ (de onde eles vêm de cima), você pode calcular o quaternion:

$$

$$q_ {v, \ varphi} = \ left [\ cos \ left (\ frac {\ varphi} {2} \ right) \ \ v_x \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_y \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_z \ sin \ left (\ frac {\ varphi} {2} \ right) \ right] \ quad (*)$$

Então, usando apenas o giroscópio, a cada iteração do ciclo, calcularemos o valor atual do quaternion de acordo com a expressão:

$$

$$q_n ^ G = q_ {n-1} q_ {v, d \ varphi}$$

Aqui $$$q_n ^ G$ - quaternion em um determinado momento. O índice G no topo indica que esse valor se refere à medida em relação às leituras de giroscópio, ou seja, velocidade angular; $$$q_ {n-1}$ - o valor do quaternion no momento anterior; $$$q_ {v, d \ varphi}$ –Alterando a posição em uma etapa de medição, podemos dizer uma mudança discreta de posição por um ângulo $$$d \ varphi$ para $$$dt$ É o período de amostragem expresso pelo quaternião de rotação (*).

O próximo passo no cálculo é encontrar a matriz de rotação com base nos dados de um par de sensores acelerômetro e magnetômetro. Especificamente, consideramos o vetor de gravidade e o vetor de indução do campo magnético da Terra, que, como mencionado acima, são estáticos em relação à Terra e ao NSC associado. Aqui está a tese: conhecendo os valores da gravidade e da indução na base do LSC e do NSC, podemos calcular a matriz de transição (rotação) do NSC para o LSC e o quaternion de rotação no espaço .

Denotar por $$$\ vec {G}$ vetor de gravidade inicial normalizado. Pode ser tomado da seguinte maneira:

$$

$$\ vec {G} = {\ left [0 \ 0 \ 1 \ right]} ^ T$$

Através de $$$\ vec {H}$ denotar o vetor de indução magnética inicial normalizado:

$$

$$\ vec {H} = {\ left [H_x \ H_y \ H_z \ right]} ^ T$$

Um terceiro vetor também é necessário. $$$\ vec {K}$ que está associado a esses dois. É obtido por multiplicação vetorial $$$\ vec {H}$ em $$$\ vec {G}$ :

$$

$$\ vec {K} = {\ left [K_x \ K_y \ K_z \ right]} ^ T = \ vec {H} \ times \ vec {G} = {\ left [H_y \ -H_x \ 0 \ right]} ^ T$$

Agora a matriz é formada $$$M_0$ que caracteriza a posição inicial, ou seja, NSC, já que no momento inicial, o LSC coincide com o NSC. A matriz é obtida a partir dos componentes dos vetores $$$\ vec {H}$ , $$$\ vec {G}$ e $$$\ vec {K}$ :

$$

$$M_0 = \ left [\ vec {H} \ \ vec {G} \ \ vec {K} \ right] = \ left [\ begin {array} {cccc} H_x & 0 & H_y \\ H_y & 0 & -H_x \\ H_z & 1 & 0 \ end { matriz} \ right]$$

Da mesma forma, mas já a cada iteração do loop, uma matriz semelhante é criada $$$M '= \ left [\ vec {h} \ \ vec {g} \ \ vec {k} \ right]$ onde $$$\ vec {h}$ É o vetor de indução magnética normalizado atual, $$$\ vec {g}$ É o vetor de gravidade normalizada atual, $$$\ vec {k} = \ vec {h} \ times \ vec {g}$ . Essa matriz caracteriza a posição do LSC, porque esses vetores são conhecidos no sistema de coordenadas de sensores, que coincide com o LSC. Então, conhecendo as duas matrizes, podemos escrever a seguinte equação:

$$

$$E'M '= E_0M_0$$

Ele liga duas matrizes encontradas em diferentes circunstâncias. Dada uma expressão $$$E '= CE_0$ e que base $$$E_0$ É a matriz de identidade, obtemos:

$$

$$CM '= M_0$$

A partir daqui, expressamos a matriz de transição $$$C$ :

$$

$$C = {\ left (M_0 ^ {- 1} \ right)} ^ TM '^ T$$

O primeiro fator, como você pode entender, é calculado apenas uma vez no início do algoritmo e não requer recontagem no processo. O segundo fator é formado com bastante facilidade e não à força a cada iteração do ciclo.

Depois, quando a matriz de transição é encontrada, nós a transformamos em um quaternion $$$q_n ^ A$ (o algoritmo para converter de uma matriz em um quaternion é algo público e não o darei aqui).

Como resultado, conhecemos dois quaternions encontrados independentemente um do outro. E para combinar os resultados, apliquei um filtro complementar simples com um coeficiente $$$F$ , que é calculado entre 0 e 1:

$$

$$q_n = Fq_n ^ G + \ esquerda (1-F \ direita) q_n ^ A$$

Como resultado, obtemos um quaternion, que contém informações atualizadas sobre a posição no espaço do dispositivo com o módulo SINS.

A bicicleta foi ... O algoritmo funcionou, mas em algumas situações ele se comportou de maneira inadequada, o que em princípio não interferiu, mas não deu motivos para pensar positivamente. Satisfazi meu interesse esportivo e agora você pode recorrer a soluções prontas, melhor. Voltei novamente ao artigo de Sebastian Majwik e decidi usar seu algoritmo, felizmente, que essa pessoa maravilhosa publicou todos os códigos-fonte no site do projeto . O arquivo possuía códigos-fonte em diferentes idiomas, incluindo o idioma do Matlab. Esse fato influenciou minha decisão de abandonar a ideia de fazer todos os cálculos no microcontrolador (principalmente por ser de 8 bits) e escrever o programa já no computador no ambiente Matlab. O microcontrolador é usado apenas para interrogar sensores e enviar dados para um PC (situação semelhante ao do manipulador). Nesse caso, o código principal do programa que sofre alterações e depuração se baseia no ambiente Matlab, o que é muito conveniente no processo.

Bem, a orientação dada pelo quaternion que recebemos. O que vem a seguir de acordo com o plano? E então segue as coordenadas lineares do objeto de acordo com o acelerômetro. Bem, aqui é melhor simplesmente declarar que é impossível determinar as coordenadas usando o acelerômetro com a precisão necessária. Até pelo menos encontre uma mudança de posição que seja adequada! Obviamente, houve tentativas de resolver esse problema, mas em tempo real não foi possível encontrar as coordenadas. Porque Porque a dupla integração discreta das leituras dos sensores ruidosos levou apenas a voar para a estratosfera e a uma velocidade frenética, mas não a um resultado positivo. Portanto, cortei o algoritmo indicado no início do parágrafo até encontrar a orientação e parei por aí.

3. Tudo o resto

Então, cheguei à fase final do design, tendo tocado o suficiente com o manipulador e envolvido o sensor IMU. Enquanto trabalhava nas duas etapas anteriores, eu já tinha uma ideia clara de como tudo funcionaria e por qual algoritmo. Portanto, lidei com essa etapa com rapidez suficiente. Como apenas a orientação da palma da mão é conhecida, trabalhamos diretamente com o corpo de trabalho, o qual é necessário para orientar adequadamente. O RO pode tomar qualquer direção, se não violar a área de trabalho (girar todos os 360 não funciona).

No item sobre o desenvolvimento do manipulador, o vetor do PO foi definido manualmente e, depois disso, foram encontrados os ângulos de rotação dos acionamentos. Portanto, esse vetor deve ser determinado com base na orientação da palma da mão. A orientação pode ser expressa como base $$$E '$ encontrá-lo convertendo o quaternion em uma matriz. A base consiste em vetores de colunas de seus orths; portanto, obtemos três vetores $$$\ vec {x} '$ , $$$\ vec {y} '$ e $$$\ vec {z} '$ . Será conveniente considerar o vetor como orientação $$$\ vec {x} '$ , desde que assumi uma posição inicial do manipulador, quando todos os links e o PO estão localizados no plano XZ do sistema de coordenadas de base, e o PO está horizontal naquele momento, ou seja, vector $$$\ vec {v_0}$ no início, está alinhado com o eixo X do BSK e do NSC (posicionamos a posição inicial do módulo SINS para que o NSC coincida com o BSK do manipulador). Nesse caso, a primeira coluna da matriz $$$E '$ igualar vetor $$$\ vec {v_0}$ . Em seguida, normalizamos ao longo do comprimento do PO e obtemos o vetor necessário em relação ao sistema de coordenadas base do manipulador. A seguir, seguimos a sequência de cálculo das coordenadas generalizadas da página 1.

Vale ressaltar que o manipulador, ao alterar a orientação do RO, é capaz de se mover em dois modos: o primeiro - quando o ponto do flange está estacionário, o segundo - quando o ponto final do pedido está estacionário, mas sua orientação é observada. O segundo modo é mais interessante porque mesmo na ausência de movimento linear, todos os eixos de rotação ainda estão envolvidos para mover o ponto do flange, observando a orientação do PO. No entanto, a transição do primeiro modo para o segundo ocorre com a adição de apenas uma operação de subtração de vetores para encontrar o vetor $$$\ vec {r}$ (ver parágrafo 1)

Todas as operações acima também foram programadas no ambiente Matlab. Em termos gerais, a estrutura do programa é a seguinte:

1. Calibração na inicialização. Definimos o farm inteiro em sua posição original e, sem ousar tocar, calibramos o módulo SINS para uma certa quantidade de dados brutos dele. A calibração é necessária, porque você precisa remover o deslocamento inicial que o filtro produziu (eu não entendi o porquê e funcionou muito bem).
2. O começo do script. Inicializamos todas as bibliotecas e variáveis, definimos a posição inicial do flange ou ponto final do pedido.
3. Início do ciclo. A cada iteração, interrogamos os sensores, encontramos o quaternion, convertemos em uma matriz, que é a base $$$E '$ , é a base na qual o RO está localizado. A primeira coluna é tomada como orientação do pedido e encontramos todas as coordenadas generalizadas usando as considerações matemáticas da Seção 1.
4. Conhecendo as coordenadas generalizadas no último momento e no presente, calculamos a velocidade angular de rotação dos eixos.
5. Enviamos um pacote de dados para o microcontrolador do manipulador.

Evidentemente, ficou desajeitado, mas se você olhar mais de perto, poderá ver um resultado positivo do estudo. Obviamente, este trabalho não pretende ser concluído e exige muito esforço para refinar, mas somente se puder ser usado. Mas ainda não encontrei um aplicativo específico ... Alguém pode me dizer?