
Olá Habr! Neste artigo, falarei sobre a criação de um modelo matemático de um longo pipeline para o programa CAE SimulationX no Modelica. Será uma questão de calcular os processos das ondas (pulsações de pressão, golpe de aríete, etc.) em uma linha hidráulica usando o método das características. Apesar de esse método ser bastante antigo, não há informações suficientes no RuNet sobre sua aplicação na solução de problemas aplicados.
Sob o corte, tentarei explicar por que é necessário levar em conta os processos de ondas nos oleodutos, destacar os problemas que encontrei durante a programação e, no final, farei uma comparação do processo de pulsações de pressão durante a operação de uma bomba de água de alta pressão de três êmbolos em um oleoduto longo simples no modelo e no suporte da URACA em Alemanha.
1. Introdução
Na prática de engenharia, como regra, pouca atenção é dada aos processos de onda nos oleodutos. O exemplo mais famoso, quando os processos de ondas estragam a vida de um engenheiro, é um martelo de água:
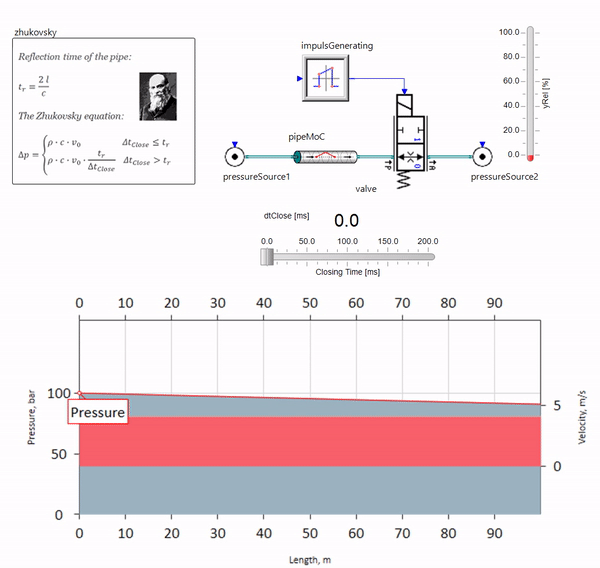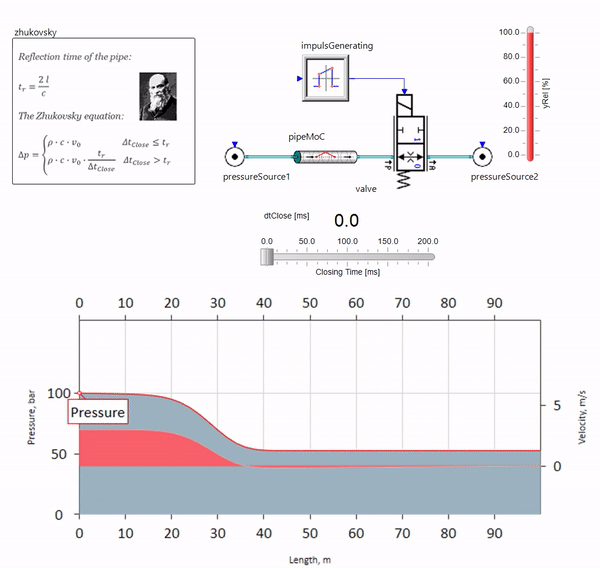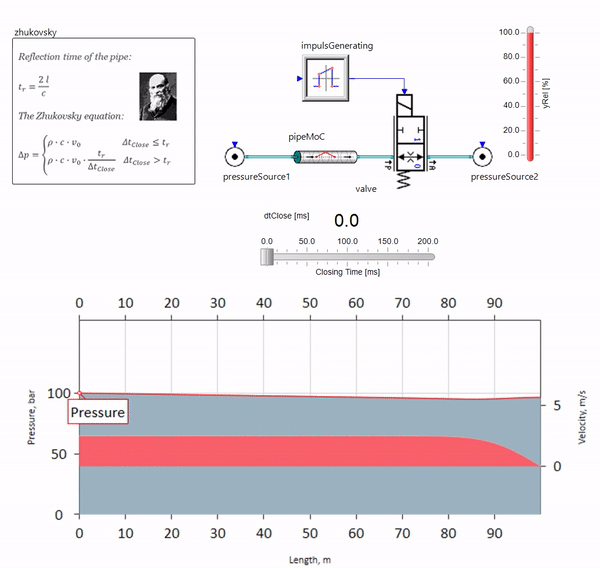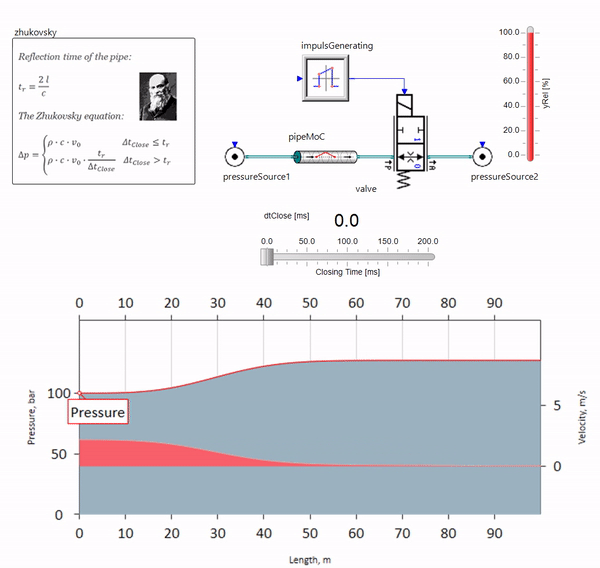
Quando a válvula fecha rapidamente no final da tubulação, a jusante, ocorre uma onda de pressão que se move a montante na velocidade local do som (para a água, aproximadamente 1.500 m / s), é refletida a partir de uma fonte de pressão constante, retorna à válvula e é refletida ela desta vez com um sinal negativo. Este processo é repetido até que toda a energia seja consumida por atrito e até então a válvula e toda a tubulação sejam sujeitas a cargas de choque, cuja amplitude e frequência dependem do comprimento da tubulação e da velocidade inicial do fluxo de fluido.
O hidrobloque com a precisão necessária para resolver problemas práticos foi descrito no final do século 19 por Nikolai Zhukovsky, resolvendo o problema de acidentes no abastecimento de água de Moscou. Desde então, a fórmula para calcular o salto de pressão quando a válvula é fechada rapidamente é chamada de
fórmula de Zhukovsky em todo o mundo:
Na prática, o martelo de água se manifesta, por via de regra, com dutos de cem metros. Em comprimentos abaixo, já é difícil encontrar equipamentos hidráulicos que possam fechar mais rápido do que a onda de pressão passada pela válvula e para trás (a condição para a ocorrência de golpe de aríete). No entanto, mesmo tubulações relativamente curtas ainda podem arruinar a vida dos engenheiros se o sistema tiver uma fonte de pulsações de fluxo (por exemplo, uma bomba volumétrica com um número finito de êmbolos).
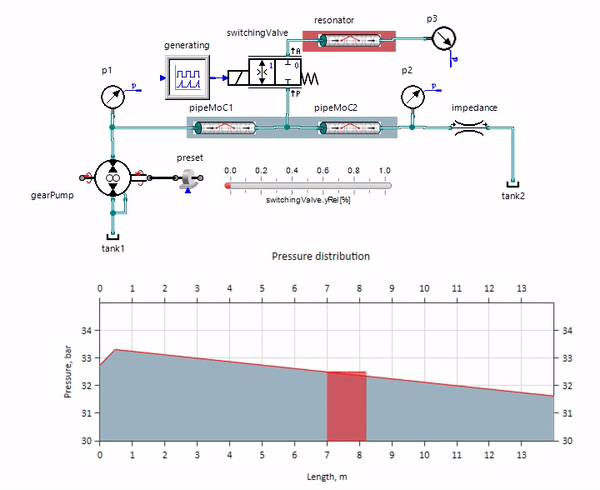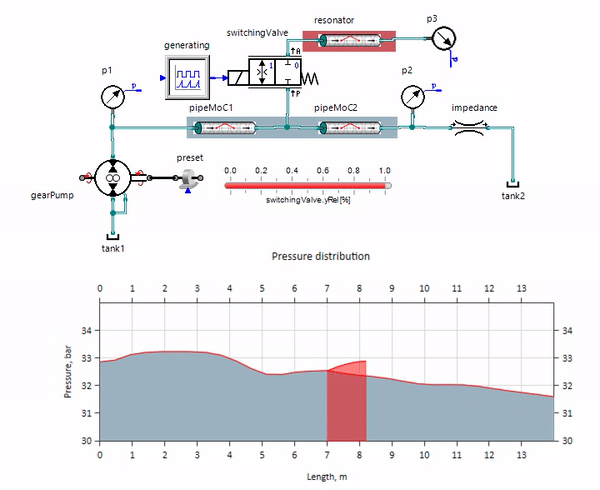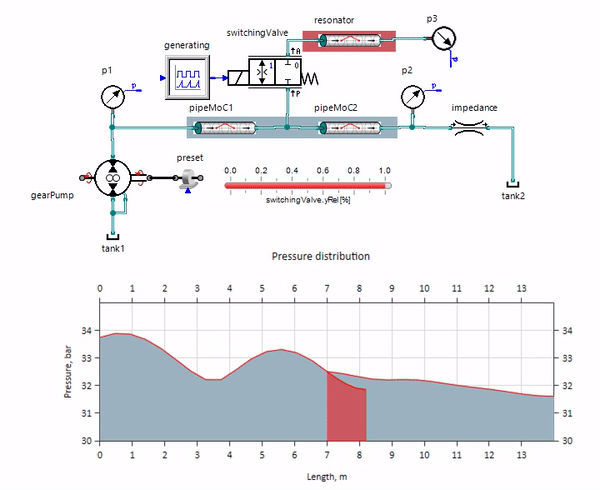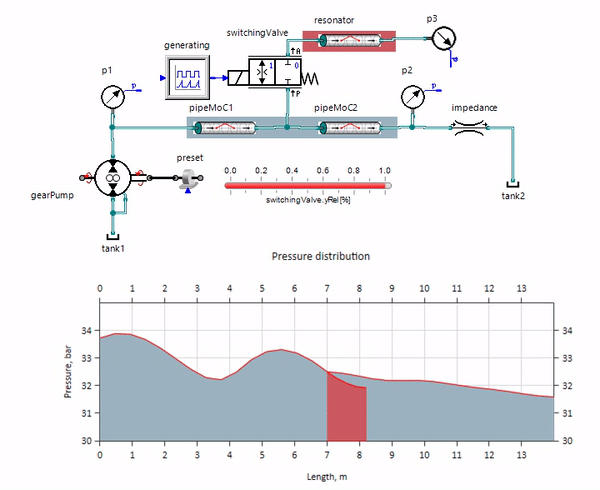
O gif mostra o efeito benéfico de um pedaço de tubulação com pouco mais de um metro de comprimento. Seu comprimento é igual a um quarto do comprimento de onda da pressão; portanto, quando você o conecta ao oleoduto principal, o chamado onda estacionária, que na antifase atinge a fonte das pulsações e as suprime dessa maneira (este é o chamado amortecedor de pulsação de quarto de onda). É claro que, com uma combinação infeliz de circunstâncias, o efeito pode ser o oposto.
Na minha prática, tentei por um longo tempo afastar os processos de onda, porque seu cálculo exigia uma compreensão mais profunda dos métodos numéricos e matan, que ao longo dos meus estudos eu tratei com negligência indulgente. Mas quando um dia vi com meus próprios olhos esse conselho padrão (colocar em todos os lugares um HPP, um acumulador hidráulico, organizar um backup na entrada da bomba) não ajuda a livrar-se das pulsações na bancada nem, além disso, aproximá-los da compreensão dos processos, tive que ir mais fundo no tapete . Especialmente para minha vergonha, meu supervisor de pesquisa já começou a escrever um modelo de pipeline em C ++ para mim.
1. Modelo unidimensional de uma linha hidráulica em parâmetros distribuídos
O principal problema que faz com que os modelos unidimensionais tradicionais descritos por equações diferenciais comuns vão além da zona de conforto é que o oleoduto mais simples, mesmo com as suposições mais atrozes (é completamente preenchido com líquido, tem um comprimento de seção constante, a velocidade do fluido é calculada sobre a seção transversal, os processos de transferência de calor não são considerada) é descrita por equações diferenciais em parâmetros distribuídos (equações de Euler, considerando apenas a força de massa e o atrito no lado direito do segundo avneniya):
onde - densidade - velocidade - pressão - perdas por atrito, - queda de pressão causada pela força gravitacional.I.e. integrar agora você não precisa apenas a tempo
mas também na coordenada espacial
.
No caso de líquidos, você pode simplificar um pouco mais sua vida se reescrever as equações de variáveis conservadoras para variáveis primitivas (velocidade e pressão):
onde - velocidade do som.Agora, se aceitarmos que a velocidade do som é significativamente maior que a velocidade do movimento do fluido
(o que é verdade na ausência de cavitação), as equações se tornarão um pouco mais simples:
Para resolver essas equações, de uma maneira ou de outra, livre-se da diferenciação na coordenada espacial
. Isso pode ser feito de frente se você substituir o diferencial espacial por um esquema de diferenças finitas e, no caso de tempo, apenas acessar o diferencial completo, dizendo que dentro da mesma célula, os parâmetros de estado não dependem da coordenada:
Agora, essas equações podem ser resolvidas como equações diferenciais ordinárias, dividindo o comprimento do tubo em muitos volumes finitos. Isso
é feito , por exemplo, no pacote Simscape, no MATLAB Simulink, e o problema foi resolvido até recentemente no
SimulationX .
Algo assim, é claro, pode ser calculado, mas as flutuações numéricas que surgem neste caso são bastante prejudicadas:
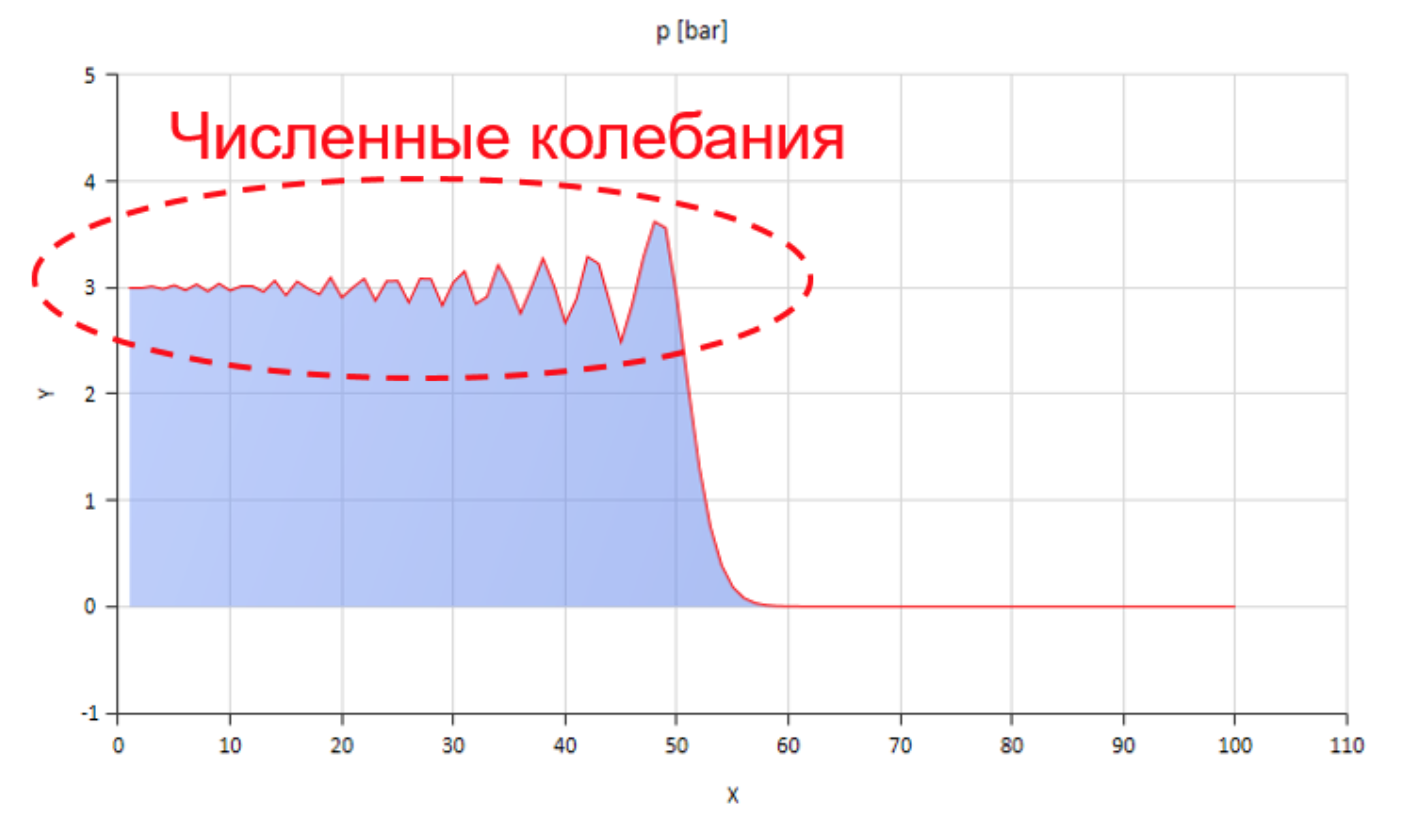 A figura mostra a frente da onda de pressão movendo-se da esquerda para a direita.
A figura mostra a frente da onda de pressão movendo-se da esquerda para a direita.Você pode lidar com essas oscilações, por exemplo, introduzindo difusão numérica, mas a velocidade de propagação da onda é significativamente distorcida. Você pode aumentar o atrito (especialmente ajudando a aumentar seu componente não estacionário), mas o modelo deixa de refletir a essência física.
É melhor usar um método diferente de transformar equações em parâmetros distribuídos em equações diferenciais ordinárias, por exemplo, o método de características.
2. Método de caracterização
A Wikipedia recomenda "Método de características" recomenda:
... encontrar características ao longo das quais a equação diferencial parcial se transforma em uma equação diferencial ordinária. Assim que as equações diferenciais ordinárias são encontradas, elas podem ser resolvidas de acordo com as características e a solução encontrada pode ser transformada em uma solução da equação diferencial parcial original.
É como uma pedra filosofal, mas em vez de transformar metais em ouro, transformamos equações diferenciais parciais em ordinárias e vice-versa. Surge a pergunta: "como aplicar isso na prática?", E de preferência mais eficaz do que os alquimistas medievais ...
Para começar, entenderemos a declaração do problema. No nosso momento inicial, temos algum tipo de distribuição de pressões e velocidades ao longo do comprimento do tubo. Primeiro, dividimos o tubo em um número finito de elementos e atribuímos um valor de pressão a cada face
e velocidade
.
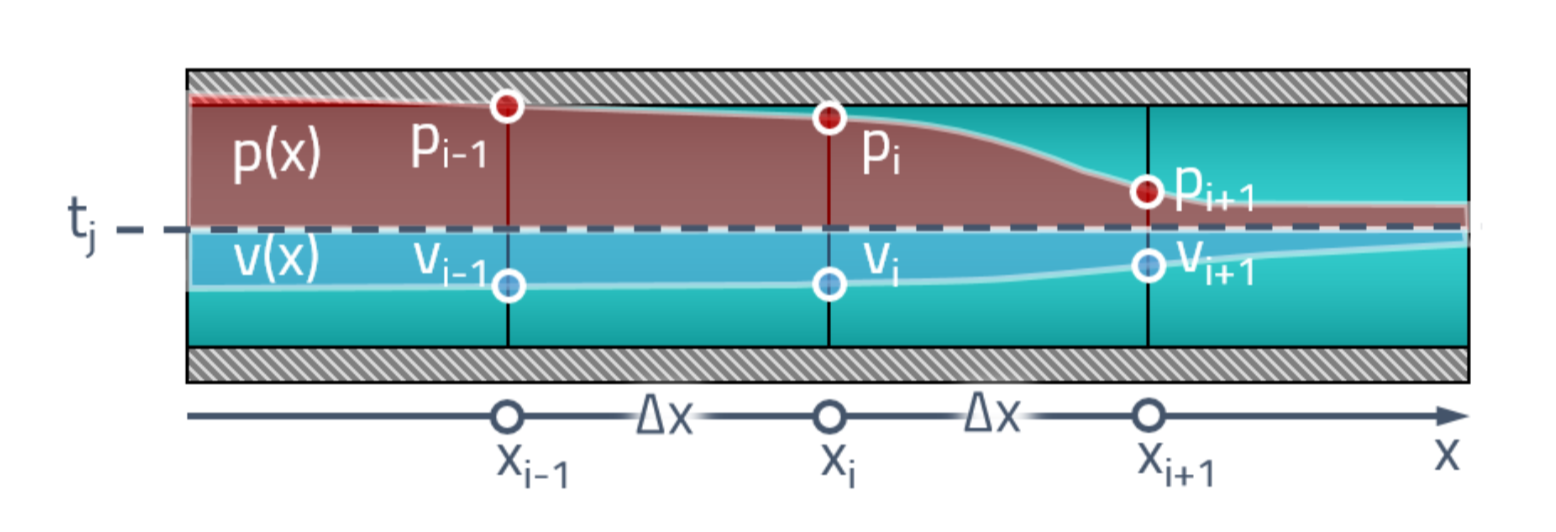
Estamos interessados em saber como os valores nesses pontos mudam ao longo do tempo
. Avance rapidamente para o espaço-tempo e coloque o estado do tubo no futuro acima do estado inicial:

É aqui que as características "mágicas" são úteis! A explicação dos camponeses que trabalham é que todas as mudanças no tubo ocorrem na velocidade do som. Pressão e velocidade no momento atual
dependem da pressão e da velocidade nos pontos do tubo onde a onda sonora estava (seria)
segundos atrás. Isso é ilustrado da seguinte maneira:

Duas linhas simétricas são traçadas a partir de qualquer ponto, cuja inclinação é determinada pela velocidade do som. Essas são as características pelas quais as equações diferenciais parciais se transformam em equações diferenciais ordinárias. Se nomearmos os pontos nos quais as características se cruzam com o estado do tubo no passado como
e
, as equações são escritas da seguinte maneira:
Os valores de pressões e velocidades nesses pontos podem ser obtidos por interpolação linear entre os valores dos parâmetros de estado na grade:

É importante considerar que esses pontos sempre devem estar dentro das células vizinhas! Para isso, o intervalo de tempo deve atender ao critério Courant - Friedrichs - Levy (CFL):
Agora, pelo menos o esquema de diferenças mais simples pode ser aplicado a estas equações:
No sistema resultante de duas equações, duas incógnitas: pressão
e velocidade
. Você pode resolvê-lo numericamente, mas não há nenhum problema específico para obter uma solução analítica. Então, se aceitarmos a constância da velocidade do som, obteremos um esquema de diferenças completamente explícito.
Para consolidar, darei uma animação do método de características:
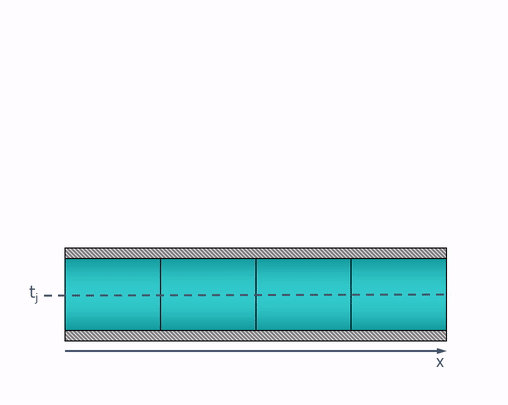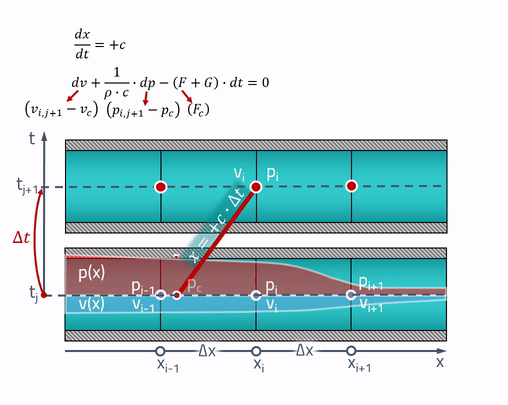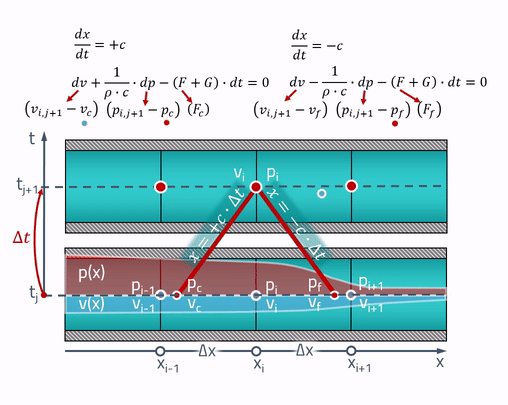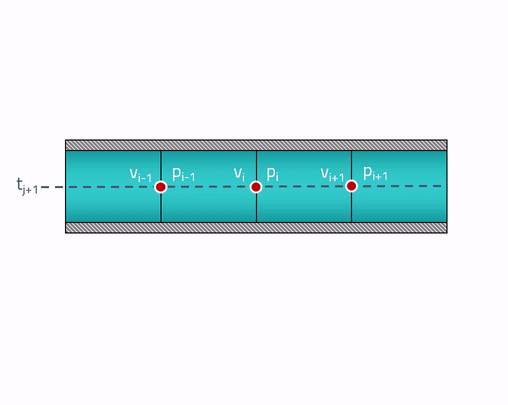
De fato ...... a velocidade do som depende da pressão do fluido. Nesse caso, as características, estritamente falando, não serão mais linhas retas, mas para encontrar a pressão, você precisará conhecer a velocidade do som, que depende dessa pressão. I.e. o circuito já estará implícito.
Ao criar o modelo, aceitei a suposição de que a velocidade do som muda apenas um pouco de um passo para o outro. Para líquidos, isso é verdade no caso de baixo conteúdo de gás e na ausência de cavitação. Para ter certeza do resultado, o modelo é melhor usado com pressões de 10 bar ou mais.
3. Experiência
Eu tive a oportunidade de finalmente lembrar o modelo quando comecei a trabalhar na
ESI ITI GmbH em Dresden. Certa vez, recebi um ingresso no Helpdesk, onde os engenheiros da
URACA reclamaram que não podiam alcançar a convergência com o experimento com o nosso "velho" canal.
Eles fabricam bombas de êmbolo de água de alta pressão, um enorme "Karcher", e gostariam de prever possíveis efeitos ressonantes devido à inclusão processos de onda no pipeline. O problema é que essas bombas, em regra, possuem pouquíssimos êmbolos e operam em baixas velocidades (250-500 rpm):

Devido a isso, e também devido à influência da compressibilidade do líquido, a saída é um fluxo muito desigual:

Lacunas e não linearidades dificultam a linearização e a análise do modelo no domínio da frequência, e os cálculos de CFD para essa tarefa estão disparando de um canhão para pardais. Além disso, eles já tinham modelos no SimulationX, onde levavam em consideração a dinâmica da parte mecânica da bomba, a elasticidade da carcaça e as características do motor elétrico, por isso seria interessante ver como o oleoduto afeta isso.
O layout da bancada de testes é bastante simples:
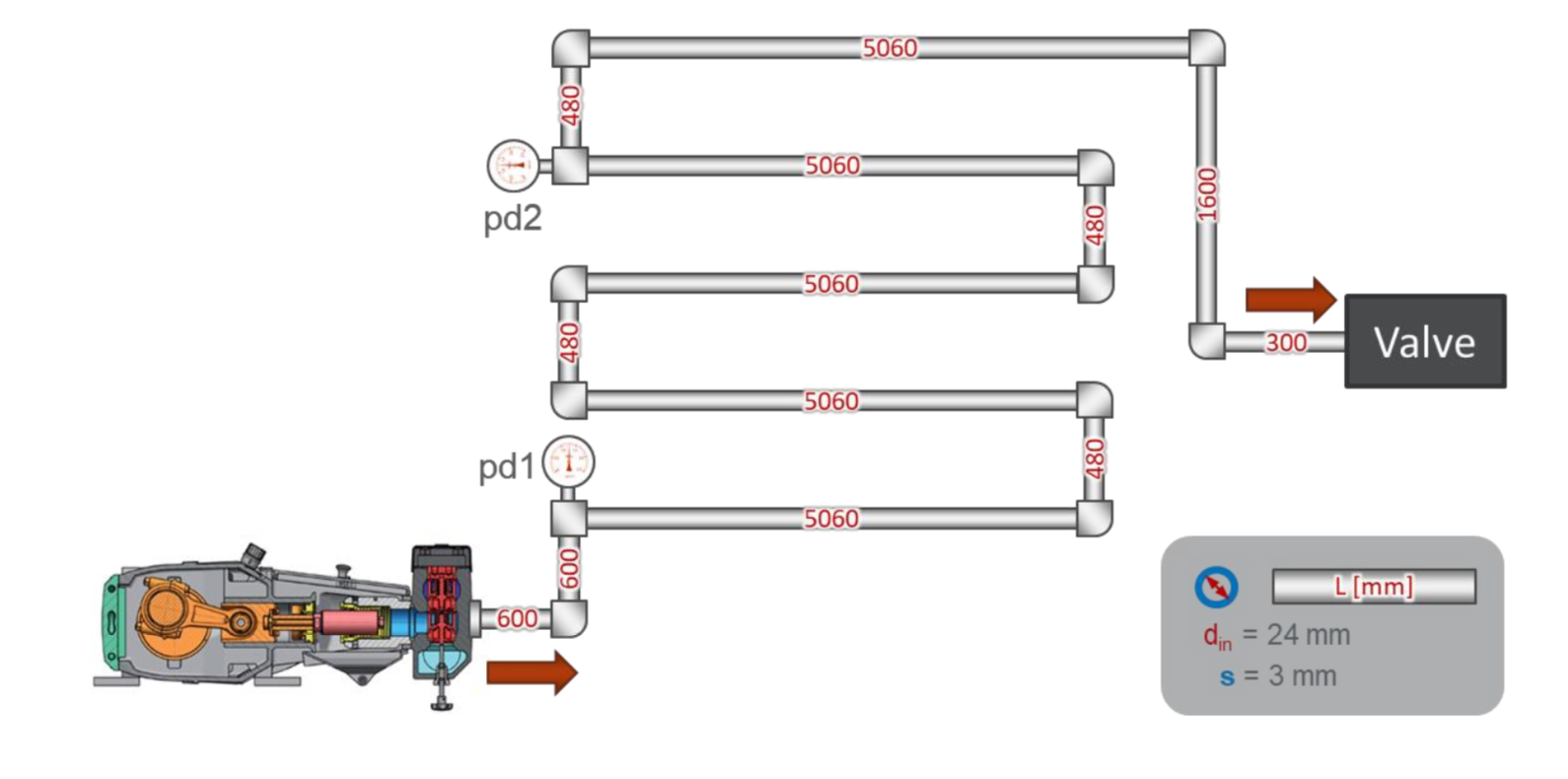
Existe um oleoduto simples com um comprimento total de aproximadamente 30 metros. No início da tubulação, um sensor de pressão pd1 é instalado, a uma distância de 22 metros dele - um sensor de pressão pd2. No final da tubulação, há uma válvula que ajusta a pressão no sistema.
Sugeri testar a versão beta do meu modelo, pois o resultado foi construído no SimulationX:
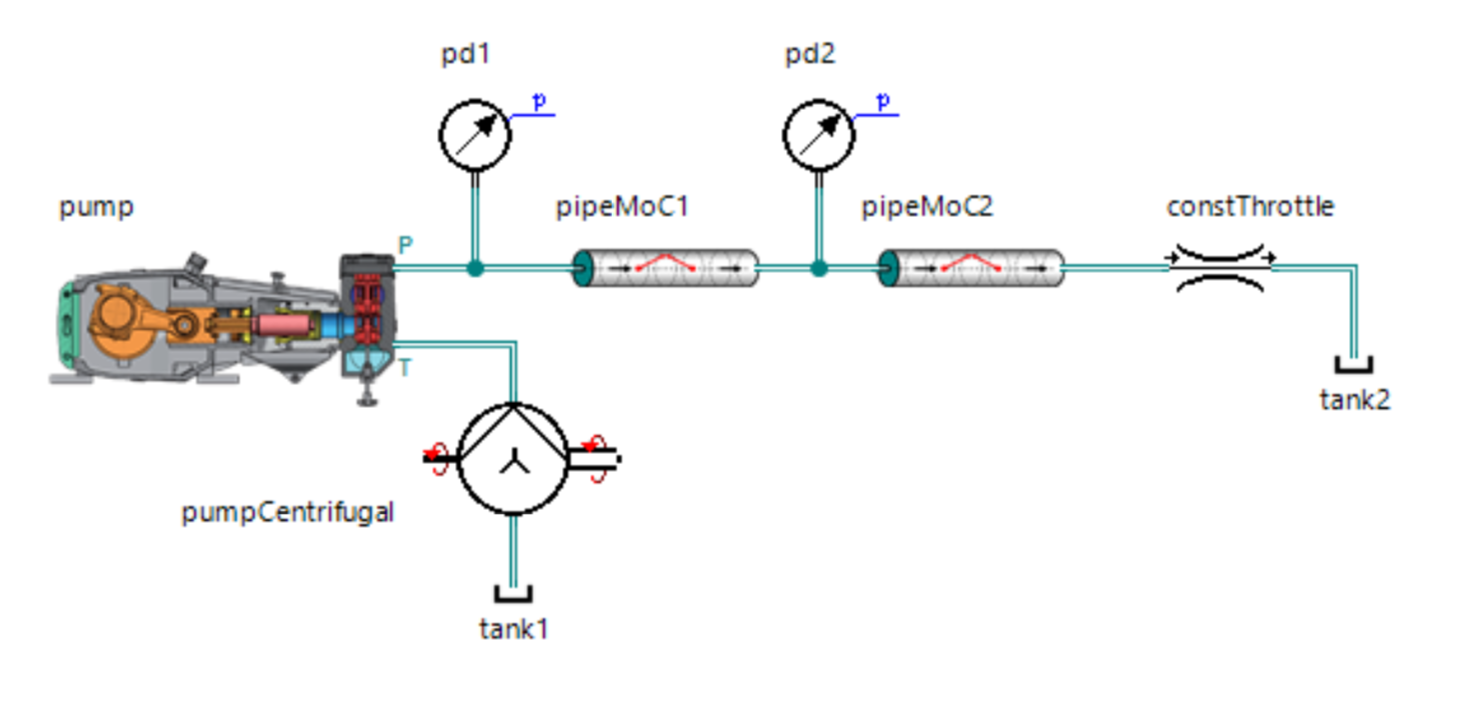
Os resultados até me surpreenderam agradavelmente:
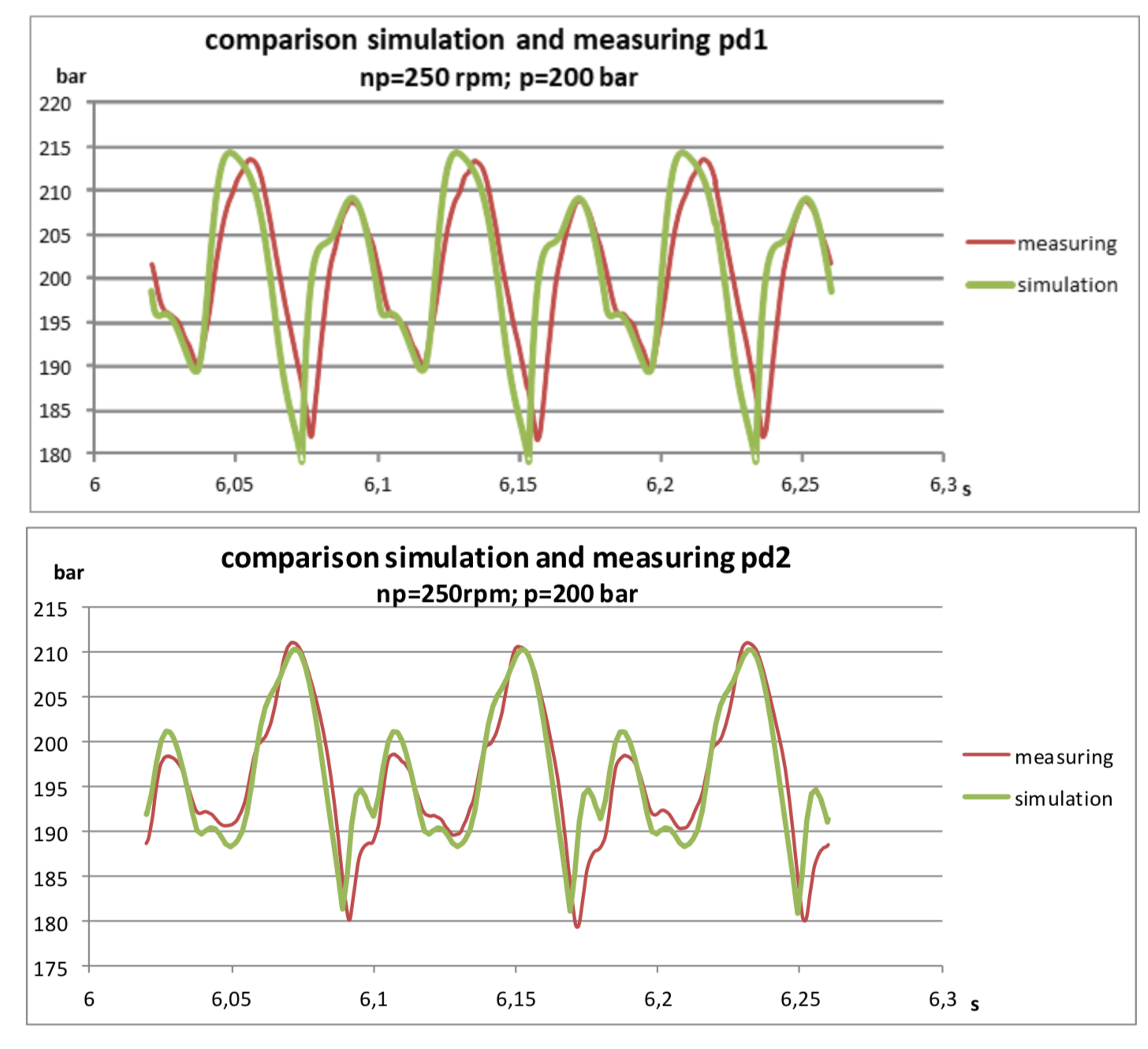
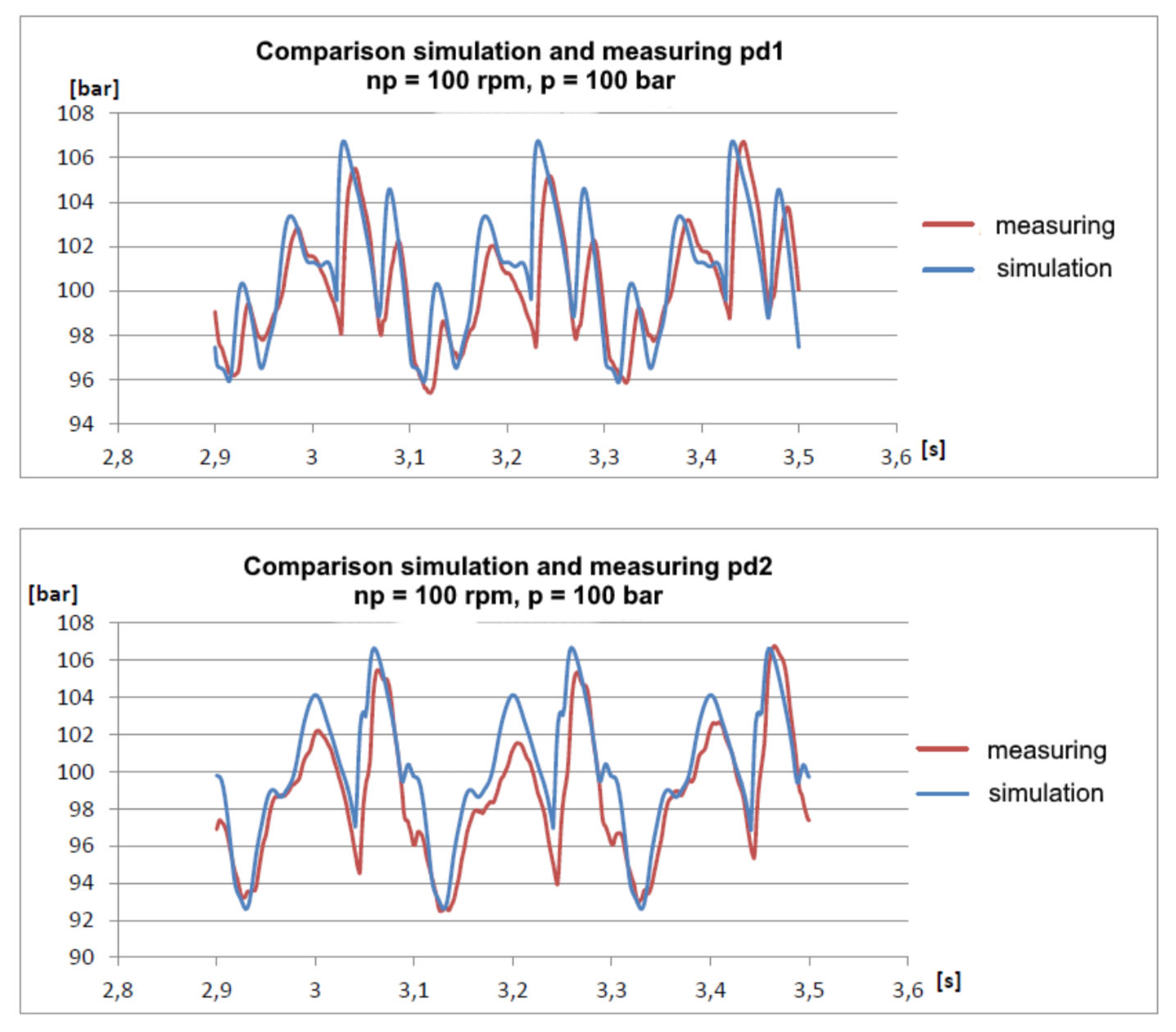
Pode-se observar que o modelo é ligeiramente amortecido, o que é compreensível, desde que não leve em consideração a resistência hidráulica. No entanto, os harmônicos fundamentais são bastante bons por coincidência e possibilitam prever amplitudes de pressão com uma precisão bastante boa.
Essa experiência me permitiu lançar rapidamente um novo modelo da linha hidráulica no lançamento do SimulationX, e mergulhei neste tópico e não percebi como, juntamente com o aluno estagiário, também vi o modelo da linha pneumática, onde tudo era muito mais interessante. Lá, eu tive que usar um método baseado no método Godunov, que, por sua vez, é baseado na solução do problema de Riemann de decaimento de uma descontinuidade arbitrária, bem, sobre isso já de alguma forma outra vez ...
Literatura
- Na literatura doméstica, o método de características para aplicações de engenharia é melhor descrito no livro "Hydromechanics", D. N. Popov, S. S. Panaiotti, M. V. Ryabinin.
- Em sua publicação
Simulação de tubulação pelo método das características para calcular a pulsação de pressão de uma bomba de êmbolo de água de alta pressão“Dr.-Ing. (Rus) Maxim Andreev, Dipl.-Ing. Uwe Grätz e Dipl.-Ing. (FH) Achim Lamparter ”, 11ª Conferência Internacional de Energia Fluida, 11. IFK, 19 a 21 de março de 2018, Aachen, Alemanha, veja o texto em PM
Examinei com mais detalhes os problemas de acoplamento do método de características e do solucionador do ODE. - Quem tem acesso às bibliotecas alemãs, a melhor visão geral dos métodos para resolver equações hiperbólicas aplicadas às linhas hidráulicas que encontrei está contida na seguinte dissertação: Beck, M., Modellierung e Simulation der Wellenbewegung in kavitierenden Hydraulikleitungen, Univ. Stuttgart, Alemanha, 2003.
- Clássicos do gênero de equações hiperbólicas em geral: Randall J. Leveque, Métodos de Volume Finito para Problemas Hiperbólicos, Cambridge University Press, Cambridge, Reino Unido, 2002.