Olá Habr!

Há três anos, no site de Leonid Zhukov, coloquei um link para o curso de Análise de redes Yure Leskovek cs224w e agora o reuniremos com todos em nossa confortável conversa no canal # class_cs224w. Imediatamente após um aquecimento com um curso aberto de aprendizado de máquina que começa em alguns dias.

Pergunta: O que eles lêem lá?
Resposta: Matemática moderna. Mostramos um exemplo de melhoria do processo de recrutamento de TI.

Sob o gato do leitor, há uma história sobre como a matemática discreta levou um gerente de projeto a redes neurais, por que o ERP e os gerentes de produto deveriam ler a revista Bioinformatics, como a tarefa de recomendar conexões apareceu e foi resolvida, quem precisa de gráficos e de onde eles vieram, bem como a opinião de que como parar de ter medo de perguntas sobre árvores nas entrevistas e quanto isso pode custar. Vamos lá!

Nosso plano é o seguinte:

1) O que é cs224w
2) xadrez ou andar
3) Como cheguei a tudo isso?
4) Por que ler a revista de bioinformática
5) O que é incorporação de gráfico e de onde veio
6) Carrinho aleatório em forma de matriz
7) O retorno de um carrinho aleatório e a força dos laços
8) O caminho de um vagabundo aleatório e o topo do vetor
9) Nossos dias são uma caminhada aleatória para todos e todos
10) Como e onde armazenar esses dados e onde obtê-los
11) O que temer
12) Memorando para o jogador

O que é cs224w

O curso da Yure Leskovek Analysis of Networks se destaca na galáxia de produtos educacionais da Faculdade de Ciências da Computação da Universidade de Stanford. A diferença dos outros é que o programa cobre uma ampla gama de questões. É a natureza interdisciplinar que torna a aventura um desafio. O prêmio é a linguagem universal para a descrição de sistemas complexos - teoria dos grafos, que pode ser tratada em dez semanas.

O curso não custa muito, mas abre o programa Mining Massive Data Sets Graduate Certificate , que ainda possui muitos benefícios.

O segundo da aventura é o CS229 Machine Learning, de Andrew Eun, que é desnecessariamente anunciado.

Isso é seguido pelos conjuntos de dados maciços de mineração CS246, Jure Leskoveka, nos quais aqueles que desejam são convidados a descansar no MapReduce e Spark.

Chris Manning termina o banquete CS276 Information Retrieval and Web Search.

Como bônus, o CS246H Mining Massive Data Sets: Hadoop Labs foi projetado especialmente para aqueles que eram poucos. Novamente visitando Yure.

Em geral, eles prometem que aqueles que passaram no programa adquiram habilidades e conhecimentos suficientes para procurar informações na Internet (sem nenhum Google e outros como eles).

Passeio ou damas

Era uma vez, meu líder e mentor, na época - o STO na ucraniana Nestlé, estava me explicando, jovem e ambicioso, tentando conseguir um MBA para se tornar uma estrela, a verdade que experiência e conhecimento estão comprando e vendendo no mercado de trabalho, e não diplomas e resultados dos testes.

A especialização descrita acima pode ser concluída on-line por US $ 18.900 simbólicos.

Em média, uma aventura leva 1-2 anos, mas não mais que 3. Para obter um certificado, você deve concluir todos os cursos com uma classificação de pelo menos B (3,0).

Existe outro caminho.

Todos os materiais dos cursos de Jure Leskovek são publicados de maneira aberta e muito rápida. Portanto, aqueles que desejam podem sofrer a qualquer momento conveniente, coordenando a carga com habilidades. Especialmente talentoso, recomendo experimentar o modo de aventura "This is Stanford, querida!" - passando paralelo ao curso - vídeos das palestras são publicados em alguns dias, literatura adicional está disponível imediatamente, trabalhos de casa e soluções abrem gradualmente.

Nesta temporada, após o final do Curso Aberto de Aprendizado de Máquina em Habré , que é útil para se aquecer, organizaremos uma corrida na classe de canal dedicada # cs_cs224w ods.ai.

É recomendável ter o seguinte conjunto de habilidades:

• Fundamentos de Ciências da Computação em um nível suficiente para escrever programas não triviais.
• Fundamentos da teoria da probabilidade.
• Fundamentos de álgebra linear.

Como cheguei a tudo isso?

Ele viveu por si mesmo, não se incomodou. Projetos de implementação SAP gerenciados. Às vezes - ele atuava como técnico de jogo em sua especialização principal - e o CRM maluco. Você pode dizer que quase não tocou em ninguém. Eu estava envolvido em auto-educação. Em algum momento, decidi me especializar na área de transformação de negócios (ou na realização de mudanças organizacionais). A tarefa de analisar as organizações antes e depois da mudança é uma parte importante deste trabalho. Saber onde e onde mudar ajuda muito. Compreender os relacionamentos entre as pessoas é um fator de sucesso significativo. Ele passou vários anos estudando as metodologias "flexíveis" para pesquisar organizações, mas ainda não estava satisfeito com a pergunta: "Quem escolherá quem: o comandante-chefe do contador principal ou é mais forte que o resto do armazém?" Eu estive pensando por vários anos seguidos. Estou procurando uma maneira de medir com certeza.

2014 foi um momento decisivo, quando abandonei meus sonhos de MBA e escolhi o gerenciamento de estatísticas e informações na nova Universidade de Lisboa (o primeiro e atualmente vivo departamento de telecomunicações da faculdade de aviação e sistemas espaciais da Universidade Politécnica de Kiev) como a segunda mais alta (ouço o tambor) + Departamento de Comunicações das Forças Armadas).

No primeiro semestre da segunda magistratura, ele tentou a análise de redes sociais - uma das aplicações da teoria dos grafos. Foi então que eu aprendi que era algo que, ao que parece, existem algoritmos que resolvem problemas como quem será amigo de alguém contra a implementação de novas tecnologias, mas eu não sabia antes e enxuguei a cabeça, analisando as conexões das pessoas em minha mente - realmente incha com isso. Por acaso, a análise das redes, após os primeiros passos, é uma busca contínua de dados e aprendizado de máquina, com ou sem professor.

No começo, havia clássicos suficientes.

Eu queria mais Para lidar com os casamentos (e reduzir o trabalho de Marinka Zhitnik às suas tarefas), tive que me aprofundar no aprendizado profundo, o que foi muito ajudado pelo curso de Aprendizado Profundo nos dedos . Dada a velocidade com que o grupo Leskovek cria novos conhecimentos, para resolver tarefas gerenciais automaticamente, basta monitorar o trabalho deles.

Por que ler a revista bioinformática

A formação de equipes não é uma tarefa fácil. Quem não deve ser colocado no mesmo barco com um deles é uma das questões prementes. Especialmente quando os rostos são novos. E a área é desconhecida. E para levar a praias distantes, você não precisa de um barco, mas de uma flotilha inteira. E, no caminho, é necessária uma interação próxima, tanto em barcos como entre eles. Dias úteis de implementação da SAP , quando o Cliente precisa fornecer um sistema configurado para suas especificidades a partir de vários módulos, e o plano do projeto consiste em milhares de linhas. Por todo o seu trabalho, ele nunca contratou ninguém - eles sempre emitiram uma equipe. Você é gerente de projeto, tem poderes e se vira. Algo assim. Torcido para fora.

Exemplo de vida:

Eu mesmo não entrevistei, mas aloquei Timlids para isso. E por recursos - demanda de mim. E a integração de novos membros da equipe também é de responsabilidade do gerente de projetos. Acredito que muitos concordam que quanto melhor a lista de candidatos for preparada, mais agradável será o processo para todos os participantes. Vamos considerar essa tarefa em detalhes.

Preguiça natural necessária - encontre uma maneira de automatizar. Encontrei. Eu compartilho.

Um pouco de teoria da administração. A metodologia Adizes é baseada em um princípio básico: organizações, como organismos vivos, têm seu próprio ciclo de vida e demonstram manifestações comportamentais previsíveis e repetitivas durante o crescimento e o envelhecimento. Em cada estágio do desenvolvimento organizacional, a empresa espera um conjunto específico de problemas. Quão bem a gerência da empresa lida com eles, com que êxito faz as alterações necessárias para uma transição saudável de um estágio para outro e determina o sucesso ou o fracasso final dessa organização.

Conheço as idéias de Yitzhak Adizes há cerca de dez anos e, em muitos aspectos, concordo.

As personalidades dos funcionários - como as vitaminas - influenciam o sucesso em determinadas condições. Existem exemplos conhecidos de como líderes de sucesso, saindo de um setor, falharam em outro. Isso acontece pior. Por exemplo, Marissa Mayer, que levantou uma pesquisa no Google, abandonou o Yahoo. Warren Buffett diz que dificilmente conseguiria nascer em Bangladesh. O ambiente e as maneiras de interagir nele são um fator importante.

Seria bom prever complicações antes das experiências em uma vida, certo?

Neste esboço está o próximo estudo de Marinka itnik publicado na revista Bioinformatics. A tarefa de prever efeitos colaterais com o uso combinado de drogas é matematicamente próxima do gerenciamento. Tudo graças à versatilidade da linguagem gráfica. Vamos considerar com mais detalhes.

Rede convolucional dos gráficos da Decagon - uma ferramenta para prever conexões em redes multimodais.

O método consiste na construção de um gráfico multimodal de interações proteína-proteína, interação medicamentosa-proteína e efeitos colaterais de uma combinação de drogas, que são relações droga-droga, em que cada um dos efeitos colaterais é uma margem de um determinado tipo. Decagon prevê um tipo específico de efeito colateral, se houver, que aparece no quadro clínico.

A figura mostra um exemplo de um gráfico de efeitos colaterais obtidos a partir de dados do genoma e da população. No total - 964 tipos diferentes de efeitos colaterais (indicados por costelas do tipo ri, i = 1, ..., 964). Informações adicionais no modelo são apresentadas na forma de vetores das propriedades de proteínas e drogas.

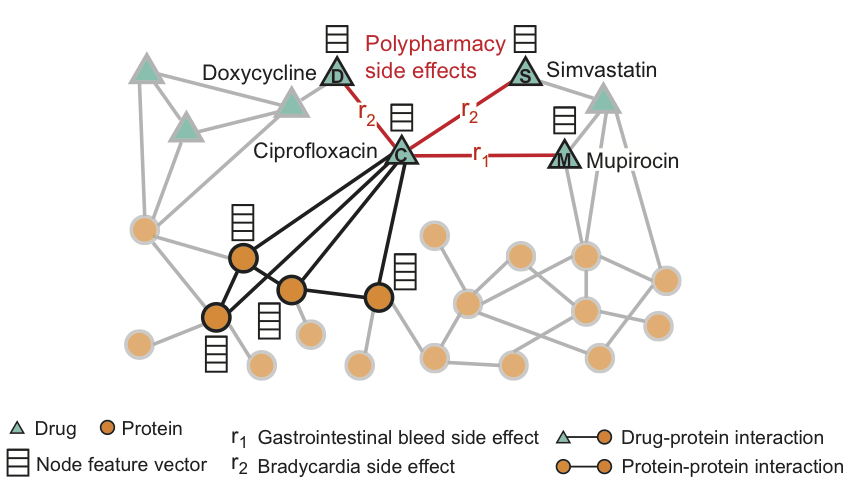
Para a droga Ciprofloxacina (nó C), os vizinhos destacados no gráfico refletem os efeitos em quatro proteínas e três outras drogas. Vimos que a ciprofloxacina (nó C), tomada simultaneamente com doxiciclina (nó D) ou sinvastatina (nó S), aumenta o risco de um efeito colateral de diminuir a freqüência cardíaca (efeito colateral como r2) e uma combinação com mupirocina (M) - aumenta o risco de sangramento do trato gastrointestinal (efeito colateral tipo r1).

Decagon prevê associações entre pares de drogas e efeitos colaterais (mostrados em vermelho) para identificar efeitos colaterais do uso simultâneo, ou seja, efeitos colaterais que não podem ser associados a nenhum dos medicamentos do par separadamente.

Arquitetura de gráfico de redes neurais convolucionais da Decagon:

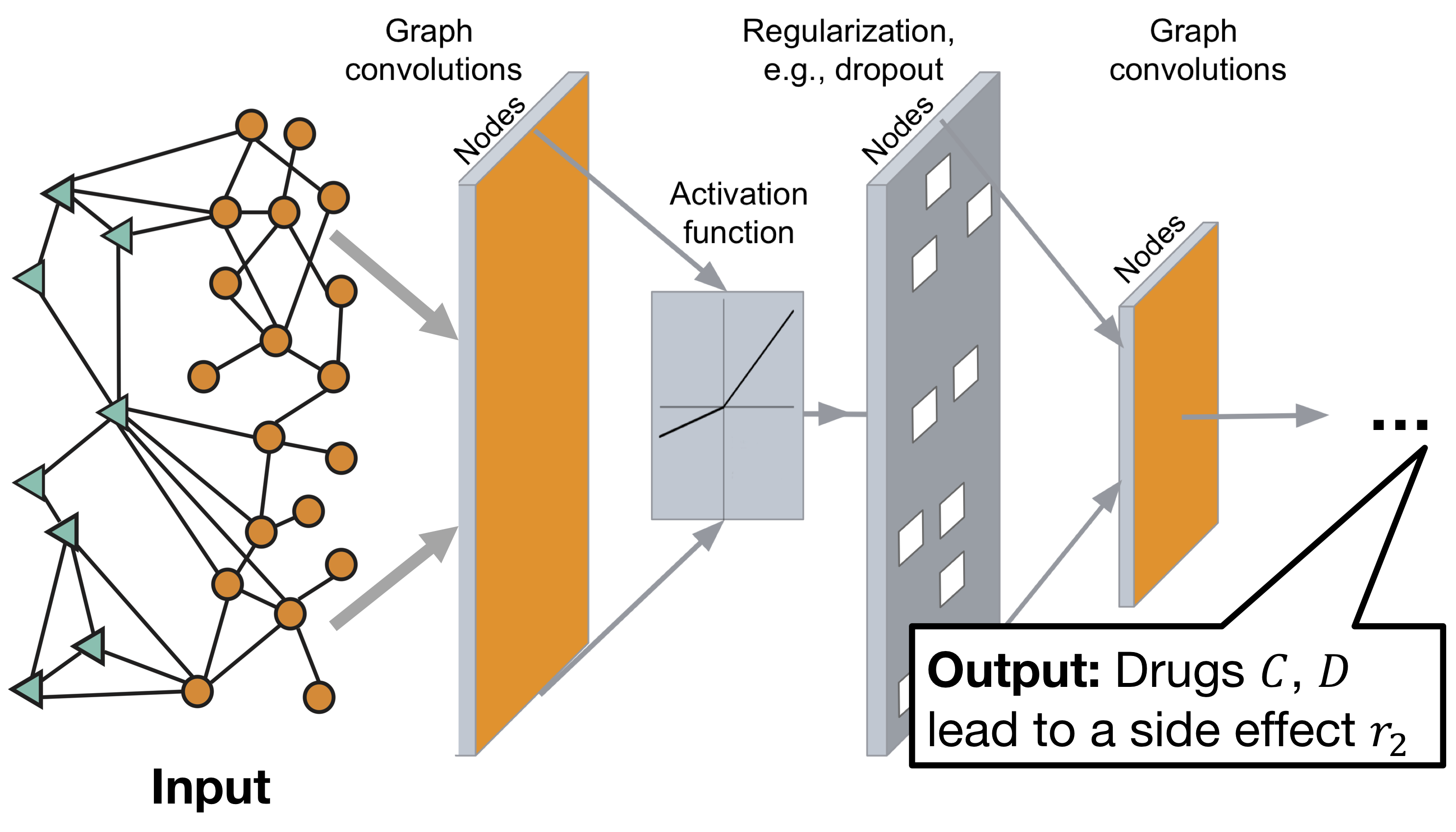
O modelo consiste em duas partes:

Codificador: rede convolucional de grafos (GCN) que recebe um gráfico e incorpora os nós,
Decodificador: um modelo de fatoração de tensor que usa esses embeddings para detectar efeitos colaterais.

Mais informações podem ser encontradas no site do projeto ou abaixo.

Ótimo, mas como vincular isso ao desenvolvimento de equipes?

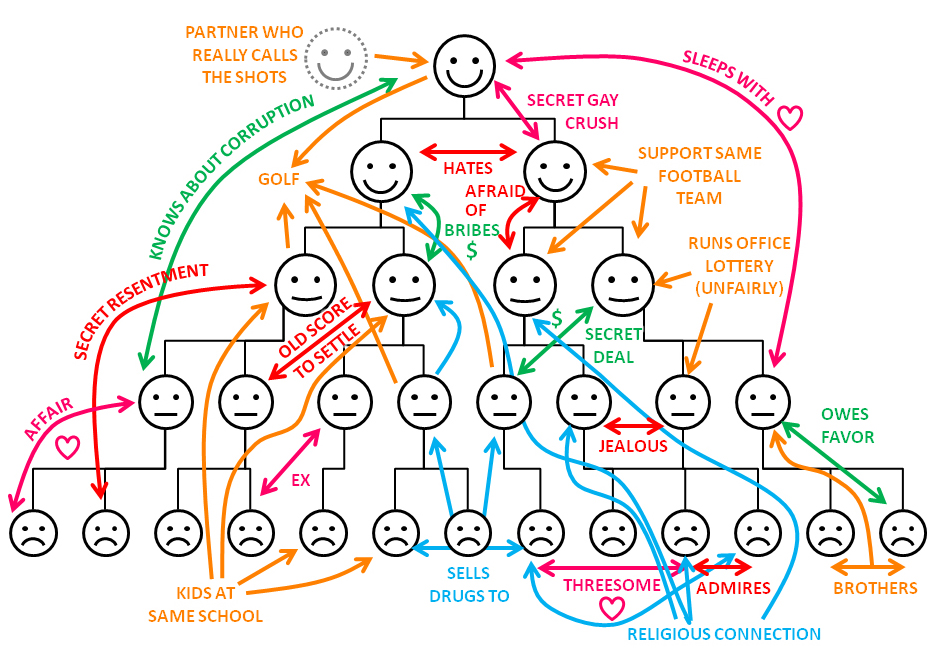
Algo assim .

Aqui, a fim de se sentir confortável no campo de pesquisa, como descrito, e vale a pena cavar a ciência do granito. É verdade que a escavação acontecerá intensamente - a teoria dos grafos está se desenvolvendo ativamente. É por isso que é a ponta de lança do progresso - poucas pessoas se sentem confortáveis ​​lá.

Para entender os detalhes do funcionamento do Decagon, faremos uma excursão pela história.

O que é incorporação de gráfico e de onde ela veio

Por acaso, observei uma mudança no conjunto de métodos avançados para resolver problemas de previsão de conexões em gráficos nos últimos quatro anos. Isso foi divertido. Quase como em um conto de fadas - quanto mais longe, pior. A evolução seguiu o caminho das heurísticas, que determinavam o ambiente para o topo do gráfico, para os carrinhos aleatórios, depois surgiram os métodos espectrais (análise de matriz) e agora as redes neurais.

Formulamos o problema de prever relacionamentos:

Considere um gráfico não direcionado$$ $ inline $ \ begin {align *} G (V, E) \ end {align *} $ inline $ onde
$$$ inline $ \ begin {align *} V \ end {align *} $ inline $ - muitos picos$$ $ inline $ \ begin {align *} v \ end {align *} $ inline $ ,
$$$ inline $ \ begin {align *} E \ end {align *} $ inline $ - muitas costelas$$ $ inline $ \ begin {align *} e (u, v) \ end {align *} $ inline $ conectando os picos$$ $ inline $ \ begin {align *} u \ end {align *} $ inline $ e$$ $ inline $ \ begin {align *} v \ end {align *} $ inline $ .

Definimos o conjunto de todas as arestas possíveis$$ $ inline $ E ^ {\ diamond} $ inline $ seu poder
$$$ inline $ \ begin {align *} | E ^ {\ diamond} | & = \ frac {| V | * (| V | - 1)} {2} \\ \ end {align *} $ inline $ onde
$$$ inline $ \ begin {align *} | V | = n \ end {align *} $ inline $ , É o número de vértices.

Obviamente, muitas arestas inexistentes podem ser expressas como$$ $ inline $ \ begin {align *} \ overline {E} = E ^ {\ diamond} - E \ end {align *} $ inline $ .

Assumimos que no conjunto$$ $ inline $ \ begin {align *} \ overline {E} \ end {align *} $ inline $ há links perdidos ou links que aparecerão no futuro e queremos encontrá-los.

A solução se resume a definir uma função$$ $ inline $ \ begin {align *} D (u, v) \ end {align *} $ inline $ a distância entre os vértices do gráfico, permitindo a estrutura do gráfico$$ $ inline $ \ begin {align *} G (t_0, t_0 ^ \ star) \ end {align *} $ inline $ definido durante um período de tempo$$ $ inline $ \ begin {align *} (t_0, t_0 ^ \ star) \ end {align *} $ inline $ prever a aparência das arestas$$ $ inline $ \ begin {align *} G (t_1, t_1 ^ \ star) \ end {align *} $ inline $ no intervalo$$ $ inline $ \ begin {align *} (t_1, t_1 ^ \ star) \ end {align *} $ inline $ .

Uma das primeiras publicações que propôs a mudança do agrupamento para a tarefa de prever relacionamentos no contexto do estudo da expressão conjunta de genes apareceu na revista (como você pode imaginar) Bioinformática em 2000. Já em 2003, um artigo de John Kleinberg foi publicado com uma visão geral de métodos relevantes para resolver o problema de previsão de conexões em uma rede social. Seu livro " Redes, multidões e mercados: raciocínio sobre um mundo altamente conectado " é um livro recomendado para ser lido durante o curso cs224w, a maioria dos capítulos estão listados na seção de leitura obrigatória.

Um artigo pode ser considerado uma fatia do conhecimento em um campo estreito, como vemos, a princípio, a variedade de métodos era pequena e incluía:

• Métodos baseados em vizinhos de gráfico - e o mais óbvio deles é o número de vizinhos comuns.

Nós damos a definição:

Topo$$ $ inline $ u $ inline $ é um vizinho gráfico para o topo$$ $ inline $ v $ inline $ se costela$$ $ inline $ e (u, v) \ in E $ inline $ .

Nós denotamos$$ $ inline $ \ Gamma (u) $ inline $ muitos vizinhos picos$$ $ inline $ u $ inline $ ,

então a distância entre os picos$$ $ inline $ u $ inline $ e$$ $ inline $ v $ inline $ pode ser escrito como

$$$ inline $ D_ {CN} (u, v) = \ Gama (u) \ cap \ Gama (v) $ inline $ .

Intuitivamente, quanto maior a interseção dos conjuntos de vizinhos de dois picos, mais provável é a conexão entre eles, por exemplo, a maioria dos novos conhecidos ocorre com amigos de amigos.

Heurísticas mais avançadas - coeficiente de Jacquard$$ $ inline $ D_J (u, v) = \ frac {\ Gama (u) \ cap \ Gama (v)} {\ Gama (u) \ xícara \ Gama (v)} $ inline $ (que já tinha cem anos) e recentemente (na época) a distância proposta Adamik / Adar$$ $ inline $ D_ {AA} (u, v) = \ sum_ {x \ in \ Gamma (u) \ cap \ Gamma (v)} \ frac {1} {\ log | \ Gamma (x) |} $ inline $ desenvolva a ideia através de transformações simples.

• Métodos baseados em caminhos ao longo de um gráfico - a idéia é que o caminho mais curto entre dois vértices em um gráfico corresponda à chance de uma conexão entre eles - quanto menor o caminho, maior a chance. Você pode ir além e levar em consideração não apenas o caminho mais curto, mas também todos os outros caminhos possíveis entre pares de picos, por exemplo, pesando os caminhos, como faz a distância de Katz . Já é mencionado o comprimento esperado do caminho de um vagabundo aleatório - o precursor do método de recomendação de amigos do Facebook.

Estime a qualidade da previsão:

• Para cada par de vértices$$ $ inline $ (u, v) $ inline $ toda costela inexistente$$ $ inline $ e (u, v) \ in \ overline {E} $ inline $ calcular a distância$$ $ inline $ D (u, v) $ inline $ no gráfico$$ $ inline $ G (t_0, t_0 ^ \ estrela) $ inline $ .
• Classifique os pares$$ $ inline $ (u, v) $ inline $ distância descendente$$ $ inline $ D (u, v) $ inline $ .
• Leve embora$$ $ inline $ m $ inline $ pares com os valores mais altos é a nossa previsão.
• Vamos ver quantas das arestas previstas apareceram em$$ $ inline $ G (t_1, t_1 ^ \ estrela) $ inline $ .

É importante lembrar que o número de vizinhos comuns e a distância Adamik / Adar são métodos poderosos que especificam o nível básico de qualidade da previsão apenas para a estrutura de links e, se o seu sistema de recomendações mostra um resultado mais fraco, algo está errado.

Geralmente, as combinações de gráficos são uma maneira de representar gráficos de forma compacta para tarefas de aprendizado de máquina usando a função de transformação$$ $ inline $ \ begin {align *} \ phi: G (V, E) \ longmapsto \ mathbb {R} ^ d \ end {align *} $ inline $ .

Examinamos várias dessas funções, a mais eficaz da primeira. Uma lista mais ampla é descrita em um artigo de Kleinberg. Como podemos ver na revisão, mesmo assim eles começaram a aplicar métodos de alto nível, como decomposição de matrizes, agrupamentos preliminares e ferramentas do arsenal da linguística computacional. Quinze anos atrás, tudo estava apenas começando. Os casamentos eram unidimensionais.

Carrinho aleatório em forma de matriz

O próximo marco no caminho para o mesmo gráfico incorporado foi o desenvolvimento de métodos de caminhada aleatória. Inventar e justificar novas fórmulas para calcular a distância, aparentemente, tornou-se uma ruptura. Em algumas aplicações, parece que você só precisa confiar no acaso e confiar nos vagabundos.

Nós damos a definição:

Matriz de adjacência do gráfico$$ $ inline $ g $ inline $ com um número finito de vértices$$ $ inline $ n $ inline $ (numerado de 1 a$$ $ inline $ n $ inline $ ) É uma matriz quadrada$$ $ inline $ a $ inline $ o tamanho$$ $ inline $ n \ vezes n $ inline $ em que o valor do elemento$$ $ inline $ a_ {ij} $ inline $ igual ao peso$$ $ inline $ w_ {ij} $ inline $ costelas$$ $ inline $ e (i, j) $ inline $ .

Nota: aqui nos afastamos intencionalmente dos indicadores de vértice usados ​​anteriormente$$ $ inline $ u, v $ inline $ e usaremos a notação familiar para álgebra linear e, em geral, para trabalhar com matrizes$$ $ inline $ i, j $ inline $ .

Ilustramos os conceitos considerados:

Vamos$$ $ inline $ g $ inline $ - gráfico de quatro vértices$$ $ inline $ \ {A, B, C, D \} $ inline $ conectado por costelas.

Para simplificar as construções, assumimos que as arestas de nosso gráfico são bidirecionais, ou seja,$$ $ inline $ \ para todo e (i, j) \ em E, \ existe e (j, i) \ em E \ terra w_ {ij} = w_ {ji} $ inline $ .

$$$ inline $ e (A, B), w_ {AB} = 1; \\ e (B, C), w_ {BC} = 2; \\ e (A, C), w_ {AC} = 3; \ \ e (B, C), w_ {BC} = 1. $ inline $

Nós representamos os conjuntos de arestas:$$ $ inline $ E $ inline $ - em azul e$$ $ inline $ \ overline {E} $ inline $ - em verde.



$$$ inline $ \ begin {align *} A = \ left [\ begin {matrix} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 \\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {matriz} \ direita] \ end {align *} $ inline $

Escrever um gráfico em forma de matriz abre possibilidades interessantes. Para demonstrá-las, dê uma olhada no trabalho de Sergey Brin e Larry Page e veja como o PageRank, um algoritmo para classificar vértices gráficos, ainda é uma parte importante da pesquisa do Google.

PageRank - criado para pesquisar as melhores páginas da Internet. Uma página é considerada boa se for apreciada (vinculada a) por outras páginas boas. Quanto mais páginas contiverem links para ele, e quanto maior sua classificação, maior o PageRank para uma determinada página.

Considere a interpretação do método usando cadeias de Markov .

Nós damos uma definição: O

grau de um vértice (grau) é o poder de muitos vizinhos:
$$$d_i = |\Gamma(i)|$,

Não estão em graus e fora graus. Para o nosso exemplo, eles são equivalentes.

Construímos uma matriz de adjacência ponderada, guiada pela regra:
$$$\begin{align*}M_{ij} = \left\{ \begin{matrix} \frac{1}{d_j} & \forall i,j \iff i \in \Gamma(j), \\ 0 & \forall i,j \iff i \notin \Gamma(j). \end{matrix} \right.\end{align*}$

$$$\begin{align*}M = \left[ \begin{matrix} 0 & \frac{1}{3} & \frac{1}{2} & 0 \\ \frac{1}{2} &0 & \frac{1}{2} & 1 \\ \frac{1}{2} & \frac{1}{3} & 0 & 0\\ 0 & \frac{1}{3} & 0& 0 \end{matrix} \right]\end{align*}$

, $$$M$1 (.. $$$M$— " "). $$$j$$$$i \in \Gamma(j)$.

$$$r_i$PageRank $$$i$, $$$d_i$. PageRank $$$j$como

$$

$$r_j = \sum_{i \to j}\frac{r_i}{d_i}$$

, $$$i$$$$j$PageRank, (.. PageRank), .

PageRank $$$\begin{align*}r = [r_1, r_2, ..., r_n]^T \end{align*}$— :

$$

$$r = Mr$$

-, ( ). $$$t$$$$i$$$$t+1$$$$j \in \Gamma(i)$, , — .

Nós denotamos $$$p(t)$, $$$i$no tempo $$$t$. $$$p(t)$— , 1.

, $$$M_{ij}$— $$$j$$$$i$, $$$j$e $$$p_j(t)$— , $$$j$$$$t$. , $$$i$

$\$\$display\$\$p\_i(t+1)\; =\; M\_\{i1\}p\_1(t)\; +\; M\_\{i2\}p\_2\; +\; .$. . + M_{in}p_n(t)$$display$$

,

$$

$$p(t + 1) = Mp(t)$$

- , $$$p(t + 1) = p(t)$, $$$p(t)$— . , PageRank $$$r = Mr$. — $$$r$PageRank — !

$$$r$PageRank . , $$$r^{(t0)} = [1/n, 1/n, ..., 1/n]^T$$$$r^{(t+1)} = Mr^{(t)}$$$$t$, , .. $$$||r^{(t+1)} - r^{(t)}||_1 < \epsilon$onde $$$\epsilon$— . ( , $$$||x||_1 = \sum_{k} |x_k|$— $$$L_1$, ). $$$r^{(t+1)}$Page Rank . , 20-30 .

.

"" :

• .. " " — , — , PageRank . . .
• — — PageRank . - . $$$r$.

20 , !

- $$$\beta$, $$$1 - \beta$— . $$$1 - \beta \approx 0.15$, ou seja, - 5-7 . — . PageRank :

$$

$$r_j = \sum_{i \to j}\beta\frac{r_i}{d_i} + (1-\beta)\frac{1}{n}$$

( , )

$$$M$,

$$

$$M^{\star} = \beta M + (1-\beta) [1/n]_{n×n}$$

. $$$r = M^{\star}r$. , , 37-38 14- cs224w 2017 , , Pinterest ( ).

. ?

:

• ;
• ;
• , .

PageRank. , , - , - .

— .

.

, . - ? 2006 .

:

, - $$$G$, - .

$$$i$$$$k$$$$f^{(i)} = [f_1, f_2, ..., f_k]^T$.



, $$$f_1$, , .

, , . - . , — (, ). , IT- , ( ) — .

, , — , , $$$A$e $$$C$— .

, — .

- , Kaggle Hackerrank, , , (, ).

:

$$$S_k(x)$$$$x$$$$k$, $$$G$:

$$$\forall i \in V, i \in S_k(x) \iff f^{(i)}_{k} = x$

:

$$$\begin{align*}M^{p}_{ij} = \left\{ \begin{matrix} \beta M_{ij} + \frac{1-\beta}{|S_k(x)|} & \forall i,j \iff i \in S_k(x), \\ \beta M_{ij} & \forall i,j \iff i \notin S_k(x). \end{matrix} \right.\end{align*}$

$$$\begin{align*} r = M^{p} r \end{align*}$$$$\begin{align*} r \end{align*}$, . $$$\begin{align*} r \end{align*}$PageRank — . , $$$\begin{align*} r \end{align*}$— .

80% Pinterest.

, $$$\begin{align*}|S_k(x)| = 1\end{align*}$, chamado Passeios aleatórios com reinicializações - os carrinhos de bebê voltam e voltam a um pico de interesse para nós. Como resultado, obtemos uma medida de proximidade para cada vértice do gráfico em relação àquele único. E isso resolve o problema de prever conexões melhor do que a distância Adamik / Adar permite.

Adicione mais melhorias:

Lembre-se de que as costelas$$ $ inline $ \ begin {align *} e (i, j) \ in E \ in G \ end {align *} $ inline $ nosso gráfico tem pesos$$ $ inline $ \ begin {align *} w_ {ji} \ end {align *} $ inline $ .

Isso permitirá que você especifique uma matriz ponderada$$ $ inline $ \ begin {align *} M ^ w \ end {align *} $ inline $ probabilidades de transição:

$$$ inline $ \ begin {align *} M ^ {w} _ {ij} = \ left \ {\ begin {matrix} \ frac {w_ {ij}} {\ sum_ {j} w_ {ij}} e \ forall i, j \ iff e (i, j) \ em E, \\ 0 e \ forall i, j \ iff e (i, j) \ não em E. \ end {matrix} \ right. \ end {align *} $ inline $

O vagabundo fará transições, como antes, por acidente, mas não é mais provável!

Um leitor atento já se perguntou como medir esses pesos.

O Facebook ficou intrigado com a mesma coisa em 2011. Era necessário criar um sistema de recomendação para amigos de amigos de amigos, de forma a maximizar a criação de novas conexões. E o primeiro passo foi criar um gráfico ponderado de conexões entre os usuários a partir de informações em seus perfis e histórico de interação (curtidas, mensagens, fotos em comum etc.). De alguma forma, mede o poder da amizade na Internet.

$$$$ display $$ w_ {ij} = f ^ w (i, j) = e ^ {- \ sum_ {z} {\ xi_z x_ {ij} [z]}}, $$ display $$

onde$$ $ inline $ \ begin {align *} x_ {ij} \ end {align *} $ inline $ É o vetor de propriedades dos vértices e das arestas que os conectam, ou seja,$$ $ inline $ \ begin {align *} x_ {ij} = f ^ {(i)} \ cup f ^ {(j)} \ cup f ^ {e (ij)} \ end {align *} $ inline $ e$$ $ inline $ \ begin {align *} \ xi \ end {align *} $ inline $ É o vetor de pesos a ser aprendido com os dados.

Aqui, um leitor treinado reconhecerá um modelo linear e um leitor despreparado pensará no fato de que vale a pena fazer um curso aberto de aprendizado de máquina para lidar com a descida gradiente, com a qual aprenderemos os valores dos pesos em um vetor$$ $ inline $ x_ {ij} $ inline $ - mostrarão como gostos e mensagens afetam as amizades na Internet.

Por que precisamos de tudo isso?

Além do fato de que a abordagem em consideração nos permite prever conexões ainda melhores, podemos aprender as regras para o sucesso da formação de equipes. E descubra o que procurar no futuro.

Lembre-se das condições do nosso exercício. Observamos o desenvolvimento da cooperação (participação conjunta em competições) em um grupo de dataaentists condicionais no intervalo$$ $ inline $ \ begin {align *} (t_0, t_0 ^ \ star) \ end {align *} $ inline $ (por exemplo, um mês) e queremos prever a formação de equipes no intervalo$$ $ inline $ \ begin {align *} (t_1, t_1 ^ \ star) \ end {align *} $ inline $ (outro mês). Além de participar de competições, rastreamos a comunicação em fóruns, gostos de kernels e o que mais você gosta. Todas as informações coletadas são armazenadas em uma matriz$$ $ inline $ X ^ {\ estrela} \ in \ mathbb {R} ^ {(2k + l) \ times | E |} $ inline $ (suas colunas são vetores$$ $ inline $ x_ {ij} $ inline $ ,$$ $ inline $ k, l $ inline $ - dimensões dos vetores de propriedades de vértices e arestas$$ $ inline $ f ^ {(i)}, f ^ {e (ij)} $ inline $ , respectivamente) e o gráfico$$ $ inline $ \ begin {align *} G \ end {align *} $ inline $ por dois intervalos de tempo.

Vamos preparar os dados para o aprendizado de máquina.

Para cada vértice$$ $ inline $ \ begin {align *} i \ end {align *} $ inline $ :

1) defina muitos amigos de amigos:

$$$$ display $$ \ Gamma ^ {fof} (i) = \ bigcup_ {j \ in \ Gamma (i)} \ Gamma (j) - \ Gamma (i) $$ display $$

2) e construir sub-gráficos$$ $ inline $ \ begin {align *} G ^ {fof} (i) \ end {align *} $ inline $ conexões com amigos e amigos de amigos,$$ $ inline $ \ begin {align *} \ for all e (x, y) \ in E, e (x, y) \ in G ^ {fof} (i) \ iff x, y \ in \ Gamma ^ {fof} (i) \ cup \ Gamma (i) \ end {align *} $ inline $

3) selecione o conjunto de vértices,$$ $ inline $ \ begin {align *} D_i: \ {d_1, ..., d_k \} \ end {align *} $ inline $ com quem formamos conexões são nossos exemplos positivos de aprendizado,

4) todas as conexões não aleatórias do conjunto$$ $ inline $ \ begin {align *} \ overline {D_i} = \ Gamma ^ {fof} (i) - D_i \ end {align *} $ inline $ - Estes são nossos exemplos negativos de treinamento.

Nossa tarefa é selecionar esse vetor de pesos$$ $ inline $ \ begin {align *} \ xi \ end {align *} $ inline $ em que exemplos positivos do conjunto$$ $ inline $ \ begin {align *} D_i \ end {align *} $ inline $ obterá um valor maior de PageRank personalizado em relação a$$ $ inline $ \ begin {align *} i \ end {align *} $ inline $ que exemplos negativos.

Para isso, definimos a função de perda, que minimizaremos:

$$$$ display $$ L = \ sum_ {i} \ sum_ {d \ in D_i, \ overline {d} \ in \ overline {D_i}} h (r _ {\ overline {d}} - r_ {d}) + \ lambda || \ xi || ^ 2, $$ display $$

onde$$ $ inline $ h (x) = 0 \ iff x <0; h (x) = x ^ 2 \ iff x \ geqslant 0; $ inline $ - penalidade por violação dos termos,$$ $ inline $ \ lambda $ inline $ - poder$$ $ inline $ L_2 $ inline $ regularização de pesos$$ $ inline $ \ xi $ inline $ ,$$ $ inline $ r $ inline $ É um vetor com soluções da equação$$ $ inline $ r = M ^ wr $ inline $ a respeito$$ $ inline $ r $ inline $ para um sub-gráfico de amigos de amigos de um único topo$$ $ inline $ i $ inline $ .

Um detalhe engraçado - o gradiente dessa função é calculado da mesma maneira que o PageRank, pelo método de potência. Os detalhes estão na 17ª palestra da edição de 2014, slides 9 a 27.

Era assim que era a ponta de lança do progresso no momento em que conheci o curso cs224w.

Caminho de carrinho aleatório e top em vetor

E então veio o triunfo da preguiça!

Sabe-se que a teoria dos gráficos foi inventada por Leonard Euler quando ele estava entediado em resolver o problema insolúvel das pontes que agora estão em Kaliningrado. Em vez de secar a cabeça por nada, ele inventou um aparato matemático que lhe permite provar a impossibilidade fundamental de resolver o enigma.

Nas melhores tradições das ciências computacionais, também seremos preguiçosos e nos perguntamos a tarefa de encontrar uma função que nos permita nos afastar das representações unidimensionais dos nós e ir para os vetores de propriedades multidimensionais.

Aqui nos familiarizamos com os incorporamentos gráficos no sentido moderno do termo.

Formalmente, queremos:

1) Defina um codificador (uma função de conformidade da ENC que define uma transformação de nó$$ $ inline $ u $ inline $ em vetor$$ $ inline $ z_u $ inline $ );
2) Determinar a função de similaridade dos nós (uma medida de proximidade no gráfico, que aplicaremos à entrada do codificador);
3) Otimize os parâmetros do codificador para que:

$$$$ exibição $$ similaridade (u, v) \ aprox z_ {v} ^ {T} z_v $$ exibição $$

Nós nos esforçamos para garantir que os vértices espaçados no gráfico recebam uma representação próxima no mapeamento vetorial. Em outras palavras, para que o ângulo entre os dois vetores obtidos seja mínimo.

Ótimo, mas como determinar isso, essa proximidade no gráfico?

Por exemplo, assumimos que o peso da nervura é uma boa medida de proximidade e pode ser considerado aproximadamente igual ao produto escalar para incorporação de dois nós. A função de perda para este caso terá o seguinte formato:

$$$$ exibir $$ L = \ soma _ {(u, v) \ em V \ vezes V} || z_ {u} ^ {T} z_v - A_ {u, v} || ^ 2, $$ display $$

resta encontrar (por exemplo, descida gradiente) a matriz$$ $ inline $ Z \ in \ mathbb {R} ^ {d \ times | V |} $ inline $ o que minimiza$$ $ inline $ L $ inline $ .

Uma abordagem alternativa é determinar o ambiente.$$ $ inline $ N (v) $ inline $ pois a cúpula é mais larga que muitos vizinhos.

Isso nos ajudará a percorrer o gráfico. O primeiro projeto a usar essa abordagem é o DeepWalk . A essência do método é que iniciaremos uma caminhada para percorrer o gráfico aleatoriamente a partir de cada vértice$$ $ inline $ v $ inline $ , e alimentar sequências curtas de picos fixos visitados durante sua caminhada no word2vec.

A intuição aqui é que a distribuição de probabilidade de visitar os vértices do gráfico - uma lei da potência - é muito semelhante à distribuição de probabilidade do aparecimento de palavras em línguas humanas. E como o word2vec funciona para palavras, então para gráficos pode. Tentamos - funcionou!

No DeepWalk, um vagabundo implementa um processo de Markov de primeira ordem - de cada vértice vamos para o vizinho, de acordo com as probabilidades de uma matriz de adjacência ponderada$$ $ inline $ M $ inline $ (ou seus derivados, como$$ $ inline $ M ^ w $ inline $ ) Onde chegamos ao topo não afeta a escolha do próximo passo.

Para implementar a caminhada, você precisará de um gerador de números pseudo-aleatórios e um pouco de álgebra . É hora de usar o bloco para cotações para a finalidade a que se destina.

“Quem concorda com os métodos aritméticos de geração, é claro, é pecador. Como foi mostrado repetidamente, não existe um número aleatório - existem apenas métodos para criar esses números, e um procedimento aritmético rigoroso, é claro, não é esse método ... Lidamos apenas com receitas para criar números ... "

- John von Neumann

Resta aconselhar aqueles que se esforçam por uma vida justa a encontrar o álbum "Black and White Noise" à venda - em 1995, George Marsaglia escreveu no CD uma matriz de bytes recebidos pela digitalização do ruído do amplificador durante a reprodução do rap e o nomeou de acordo.

O desenvolvimento do método é o node2vec , no qual o processo de Markov de segunda ordem é implementado - examinamos de onde veio e isso afeta a probabilidade de escolher a direção do próximo passo. Vamos ver como isso funciona.

Digamos que começamos um vagabundo andando pelo gráfico a partir do topo$$ $ inline $ u $ inline $ adjacente ao topo$$ $ inline $ s_1 $ inline $ tops$$ $ inline $ s_2 $ inline $ e$$ $ inline $ w $ inline $ - em duas etapas, e$$ $ inline $ s_3 $ inline $ - em três. Após cada etapa, podemos executar uma das três ações possíveis: 1) retornar mais perto$$ $ inline $ u $ inline $ ; 2) explore os picos à mesma distância de$$ $ inline $ u $ inline $ , como aquele em que estamos agora; 3) afaste-se de$$ $ inline $ u $ inline $ .

Essa estratégia é implementada usando dois parâmetros:
$$$ inline $ p $ inline $ - define a probabilidade de retornar ao vértice anterior;
$$$ inline $ q $ inline $ - define o equilíbrio entre a pesquisa em largura e a pesquisa em profundidade.

Esses parâmetros determinam as probabilidades de transição não normalizadas da seguinte maneira:

Digamos que estamos no topo$$ $ inline $ w $ inline $ e entrou nele de cima$$ $ inline $ s_1 $ inline $ . Para costela$$ $ inline $ e (w, s_1) $ inline $ atribuiremos peso (probabilidade não normalizada)$$ $ inline $ 1 / p $ inline $ . Para costela$$ $ inline $ e (w, s_2) $ inline $ -$$ $ inline $ 1 $ inline $ (como em todas as outras arestas que levam a vértices equidistantes de$$ $ inline $ u $ inline $ ) Por se afastar$$ $ inline $ u $ inline $ costelas$$ $ inline $ e (w, s_3) $ inline $ -$$ $ inline $ 1 / q $ inline $ .

Em seguida, normalizamos as probabilidades (para que a soma seja igual a 1) e damos o próximo passo.

Estamos interessados ​​na sequência de picos visitados - nós o enviaremos para o word2vec ( este artigo o ajudará a lidar com isso, ou a aula 8 do curso Deep Learning nos dedos ). A seleção de estratégias para o vagabundo, ideal para resolver problemas específicos, é uma área de pesquisa ativa. Por exemplo, o node2vec, que analisamos, é um defensor da classificação dos picos (por exemplo, determinar a toxicidade dos medicamentos ou o sexo / idade / raça de um membro de uma rede social).

Vamos otimizar a probabilidade do aparecimento de picos no caminho do vagabundo, a função de perda:

$$$$ display $$ L = \ sum_ {u \ in V} \ sum_ {v \ in N_ {R} (u)} -log (P (v | z_u)) $$ display $$

em sua forma explícita, uma carga computacional bastante cara

$$$$ display $$ L = \ sum_ {u \ in V} \ sum_ {v \ in N_ {R} (u)} -log (\ frac {e ^ {z_ {u} ^ {T} z_v}} { \ sum_ {n \ no V} e ^ {z_ {u} ^ {T} z_n}}), $$ display $$

que, por acaso, é resolvido por amostragem negativa , porque

$$$$ display $$ log (\ frac {e ^ {z_ {u} ^ {T} z_v}} {\ sum_ {n \ in V} e ^ {z_ {u} ^ {T} z_n}}) \ aprox log (\ sigma (z_ {u} ^ {T} z_v)) - \ sum_ {i = 1} ^ {k} log (\ sigma (z_ {u} ^ {T} z_ {n_i})), \\ onde \, \, \, n_i \ sim P_V, \ sigma (x) = \ frac {1} {1 + e ^ {- x}}. $$ display $$

Então, descobrimos como obter uma representação vetorial dos vértices. A coisa é o chapéu!

Como preparar casamentos para costelas:

Precisamos definir um operador que permita qualquer par de vértices$$ $ inline $ u $ inline $ e$$ $ inline $ v $ inline $ construir representação vetorial$$ $ inline $ z _ {(u, v)} = g (z_u, z_v) $ inline $ , independentemente de estarem conectados no gráfico. Esse operador pode ser:

a) média aritmética:$$ $ inline $ [z_u \ oplus z_v] _i = \ frac {z_u (i) + z_v (i)} {2} $ inline $ ;
b) o trabalho de Hadamard:$$ $ inline $ [z_u \ odot z_v] _i = z_u (i) * z_v (i) $ inline $ ;
c) norma L1 ponderada:$$ $ inline $ || z_u - z_v || _ {\ overline {1} i} = | z_u (i) - z_v (i) | $ inline $ ;
d) taxa ponderada de L2:$$ $ inline $ || z_u - z_v || _ {\ overline {2} i} = | z_u (i) - z_v (i) | ^ 2 $ inline $ .

Em experimentos, o trabalho de Hadamard se comporta de maneira mais constante.

Por precaução, lembre-se do Teorema do Almoço Gratuito:

Nenhum algoritmo é universal - vale a pena conferir vários métodos.

O desenvolvimento do node2vec é o projeto OhmNet , que permite combinar vários gráficos em uma hierarquia e criar incorporamentos de vértices para diferentes níveis da hierarquia. Foi originalmente desenvolvido para modelar as ligações entre proteínas em diferentes órgãos (e elas se comportam de maneira diferente dependendo da localização).

Um leitor astuto verá semelhanças com a estrutura organizacional e os processos de negócios.

E nós - retornaremos a um exemplo do campo do recrutamento de TI - a seleção das pessoas mais adequadas para a equipe já existente. Antes, consideramos gráficos unimodais de relacionamentos de dataaentists condicionais obtidos a partir do histórico de interação (no gráfico unimodal do vértice e da conexão - do mesmo tipo). Na realidade, o número de círculos sociais nos quais um indivíduo pode ser incluído é mais de um.

Suponha que, além do histórico de participação conjunta em competições, também tenhamos coletado informações sobre como os datacenters são comunicados em nosso bate-papo acolhedor . Agora já temos dois gráficos de conexões, e o OhmNet é perfeito para resolver o problema de criar incorporações de várias estruturas.

Agora - sobre as deficiências de métodos baseados em codificadores rasos - no word2vec, existe apenas uma camada oculta, cujos pesos codificam a codificação. Na saída, obtemos uma tabela de correspondência vetor-vértice. Todas essas abordagens têm as seguintes limitações:

• Cada vértice é codificado por um vetor exclusivo e o modelo não implica compartilhar parâmetros;
• Só podemos codificar os vértices que o modelo viu durante o treinamento - não podemos fazer nada pelos novos vértices (exceto como treinar o codificador novamente);
• Os vetores de propriedades de vértices não são levados em consideração de forma alguma.

As redes convolucionais do gráfico são livres das deficiências indicadas. Chegamos ao Decagon!

Nossos dias são uma caminhada aleatória para todos e todos

Sobre vagabundos, tive a sorte de escrever meu primeiro mestrado e defendê-lo em 2003, mas com treinamento profundo eu tive que seguir o caminho clássico para descobrir o que estava por trás. E é engraçado lá.

Primeiro, vamos ver por que os métodos padrão de aprendizado profundo - não se encaixam nos gráficos.

Contagens não são gatos para você!

O moderno conjunto de ferramentas de aprendizado profundo (redes multicamadas, convolucionais e recorrentes) é otimizado para solucionar problemas em dados bastante simples - sequências e treliças. Um gráfico é uma estrutura mais complicada. Um dos problemas que nos impedirá de pegar a matriz de adjacência e enviá-la para a rede neural é o isomorfismo .

Na nossa coluna de brinquedos$$ $ inline $ g $ inline $ constituído por vértices$$ $ inline $ \ {A, B, C, D \} $ inline $ , para construir uma matriz de adjacência$$ $ inline $ a $ inline $ , sugerimos numeração de ponta a ponta$$ $ inline $ \ {1,2,3,4 \} $ inline $ . É fácil ver que podemos numerar os vértices de maneira diferente, por exemplo$$ $ inline $ \ {1,3,2,4 \} $ inline $ ou$$ $ inline $ \ {4,1,3,2 \} $ inline $ - cada vez que recebe uma nova matriz de adjacência do mesmo gráfico.

$$$ inline $ \ begin {align *} A = \ left [\ begin {matrix} 0 & 1 & 3 & 0 \\ 1 & 0 & 2 & 1 \\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \ end {matriz} \ direita], \, A ^ {\ {1,3,2,4 \}} = \ left [\ begin {matrix} 0 & 3 & 1 & 0 \\ 3 & 0 & 2 & 0 \\ 1 & 2 & 0 & 1 \\ 0 & 0 & 1 & 0 \ end {matrix} \ right], \, A ^ {\ {4,1,3,2 \}} = \ left [\ begin {matrix} 0 & 1 & 2 & 1 \\ 1 & 0 & 0 & 0 \\ 2 & 0 & 0 & 3 \\ 1 & 0 & 3 & 0 \ end {matrix} \ right]. \ end {align *} $ inline $

No caso de selos, nossa rede precisaria aprender a reconhecê-los por todas as permutações possíveis de linhas e colunas - esse é outro problema. Como exercício, tente alterar a numeração dos pontos na imagem abaixo para que, quando você os conecte em série, consiga um gato.

O próximo problema para gráficos com redes neurais comuns é a dimensão de entrada padrão. Quando trabalhamos com imagens, sempre normalizamos o tamanho da imagem para enviá-la à entrada da rede - é um tamanho fixo. Esses gráficos não funcionarão com gráficos - o número de vértices pode ser arbitrário - apertar a matriz de conectividade para uma determinada dimensão sem perder informações é outro desafio.

Solução - vamos construir novas arquiteturas, inspiradas na estrutura dos gráficos.

Para fazer isso, usamos uma estratégia simples de duas etapas:

1. Para cada vértice, construímos um gráfico computacional usando um tramp;
2. Coletamos e transformamos informações sobre vizinhos.

Lembre-se de que armazenamos as propriedades dos vértices em vetores$$ $ inline $ f ^ {(u)} $ inline $ - colunas matriciais$$ $ inline $ X \ in \ mathbb {R} ^ {k \ times | V |} $ inline $ e nossa tarefa é para cada vértice$$ $ inline $ u $ inline $ coletar propriedades de vértices vizinhos$$ $ inline $ f ^ {(v \ in N (u))} $ inline $ para obter vetores de incorporação$$ $ inline $ z_ {u} $ inline $ . Um gráfico computacional pode ter profundidade arbitrária. Considere uma opção de duas camadas.

A camada zero é as propriedades dos vértices, a primeira é uma agregação intermediária usando alguma função (indicada por um ponto de interrogação), a segunda é a agregação final, que produz os vetores de incorporação de interesse para nós.

E o que há nas caixas?

No caso simples , uma camada de neurônios e não linearidade:

$$$$ exibir $$ h ^ 0_v = x_v (= f ^ {(v)}); \\ h ^ k_v = \ sigma (W_k \ sum_ {u \ in N (v)} \ frac {h ^ {k-1} _v} {| N (v) |} + B_k h ^ {k-1} _v), \ forall k \ in \ {1, ..., K \}; \\ z_v = h ^ K_v, $$ display $$

onde$$ $ inline $ W_k $ inline $ e$$ $ inline $ B_k $ inline $ - os pesos do modelo que aprenderemos por descida gradiente, aplicando uma das funções de perda consideradas, e$$ $ inline $ \ sigma $ inline $ - não linearidade, por exemplo, RELU:$$ $ inline $ \ sigma (x) = máximo (0, x) $ inline $ .

E aqui nos encontramos em uma encruzilhada - dependendo da tarefa em mãos, podemos:

• estudar sem um professor e tirar proveito de qualquer uma das funções de perda consideradas anteriormente - vagabundos ou o peso das arestas. Os pesos resultantes serão otimizados para que vetores de vértices semelhantes sejam colocados compactamente;
• comece a treinar com um professor, por exemplo, para resolver o problema de classificação, imaginando se o medicamento será tóxico.

Para o problema de classificação binária, a função de perda assume a forma:

$$$$ display $$ L = \ sum_ {v \ in V} y_v log (\ sigma (z_v ^ T \ theta)) + (1-y_v) log (1- \ sigma (z_v ^ T \ theta)), $ $ display $$

onde$$ $ inline $ y_v $ inline $ - classe de vértice$$ $ inline $ v $ inline $ ,$$ $ inline $ \ theta $ inline $ É o vetor de pesos e$$ $ inline $ \ sigma $ inline $ - não linearidade, por exemplo um sigmóide:$$ $ inline $ \ sigma (x) = \ frac {1} {1 + e ^ {- x}} $ inline $ .

Aqui, um leitor treinado reconhecerá a entropia cruzada e a regressão logística, enquanto um leitor despreparado pensará em fazer um curso aberto de aprendizado de máquina para se sentir confortável com a tarefa de classificação , algoritmos simples e mais avançados para resolvê-lo (incluindo aumento de gradiente ).

E seguiremos em frente e consideraremos como o GraphSAGE , o prenúncio da Decagon, funciona.

Para cada vértice$$ $ inline $ v $ inline $ vamos agregar informações dos vizinhos$$ $ inline $ u \ in N (v) $ inline $ e ela mesma.

$$$$ display $$ h ^ k_v = \ sigma ([W_k \ cdot AGG (\ {h ^ {k-1} _u, \ forall u \ in N (v) \}), B_k h ^ {k-1} _v]), $$ display $$

onde$$ $ inline $ AGG $ inline $ - uma designação generalizada da função de agregação - o mais importante - diferenciável.

Média: calcule uma média ponderada dos vizinhos

$$$$ display $$ AGG = \ sum_ {u \ in N (v)} \ frac {h ^ {k-1} _u} {| N (v) |}. $$ display $$

Pooling: valor médio / máximo por elementos

$$$$ display $$ AGG = \ gama (\ {Qh ^ {k-1} _u, \ forall u \ in N (v) \}). $$ display $$

LSTM: Agite o ambiente (não misture!) E execute no LSTM

$$$$ display $$ AGG = LSTM ([h ^ {k-1} _u, \ forall u \ in \ pi (N (v))]). $$ display $$

Pinterest, , PinSAGE .

LSTM ( ). IT-.

:

• : , — , .
• , : / , — .

, — . , . , , , . (/) , , , — — , 30 .

.

— (multi-label node
classification task) — . — . () ( — — 42% ). GraphSAGE, , — .

!

, — , , . , .

- , Decagon. , -, -, , -, — ri . . - 964 ( ) .

— , -, -.

,

$$

$$h^k_v = \sigma(\sum_rW^{k-1}_r(\sum_{u \in N_r(v)} \frac{h^{k-1}_u}{\sqrt{|N_r(v)||N_r(u)|}}+\frac{h^{k-1}_v}{|N_r(v)|})),$$

onde $$$\sigma$— , RELU. , Decagon — . , , GraphSAGE. , .

, .

— , . -. $$$(u,r,v)$, :

$$$\begin{align*}g(u,r,v) = \left\{ \begin{matrix} z^T_uD_{r_i}RD_{r_i}z_j & u,v - ; \\ z^T_uM_rz_v & u,v - \, \, , \,\, \, . \end{matrix} \right.\end{align*}$

, :

$$

$$p^{uv}_{r} = p((u,r,v) \in E) = \sigma (g(u, r, v)), \sigma(x) = \frac{1}{1 + e^{-x}}.$$

, (end-to-end) -, : (i) $$$W_r$— , (ii) $$$M_r$— - -, (iii) $$$R$— , (iv) $$$D_{r_i}$— .

— - .

— .

— , , : 1) — — ; 2) " , , , " — - . , , , .

— — .

, ( ) , . , , GenBank 1 , , - — , . — , - ( ) , SNAP .

.

Neo4j , (property graph).

, . , , — (i) -, (ii) , (iii) , — — . .

— :

Além disso, a contribuição do Neo4j para o setor é criar a linguagem Cypher declarativa , que implementa um modelo de gráfico com propriedades e opera de forma semelhante ao SQL com os seguintes tipos de dados: vértices, relações, dicionários, listas, números inteiros, ponto flutuante e números binários, e cordas. Um exemplo de consulta que retorna uma lista de filmes com Nicole Kidman:

MATCH (nicole:Actor {name: 'Nicole Kidman'})-[:ACTED_IN]->(movie:Movie) WHERE movie.year < $yearParameter RETURN movie 

Usando muletas, o Neo4j pode ser feito para funcionar na memória.

Também vale a pena mencionar o Gephi - uma ferramenta conveniente para visualizar e exibir gráficos em um avião - a primeira ferramenta de análise de rede testada pessoalmente. Com um alongamento, podemos assumir que no Gephi é possível implementar um gráfico com as propriedades dos vértices e arestas, embora trabalhar com ele não seja muito conveniente e o conjunto de algoritmos para análise seja limitado. Isso não prejudica os méritos do pacote - para mim, ele está em primeiro lugar entre as ferramentas de visualização. Ao dominar o formato de armazenamento interno GEXF , você pode criar imagens impressionantes. Ela atrai a capacidade de exportar facilmente para a Web, bem como a capacidade de definir propriedades para vértices e arestas no tempo e obter animações complexas como resultado - ele criou as rotas para vendedores ambulantes a partir de dados de vendas. Tudo graças ao layout dos gráficos no mapa pelas coordenadas dos vértices - a parte padrão do pacote.

Agora, conduzo a maior parte da pesquisa analiticamente, faço desenhos no final.

Minha busca por ferramentas e métodos de processamento de dados em sistemas complexamente conectados continua. Há três anos, encontrei uma solução para trabalhar com gráficos multimodais. A biblioteca SNAP de Jure Leskovek é uma ferramenta que ele mesmo desenvolveu e já mediu muitas coisas. Eu uso o Snap.py - a versão para Python (proxy para funções SNAP implementadas em C ++) e um conjunto de cerca de trezentas operações disponíveis é suficiente para mim na maioria dos casos.

Recentemente, Marinka Zhitnik lançou o MAMBO - um conjunto de ferramentas (dentro do SNAP) para trabalhar com redes multimodais e um tutorial na forma de uma série de notebooks Jupyter com uma análise exemplar de mutações genéticas.

Por fim, existe o SAP HANA Graph - lá dentro do ML, SQL, OpenCypher - tudo o que seu coração deseja.

A favor do SAP HANA, o fato de que a escavação provavelmente resultará em dados de transação bem estruturados do ERP, enquanto os dados puros valem muito. Outra vantagem - ferramentas poderosas para encontrar sub-gráficos por determinados padrões - uma tarefa útil e difícil, cuja implementação em outros pacotes não atendeu e utilizou programas especializados . Uma licença gratuita para o desenvolvedor fornece um banco de dados de 1 GB - apenas o suficiente para jogar com redes grandes o suficiente. Uma chamada engraçada - um conjunto de algoritmos analíticos prontos para uso - é pequena, o PageRank precisará ser implementado de forma independente. Para fazer isso, você precisará dominar o GraphScript , uma nova linguagem de programação, mas isso é um pouco. Como o meu treinador de remo slalom disse, para o mestre - é poeira!

Agora, sobre onde obter os dados para criar gráficos a partir deles. Algumas idéias:

• Repositórios Públicos da Universidade: Stanford - General and Biomedical , Colorado ;
• Combine o plano do projeto com a estrutura organizacional e o registro de riscos;
• Identifique o relacionamento entre estrutura do produto, tecnologia e desejos do usuário;
• Realizar um estudo sociográfico em equipe;
• Crie algo de sua autoria, inspirado nos projetos do curso cs224w do ano passado .

O que temer

Podemos dizer que aqui será o último aviso sobre os riscos associados a esta parte.

Como sabem, senhoras e senhores, o objetivo do programa é refletir o estado das coisas na vanguarda de um grupo de pesquisa muito produtivo e generosamente financiado. É como Leningrado , apenas sobre matemática moderna. Possíveis efeitos colaterais:

1. Dunning-Krueger , modificado, sem a euforia de um novato e platô de excelência. Leskovek tenta recuperar o atraso.
2. Tédio em uma província à beira-mar. Das 400 pessoas no curso que receberam o aparato, elas me fizeram escrever um projeto e passar no exame na primeira sessão durante o meu segundo programa de mestrado, a contagem foi de um ano e meio. Os professores em suas atividades de pesquisa permaneceram no nível das medidas de modularidade e centralidade. Em mitaps sobre python e dados também é triste. Em geral, se você não sabe se divertir, eu avisei.
3. Orgulho em um sotaque eslavo no discurso em inglês.

Nota de reprodução

Olá reprodutor!

Na aventura que Jura Leskovek nos deu, você precisa de tempo livre. O curso consiste em 20 palestras, quatro trabalhos de casa, cada um dos quais é recomendado alocar cerca de 20 horas, literatura recomendada, bem como uma extensa lista de materiais adicionais que tornarão possível uma primeira impressão do estado das coisas na vanguarda do progresso em qualquer um dos tópicos discutidos.

Para concluir as tarefas, é altamente recomendável usar a biblioteca SNAP (em certo sentido, todo o curso pode ser considerado uma visão geral de seus recursos).

Além disso, você pode tentar implementar seu próprio projeto ou escrever um tutorial sobre o tópico que desejar.

Penso que após a imersão na teoria dos grafos, perguntas sobre árvores não serão mais assustadoras. No entanto, essa é apenas a opinião de um amador que nunca em sua vida assumiu a posição de desenvolvedor que não foi entrevistado.